はじめに
こんにちは,こんばんは,おはようございます.NTTドコモ先進技術研究所の田中です.第1回目の記事を合わせると3回目の登場です.
突然余談から入りますが,皆さんはちゃんと「サンプル数」と「サンプルサイズ」を使い分けていますか?本記事のタイトルを見て違和感を感じなかった人は,おそらくきちんと使い分けていない人だろうと思います.サンプル数は「何回標本抽出を行ったか(群の数とか)」を示す数で,サンプルサイズが「標本数 $n$ 」です.ちゃんと使い分けましょう.同じように「母数」も「分母」の意味で使っている人がいますが,これも違うので気をつけましょう.
さて,いきなり話が脱線してしまいましたが,今回はサンプルサイズが小さい場合の機械学習について取り上げたいと思います.サンプルサイズが小さい場合というのは,学習データ $\boldsymbol{x}_1, \dots, \boldsymbol{x}_n \in \mathbb{R}^d$ があったときに,単純に $n$ が小さい場合と
d > n \quad \textrm{or} \quad d>>n
が成り立つ,つまり高次元データを対象とする場合があると思います.
今回の記事では,高次元データを扱う際に注意すべき事に触れつつ,単純に $n$ が小さい場合に使える機械学習手法の例としてMETA-Learningの手法について紹介します.
高次元データを扱うときの注意
高次元データだと何が困るのか?
機械学習の理論は,基本的には数理統計学や多変量解析と呼ばれる分野で構築された理論を基に構築されていて,この辺の分野で伝統的に構築されてきた理論では,$d<n$ が前提となっています.すなわち,高次元データでは「機械学習のアルゴリズムで計算は出来たけど,それがどの程度『正しい』のかは保証できない」ということが起こります.
ちなみに,なぜ伝統的な数理統計学の世界で $d < n$ を前提とした理論が構築されてきたのかという話ですが,おそらく $d > n$ という仮定にニーズがなかったのでしょうね.実際,Hand, et al. (1993) で当時の有名データセットが紹介されていますが,殆どが10次元程度で $d < n$ を満たしています.
ところが,1990年代の後半になってから $d > n$ というデータが多く現れるようになり,2000年代になってから $d > n$ の枠組みでの高次元データの研究が徐々に進み始めたようです.
少し話が脱線しましたが,$d > n$での理論を構築するために何が難しいのかと言うと,
- 標本共分散行列の逆行列が存在しない or 不安定
- 固有値の推定が不安定
- 分布の検定が難しい
- なんか色々と直感に反したことが起こる(よく次元の呪いと呼ばれるアレ)
などがあります.
困ることの例:直感に反することが起きる例
$\boldsymbol{x} \sim \mathcal{N}_{d}(\boldsymbol{0}, \boldsymbol{I}_{d})$ であるとします.$d\to \infty$のとき
\left\| \boldsymbol{x} \right\| = \sqrt{d} + O_{p}(1)
が成り立ちます.確率オーダーを表す $O_p(1)$ が出てきていますが,これは直感的には「分布の裾がきちんと0に落ちている」という意味で,上式は「 $\boldsymbol{x}$ が半径 $\sqrt{d}$ の球面上に集まる」ということを意味しています(確率オーダーについての厳密な解説は最後におまけとして載せました).俗に言う球面集中現象です.1次元や2次元の場合からはなかなか想像しづらいですよね.
じゃあどうすれば良いのか?
高次元データに対して機械学習を適用していくには,以下のうような選択肢があると思います:
- 高次元のままでもうまく機能する機械学習の手法(カーネル法とか?)を作る
- 次元圧縮をする
- 特徴量選択をする
1つ目の選択肢は,割と数学が強い人でないと厳しい印象があります.僕のような数学弱者には厳しみが強いのでここではスキップします.
2つ目の選択肢に該当するものだと,データにPCAを適用して次元を圧縮するという方法が考えられます.しかし,これも気をつけなければいけない点があります.PCAは次元圧縮する手法にも関わらず,$d > n$ の設定だと次元の呪いを受けます.具体的にはPCAの計算に必要な標本固有値を推定する際に,通常の標本固有値の計算方法では,標本固有値が真の固有値よりも大きめに推定されてしまいます.ちなみに,この問題に関しては Yata, & Aoshima (2010a, 2010b, 2012, 2013) において高次元データでも機能するPCAの手法が提案されています.
3つ目の特徴選択に関しては,こちらのページ で詳しく解説されていて,高次元データに対する有効な特徴量選択の手法はあまり提案されていないようです.ただ,個人的には Yamada et al. (2018) で提案されているHSIC Lassoは著者の山田先生のページにPythonによる実装も置いてあって使いやすいと思います.
ただサンプルサイズが小さい場合
この場合は,実務で「今あるデータでやってみて」と言われているパターンか,データを取得するのがとても大変で,あまりデータが集まらないパターンのどちらかだと思います.前者に関して言いたいことはたくさんありますが,それは一旦おいておきましょう.
こういう場面に遭遇した時,有力な選択肢として Transfer LearningやFew-Shot Learning(もう少し広く言うとMETA-Learning)を使うことを考えるでしょう.今回は,ICLR2019に投稿されたMeta Learningの手法に関す論文「How to train your MAML」を紹介します.
論文の概要
メタ学習は,大量の様々なタスクを使って「どうやって学習するか」を学習する (例えば、モデルパラメータの初期値を学習する) 手法で,初めてみる新しいタスクに対してモデルがすぐに適応できるようになることを目指しています.典型的なメタ学習の方法には,教師あり学習・強化学習・遺伝的なアルゴリズムがあります.
教師ありメタ学習の手法の中でも,Model Agnostic Meta Learning (MAML) はシンプルな手法でありながら,SOTAを達成しています(多分).MAMLは,大雑把に言うと,サポートセットを使って学習し,ターゲットセットで精度がでるようにモデルパラメータの初期値を最適化します.MAMLについては,この記事 で非常に詳しく解説されています.
この論文ではMAMLの問題点を特定し解決することで,学習の安定化・汎化性能の向上・収束速度の向上を行います.著者らは,MAMLを改善した提案手法をMAML++と名付けています.
論文のContribution
- メタ学習 (outer-loop) のLossをinner-loop (サポートセットでの学習) の各ステップで計算したLossの重み付き和にすることで,メタ学習を安定化させる
- 勾配の微分の次数をアニーリングすることで汎化性能を上げる
- Batch Normalizationに移動統計を使うことで、汎化性能を上げる
- 学習のステップごとに異なるBatch Normalizationのbiasを用いることで,汎化性能を上げる
- 学習のステップごと、レイヤーごとに学習率と勾配方向をメタ学習させることで,汎化性能を上げる
- メタ学習の学習率をcosineアニーリングすることで,汎化性能を上げる
手法のコア
Multi-Step Loss Optimization(MSL)
オリジナルのMAMLでは,初期パラメータ $\boldsymbol{\theta} = \boldsymbol{\theta}_0$ は,inner-loopの更新が全て終わった後のモデルパラメータで計算したターゲットセットでのLossで最適化されます.この方法だと,Lossの勾配が減少したり発散せずに逆伝搬できる保証はなく,勾配消失・勾配発散の問題が起こり得ます.
一方で,提案手法のMSLでは,各inner-loopの更新後のモデルパラメータで計算したターゲットセットでのLossを重み付き平均したLossで最適化します.特に,各ステップのLossの重み付き平均には,アニーリングを用います.具体的には,メタ学習の初期段階では,各ステップのLossは等しい重みで寄与させますが,メタ学習の更新が進むにつれて最初の方のステップからの寄与を徐々に減少させ,最終的にはオリジナルのMAMLと同様の $N$ ステップ目だけのLossにします.アニーリングを使うことで,最終的なLossをオリジナルのMAMLのLossと一致させつつ,学習を安定化することができます.下図の左側が従来のMAML,右側がMAMLにMSLを追加した計算プロセスになります.
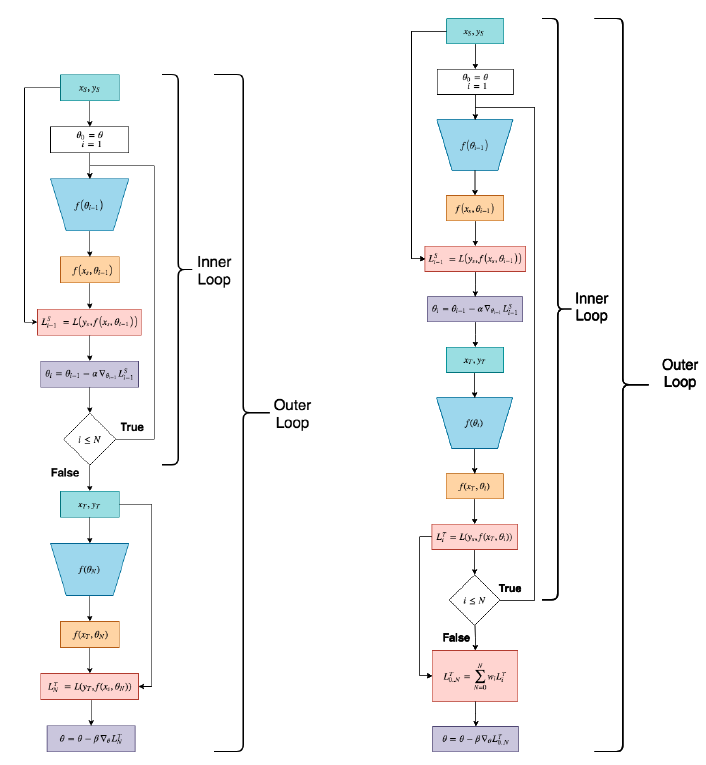
Derivative-Order Annealing
MAMLではouter-loopの最適化にinner-loopで最適化した結果が必要であり,これはHessian matrixを計算することに相当します.Hessian matrixの計算にはコストがかかるため,オリジナルのMAMLでは1次微分での近似も試していますが、近似により精度の悪化が起きています.そこで提案手法では,最初の50 epochは1次微分を用いることで高速化しつつ,それ以降は厳密な2次微分を使うことで汎化性能を担保します.2次微分を使った学習の前に1次微分を使った学習をすることは,事前学習のような役割を果たし,勾配消失・勾配発散の問題を避けることもできます.
Per-Step Batch Normalization Running Statistics
オリジナルのMAMLではbatchごとの統計量(平均と分散)のみをBatch Normalizationに使っています.この方法だと, Batch Normalizationのbiasは1つの平均と分散ではなく,様々な平均と分散に対応できなければならず,Batch Normalizationの有効性が下がります.提案手法では,inner-loopのステップごとに異なる移動統計量を集め,Batch Normalizationで使っています.
Per-Step Batch Normalization Weights and Biases
オリジナルのMAMLでは,各層ごとに単一のBatch Normalizationのbias $\beta$ を学習し,Batch Normalizationのweight $\gamma$ は固定の値にしています.これは,ネットワークの特徴量の分布が各ステップで似ていると仮定していることに相当します.しかしながら,inner-loopでモデルパラメータが更新されると特徴量の分布も変わるので,この仮定は一般には成り立ちません.提案手法では,inner-loopの更新ステップごとに異なるweight $\gamma$ とbias $\beta$ を学習します.そうすることで,inner-loopのステップごとの特徴量の分布に対して適切なweightとbaisが学習され,収束速度が上がり,学習が安定化し汎化性能が上がります.
Learning Per-Layer Per-Step Learning Rates and Gradient Directions
inner-loopの学習率や勾配方向は,モデルの収束性に大きな影響があります.MAMLの後続研究で,モデルパラメータごとに異なる学習率や勾配方向をメタ学習することで汎化性能が上がることが分かっています.しかし,メタ学習できるパラメータが増えて計算コストが高くなります.そこで提案手法では,同一レイヤーでは同じ学習率や勾配方向を学習させて,さらにinner-loopの各更新ステップごとに異なる学習率や勾配方向を学習させます.このようにモデルパラメータごとではなく,レイヤーごと,ステップごとの学習率を学習させることで必要なメモリが減り,計算コストを下げながら更新ステップごとの柔軟性をもたせることができます.
Cosine Annealing of Meta-Optimizer Learning Rate
オリジナルのMAMLではouter-loop(メタ学習)で固定の学習率を使っています.しかし他の研究では,学習率のアニーリングがモデルの汎化性能に寄与することが分かっています.そこで,提案手法ではメタ学習の学習率にcosineアニーリングを用います.それによって,学習率のハイパーパラメーター探索を行わずに高い精度を出すことが可能になります.メタ学習の学習率をアニーリングする事でメタ学習がより効果的に行なえ,結果として汎化性能が向上します.
実装
著者のgithub に実装が公開されているので省略.
おわりに
今回は高次元データを扱うときの注意点に触れた後,単純に「サンプルサイズが小さいのだが?」という問題への対策としてMeta Learningの一つであるMAML++について紹介しました.データ分析を仕事にしている方の多くは,「scikit-learn使ったらすべて解決!」のようなデータを分析するケースは多くないと思います.その中でも特に今回紹介したようなケースは対処が難しくなる場合も多く,特徴量エンジニアリングだけで乗り越えるのが難しい場合もあります.そんなときに,高次元データの統計学やFew-Shot Learning, Meta Learningに関する研究まで手を広げてサーベイしてもらえると,もしかしたらなにかヒントが得られるかもしれません.
おまけ:確率オーダーの定義
確率変数列 $\left\{ Z_n \right\}_{n\in \mathbb{N}}$ に対し,$Z_n = O_{p}(1)$ を以下で定義します:
\lim_{z\to \infty} \limsup_{n\to \infty} P(|Z_n| > z) = 0.
これは,厳密に書くと
\forall \varepsilon > 0, \exists \delta > 0 \quad \textrm{s.t.} \quad \forall z > \delta, \limsup_{n\to \infty} P(|Z_n| > z) < \varepsilon
となります.$\limsup_{n\to \infty} P(|Z_n| > z) = \inf_{n\in \mathbb{N}}\sup_{j\geq n} P(|Z_j| > z) $ であることから,上式は
\forall \varepsilon > 0, \exists \delta > 0 \quad \textrm{s.t.} \quad \forall z > \delta, \inf_{n\in \mathbb{N}} \sup_{j\geq n} P(|Z_j| > z)< \varepsilon
となり,$\sup_{j\geq n} P(|Z_j| > z)$ が単調減少数列であることから,
\begin{align*}
& \forall \varepsilon > 0, \exists \delta > 0 \quad \textrm{s.t.} \quad \forall z > \delta, \exists m\in \mathbb{N} \quad \textrm{s.t.}\quad \forall n \geq m, \sup_{j\geq n} P(|Z_j| > z)< \varepsilon \\
\Longleftrightarrow & \forall \varepsilon > 0, \exists \delta > 0 \quad \textrm{s.t.} \quad \forall z > \delta, \exists m\in \mathbb{N} \quad \textrm{s.t.}\quad \forall n \geq m, P(|Z_n| > z)< \varepsilon \\
\Longleftrightarrow & \forall \varepsilon > 0, \exists \delta > 0, \exists m\in \mathbb{N} \quad \textrm{s.t.} \quad \forall \forall n \geq m, P(|Z_n| > \delta)< \varepsilon \tag{1}
\end{align*}
となります.式 (1) は,ある $\delta$ 以上の領域では確率が $\varepsilon$ で抑えられる,つまり,分布の裾がちゃんと落ちているということを表しています.
参考文献
- Hand, D. J., Daly, F., McConway, K., Lunn, D., & Ostrowski, E. (1993). A handbook of small data sets. cRc Press.
- Yata, K., & Aoshima, M. (2010a). Effective PCA for high-dimension, low-sample-size data with singular value decomposition of cross data matrix. Journal of multivariate analysis, 101(9), 2060-2077.
- Yata, K., & Aoshima, M. (2010b). Intrinsic dimensionality estimation of high-dimension, low sample size data with d-asymptotics. Communications in Statistics—Theory and Methods, 39(8-9), 1511-1521.
- Yata, K., & Aoshima, M. (2012). Effective PCA for high-dimension, low-sample-size data with noise reduction via geometric representations. Journal of multivariate analysis, 105(1), 193-215.
- Yata, K., & Aoshima, M. (2013). PCA consistency for the power spiked model in high-dimensional settings. Journal of multivariate analysis, 122, 334-354.
- Yamada, M., Tang, J., Lugo-Martinez, J., Hodzic, E., Shrestha, R., Saha, A., ... & Radivojac, P. (2018). Ultra high-dimensional nonlinear feature selection for big biological data. IEEE Transactions on Knowledge and Data Engineering, 30(7), 1352-1365.