目次
1.はじめに
2.実装の動機
3.この記事で言いたいこと
4.技術編
5.実装編
6.おわりに
7.参考文献
8.忙しい人向けの手順共有
本記事は NTTドコモ R&D AdventCalendar2021 の12月14日の記事です。
1. はじめに
どうもNTTドコモ クロステック開発部の小松です。
普段の業務は再生可能エネルギーや電力を題材にした人間の行動に関するの研究・開発をしています。
本記事では遺伝的アルゴリズムの実用例をご紹介させていただきます。
遺伝的アルゴリズムは社内の研究開発に活用することを検討しておりまして、また、個人的にも気になっている手法です。
なお、今回ご紹介する実装は「音楽生成」で、完全な、興味・趣味への応用になります!
それでは、どうぞよろしくお願いします。
2. 実装の動機
今回アドベントカレンダーに臨むにあたって、「なぜ遺伝的アルゴリズムで、なぜメロディー生成なのかということについて説明します。
遺伝的アルゴリズム:業務への応用
新規のビジネスにつながる検討の段階でスケジュール最適化を検討していて、現状分かっている知識で、何か作りたいなと考えました。
メロディー生成①:DAWやDTMに興味があるから
「じゃあなんでメロディー生成なの?」と思われた方がいるかもしれません。
この点については、「pythonで音楽関係のデータ分析知見を深めつつ最終的に音楽を作成したい」というのが筆者として興味のある分野であり、実装としてはいい題材かなと思った次第です。
メロディー生成②:イベント的にぴったりの題材だから
アドベントカレンダーはヨーロッパでクリスマスまでの準備期間として定着しているようですが、
本記事でクリスマスソングを題材にすることで、皆さんにも「クリスマスがもうじきやってくる...!」という意識が高まればと思いました!
3. この記事で言いたいこと
以下を紹介します。
遺伝的アルゴリズムで実用的なものが作れる
特に**「遺伝的アルゴリズムって何ができるんだろう?」とか、「pythonで音楽生成したいけど、何から始めて良いやら....」という人にとって実装のきっかけづくり**となる部分を今回サポートできればと思います!
そこで本記事を通して実装に不安な方でも音楽生成ができることを目指します。
- 技術編
- 遺伝的アルゴリズムとは
- 実装の動機
- 実装編
- 実行環境
- 各ライブラリの説明(mido,deap)
- 下準備
- 実装
※技術編は概要程度に留めつつ(自分が説明するより、わかりやすい記事がたくさんあったというのもありますが...)、実装の部分のポイントをご紹介できればと思います!
実装のためにはある程度の問題設定は必要
なんとなく作ってみるというよりは、「どういったシナリオでこのプログラムが使えそうか」
ということをイメージながら実装することに意味があると思うので、想定シナリオを設定しました。
本記事では、下記のような条件のもとで、**「原曲とまるっきり同じメロディーを限定された情報の中で生成する」**という問題の解決を目指します。
ライブラリなどは充実してますが、構想段階から検討し実装することにはなるので、多少は現実的でないシナリオかもしれませんが、ご了承いただけますと幸いです。
想定シナリオ
- メロディー情報があるが、音楽制作初心者なので、音楽が作れない。(繋がりの良い音のコンビネーションもわからない)
- 曲の中で鍵盤を叩く回数は知っている。
- メロディーに活用する鍵盤番号、音の大きさの種類、長さの種類は知っている。
- 上記の頻度に関する情報はない。
- 作成したいものは単音のメロディーであり、単音同士のオーバーラップは発生してないものとする。(指1本で引くことができるメロディー)
- メロディー生成時の評価は元の音源との比較による要素の一致率を確認できるものとする。
- 鍵盤番号、音の大きさ、長さのそれぞれの羅列は独立して考えることができるものとする。
4. 技術編
遺伝的アルゴリズム
端的にいうと、生物の進化を参考に設計された近似解を求めるアルゴリズムです(Genetic Algorithm:GAともいいます。)。
その背景にはダーウィンの進化論があり、「生き物の進化は各種個体で子孫を残す際に、厳しい環境でも生存できるよう遺伝が生存し、場合によってはこれまでの親の遺伝子とは全く異なる情報を獲得することもある(突然変異)。」という自然淘汰の説に倣っています。
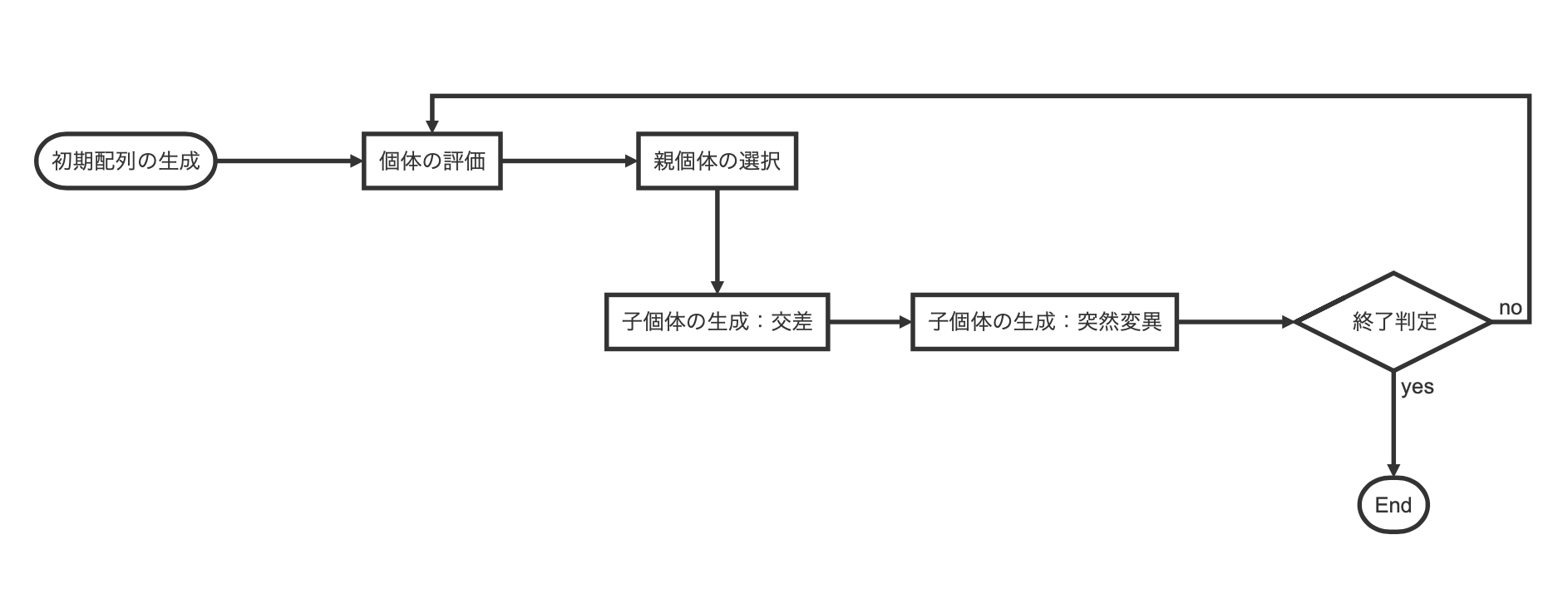
一般的なGAの設計としては次のようなステップを経て世代が更新されています。
初期配列の生成
例えば、[2,3,4,6,6,7,8,9,9,0]といった配列で構成されたものを指していて、遺伝子配列の長さや配列の要素を用途によって任意に設計可能です。ここで構成要素の位置や数値によってその個体が良い種別かどうかを判別する鍵となります。(列数で重要度が異なる、なども設計によっては可能と思います。)
評価
適応度という考え方があり、各遺伝子要素の適合度合いから採点し、その遺伝子がどれだけ優れているかを示す指標となっています。この適応度をもって各個体の評価を実施していきます。【実装では正しい要素か否かを1,0判定します】
選択
-
ルーレット選択
各個体数の適合度と総計から選択確率を作成する。そのため適合度の低い個体も選ばれる可能性があります。
個体iを選択する確率を$p_i$とすると、適合度$f$の総和(j=1~N)に対する$f_i$の割合から求められます。
$$
p_i=\frac{f_i}{\sum_{j=1}^{N}f_k}
$$ -
トーナメント選択【実装はこちらを採用】
N個の個体がその世代にいるとして、その中から M 個の個体をランダムに抽出し、適合度の最も高い個体を選択し続け、N個集まるまで、試行することなどを指します。
-
その他、エリート保存選択やランキング選択などがあります。
交叉
親同士の掛け合わせによって子孫となる子個体を生成することを指します。
-
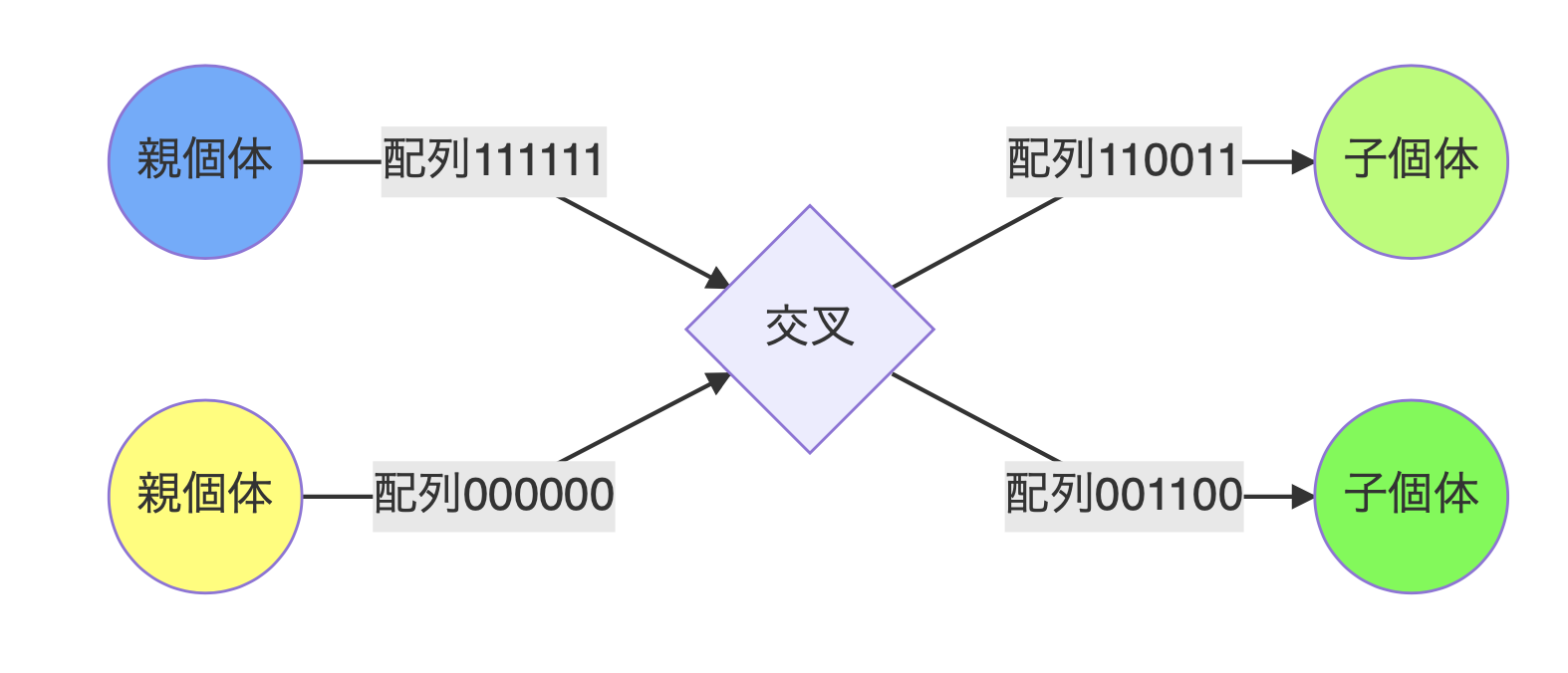
一点交叉
遺伝子1箇所に切れ目を入れて、その前後を交叉によってお互いに交換する方法です。
-
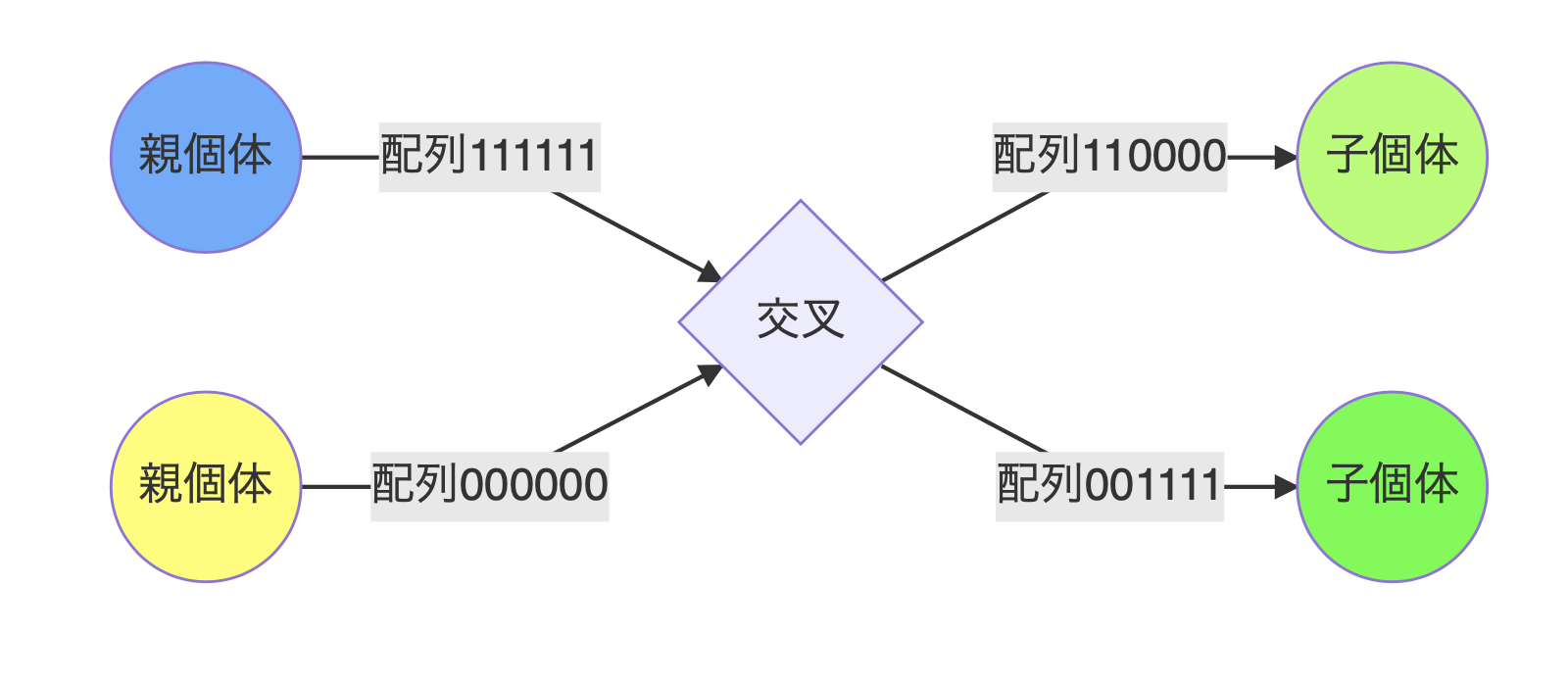
二点交叉【実装はこちらを採用】
遺伝子2箇所に切れ目を入れて、交叉によって交互に遺伝子を交換する方法です。
-
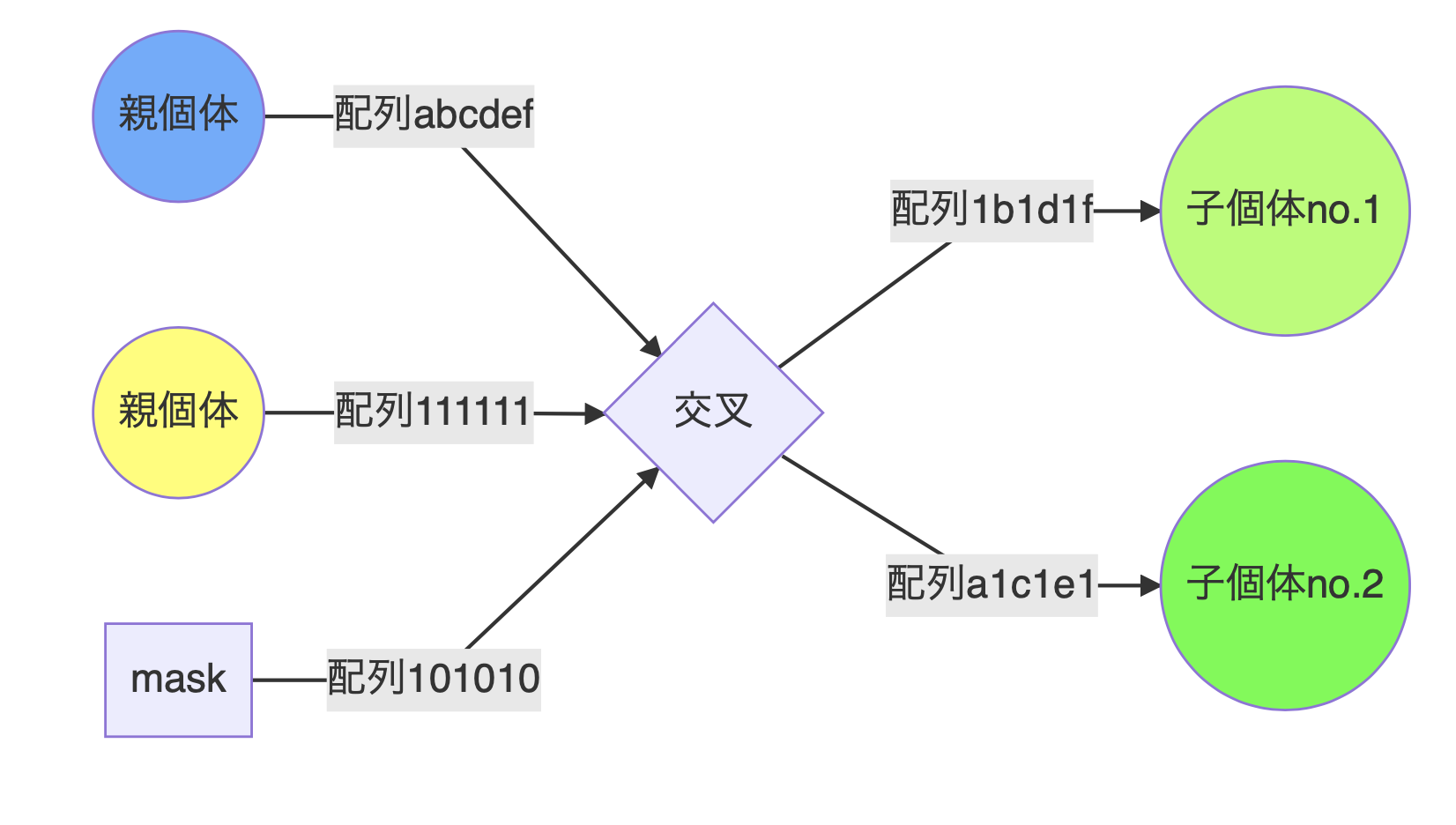
一様交叉
任意個の交差点をとることができる方法です。
まず0,1をランダムに生成します(マスクという)。
子個体no.1はマスクの0の位置でabc...の配列を持つ親の遺伝子を、1の位置で111...の配列を持つ親の遺伝子を引き継ぎ、子個体no.2はその逆の引き継ぎ方をさせます。
突然変異
ある確率で、遺伝子が入れ替わることです。その方法例は以下などによって再現されます。
- (値の反転)00000 -> 00001
- (値がランダムに置き換わる)12345 -> 92345
- (遺伝子同士の入れ替え)12345-> 15342【実装はこちらを採用】
終了判定
終了を判別する方法として今回は二点考慮しています。
- N回ループした際に終了
- 適合度がMの閾値を超えた時
5. 実装編
実行からメロディー再生までに必要なもの
今回は「メロディー生成をしたものを聞いてみるまで」を実際に体験されるのが良いと考えます。
そこで、お手元に無料の音楽制作ソフトやmidiファイルがあると良いでしょう。
その他基本的には、PCがあれば何不自由なく利用することができると思います。
- 音楽制作ソフト(Digital Audio Workstation:DAW)
- 例えば、GaragebandやCubase,cakewalkなどが挙げられます。
- midiファイル(今回は著作権フリーのmidiファイルを取得)
- Google colabratory
- mido, deapライブラリ
各ライブラリのご紹介
mido
ライブラリの公式ドキュメントはこちらから。公式ドキュメントの使用例を参考に今回のファイルを読み込んでみます。また、今回の検討ではファイルの読み込み、メロディーの挿入、書き出し機能を活用します。
ファイルの読み込み
from mido import MidiFile
# ファイルの読み込みを実施する。
mid = MidiFile('/content/drive/MyDrive/morobito2.mid')
# 読み込んだファイルの中身を閲覧する。このとき何行目に何があるか確認もできるようにした。
for i, track in enumerate(mid.tracks):
print('Track {}: {}'.format(i, track.name))
j=0
for msg in track:
print(msg,'----'j)
j+=1
実行結果からTrack3にメロディーベースとなるchurch orgの音源があることを確認しました。
また、この実行結果から、トラック情報を構成するものとして、
トラック=トラック名+MetaMessage(トラックで使用する楽器、出力時の設定、bpm設定)+message(どの音をどの期間出すか、ボリュームやパン、ペダルなどを踏むかどうかなど)
で構成されていることが確認できました。また、一音に対してnote_on,note_offについては一対になっていることも確認できます。
Track 0: l񬊎
MetaMessage('track_name', name='\x8f\x94\x90l\x82±\x82¼\x82è\x82Ä ', time=0)
MetaMessage('time_signature', numerator=2, denominator=4, clocks_per_click=24, notated_32nd_notes_per_beat=8, time=0)
MetaMessage('set_tempo', tempo=705882, time=0)
MetaMessage('set_tempo', tempo=731707, time=39840)
(中略)
Track 3: Church Org
MetaMessage('track_name', name='Church Org ', time=0)
MetaMessage('sequencer_specific', data=(67, 0, 1, 0), time=0)
MetaMessage('midi_port', port=0, time=0)
control_change channel=0 control=0 value=0 time=0
control_change channel=0 control=32 value=0 time=10
program_change channel=0 program=19 time=10
(中略)
note_on channel=0 note=74 velocity=100 time=4690
note_off channel=0 note=74 velocity=64 time=460
(中略)
メロディー作成、ファイルの書き出し
公式ドキュメントのスクリプトを参考にした掲載にはなりますが、下記のようにメロディーを生成し、midiファイルを出力するために必要なスクリプトになります。
from mido import Message, MidiFile, MidiTrack
# Midiflileに相当する関数
mid = MidiFile()
# 楽曲の中のトラックに相当する関数
track = MidiTrack()
# 楽曲の中のトラックをmidiファイルに結合
mid.tracks.append(track)
# bpm設定
track.append(MetaMessage('set_tempo', tempo=mido.bpm2tempo(120)))
# メロディーの1要素を格納する
track.append(Message('note_on', note=64, velocity=64, time=32))
track.append(Message('note_off', note=64, velocity=127, time=32))
# midiファイルとして書き出す
mid.save('new_song.mid')
なお、メロディーを構成する要素としては下記の通りです。
note_on: 鍵盤を押したことを表す
note_off: 鍵盤を話したことを表す
channel:どのチャンネルの音を出すか【検討外】
note: どの鍵盤番号に対する処理か
velocity:鍵盤を叩く強さを表す
time: note_on,note_off の時間差で鍵盤の押している長さを定義する認識。
DEAP
ライブラリの公式ドキュメントはこちらから。
今回はDEAPの中のOneMax問題のスクリプトを用いて、実装を行います。
OneMax問題は0,1で構成される配列(たとえば[0,1,1,0]など)の配列要素を全て1にする問題設定になります。
メソッド一つ一つの解説についてはまたどこかの機会でご紹介できればと思いますが、
後述の実装の中で、何を使っているか簡単にコメントアウトさせていただきます。
全体の流れ
今回下記のように実装を進めました。
- 下準備
- 遺伝的アルゴリズムによるメロディー生成の実装
- 出力の書き込み
下準備
-
お好きな音源(.midとファイル)をダウンロードして手元にご用意ください。
-
音楽編集を実施して、2音のメロディーを単音に変更しました。(Cubase11を使用、該当の音を選択削除)
-
ご自身で挑戦される場合はcakewalkなどの音楽制作ソフトをインストールした方がいいと思います。
-
一つの配列に2つの情報が入らないようにするための処置として、低音の鍵盤パートを削除しました。
-
morobito2としてmidiファイルを保存しています。
-
-
さらに簡易化のため若干の音源編集をします。(python上で,音の大きさや押下時間を調整します)
- ここではトラック3のメインとなるメロディーラインのデータを編集しています。(テンポと初期の余韻、末尾の余韻について調整を実施しています。)
import mido
from mido import Message,MidiFile,MidiTrack,MetaMessage
from mido import MidiFile
mid = MidiFile('/content/drive/MyDrive/morobito2.mid')
# あたらしくMidiファイルの格納先を作成
test_midi=MidiFile()
test_track=MidiTrack()
test_midi.tracks.append(test_track)
# bpmの設定
test_track.append(MetaMessage('set_tempo', tempo=mido.bpm2tempo(120)))
ty_l=['note_on']
no_l=[74]
vel_l=[100]
ti_l=[0]
# 初期値の調整
test_track.append(Message('note_on', channel=0, note=74, velocity=100, time=0))
# 強引ですが、track3の"note_on"と"note_off"のみを抽出し、その鍵盤番号と強さ、時間のデータを抽出
for i in mid.tracks[3][16:262]:
if i.type!='control_change':
test_track.append(i)
ty_l.append(i.type)
no_l.append(i.note)
vel_l.append(i.velocity)
ti_l.append(i.time)
ty_l.append('note_off')
# 末尾の調整
no_l.append(67)
vel_l.append(64)
ti_l.append(100)
test_track.append(Message('note_off', channel=0, note=67, velocity=64, time=100))
test_midi.save('/content/drive/MyDrive/test_midi.mid')
-
ユニークな値を抽出するために、データフレームを作成
- 「メロディーに活用する鍵盤番号、音の大きさの種類、長さの種類は知っている。」というシナリオになぞっています。
- 今回、検討箇所を簡易化するためにnote_onのtimeを20に一意に変更するようにしました。
- このとき、'note_on'では時間が20で、'note_off'は強さが一意に決定することを確認できるようにしています。
import matplotlib.pyplot as plt import pandas as pd #先ほど抽出したデータをデータフレーム化する df=pd.DataFrame(data=[ty_l,no_l,vel_l,ti_l]) df=df.T df[4]=1 #鍵盤番号や時間、強さの出現回数について可視化 print('pitch_unique') print(pd.crosstab([df[0],df[1]], df[4])) print('time_unique') print(pd.crosstab([df[0],df[3]], df[4])) print('velocity_unique') print(pd.crosstab([df[0],df[2]], df[4])) #データの傾向を確認することで、下記のように修正を実施 df.loc[df[0] == 'note_on', 3] = 20 #修正後の結果を表示 print('pitch_unique') print(pd.crosstab([df[0],df[1]], df[4])) print('time_unique') print(pd.crosstab([df[0],df[3]], df[4])) print('velocity_unique') print(pd.crosstab([df[0],df[2]], df[4])) -
正解ファイルの鍵盤番号と強さ、時間を抽出する
- 今回生成したメロディーを評価するための正解となる配列を作成します。
#遺伝的アルゴリズムで評価する際に活用する、正解となる配列を作成 True_note=df[df[0]=='note_on'][1].values True_time=df[df[0]=='note_off'][3].values True_velocity=df[df[0]=='note_on'][2].values
実装
実装コード
ここからは実際に、GAによってメロディー生成するまでの流れをご紹介します。まずは前工程で作成した、正解となるメロディー情報の羅列から、候補となるユニークな要素のみで構成された配列を作成します。これが選択可能な遺伝子の種類となります。
# 候補となる鍵盤番号
u_n=list(dict.fromkeys(True_note))
# 候補となる時間
u_t=list(dict.fromkeys(True_time))
# 候補となる強さ
u_v=list(dict.fromkeys(True_time))
deapのガイドブック上にあるサンプルプログラムを活用し、今回の問題である、正しいメロディーの自動生成のタスクへ応用します。(今回は、例として鍵盤番号配列の自動生成を実施した際のプログラムを紹介します。)
import random
import numpy as np
from deap import base
from deap import creator
from deap import tools
# 今回もサンプルスクリプト通り、値を最大化することに価値があるように適応度を生成
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)
toolbox = base.Toolbox()
# 候補となる鍵盤番号
u_n=list(dict.fromkeys(True_note))
# 候補となる時間
u_t=list(dict.fromkeys(True_time))
# 候補となる強さ
u_v=list(dict.fromkeys(True_velocity))
# 遺伝子の長さ
N=len(True_time)
# 正しい遺伝子(正解の配列)
True_gene=True_note
# 配列作成時にrandom_choiceによって、決まった値のみを遺伝子に格納するよう設定
# u_nの部分をu_v,u_tに変更することで変更可能
toolbox.register("attr_bool", random.choice, u_n)
# 個体の遺伝子長さを決定し、配列を作成する。
toolbox.register("individual", tools.initRepeat, creator.Individual,
toolbox.attr_bool, N)
# 1世代の個体数を定義
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# どれだけ配列が正しいかをここで定義している。
# 個体の持つ配列と正解の配列の各要素が一致する場合は1で活性化し、
# 反対は0で非活性になる配列自身の和をとることで、01最大化問題に落とし込む
def evalOneMax(individual):
rate=(1*(np.array(True_gene)==(np.array(individual))))
return sum(rate),
# ----------
# Operator registration
# ----------
# ゴールとなる適応度の設定
toolbox.register("evaluate", evalOneMax)
# 交叉する方法として、二点交叉を実施
toolbox.register("mate", tools.cxTwoPoint)
# 遺伝子を突然変異させる際に、任意の配列をシャッフルする
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
# 選択方法として、トーナメント方式を採用
toolbox.register("select", tools.selTournament, tournsize=3)
# ----------
def main():
random.seed(64)
# 1世代の生成によって300個の個体を作成
pop = toolbox.population(n=300)
# CXPB は二点交叉する場所を選択する確率
#
# MUTPB 変異確立
CXPB, MUTPB = 0.5, 0.2
#実行開始
print("Start of evolution")
# 親の世代の評価を実施する
fitnesses = list(map(toolbox.evaluate, pop))
# 結果を格納する配列の初期値を作成
m_l=[]
std_l=[]
max_l=[]
# 世代の評価を実施し、どのくらいの数評価したかを返す
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(pop))
# 全ての評価結果を返す配列を作成
fits = [ind.fitness.values[0] for ind in pop]
# 世代カウント
g = 0
# 進化をやめるまでの終了判定
while max(fits) < len(True_note) and g < 1000:
# 子の世代
g = g + 1
print("-- Generation %i --" % g)
# 子の選択
offspring = toolbox.select(pop, len(pop))
# 選択された子を配列化
offspring = list(map(toolbox.clone, offspring))
# 二点交叉を実施する
for child1, child2 in zip(offspring[::2], offspring[1::2]):
if random.random() < CXPB:
toolbox.mate(child1, child2)
# 適合度を計測
del child1.fitness.values
del child2.fitness.values
# 任意確率で子を突然変異させる
for mutant in offspring:
if random.random() < MUTPB:
toolbox.mutate(mutant)
del mutant.fitness.values
# 子の世代の適合度計算?
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
#子の世代の適合度
print(" Evaluated %i individuals" % len(invalid_ind))
# 次世代に受け渡すために値変更
pop[:] = offspring
# 適合度を格納
fits = [ind.fitness.values[0] for ind in pop]
length = len(pop)
mean = sum(fits) / length
sum2 = sum(x*x for x in fits)
std = abs(sum2 / length - mean**2)**0.5
print(" Min %s" % min(fits))
print(" Max %s" % max(fits))
max_l.append(max(fits))
print(" Avg %s" % mean)
m_l.append(mean)
print(" Std %s" % std)
std_l.append(std)
print("-- End of (successful) evolution --")
best_ind = tools.selBest(pop, 1)[0]
print("Best individual is %s, %s" % (best_ind, best_ind.fitness.values))
return max_l,m_l,std_l,best_ind,best_ind.fitness.values
if __name__ == "__main__":
n_m_l=[]
n_std_l=[]
n_max_l=[]
n_max_l,n_m_l,n_std_l,n_best_ind,n_best_ind.fitness.values=main()
結果の共有
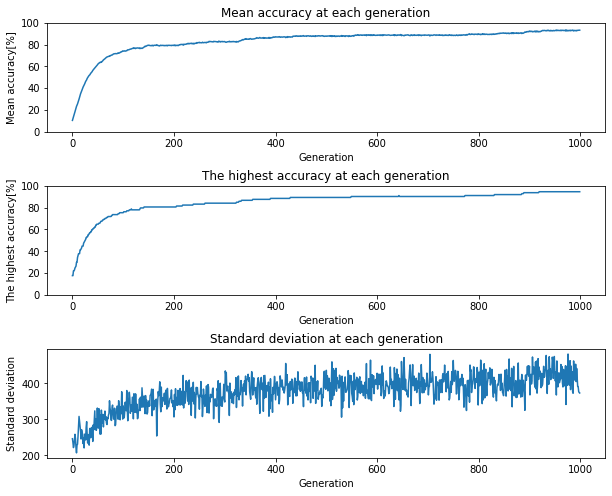
鍵盤番号に関する精度の可視化
原曲に100%等しいメロディーにはならず、もう少し突然変異の確率や、交叉の確率、選定方法を検討する必要がありそうです。
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
# 余白を設定
plt.subplots_adjust(hspace=0.5)
plt.subplot(3,1,1)
plt.plot(100*np.array(n_m_l)/len(True_note))
plt.title('Mean accuracy at each generation')
plt.ylabel('Mean accuracy[%]')
plt.xlabel('Generation')
plt.ylim(0,100)
plt.subplot(3,1,2)
plt.plot(100*np.array(n_max_l)/len(True_note))
plt.title('The highest accuracy at each generation')
plt.ylabel('The highest accuracy[%]')
plt.xlabel('Generation')
plt.ylim(0,100)
plt.subplot(3,1,3)
plt.plot(100*np.array(n_std_l))
plt.title('Standard deviation at each generation')
plt.ylabel('Standard deviation')
plt.xlabel('Generation')
plt.show()
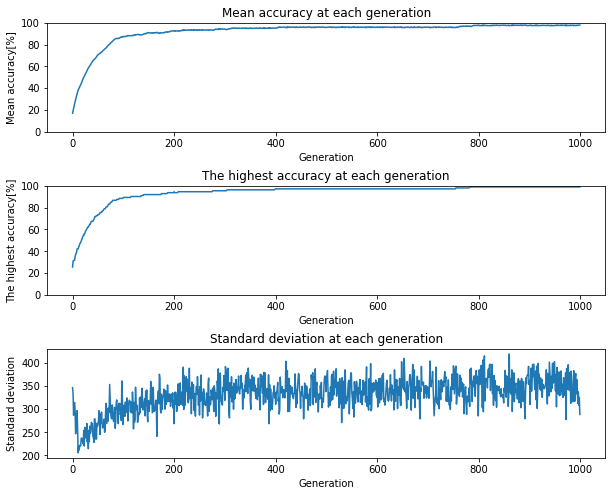
時間に関する精度の可視化(プログラム省略)
単音を出し続ける時間の導出は800世代の段階である程度高い精度が出る世代となり、ほとんど原曲と変わらないメロディー情報になりました。
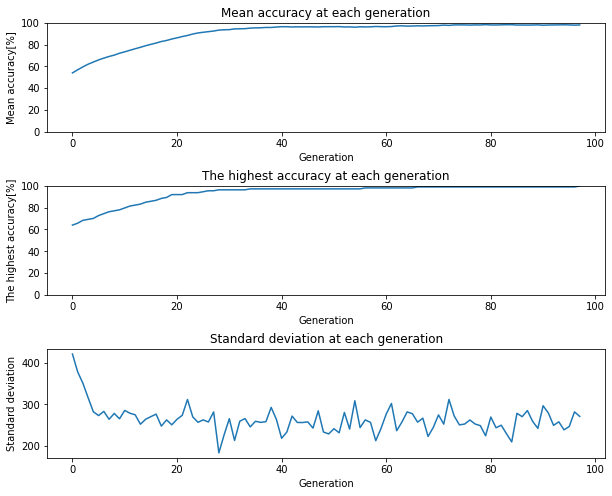
鍵盤を叩く強さに関する精度の可視化(プログラム省略)
鍵盤を叩く強さは、入力要素の種類数が鍵盤番号や時間と比較して少ないことから、短い世代で正しいメロディー情報を保存することがでたと考えます。
音楽データ(GA_midi.mid)の作成
ともあれ、完成した音楽データに必要な情報(pitch、time、velocityに相当するもの)の配列をそれぞれ活用して、midiデータを作成します。
import mido
from mido import Message,MidiFile,MidiTrack,MetaMessage
GA_midi=MidiFile()
GA_track=MidiTrack()
GA_midi.tracks.append(GA_track)
GA_track.append(MetaMessage('set_tempo', tempo=mido.bpm2tempo(120)))
for i in range(len(t_best_ind)):
GA_track.append(Message('note_on', channel=0, note=n_best_ind[i], velocity=v_best_ind[i], time=20))
GA_track.append(Message('note_off', channel=0, note=n_best_ind[i], velocity=64, time=t_best_ind[i]))
GA_midi.save('/content/drive/MyDrive/GA_midi.mid')
サウンドクラウドという音楽共有サイトに.wavに変換した結果を投稿したので、ご興味のある人は是非、試聴していただけると幸いです!
途中で音を外した際の違和感が際立って面白かったのでジャンルは「コメディ」で登録しました。
実装結果について考えると、鍵盤番号や音を出す時間について少しでも間違えていると、
音楽としてもかなり致命的なのがとても勉強になりました。笑
6. おわりに
GAの学習が終わった際のスコアだけを見ると、「完コピではないにしても、まあ違和感ないだろう」と思いましたが、結果として得られた出力としては、急に音が外れてていたりして、笑っちゃいました。
アドベントカレンダーの趣旨としては「クリスマスまでの準備期間」だと思いますので、この部分の精度の向上だったり、より厳しい問題設定の検討(例えば正解が何か全くわからず人間の判断に委ねるしかないような場合にどうすればいいか?)の勉強に時間を費やしてみたいと思います。
以上です、皆さんも良いクリスマスを過ごせると良いですね!
7. 参考文献
- mido 公式ドキュメント
- DEAP 公式ドキュメント
- フリーMIDI
- 遺伝的アルゴリズム
- ソフトコンピューティング演習 第5回
- Soundcloud
8. 忙しい人向けの手順共有
以下は、「とにかく動くものが欲しい」という人向けに手順を示します。
-
メロディーが単音のmidiファイルを準備
-
下記スクリプト実行
import mido from mido import Message,MidiFile,MidiTrack,MetaMessage from mido import MidiFile import pandas as pd #メロディーの該当するトラック番号Tn Tn=3 #ファイル読み込み #ファイルパスの指定をここでお願いします mid = MidiFile() #あたらしくMidiファイルの格納先を作成 test_midi=MidiFile() test_track=MidiTrack() test_midi.tracks.append(test_track) #bpmの設定 test_track.append(MetaMessage('set_tempo', tempo=mido.bpm2tempo(120))) #初期値の調整 ty_l=[] no_l=[] vel_l=[] ti_l=[] # 任意trackの"note_on"と"note_off"のみを抽出し、その鍵盤番号と強さ、時間のデータを抽出 for i in mid.tracks[Tn]: if (i.type=='note_on')or(i.type=='note_off'): test_track.append(i) ty_l.append(i.type) no_l.append(i.note) vel_l.append(i.velocity) ti_l.append(i.time) #正解となるメロディーデータを保存 test_midi.save('/content/drive/MyDrive/test_midi.mid') #正解となる配列をデータフレーム化 df=pd.DataFrame(data=[ty_l,no_l,vel_l,ti_l]) df=df.T df[4]=1 # 正解配列の作成 # 鍵盤番号は対になっているためnote_onのみの読み込み True_note=df[df[0]=='note_on'][1].values True_time_1=df[df[0]=='note_on'][3].values True_time_2=df[df[0]=='note_off'][3].values True_velocity_1=df[df[0]=='note_on'][2].values True_velocity_2=df[df[0]=='note_off'][2].values -
遺伝的アルゴリズムによってメロディー生成
実装プログラムが長いので折りたたみました。
import random
import numpy as np
from deap import base
from deap import creator
from deap import tools
#候補となる鍵盤番号生成
u_n=list(dict.fromkeys(True_note))
#候補となる時間生成
u_t_1=list(dict.fromkeys(True_time_1))
u_t_2=list(dict.fromkeys(True_time_2))
#候補となる強さ設定
u_v_1=list(dict.fromkeys(True_velocity_1))
u_v_2=list(dict.fromkeys(True_velocity_2))
#値を最大化することに価値があるように適応度を生成
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)
toolbox = base.Toolbox()
#遺伝子の長さ
N=len(True_note)
#正しい遺伝子(正解の配列)
True_gene=True_note
#遺伝子のとりうるパターン
factor=u_n
# 配列作成時にrandom_choiceによって、決まった値のみを遺伝子に格納するよう設定
toolbox.register("attr_bool", random.choice, factor)
# 個体の遺伝子長さを決定し、配列を作成する。
toolbox.register("individual", tools.initRepeat, creator.Individual,
toolbox.attr_bool, N)
# 1世代の人口を定義
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# どれだけ配列が正しいかをここで定義している。
# 個体の持つ配列と正解の配列の各要素が一致する場合は1で活性化し、
# 反対は0で非活性になる配列自身の和をとることで、01最大化問題に落とし込む
def evalOneMax(individual):
rate=(1*(np.array(True_gene)==(np.array(individual))))
return sum(rate),
#----------
# Operator registration
#----------
# ゴールとなる適応度の設定
toolbox.register("evaluate", evalOneMax)
# 交叉する方法として、二点交叉を実施
toolbox.register("mate", tools.cxTwoPoint)
# 遺伝子を突然変異させる際に、任意の配列をシャッフルする
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
# 選択方法として、トーナメント方式を採用
toolbox.register("select", tools.selTournament, tournsize=3)
#----------
def main():
random.seed(64)
# 1世代の生成によって300個の個体を作成
pop = toolbox.population(n=300)
# CXPB は二点交叉する場所を選択する確率
#
# MUTPB 変異確立
CXPB, MUTPB = 0.5, 0.2
#実行開始
print("Start of evolution")
# 親の世代の評価を実施する
fitnesses = list(map(toolbox.evaluate, pop))
# 結果を格納する配列の初期値を作成
m_l=[]
std_l=[]
max_l=[]
# 世代の評価を実施し、どのくらいの数評価したかを返す
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(pop))
# 全ての評価結果を返す配列を作成
fits = [ind.fitness.values[0] for ind in pop]
# 世代カウント
g = 0
# 進化をやめるまでの終了判定
while max(fits) < len(True_note) and g < 1000:
# 子の世代
g = g + 1
print("-- Generation %i --" % g)
# この選択
offspring = toolbox.select(pop, len(pop))
# 選択されたものをコピー
offspring = list(map(toolbox.clone, offspring))
# 二点交叉を実施する
for child1, child2 in zip(offspring[::2], offspring[1::2]):
# cross two individuals with probability CXPB
if random.random() < CXPB:
toolbox.mate(child1, child2)
# 適合度を計測
del child1.fitness.values
del child2.fitness.values
for mutant in offspring:
# 突然変異のプログラム
if random.random() < MUTPB:
toolbox.mutate(mutant)
del mutant.fitness.values
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
#子の世代の適合度計算
print(" Evaluated %i individuals" % len(invalid_ind))
# 子孫の世代の個体数に変更
pop[:] = offspring
# 適合度を格納
fits = [ind.fitness.values[0] for ind in pop]
length = len(pop)
mean = sum(fits) / length
sum2 = sum(x*x for x in fits)
std = abs(sum2 / length - mean**2)**0.5
print(" Min %s" % min(fits))
print(" Max %s" % max(fits))
max_l.append(max(fits))
print(" Avg %s" % mean)
m_l.append(mean)
print(" Std %s" % std)
std_l.append(std)
print("-- End of (successful) evolution --")
best_ind = tools.selBest(pop, 1)[0]
print("Best individual is %s, %s" % (best_ind, best_ind.fitness.values))
return max_l,m_l,std_l,best_ind,best_ind.fitness.values
if __name__ == "__main__":
n_m_l=[]
n_std_l=[]
n_max_l=[]
n_max_l,n_m_l,n_std_l,n_best_ind,n_best_ind.fitness.values=main()
#遺伝子の長さ
N=len()#()の内部にTrue_note,True_time_1~2,True_velocity_1~2を記入
#正しい遺伝子(正解の配列)
True_gene= #True_note,True_time_1~2,True_velocity_1~2を記入
#遺伝子のとりうるパターン
factor= #u_n,u_t_1~2,u_v_1~2を記入
if __name__ == "__main__":
n_m_l=[]
n_std_l=[]
n_max_l=[]
#n_best_ind,n_best_indの部分をu_n,u_t_1~2,u_v_1~2で生成するごと違う命名で配列を定義すること
n_max_l,n_m_l,n_std_l,n_best_ind,n_best_ind.fitness.values=main()
-
生成したリストでメロディー作成
import mido from mido import Message,MidiFile,MidiTrack,MetaMessage GA_midi=MidiFile() GA_track=MidiTrack() GA_midi.tracks.append(GA_track) GA_track.append(MetaMessage('set_tempo', tempo=mido.bpm2tempo(120))) #note_on,note_offでtime、velocityがバラバラの場合はGAをそれぞれ回して作成し、代入する for i in range(len(t_best_ind)): GA_track.append(Message('note_on', channel=0, note=n_best_ind[i], velocity=v_1_best_ind[i], time=t_1_bens_ind[i])) GA_track.append(Message('note_off', channel=0, note=n_best_ind[i], velocity=v_2_best_ind[i], time=t_2_best_ind[i])) GA_midi.save('/content/drive/MyDrive/GA_midi.mid') -
音楽編集ソフトで音楽を聴いてみる!