この記事は,数値計算 Advent Calendar 2022 13日目の記事です.この記事では,有限要素法で,ヘリウム原子に対するHartree-Fock方程式を解いてみる(Juliaでやってみた)の記事のコードを,GPUで高速化することを考えます.このコードの律速は,一般化固有値問題を解いている箇所
# 一般化固有値問題を解く
eigenval, phi = eigen!(hfem_val.hg, hfem_val.ug)
の一行のみであり,この一行の部分に総計算時間の約95%が集中しています.従って,この部分をGPUに任せることで,高速化が期待できます.この部分をGPUに任せるには,上記のコードを以下のように変更します.
# 一時配列の生成
tmpA = zeros(hfem_param.ELE_TOTAL, hfem_param.ELE_TOTAL)
tmpB = zeros(hfem_param.ELE_TOTAL, hfem_param.ELE_TOTAL)
# 一時配列にデータをコピー
copy!(tmpA, hfem_val.hg)
copy!(tmpB, hfem_val.ug)
# ホストメモリからデバイスメモリへデータコピー
A = CuArray(tmpA)
B = CuArray(tmpB)
# 一般化固有値問題を解く
d_W, d_VA = CUSOLVER.sygvd!(1, 'V', 'L', A, B)
# デバイスメモリからホストメモリへデータコピー
h_W = collect(d_W)
h_VA = collect(d_VA)
となります.なお,CUDA.jlを使用するため,using CUDAが必要です.これだけで,一般化固有値問題がGPUで解けます.簡単ですね.
プログラムの実行時間を,CPUのみ,CPU+GPUの二通りで比較したもの(及び高速化の比率)を以下に表で示します.なお,パフォーマンスを測定した環境は,
- CPU: Intel Core i9-10980XE (Cascade Lake-X, Hyper Threading ON (物理18コア論理36コア), Enhanced Intel SpeedStep Technology OFF, Turbo Mode OFF)
- メモリ: DDR4-3200 32GB (8GB×4)
- GPU: GeForce RTX 3080 10GB (8704 CUDAコア)
- OS: Linux Mint 21 "Vanessa"
- Juliaのバージョン: v1.8.3
であり,CPUのみとCPU+GPUの双方とも,3回計測し平均を取りました(カットオフ$ r_c = 50.0(a.u.) $,$ \left\vert E_{new}-E_{old}\right\vert $の閾値$ 5 \times 10^{-12} $).分割数は100~10000で計測しました.
| 分割数 | CPU(秒) | CPU+GPU(秒) | 高速化の比率(倍) |
|---|---|---|---|
| 100 | 0.4851 | 3.234 | 0.150 |
| 500 | 2.014 | 3.842 | 0.524 |
| 1000 | 7.264 | 5.390 | 1.348 |
| 5000 | 263.4 | 84.77 | 3.107 |
| 10000 | 2536 | 496.5 | 5.108 |
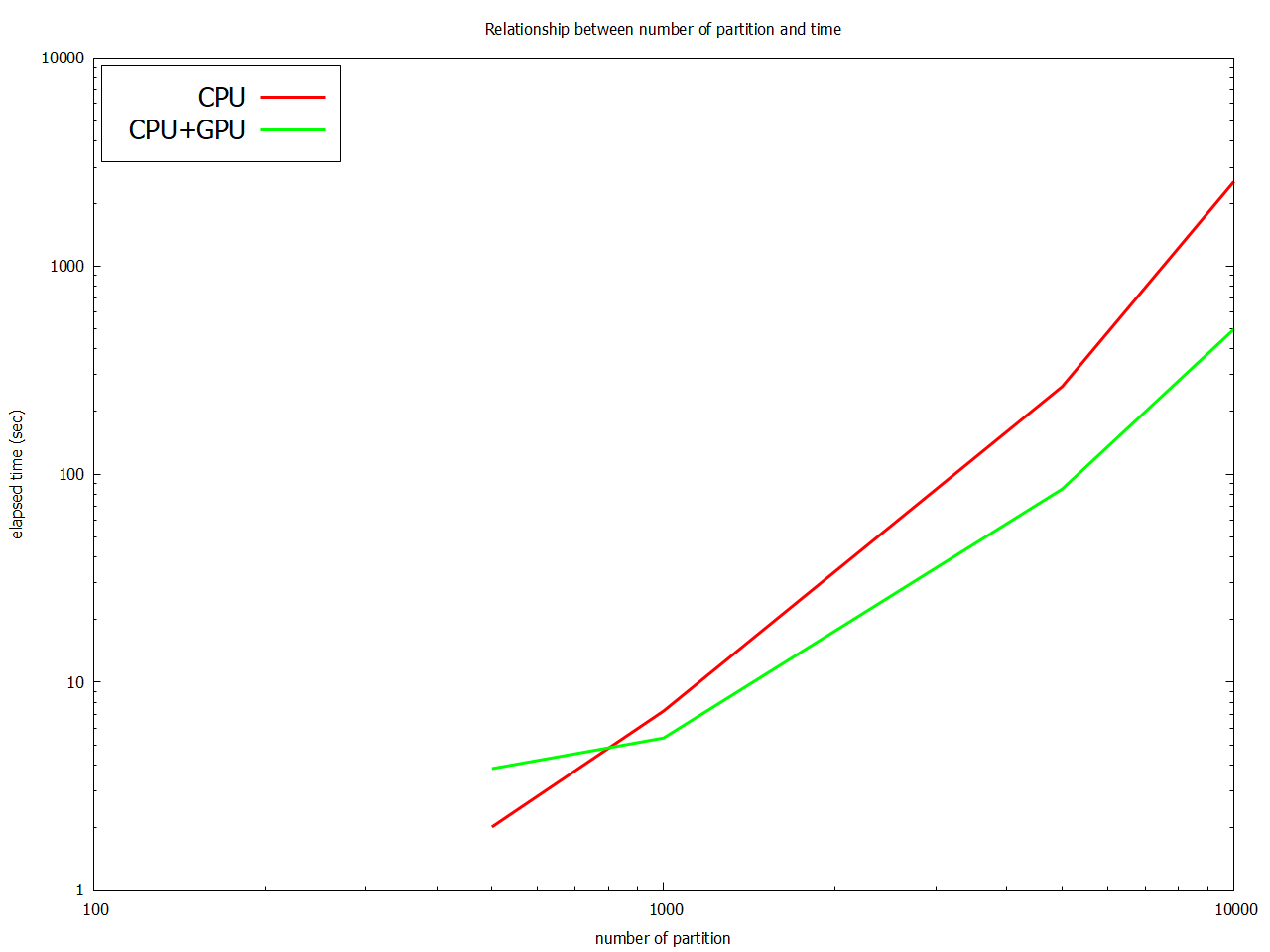
また,上記の結果を以下にグラフで示します.
分割数が1000以上では,CPUよりCPU+GPUの方が高速になります.分割数10000では,CPUよりCPU+GPUの方が5倍以上高速です.ただし,CPUとCPU+GPUでは,計算の結果に違いが出てしまうことに注意が必要です.たとえば,分割数5000,カットオフ$ r_c = 50.0(a.u.) $,$ \left\vert E_{new}-E_{old}\right\vert $の閾値$ 5 \times 10^{-12} $のとき,CPUではenergy = -2.86157824923450だったのに対し,CPU+GPUでは,energy = -2.86157824922418であり,小数点以下11桁以下が異なる結果となりました.また,分割数5000,カットオフ$ r_c = 50.0(a.u.) $,$ \left\vert E_{new}-E_{old}\right\vert $の閾値$ 5 \times 10^{-13} $のとき,CPUではSCFの繰り返し回数が23回で収束しましたが,CPU+GPUでは,収束までにSCFの繰り返し回数が68回も必要になりました.ただしこの結果をもって,「CPUよりGPUの方が精度が悪い」とは一概に言えないと思います.
なお,CPU+GPUのコードは,GitHubのこちらで公開しています.