この記事では,第一原理計算で非常によく用いられる擬ポテンシャルについて解説します.なお,この記事はGPT-5 ThinkingなどのLLMを積極的に利用しています.その点をご承知おきください
擬ポテンシャルの概説
擬ポテンシャルとは,原子核と内殻電子の影響をあらかじめ一つの「有効(イオン)ポテンシャル」にまとめ,価電子だけを明示的に扱えるようにする手法です.内殻電子はエネルギー的に深く化学的にほぼ不活性で,分子や固体中でも状態が大きく変わりにくいという事実に基づいています.孤立原子に対して,あらかじめ核のクーロンポテンシャルに内殻電子の効果を組み入れた有効ポテンシャルを作っておけば,固体などの複雑な系でも価電子の計算を大幅に簡略化できます.実際,この方法は散乱特性の再現やノルム保存条件などの理論的根拠に加え,多数の計算的・実験的検証によって妥当性が裏付けられています.以下で,擬ポテンシャルについて詳しく説明します.
直交化平面波(OPW)法
擬ポテンシャルについて説明する前に,直交化平面波(Orthogonalized Plane Wave, OPW)法について説明します.解きたい問題は,「固体中の電子のハミルトニアンを平面波基底で展開して,内殻および価電子状態を求める」ことです.ところが実際の原子のポテンシャルは原子核の近くで非常に深く,急峻です.すると価電子の波動関数は,内殻電子との規格直交条件を満たすため核近傍で激しく振動します.これは,価電子の波動関数の核近傍を平面波で表すには非常にたくさんの基底関数が必要になる,ということを意味しています.しかし一方で,価電子状態は必ず内殻状態と直交しているので,それならば「最初から内殻状態に直交した基底」を使えば,価電子だけを効率的に展開できるのではないか?という考え方がOPW法です.
内殻状態と価電子状態
最初から詳しく説明していきます.まず,結晶中の電子のKohn-Sham方程式は,
H \Psi(\mathbf{r})=\left(-\frac{\hbar^2}{2 m} \nabla^2+v(\mathbf{r})\right) \Psi(\mathbf{r})=\varepsilon \Psi(\mathbf{r}) \quad(1)
と書けます.ここで$v(\mathbf{r})$は全電子KSポテンシャル(凍結コア近似を使うのでコアは固定)です.原子ごとの内殻状態$\phi_c\left(\mathbf{r}-\mathbf{R}_n\right)$を考え,それを格子全体に展開して作ったBloch波
\Phi_{c k}(\mathbf{r})=\frac{1}{\sqrt{N}} \sum_n e^{i \mathbf{k} \cdot \mathbf{R}_n} \phi_c\left(\mathbf{r}-\mathbf{R}_n\right) \quad(2)
が与えられているとします(これは正確には凍結コア近似です).ここで,
- $c$ は内殻軌道の種類( $1 s, 2 s, 2 p, \ldots$ など)
- $n$ は格子点のインデックス
- $N$ は格子点の総数
です.
内殻状態は規格直交なので,
\int d^3 r \phi_c^*\left(\mathbf{r}-\mathbf{R}_n\right) \phi_{c^{\prime}}\left(\mathbf{r}-\mathbf{R}_{n^{\prime}}\right) \simeq \delta_{cc^{\prime}} \delta_{nn^{\prime}} \quad(3)
が成り立ちます(正確には重なりはゼロではありませんが,深い内殻では重なりを無視できます).(3)式から,Bloch波$\Phi_{c \mathbf{k}}$も($\mathbf{k}$点が離散化されていると仮定して)
\int d^3 r \Phi_{c \mathbf{k}}^*(\mathbf{r}) \Phi_{c^{\prime} \mathbf{k}^{\prime}}(\mathbf{r}) \simeq \delta_{c c^{\prime}} \delta_{\mathbf{k} \mathbf{k}^{\prime}} \quad(4)
を(近似的に)満たします(これは波数が違えば直交するという普通のBloch波の直交性を意味しています).凍結コア近似を使い,孤立原子コアが結晶中でもほぼ固有状態とみなせると仮定すれば,近似的に
H \Phi_{c \mathbf{k}}(\mathbf{r}) \simeq \varepsilon_c \Phi_{c \mathbf{k}}(\mathbf{r}) \quad(5)
が成り立っています.そして,ハミルトニアンはHermitianなので,固有値が異なる固有状態は直交します.すなわち,価電子状態 $\Psi_{\mathbf{k}}$ は内殻状態 $\Phi_{c \mathbf{k}}$ と直交していて,
\left\langle\Phi_{c \mathbf{k}} \mid \Psi_{\mathbf{k}}\right\rangle=0 \quad(6)
となります.これは先ほど述べた,「価電子状態は内殻状態に直交している」ことを示しています.
OPWの定義
普通の平面波基底を
\phi_{\mathbf{k}-\mathbf{G}}(\mathbf{r})=\frac{1}{\sqrt{\Omega}} e^{i(\mathbf{k}-\mathbf{G}) \cdot \mathbf{r}} \quad(7)
と書きます($\Omega$は単位胞体積です).これを内殻状態に対してGram-Schmidtの直交化を行うと,直交化平面波(OPW)が得られます.すなわち,
\chi_{\mathbf{k}, \mathbf{G}}(\mathbf{r})=\phi_{\mathbf{k}-\mathbf{G}}(\mathbf{r})-\sum_c\left\{\int d^3 r^{\prime} \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \phi_{\mathbf{k}-\mathbf{G}}\left(\mathbf{r}^{\prime}\right)\right\} \Phi_{c \mathbf{k}}(\mathbf{r}) \quad(8)
です.(8)式をブラケット記号を用いて書き換えると,
\left|\chi_{\mathbf{k} \mathbf{G}}\right\rangle=\left|\phi_{\mathbf{k}-\mathbf{G}}\right\rangle-\sum_c\left|\Phi_{c \mathbf{k}}\right\rangle\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle \quad(9)
となります.(9)式から,OPWは,平面波から「内殻状態への射影成分」を引き落としたものであることが分かります.
OPWの種々の内積の確認
さてこの定義で,本当に$\chi_{k \mathbf{G}}$が内殻に直交しているかを確かめてみましょう.
\begin{aligned}
\left\langle\Phi_{c \mathbf{k}} \mid \chi_{\mathbf{k} \mathbf{G}}\right\rangle & =\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle-\sum_{c^{\prime}}\left\langle\Phi_{c \mathbf{k}} \mid \Phi_{c^{\prime} \mathbf{k}}\right\rangle\left\langle\Phi_{c^{\prime} \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle \\
& =\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle-\sum_{c^{\prime}} \delta_{c c^{\prime}}\left\langle\Phi_{c^{\prime} \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle \\
& =\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle-\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle=0 \quad(10)
\end{aligned}
となり,OPWは確かに内殻状態と完全に直交しています.従って,価電子状態をOPWの線形結合で表せば,「価電子状態は内殻と直交している」という条件は,基底の選び方だけで自動的に満たされることになります.ただし,$\chi_{\mathbf{k} \mathbf{G}}$同士は直交していません.実際に内積を計算すると,
\begin{aligned}
\left\langle\chi_{\mathbf{k}, \mathbf{G}} \mid \chi_{\mathbf{k}, \mathbf{G}^{\prime}}\right\rangle & =\left\langle\phi_{\mathbf{k}-\mathbf{G}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle-\sum_c\left\langle\phi_{\mathbf{k}-\mathbf{G}} \mid \Phi_{c \mathbf{k}}\right\rangle\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \\
& =\delta_{\mathbf{G}, \mathbf{G}^{\prime}}-\sum_c\left\langle\phi_{\mathbf{k}-\mathbf{G}} \mid \Phi_{c \mathbf{k}}\right\rangle\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \quad(11)
\end{aligned}
となり,直交していないことが分かります.つまり,OPWは「内殻とは直交しているが,互いには直交していない非直交基底」です.また,平面波とも直交していないことに注意してください.これも実際に内積を計算してみると,
\begin{aligned}
\left\langle\chi_{\mathbf{k}, \mathbf{G}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle & =\left\langle\phi_{\mathbf{k}-\mathbf{G}}-\sum_c \Phi_{c \mathbf{k}}\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \\
& =\left\langle\phi_{\mathbf{k}-\mathbf{G}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle-\sum_c\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle^*\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \quad(12)
\end{aligned}
ここで
\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}}\right\rangle^*=\left\langle\phi_{\mathbf{k}-\mathbf{G}} \mid \Phi_{c \mathbf{k}}\right\rangle \quad(13)
なので,より対称な形に書くと
\left\langle\chi_{\mathbf{k}, \mathbf{G}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle=\delta_{\mathbf{G}, \mathbf{G}^{\prime}}-\sum_c\left\langle\phi_{\mathbf{k}-\mathbf{G}} \mid \Phi_{c \mathbf{k}}\right\rangle\left\langle\Phi_{c \mathbf{k}} \mid \phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \quad(14)
となり,(14)式は(11)式と全く同じ式となり,確かに直交していないことが分かります.
価電子状態の展開と固有値方程式
ここで,価電子バンドのBloch状態$\Psi_k(\mathbf{r})$をOPWで展開すると,
\Psi_{\mathbf{k}}(\mathbf{r})=\sum_{\mathbf{G}} a_{\mathbf{G}}(\mathbf{k}) \chi_{\mathbf{k}, \mathbf{G}}(\mathbf{r}) \quad(15)
これをKohn-Sham方程式
H \Psi_k=\varepsilon \Psi_k \quad(16)
に代入し,左から $\left\langle\chi_{k, \mathbf{G}}\right|$ をかけて積分すれば,
\sum_{\mathbf{G}^{\prime}}\left\langle\chi_{k, \mathbf{G}}\right| H-\varepsilon\left|\chi_{k, \mathbf{G}^{\prime}}\right\rangle a_{\mathbf{G}^{\prime}}(k)=0 \quad(17)
という問題になります.(17)式に非自明解がある条件は,
\operatorname{det}\left\langle\chi_{k, G}\right| H-\varepsilon\left|\chi_{k, G^{\prime}}\right\rangle=0 \quad(18)
です.
有効ポテンシャルの導入
さて問題は, $\langle\chi| H|\chi\rangle$ をどう書き直すかです.ハミルトニアンは
H=-\frac{\hbar^2}{2 m} \nabla^2+v(\mathbf{r}) \quad(19)
で, $v(\mathbf{r})$ は(1)式の定義の通りです.平面波間の行列要素
\left\langle\phi_{\mathbf{k}-\mathbf{G}}\right| H\left|\phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \quad(20)
は,
- 運動エネルギー部分 :$\frac{\hbar^2}{2 m}|\mathbf{k}-\mathbf{G}|^2 \delta_{\mathbf{G}, \mathbf{G}^{\prime}}$
- ポテンシャル部分:$v_{\mathbf{G}, \mathbf{G}^{\prime}}$(ポテンシャルのFourier成分)
に分かれます.ここで,
\left\langle\phi_{\mathbf{k}-\mathbf{G}}\right| H\left|\phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle=\frac{\hbar^2}{2 m}|\mathbf{k}-\mathbf{G}|^2 \delta_{\mathbf{G}, \mathbf{G}^{\prime}}+v_{\mathbf{G}, \mathbf{G}^{\prime}} \quad(21)
となります.$v_{\mathbf{G}, \mathbf{G}^{\prime}}$の具体的な形は,周期系なら,
v_{\mathbf{G}, \mathbf{G}^{\prime}}=\frac{1}{\Omega} \int_{\Omega} d^3 r e^{i\left(\mathbf{G}-\mathbf{G}^{\prime}\right) \cdot \mathbf{r}} v(\mathbf{r}) \quad(22)
です.OPWの定義を代入して $\langle\chi| H|\chi\rangle$ を展開し, $H \Phi_{c \mathbf{k}}=\varepsilon_c \Phi_{c \mathbf{k}}$と内殻の直交性$\left\langle\Phi_{c \mathbf{k}} \mid \Phi_{c^{\prime} \mathbf{k}}\right\rangle=\delta_{c c^{\prime}}$を使って整理すると,結果として,
\begin{aligned}
\left\langle\chi_{\mathbf{k}, \mathbf{G}}\right| H-\varepsilon\left|\chi_{\mathbf{k}, \mathbf{G}^{\prime}}\right\rangle= & \left\{\frac{\hbar^2}{2 m}|\mathbf{k}-\mathbf{G}|^2-\varepsilon\right\} \delta_{\mathbf{G}, \mathbf{G}^{\prime}} +v_{\mathbf{G}, \mathbf{G}^{\prime}}+\left(v_R\right)_{\mathbf{G}, \mathbf{G}^{\prime}} \quad(23)
\end{aligned}
という形になります.ここに出てくる $\left(v_R\right)_{\mathbf{G}, \mathbf{G}^{\prime}}$ が非局所斥力ポテンシャルです.
位置表示は
v_R\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\sum_c \Phi_{c \mathbf{k}}(\mathbf{r})\left(\varepsilon-\varepsilon_c\right) \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \quad(24)
と書けます.これは演算子としては
\hat{v}_R=\sum_c\left(\varepsilon-\varepsilon_c\right)\left|\Phi_{c \mathbf{k}}\right\rangle\left\langle\Phi_{c \mathbf{k}}\right| \quad(25)
という「内殻状態への射影演算子」に$\left(\varepsilon-\varepsilon_c\right)$をかけたものです.価電子のエネルギー$\varepsilon$は内殻より高いので,$\left(\varepsilon-\varepsilon_c\right)>0$であり,これが「斥力的(repulsive)」と呼ばれる理由です.直感的には,内殻状態の空間に入ろうとする成分を強く押し上げるイメージです.
OPWと平面波+有効ポテンシャルの等価性
ここで重要なことは,OPW基底での行列要素は,「平面波基底で,別の有効ハミルトニアンを使う」問題に書き換えられるという点です.ここで,
\left\langle\chi_{\mathbf{k}, \mathbf{G}}\right|\left(-\frac{\hbar^2}{2 m} \nabla^2+v\right)-\varepsilon(\mathbf{k})\left|\chi_{\mathbf{k}, \mathbf{G}^{\prime}}\right\rangle=\left\langle\phi_{\mathbf{k}-\mathbf{G}}\right|\left(-\frac{\hbar^2}{2 m} \nabla^2+\Gamma\right)-\varepsilon(\mathbf{k})\left|\phi_{\mathbf{k}-\mathbf{G}^{\prime}}\right\rangle \quad(26)
を考えます.ただし,
\Gamma=v+v_R \quad(27)
です.こうすると(26)式の右辺にはOPWは出てこず,普通の平面波と「有効ポテンシャル$\Gamma$」だけが出てきます.つまり,
- 「本物のハミルトニアン $H$ と OPW基底」
- 「有効ハミルトニアン $H_{\mathrm{eff}}=-\frac{\hbar^2}{2 m} \nabla^2+\Gamma$ と普通の平面波」
は,価電子の固有値問題に関しては等価,ということになります.
ここで$\Gamma$をエネルギー依存の「擬ポテンシャルの原型」と読み替えると,OPW法は擬ポテンシャル法の一種の導出になっているわけです.
より一般的な非局所ポテンシャルv_Rと擬波動関数
さて,先ほどの$v_R$は特定の形
v_R\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\sum_c \Phi_{c \mathbf{k}}(\mathbf{r})\left(\varepsilon-\varepsilon_c\right) \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \quad(28)
でしたが,もっと一般の形,
v_R\left(r, r^{\prime}\right)=\sum_c \Phi_{c k}(r) F_c^*\left(r^{\prime}\right) \quad(29)
を考えてみましょう.ここで$F_c\left(\mathbf{r}^{\prime}\right)$は任意の関数(演算子核)です. つまり,内殻状態$\Phi_{c \mathbf{k}}$への射影を使った任意の非局所ポテンシャルです.このとき,本物の問題
\left(-\frac{\hbar^2}{2 m} \nabla^2+v\right) \Psi=\varepsilon \Psi \quad(30)
と,擬ポテンシャルを含んだ「擬問題」
\left(-\frac{\hbar^2}{2 m} \nabla^2+v+v_R\right) \Phi=\varepsilon^{\prime} \Phi \quad(31)
を考えます.ここで$\Psi$を「本物の波動関数」,$\Phi$を「擬波動関数」と呼んでいます.両者が「価電子状態」であり,内殻状態とは直交している,つまり
\left\langle\Psi \mid \Phi_{c \mathbf{k}}\right\rangle=0, \quad\left\langle\Phi_{c \mathbf{k}} \mid \Phi\right\rangle=0 \quad(32)
と仮定します(価電子は内殻と直交する,という条件).擬問題の式の左から$\Psi^*$をかけて積分すると,
\langle\Psi|-\frac{\hbar^2}{2 m} \nabla^2+v|\Phi\rangle+\langle\Psi| v_R|\Phi\rangle=\varepsilon^{\prime}\langle\Psi \mid \Phi\rangle \quad(33)
ここで,
v_R=\sum_c\left|\Phi_{c \mathbf{k}}\right\rangle\left\langle F_c\right| \quad(34)
という形を思い出すと,
\langle\Psi| v_R|\Phi\rangle=\sum_c\left\langle\Psi \mid \Phi_{c \mathbf{k}}\right\rangle\left\langle F_c \mid \Phi\right\rangle=0 \quad(35)
となるので,擬ポテンシャルの寄与は消えてしまいます(ここで,$\left\langle\Psi \mid \Phi_{c \mathbf{k}}\right\rangle=0$を使いました).一方,本物の方程式
\left(-\frac{\hbar^2}{2 m} \nabla^2+v\right) \Psi=\varepsilon \Psi \quad(36)
に左から$\Phi^*$をかけて積分し,ハミルトニアンがHermitianであることを使うと,
\langle\Psi|-\frac{\hbar^2}{2 m} \nabla^2+v|\Phi\rangle=\varepsilon\langle\Psi \mid \Phi\rangle \quad(37)
となります.従って,
\varepsilon^{\prime}\langle\Psi \mid \Phi\rangle=\varepsilon\langle\Psi \mid \Phi\rangle \quad \Rightarrow \quad \varepsilon^{\prime}=\varepsilon \quad(38)
となります(ただし,$\langle\Psi \mid \Phi\rangle \neq 0$を仮定).これから,「選んだコア直交サブスペース内の価電子固有値は$v_R$によらない自由度があり,擬ポテンシャルは非一意である」ということがわかります.
OPW法とAshcroftの空内殻(empty-core)ポテンシャル
OPW法で出てきた
v_R\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\sum_c \Phi_{c \mathbf{k}}(\mathbf{r})\left(\varepsilon-\varepsilon_c\right) \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \quad(39)
は,「一般形」
v_R\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\sum_c \Phi_{c \mathbf{k}}(\mathbf{r}) F_c\left(\mathbf{r}^{\prime}\right) \quad(40)
に対して,
F_c\left(\mathbf{r}^{\prime}\right)=\left(\varepsilon-\varepsilon_c\right) \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \quad(41)
と選んだ場合になっています.これはエネルギー依存の非局所ポテンシャルですが,それでも価電子サブスペースに関しては正しい固有値を与えます.別の選び方として,
F_c\left(\mathbf{r}^{\prime}\right)=-\Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) v\left(\mathbf{r}^{\prime}\right) \quad(42)
を用いると,有効ポテンシャルは
\begin{aligned}
\Gamma\left(\mathbf{r}, \mathbf{r}^{\prime}\right) & =v(\mathbf{r}) \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)+v_R\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \\
& =v(\mathbf{r}) \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)-\sum_c \Phi_{c \mathbf{k}}(\mathbf{r}) \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) v\left(\mathbf{r}^{\prime}\right) \quad(43)
\end{aligned}
となります.さらに,「内殻状態が核のまわりのある領域$r<r_c$で完全系をなしている」と仮定すると,その領域では
\sum_c \Phi_{c \mathbf{k}}(\mathbf{r}) \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \simeq \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right) \quad \text { for } r, r^{\prime}<r_c \quad(44)
と近似できます.すると$r=r^{\prime}<r_c$では
\Gamma\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \simeq v(\mathbf{r}) \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)-v(\mathbf{r}) \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)=0 \quad(45)
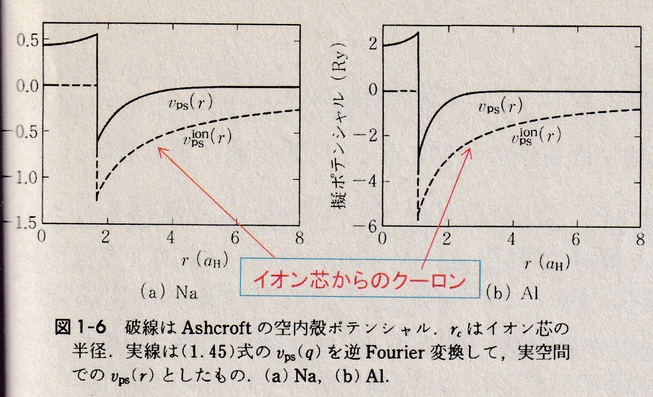
となります.つまり,核の近く(コアの内側)では有効ポテンシャルがゼロになります.つまり,その領域では電子が自由粒子のように振る舞うことを意味します.ただし,核の外側ではポテンシャルが残る(または調整される)ので,価電子の散乱位相(位相シフト)がちゃんと再現されるよう調整しておく必要があります(詳しくは述べませんが,擬ポテンシャルは散乱問題と深い関係があります).これがAshcroftの「空内殻(empty-core)ポテンシャル」の基本的な考え方です.核の近くのクーロンポテンシャルによる急激な価電子波動関数の振動を,「コアの中は真空(ポテンシャルがゼロ)」に置き換えることで,価電子波動関数を滑らかにして,少ない平面波で展開できるようにしています.具体的に数式で表すと,
v_{ps}^{ion}(r)= \begin{cases}0 & \left(r<r_c\right) \\ -\frac{z e^2}{4 \pi \epsilon_0 r} & \left(r>r_c\right)\end{cases} \quad(46)
です.つまり,
- 核近傍$r<r_c$ではポテンシャルがゼロ
- それより外側$r>r_c$では裸のクーロン $-z e^2 / (4\pi \epsilon_0 r)$
となります.ここで$z$は価電子数です.さらに固体中では価電子(自由電子的)がイオン芯の電場を遮蔽し,「核の強いポテンシャル」と「規格直交化とPauli反発による排除効果」の合成が,見かけ上の弱いポテンシャルを作りだします.その結果,固体中の価電子が見るポテンシャル(のFourier成分)$v_{ps}(q)$は,
v_{ps}(q)=v_{ps}^{ion}(q) / \epsilon(q) \quad(47)
となります.ここで,
- $v_{ps}^{ion}(q)$ :イオン芯の「裸」のポテンシャル(のFourier成分)
- $\varepsilon(q)$ :価電子による遮蔽(誘電関数)
です.つまり「核のポテンシャルを価電子が遮蔽して弱め」ています.$\epsilon(q)$の具体的な式は,
\begin{aligned}
& \epsilon(q)=1+\frac{q_{T F}^2}{q^2}\left\{\frac{1}{2}+\frac{4 k_F^2-q^2}{8 k_F q} \ln \left|\frac{2 k_F+q}{2 k_F-q}\right|\right\} \quad(48) \\
& n=\frac{z}{\Omega} \quad(49) \\
& k_F =\left(3 \pi^2 n\right)^{1 / 3} \quad(50) \\
& q_{TF}=\left(\frac{3 n e^2}{2 \varepsilon_0 \varepsilon_F}\right)^{1 / 2}, \quad \varepsilon_F=\frac{\hbar^2 k_F^2}{2m} \quad(51)
\end{aligned}
となります.(48)式はLindhard誘電関数と呼ばれます。ここで,$n$は1原子あたり価電子数$z$と原子1個あたりの体積$\Omega$から決まる電子密度,$k_F$は,自由電子ガスのフェルミ波数,$q_{TF}$はThomas–Fermi遮蔽波数であり,遮蔽の効きやすさ(遮蔽長の逆数)を表します($q_{TF}$が大きいほど遮蔽は短距離で強く効き,ポテンシャルはより弱く見えます).下図の実線は価電子が感じる弱められた有効ポテンシャル$v_{\mathrm{ps}}(r)$($v_{ps}(q)$をFourier逆変換したもの)ですが,価電子による遮蔽を入れる前の「元の強いポテンシャル」である$v_{ps}^{ion}(r)$($v_{ps}^{ion}(q)$をFourier逆変換したもの)と比べて,ずっと浅くなっていることが分かります.
擬ポテンシャル
重要なのは,「Ashcroftの空内殻(empty-core)ポテンシャル」の$r_c$が何を表しているかです.これは「本当にポテンシャルがゼロの半径」というより,「核近傍は規格直交化・Pauli反発で価電子が実効的に近づけない領域」の半径をパラメータ1個で粗く代表させたもの,と解釈できます.つまりAshcroftは,「内殻を捨てる」,「核近傍の細かい構造を捨てる」,「外側の散乱・結合に効く部分だけ残す」という擬ポテンシャルの発想を,最小限の形で実装したといえます.このAshcroftの空内殻ポテンシャルは,NaやAlのような「ほぼ自由電子金属」なら驚くほど有効です.なぜなら,こういった金属では価電子が感じているポテンシャル自体が弱く,細部よりも「弱い散乱の強さ」だけ合っていればバンドやフォノンがほぼ決まるからです.しかしAshcroftモデルは,あまりに単純すぎ,物理的に割り切りすぎています.主な弱点は3つあります.
- 局所(local)である.つまり,実際の規格直交化効果は角運動量$l$ごとに違うのに,Ashcroftモデルはそれを全部ひとまとめにしてしまっている.
- 原子環境が変わっても同じ$r_c$で通る保証がないので,移植性(transferability)が低い.例えば,同じ元素でも,金属,半導体,酸化物で価電子の入り込み方が変わる.つまり,経験的に決めた$r_c$では別環境で外れることがある.
- 散乱(位相シフト)を厳密に保存する仕組みがない.「外側が合っていればOK」という希望的観測があるだけで,理論的な保証が薄い.
以上の3つからなる,「モデル擬ポテンシャルの限界」から,擬ポテンシャルに対する要求は以下のようにまとめられることになりました.
- 核近傍を滑らかに捨て,計算を軽くしたい.
- しかし価電子の散乱特性は精度とtransferabilityのため本物と同じ必要がある.
ここで登場するのがすでに出てきた擬波動関数を基準に作る非経験的擬ポテンシャルです.
非経験的擬ポテンシャル
非経験的擬ポテンシャルとして,まずはノルム保存擬ポテンシャル(Norm-Conserving PseudoPotential, NCPP)を考えます(ウルトラソフト擬ポテンシャルやPAW法は後で考えます).NCPPの作成には
- まず原子に対する全電子計算で,真の価電子波動関数$\phi_t(r)$ を得る.
- それを元に,コア内$r < r_c$(この$r_c$をカットオフ半径と呼びます)を滑らかにした擬波動関数 $\phi_{ps}(r)$を作る.
- その $\phi_{ps}$ が真の散乱を再現するように,条件を課す.
- その条件を満たすポテンシャル $v_{ps}$ を逆算する.
という手順を踏みます.ここで,手順3で課す条件は,Hamann, SchluterとChiangの条件(HSC条件)として知られています.HSC条件を具体的に書くと,
- 擬ポテンシャルによる価電子の固有値が,原子の選ばれた基準配置における全電子ポテンシャルの固有値と一致すること.
- 価電子の擬波動関数はカットオフ半径$r_c$の外では全電子波動関数と一致すること.
- 価電子の擬波動関数の$r_c$での対数微分は全電子のものと一致すること.
- 全電子波動関数と擬波動関数の,$r_c$内部における積分電荷が一致すること(ノルム保存条件).
- 全電子波動関数と擬波動関数の対数微分の1次のエネルギー微分は$r_c$で一致し,従ってすべての$r > r_c$でも一致すること
です.HSC条件の2~5は,数学的には以下の(1)~(3)の条件にまとめられます.
(1) $r \geq r_c$では$\phi_{ps}(r)=\phi_t(r)$かつ$r=r_c$で滑らかにつながる.
このことにより,HSC条件の2番が満たされます.
(2) 対数微分$D_l(\varepsilon)=\left[\frac{\partial R_l(r ; \varepsilon)}{\partial r} / R_l(r ; \varepsilon)\right]_{r=r_c}$およびその一次のエネルギー微分が全電子波動関数と擬波動関数で等しくなる.
この条件によりHSC条件の3番と5番が満たされます.対数微分は散乱ポテンシャルの位相シフトを決めるので,このことは,擬ポテンシャルによる散乱が全電子によるポテンシャルによる散乱と同じになることを保証します.
(3) ノルム保存条件
\int_{r<r_c} d^3 r\left|\phi_{ps}(r)\right|^2=\int_{r<r_c} d^3 r\left|\phi_t(r)\right|^2 \quad(52)
これはHSC条件の4番に対応します.静電ポテンシャルを正しく与えるためには,この条件が必要です.さらに,擬波動関数を滑らかにするため以下の条件が追加で要求されます.
(4) 価電子の擬波動関数が$r<r_c$で節(ノード)を持たない.
この条件により,最低エネルギー状態が価電子の状態になり,内殻状態は現れないようになります.なお,HSC条件の1番を満たすためには擬ポテンシャルを調整する必要があります.
ここで重要な点は,条件(2)のエネルギー微分一致です.これはあるエネルギーのところでの,擬ポテンシャルの散乱が全電子によるポテンシャルの散乱と同じになるだけでなく,ノルム保存の条件から,そのエネルギーの近傍のエネルギーに対しても,擬ポテンシャルの散乱の記述が正しいことを保証します.さらに,原子の固有状態のエネルギーと,固体の固有状態のエネルギーは少しずれますが,そのずれたエネルギーでも,擬ポテンシャルの散乱の記述は正しくなることも保証します.
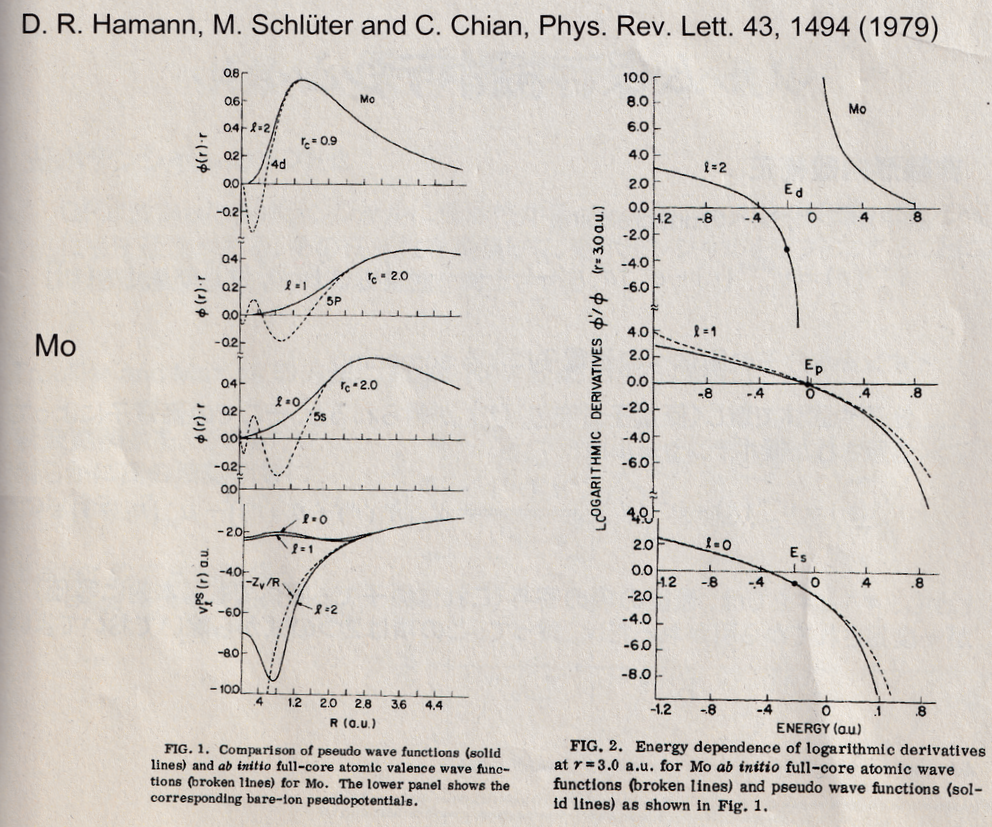
以下に,Moの全電子波動関数と擬波動関数の比較図,全電子波動関数の対数微分と擬波動関数の対数微分のエネルギー依存性の比較図を示します.
擬ポテンシャルの非局所性
これまで,NCPPについて説明してきました.ここで忘れてはいけないことは,電子状態は角運動量$l$によって原子核近傍での振る舞いが大きく異なることです.たとえば$s, p, d, f$ではノードの数や浸透のしかたが違い,同じ$r_c$依存ポテンシャルでは全ての$l$成分の散乱を同時に合わせることができません.そこで,擬ポテンシャルは各角運動量チャネルごとに独立に条件を満たすように構成されます.これが擬ポテンシャルが$l$依存性を持つ理由であり,このため擬ポテンシャルは非局所演算子となりますが,その核が半径方向で局所的なので半局所(semi-local)と呼びます.典型的には,次式のように,ある基準となる局所ポテンシャル$v_{local}(r)$を一つ選び,そこから各$l$チャネルの差分$\delta v_l(r)$を射影演算子で付け足す形に書きます.
v_{S L}=v_{local}(r)+\sum_{l, m}\left|Y_{l m}\right\rangle \delta v_l(r)\left\langle Y_{l m}\right| \quad(53)
ここで$\left|Y_{l m}\right\rangle$は球面調和関数で, $\sum_m\left|Y_{l m}\right\rangle\left\langle Y_{l m}\right|$ は「角運動量$l$成分だけを取り出す射影演算子」に相当します.つまり(53)式は,「角運動量成分ごとに異なる半径方向ポテンシャルを作用させる」ことを意味しています.より一般の非局所擬ポテンシャル(Kleinman-Bylander形式)では,このsemi-local形をさらに計算効率の良い形へ変形しますが,それは後で述べます.
内殻補正
価電子の状態は,原子が固体中でどのような環境に置かれるかによって大きく変化します.一方,価電子を取り除いたイオン部分(核+内殻電子)の電荷分布は比較的環境に依存しにくいです.従って,中性原子の全電子計算から作った擬ポテンシャルから,イオンに対応する「裸の擬ポテンシャル」を抜き出す(unscreening)ことを考えます.ただし,このunscreeningには二つの注意点があります.
- 交換相関ポテンシャルの非線形性
Kohn-Shamの交換相関ポテンシャル$v_{xc}[n]$は電子密度 $n(r)$の非線形汎関数です.よって「内殻+価電子密度に対する$v_{xc}$」から「内殻だけの$v_{xc}$」を引き算して…という操作が,単純な線形操作としては扱えません.この問題を扱うのが非線形内殻補正(NonLinear Core Correction, NLCC)です. - 内殻密度の急峻さ
内殻電子の密度$n_c(r)$は核近傍で非常に急激に変化するので,擬ポテンシャル計算(特に平面波基底)では数値的に扱いづらいです.従って,内殻密度の寄与をどこまでどのような形で取り込むかに工夫が必要になります.この近似が,いわゆる部分内殻補正(Partial Core Correction, PCC)です.実装上はNLCCを具体化する代表的な手法として広く使われています.
中性原子で得られた「遮蔽された」擬ポテンシャル $V_{ps}^{atom}(r)$ から,価電子密度 $n_v^a(r)$ が作るハートリー項と,価電子を含む交換相関項を取り除くと,イオンの擬ポテンシャルは
v_{ps}^{\text {ion }}(r)=v_{ps}^{\text {atom }}(r)-e^2 \int d^3 r^{\prime} \frac{n_v^a\left(r^{\prime}\right)}{\left|r-r^{\prime}\right|}-v_{xc}\left[n_c(r)+n_v^a(r)\right]+v_{xc}\left[n_c(r)\right] \quad(54)
と書けます.右辺の第2項は「原子価電子が作るクーロン遮蔽の除去」,第3項および第4項は「価電子を含む交換相関の除去」を表します.非線形であるがゆえに,交換相関項は$n_c+n_V$と$n_c$の差として正確に取り扱う必要がある,というのがNLCCのポイントです.
固体の計算では,新しい価電子密度$n_v^s(r)$が自己無撞着に決まります.すると,その価電子によって再び遮蔽された擬ポテンシャルは,
v_{ps}^s(r)=v_{ps}^{ion}(r)+e^2 \int d^3 r^{\prime} \frac{n_v^s\left(r^{\prime}\right)}{\left|r-r^{\prime}\right|}+v_{xc}\left[n_c(r)+n_v^s(r)\right]-v_{xc}\left[n_c(r)\right] \quad(55)
となります.第2項は固体価電子によるハートリー遮蔽の付与,第3項および第4項は「内殻密度を背景にした交換相関の再付与」を意味します.ここで,(54)式と(55)式を見比べると,$-v_{xc}\left[n_c\right]+v_{xc}\left[n_c\right]$のような内殻だけの交換相関項は,unscreeningとscreeningの過程で一度差し引かれてから再び足されるだけで,原子と固体で本質的に等価な寄与です.従って計算上は,この往復するだけの項を最初から除去しておいてよいことが分かります.
部分内殻補正(Partial Core Correction, PCC)
(54)式,(55)式の形そのものは正しいです.しかし,平面波基底のように滑らかな基底で計算する場合,内殻電子の密度$n_c(r)$がそのまま現れると,核近傍の急峻な構造のために多数の平面波を必要とし,展開の収束性が著しく悪化します.そこで「内殻密度をそのまま使うのではなく,価電子と重なる領域に限って,滑らかにした内殻密度を使う」という近似を導入します.これがPCCです.
もし価電子密度と内殻密度が空間的に重ならなければ,
v_{xc}\left[n_c(r)+n_v(r)\right] \simeq v_{xc}\left[n_c(r)\right]+v_{xc}\left[n_v(r)\right] \quad(56)
となり,交換相関の非線形性は事実上問題になりません.従って重要なのは,価電子が内殻領域に浸透して重なる部分だけであり,その領域に限定して部分内殻密度$n_c^{partial}(r)$を次式のように導入します.
n_c^{partial}(r)=\begin{cases}\frac{A \sin (B r)}{r} & \left(r \leq r_0\right) \\
n_c(r) & \left(r \geq r_0\right)\end{cases} \quad(57)
ここで$r_0$は価電子と内殻が重なり始める程度の半径です.$r_0$より内側では滑らかな関数 $\frac{A \sin (B r)}{r}$ に置き換えることで,平面波展開の収束性と数値安定性を確保します.$r_0$より外側では本来の内殻密度 $n_c(r)$ をそのまま用いるため,価電子との重なり領域における交換相関の非線形効果は保たれます.この「精度に効く部分だけ残して,数値的に厳しい部分を滑らかにする」という割り切りが,部分内殻補正の狙いです.
種々のNCPP
OPW法からの擬ポテンシャルに任意性があったように,NCPPにも任意性があります.その任意性を調整して,擬ポテンシャルをソフトにすることにより,平面波展開などにおける収束性を向上させます.このような擬ポテンシャルとして,BHS擬ポテンシャル,Kerker擬ポテンシャル,Troullier−Martins擬ポテンシャル(TM擬ポテンシャル)やMorrison-Bylander-Kleinmanの擬ポテンシャル(MBK擬ポテンシャル)などがあります.TM擬ポテンシャルについては後で詳しく解説します.
Kleinman–Bylander (KB)分離形
ここまで見てきたように,semi-local形式の非局所擬ポテンシャルは,
v_{S L}=v_{\text {local }}(r)+\sum_{l, m}\left|Y_{l m}\right\rangle \delta v_l(r)\left\langle Y_{l m}\right| \quad(58)
で与えられます.基底関数$\{\phi_j\}$に対する行列要素は,$\left\langle\phi_i\right| \hat{v}_{S L}\left|\phi_j\right\rangle$となり,基底数を$N$,角運動量の最大値を$l_{\max }$とすると, $(i, j)$の全組に対して$(l, m)$ 和を取る必要があるため,計算量・メモリ量はおよそ,$\propto N^2 l_{\max}^2$で増大し,大規模基底ではこれが非局所項の主要なボトルネックになります.そこで,非局所項を変数分離型(separable form),
v_{N L}=\sum_{l, m}\left|Q_{l m}\right\rangle A_{l m}\left\langle Q_{l m}\right| \quad(59)
で表すと,行列要素は$\left\langle\phi_i\right| \hat{v}_{N L}\left|\phi_j\right\rangle$となります.つまり各基底関数ごとに$\left\langle\phi \mid Q_{I m}\right\rangle$を作ればよくて, $N$依存のコストは,$\propto N \ell_{\max }^2$へ減少します.平面波基底のように$N$が巨大な場合,この差は決定的です.Kleinman-Bylander (KB)分離形は,semi-localの非局所項を参照擬波動関数$\psi_{l m}^{p S}$を用いて厳密に分離形へ書き換える方法で,具体的には,
\hat{v}_{ps}=v_{local}(r)+\sum_{l, m}\left|\delta v_l \psi_{l m}^{ps}\right\rangle \frac{1}{\left\langle\psi_{l m}^{ps}\right| \delta v_l\left|\psi_{l m}^{ps}\right\rangle}\left\langle\psi_{l m}^{ps} \delta v_l\right| \quad(60)
と表されます.ここで$\delta v_l=v_l-v_{local}$であり,プロジェクターを
\left|Q_{l m}\right\rangle=\left|\delta v_l \psi_{l m}^{ps}\right\rangle \quad(61)
と定義した形になっています.参照状態に対する散乱特性を保ったまま計算を軽くできる,というのがKB分離形の本質です.
Troullier–Martins (TM) 擬ポテンシャル
ここで,よく用いられているNCPPとして,Troullier–Martins (TM)擬ポテンシャルを紹介します.TM擬ポテンシャルは,平面波基底での計算効率を最大化するために「できるだけ滑らか(soft)で,しかもノルム保存条件を満たす」第一原理擬ポテンシャルを与える手法です.特に第一周期・遷移金属・希土類のように平面波収束が遅くなりがちな元素でも,少ない平面波数でも安定に計算できることを主目的としています.TM擬ポテンシャルはNCPPなので,すでに述べたHSC条件1~5あるいはその数学的条件(1)~(4)を満たします.TroullierとMartinsは,コア内$r \leq r_c$で擬波動関数を解析的かつ滑らかに表す具体的な形を与えました.彼らはコア内の擬波動関数を
R_l^{P S}(r)=r^l \exp [p(r)] \quad\left(r \leq r_c \right) \quad(62)
と置きました.これは,「原点で$r^l$で立ち上がり,硬い特異性を避け」、かつ「指数部$p(r)$を多項式にして自由度を持たせる」という設計です.彼らはさらに滑らかさを高めるため, $p(r)$は$r^2$の6次多項式(最高次は $r^{12}$)とし,
p(r)=c_0+c_2 r^2+c_4 r^4+c_6 r^6+c_8 r^8+c_{10} r^{10}+c_{12} r^{12} \quad(63)
という形を採用しました.奇数次係数を0にすることで高Fourier成分が減り,平面波収束が改善されるというのが彼らの結果です.ここで,(63)式の未知係数は7個なので,原論文では以下の7条件で一意に定めます.
1.ノルム保存条件および$r_c$で擬波動関数とその0~4階微分が連続する条件.これは結果として,遮蔽された擬ポテンシャル$V_l^{P S}(r)$とその1~2階微分の連続性を保証します.
2. 原点で擬ポテンシャルの曲率が0になる条件
V_l^{P S \prime \prime}(0)=0 \quad(64)
これが「深すぎず浅すぎない」最も滑らかなポテンシャルを選ぶ経験的に強い基準になり,実際に広いカットオフ半径の値で良い収束性を与えると示されています.
この7条件を満たす$p(r)$を得たあと,通常通り動径方向のSchrödinger(より正確にはKohn-Sham)方程式を逆に解いて遮蔽された擬ポテンシャル$V_l^{P S}(r)$を回収し,必要ならすでに述べたunscreeningによりイオン擬ポテンシャルへ変換します.これで何が嬉しいのかというと,TMの条件設定は「transferabilityを落とさずに,可能な限り大きい$r_c$を選べる」ように働きます.原論文では,同程度のtransferabilityを満たすならTMのカットオフ半径は従来のHSC/BHS/Kerker型よりかなり大きく取れると報告しています.これは平面波数を大幅に削減できることを意味し,TM擬ポテンシャルが「efficient」と呼ばれる理由です.
Vanderbiltのウルトラソフト擬ポテンシャル
TM擬ポテンシャルを含むNCPPにおいて,$2p,3d$状態は,各$l$チャネルで最も低い価電子状態で,すでに波動関数はノードを持ちません(OPW法による擬ポテンシャルで言えば,直交化させるべき内殻がないので,斥力部分が出てきません).従って,このような状態では擬ポテンシャルは浅くできないと考えられてきました.この状況を変えたのが,Vanderbiltによるウルトラソフト擬ポテンシャル(UltraSoft PseudoPotential, USPP)です.ここで言う「浅くできない」は,NCPPがカットオフ半径内のノルム保存条件を厳密に課すために,ノードのない状態では擬波動関数を十分なめらかにできず,結果として多数の平面波を要求してしまう,という問題に対応しています.VanderbiltのUSPPは,このノルム保存条件を意図的に緩めて「軟らかさ(softness)」を手に入れる手法として提案されました.
ウルトラソフト擬ポテンシャルの核心は,コア内で
\int_0^{r_c} r^2\left|R_l^{P S}(r)\right|^2 d r \neq \int_0^{r_c} r^2\left|R_l^{A E}(r)\right|^2 d r \quad(65)
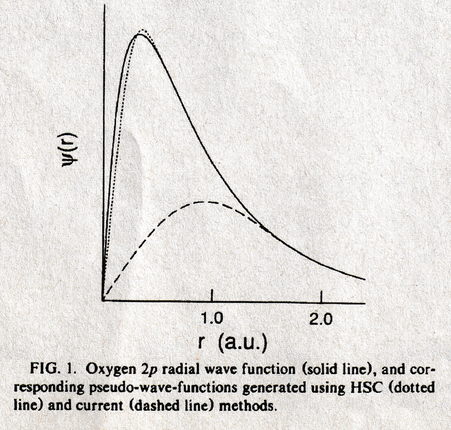
を許すことにあります.つまり「擬波動関数は全電子波動関数に比べてコア内電荷が不足してよい」ということです.その代わりに,この不足分をaugmentation charge(補償電荷)として後から補います.この自由度のおかげで,擬波動関数はノードがない状態でも大きく「滑らかにする」ことができ,従って計算に必要な平面波数を大幅に削減することができます.これが「ウルトラソフト」の意味であり,遷移金属や第一周期元素の計算を現実的なコストへ引き下げた決定打でした(ノルム保存条件の制約からの解放).下図は,酸素の2p軌道の動径方向の全電子波動関数(実線),HSC型のNCPPの擬波動関数(点線)そしてUSPPの擬波動関数(破線)の比較です.USPPの擬波動関数は,他と比べて極めて「滑らかにされて」いることがわかります.
しかし,ノルム保存条件を外すと,擬波動関数同士の内積が全電子波動関数のそれと一致しなくなります.このためUSPPでは,Kohn-Sham方程式が
\hat{H}\left|\psi_n\right\rangle=\varepsilon_n \hat{S}\left|\psi_n\right\rangle \quad(66)
という一般化固有値問題に変わってしまいます.$\hat{S}$はオーバーラップ(重なり)演算子とよばれ,補償電荷に対応する非局所項を含み,
\hat{S}=1+\sum_{i j}\left|\beta_i\right\rangle q_{i j}\left\langle\beta_j\right| \quad(67)
です.ここで$\left|\beta_i\right\rangle$がプロジェクター,$q_{i j}$がコア内ノルム差に由来するaugmentation行列です.電子密度や全エネルギーといった諸量も,通常の$|\psi|^2$に加えて補償電荷の寄与を足し込む形に修正されます.
USPPのさらなる長所として「参照エネルギーを複数取れる」という点も上げられます.VanderbiltはUSPPの枠組みで,同じ角運動量$l$に対し複数の参照エネルギー(参照状態)を選び,複数の部分波・プロジェクターを用意して散乱特性を同時に合わせ込むことができる点を強調しました.これにより,参照点近傍だけでなく広いエネルギー域で対数微分(位相シフト)が良く一致し,transferabilityが体系的に改善できます.実装としては,各$l$チャネルごとに$p=1, \ldots, P_l$のプロジェクターを持つ
\sum_{l, m} \sum_{p, p^{\prime}}\left|\beta_{l m p}\right\rangle D_{l p p^{\prime}}\left\langle\beta_{l m p^{\prime}}\right| \quad(68)
の形になり,USPPの柔らかさと多重プロジェクターのtransferability改善が「同時に」使えるのが利点です.
最後に,MBK擬ポテンシャルについても触れておきます.ここまで見てきたように,USPPの非局所形式(多重プロジェクターを含む)は非常に強力ですが,補償電荷が入るため,コード側では一般化固有値問題への対応,密度や力の補正を扱う必要があります.これに対してMorrison-Bylander-Kleinmanは,Vanderbilt の「多重参照エネルギーで散乱を合わせる」という非局所構成を保ちつつ,ノルム保存条件(正確には一般化ノルム保存条件)を再び課せることを示しました.これがMBK擬ポテンシャルです.この流れはその後,HamannのONCV(Optimized Norm-Conserving Vanderbilt)擬ポテンシャルなど「多重参照エネルギーを使う高transferability NCPP」といった手法へと発展していきます.
PAW(Projector Augmented Wave)法
ここまでで,OPW法・NCPP・USPPなどを見てきました.PAW法は,そのすべての「いいとこ取り」を狙ったような方法で,
- 全電子波動関数(AE)をきちんと再構成できる.
- しかし数値的には滑らかな擬波動関数(pseudo, soft)だけを平面波などで展開すればよい.
という線形変換として定式化されます.基本アイデアは,空間を各原子の周りの補強領域(augmentation region, R)と,それ以外(補強領域の外)に分ける. ただし,補強領域の外では擬波動関数と真の波動関数は同じとする.そして,補強領域の中だけを「修正」して全電子波動関数を「復元」する,です.
1. 補強領域と変換演算子
各原子のまわりに小さな球領域$R$を取ります(augmentation region, 補強領域といいます).この中は「内殻領域」に相当し,コアに近い部分で波動関数が激しく変化する領域です.ここで,真の全電子波動関数を$|\Psi\rangle$,それに対応する擬波動関数(滑らかな波動関数)を$|\tilde{\Psi}\rangle$と書きます.ここで,補強領域の外では,
|\tilde{\Psi}\rangle=|\Psi\rangle \quad(\mathbf{r} \notin R \text { では両者の波動関数が一致 }) \quad(69)
であり,違いがあるのは$R$の中だけとします.そこで,真の波動関数と擬波動関数を結ぶ 線形変換演算子$\hat T$を導入します.すなわち,
|\Psi\rangle = \hat T |\tilde{\Psi}\rangle \quad(70)
です.$|\tilde{\Psi}\rangle$が 補強領域$R$の中だけで$|\Psi\rangle$と異なるので,$\hat{T}$も「補強領域の中だけで効く演算子」として,
\hat{T}=1+\hat{T}_R \quad(71)
と分解できます.ここで$\hat{T}_R$は「補強領域$R$の中でのみ作用する局所的な演算子」です.以下では,この
$\hat{T}_R$の具体的な形を構成していきます(実際には,原子$a$ごとに領域$R_a$を取り,
\hat{T}=1+\sum_a \hat{T}_{R_a} \quad(72)
となりますが,ここでは簡単のために「代表的な領域$R$」として書きます).
2.部分波展開と擬部分波・全電子部分波
PAW法のキーアイデアは「補強領域の中では,波動関数を部分波の線形結合で表現する」というものです.補強領域$R$の内部で,擬波動関数$|\tilde{\Psi}\rangle$は「擬部分波(pseudo partial waves)」$\left|\tilde{\phi}_i\right\rangle$を用いて,
|\tilde{\Psi}\rangle=\sum_i\left|\tilde{\phi}_i\right\rangle c_i \quad(73)
と展開できるとします.ここでインデックス$i$は,本当は
- 原子ラベル$a$
- 主量子数・準位$n$
- 角運動量$l, m$
などの組をまとめて表していると思ってください.同様に,対応する全電子部分波(AE partial waves)を$\left|\phi_i\right\rangle$と書きます. これらは同じ量子数ラベルを持ち,「コア内では激しく振動する本物の波動関数」です.定義として,
\left|\phi_i\right\rangle=\hat{T}\left|\tilde{\phi}_i\right\rangle \quad(74)
とします.すると補強領域$R$の内部では,真の波動関数も同じ係数$c_i$を使って,
|\Psi\rangle=\sum_i\left|\phi_i\right\rangle c_i \quad(75)
と展開できます.つまり:
- $\left|\tilde{\phi}_i\right\rangle$:コア内で滑らかな「擬部分波」
- $\left|\phi_i\right\rangle$:同じチャネルに対応する「全電子部分波」
- $c_i \ldots$:どちらも同じ係数
という対応になっています.
3.全空間での$|\Psi\rangle$と$|\tilde{\Psi}\rangle$の関係
補強領域の「内側」では上の部分波展開が成り立ち,外側では$|\Psi\rangle=|\tilde{\Psi}\rangle$です.
これを全空間で一つの式で書きたいので,加減算によって整理してみます.補強領域の中では
|\tilde{\Psi}\rangle=\sum_i\left|\tilde{\phi}_i\right\rangle c_i, \quad|\Psi\rangle=\sum_i\left|\phi_i\right\rangle c_i \quad(76)
なので,全空間で
|\Psi\rangle=|\tilde{\Psi}\rangle-\sum_i\left|\tilde{\phi}_i\right\rangle c_i+\sum_i\left|\phi_i\right\rangle c_i \quad(77)
と書けます(擬波動関数から偽者(擬部分波)を引き本物(全電子部分波)を足すイメージ).外側では$\left|\tilde{\phi}_i\right\rangle$と$\left|\phi_i\right\rangle$が消えてしまう(=部分波が定義されていない)ので,この式は空間全体で有効です.あとは係数$c_i$を「$|\tilde{\Psi}\rangle$から計算できるように」したいわけです.
4.射影関数$\left|\tilde{p}_i\right\rangle$と完備性条件
そこで,係数$c_i$を,
c_i=\left\langle\tilde{p}_i \mid \tilde{\Psi}\right\rangle \quad(78)
と書けるようなプロジェクター$\left|\tilde{p}_i\right\rangle$を導入します.このとき,補強領域$R$の中では,
\sum_i\left|\tilde{\phi}_i\right\rangle\left\langle\tilde{p}_i\right|=1 \quad(\text { in } R) \quad(79)
という「局所的完備性(分解の単位元)」が必要です.そうすれば,補強領域$R$において,
\sum_i\left|\tilde{\phi}_i\right\rangle c_i=\sum_i\left|\tilde{\phi}_i\right\rangle\left\langle\tilde{p}_i \mid \tilde{\Psi}\right\rangle=\left(\sum_i\left|\tilde{\phi}_i\right\rangle\left\langle\tilde{p}_i\right|\right)|\tilde{\Psi}\rangle=|\tilde{\Psi}\rangle \quad(80)
が成り立ちます.つまり,補強領域の中で擬波動関数を部分波展開で完全に再現できるという条件です.この条件を使うと,先ほどの式
|\Psi\rangle=|\tilde{\Psi}\rangle-\sum_i\left|\tilde{\phi}_i\right\rangle c_i+\sum_i\left|\phi_i\right\rangle c_i \quad(81)
は,
\begin{aligned}
|\Psi\rangle & =|\tilde{\Psi}\rangle-\sum_i\left|\tilde{\phi}_i\right\rangle\left\langle\tilde{p}_i \mid \tilde{\Psi}\right\rangle+\sum_i\left|\phi_i\right\rangle\left\langle\tilde{p}_i \mid \tilde{\Psi}\right\rangle \\
& =|\tilde{\Psi}\rangle+\sum_i\left(\left|\phi_i\right\rangle-\left|\tilde{\phi}_i\right\rangle\right)\left\langle\tilde{p}_i \mid \tilde{\Psi}\right\rangle
\end{aligned} \quad(82)
と書き直せます.ここから,
|\Psi\rangle=\hat{T}|\tilde{\Psi}\rangle \quad(83)
という形に読み替えると,変換演算子$\hat{T}$の明示形として,
\hat{T}=1+\hat{T}_R, \quad \hat{T}_R=\sum_i\left(\left|\phi_i\right\rangle-\left|\tilde{\phi}_i\right\rangle\right)\left\langle\tilde{p}_i\right| \quad(84)
が得られます.これがPAW法の「真の波動関数と擬波動関数を結ぶ変換演算子」の本体です.実際の実装では,原子$a$ごとに,
\hat{T}=1+\sum_a \hat{T}_{R_a}, \quad \hat{T}_{R_a} =\sum_{i \in a}\left(\left|\phi_i^a\right\rangle-\left|\tilde{\phi}_i^a\right\rangle\right)\left\langle\tilde{p}_i^a\right| \quad(85)
のように書きます.ここで,$i$はその原子の部分波チャネルのラベルです.
5.演算子の変換と物理量の評価
物理量(期待値)を計算するときは,真の波動関数で$\langle\Psi| \hat{A}|\Psi\rangle$を求めたいのですが,実際に手元にあるのは擬波動関数$|\tilde{\Psi}\rangle$だけです. $|\Psi\rangle=\hat{T}|\tilde{\Psi}\rangle$ を使うと,
\langle\Psi| \hat{A}|\Psi\rangle=\langle\tilde{\Psi}| \hat{T}^{\dagger} \hat{A} \hat{T}|\tilde{\Psi}\rangle \equiv\langle\tilde{\Psi}| \tilde{A}|\tilde{\Psi}\rangle \quad(86)
と書けます.ここで,
\tilde{A}=\hat{T}^{\dagger} \hat{A} \hat{T} \quad(87)
が,擬波動関数の世界で使う「変換された演算子」です.
\hat{T}=1+\sum_i\left(\left|\phi_i\right\rangle-\left|\tilde{\phi}_i\right\rangle\right)\left\langle\tilde{p}_i\right| \quad(88)
と,
\hat{T}^{\dagger}=1+\sum_i\left|\tilde{p}_i\right\rangle\left(\left\langle\phi_i\right|-\left\langle\tilde{\phi}_i\right|\right) \quad(89)
を用いて$\tilde{A}$を展開し,補強領域内での完備性
\sum_i\left|\tilde{\phi}_i\right\rangle\left\langle\tilde{p}_i\right|=1 \quad(90)
を使って整理すると,
\tilde{A}=\hat{A}+\sum_{i, j}\left|\tilde{p}_i\right\rangle\left(\left\langle\phi_i\right| \hat{A}\left|\phi_j\right\rangle-\left\langle\tilde{\phi}_i\right| \hat{A}\left|\tilde{\phi}_j\right\rangle\right)\left\langle\tilde{p}_j\right| \quad(91)
という形になります(補強領域ごとに同様な和を取る).ポイントは,$\hat{A}$ 自身を「背景」としてそのまま残しつつ,補強領域ごとに「全電子部分波」と「擬部分波」の行列要素の差分をプロジェクター$\left|\tilde{p}_i\right\rangle$を通じて「補正」として足す,という構造になっていることです.
具体例として,
- $\hat{A}=1$ から電子密度の表式
- $\hat{A}=\hat{H}$ からエネルギーの式
- $\hat{A}=\hat{\mathbf{r}}$ から双極子モーメント
などが得られますが,すべてこの形の組み合わせで書けます.
6.OPWによる直交化との類似性
すでに述べたように,OPWでは,普通の平面波$\left|\phi_{\mathbf{k}-\mathbf{G}}\right\rangle$から「内殻状態への射影成分」を引き落として,
\chi_{\mathbf{k}, \mathbf{G}}(\mathbf{r})=\phi_{\mathbf{k}-\mathbf{G}}(\mathbf{r})-\sum_c\left[\int d^3 r^{\prime} \Phi_{c \mathbf{k}}^*\left(\mathbf{r}^{\prime}\right) \phi_{\mathbf{k}-\mathbf{G}}\left(\mathbf{r}^{\prime}\right)\right] \Phi_{c \mathbf{k}}(\mathbf{r}) \quad(92)
すなわち,
\left|\chi_{\mathbf{k}, \mathbf{G}}\right\rangle=\left(1-\sum_c\left|\Phi_c\right\rangle\left\langle\Phi_c\right|\right)\left|\phi_{\mathbf{k}-\mathbf{G}}\right\rangle \equiv \hat{T}_{\mathrm{OPW}}\left|\phi_{\mathbf{k}-\mathbf{G}}\right\rangle \quad(93)
という形で「内殻直交化済み平面波」を作りました.ここでの変換演算子は,
\hat{T}_{\mathrm{OPW}}=1-\sum_c\left|\Phi_c\right\rangle\left\langle\Phi_c\right| \quad(94)
です.これは,「内殻状態への射影を引く」ことで,価電子サブスペースだけを取り出すという,ある意味で「最も単純な線形変換」と見ることができます.一方,PAWの変換演算子は
\hat{T}=1+\sum_i\left(\left|\phi_i\right\rangle-\left|\tilde{\phi}_i\right\rangle\right)\left\langle\tilde{p}_i\right| \quad(95)
で,形はかなり複雑になっていますが,構造はよく似ています.つまり,ある基底(擬部分波)で展開された成分だけを見て,そこにだけ全電子波動関数への補正($\left|\phi_i\right\rangle-\left|\tilde{\phi}_i\right\rangle$)を加える,という意味で,OPWの「内殻直交化」を,より洗練された形に一般化したものとみなせます.
7.まとめ:PAW法の立ち位置
PAW法は,
- 全電子FP-LAPWなど:非常に正確だが高コスト
- NCPP・USPP:コアを捨てて速いが,情報を部分的に失う
という2つの方法のあいだを,線形変換$\hat{T}$によって橋渡しする枠組みです.計算は,「擬波動関数 $|\tilde{\Psi}\rangle$」上で行い,物理量は$\hat{T}$で全電子波動関数を再構成するか, $\tilde{A}=\hat{T}^{\dagger} \hat{A} \hat{T}$で演算子を変換して評価する,という流れになっています.OPW法で見た「コア状態への射影を使って不要な成分を消す」というアイデアを,部分波 $\left|\phi_i\right\rangle,\left|\tilde{\phi}_i\right\rangle$,射影演算子$\left|\tilde{p}_i\right\rangle$ - augmentation region $R$という道具立てで拡張・洗練したものがPAW法だ,というふうに並べて読むと,OPW法→擬ポテンシャル→USPP→PAW法の系譜がだいぶ見通しよく繋がると思います.
まとめ
本記事では,擬ポテンシャル法の基礎から最新の手法までを解説してきました.これまでの流れを整理すると,以下のようになります.
- 出発点(OPW法):すべての始まりはOPW法でした.原子核近傍の深いポテンシャルのせいで平面波展開の計算コストが跳ね上がる問題に対し,OPW法は「内殻準位と直交する基底」を導入することで,価電子だけを効率よく扱う道を開きました.ここから,「全電子ハミルトニアン+OPW基底」は「有効ポテンシャル+普通の平面波」と数学的に等価であるという,擬ポテンシャルの基本概念が誕生します.
- 原型から第一原理へ(AshcroftモデルとNCPP):擬ポテンシャルの原型として紹介したのが,Ashcroftの空内殻ポテンシャルです.核近傍を大胆に「空洞」と見なすモデルですが,localであることや経験的パラメータに依存するなどの問題のため,精度や移植性(transferability)に課題がありました.これを克服したのがノルム保存擬ポテンシャル(NCPP)です.全電子計算による散乱特性(位相シフト)とノルムを厳密に一致させることで,第一原理的にポテンシャルを決定します.ここでは,角運動量ごとの非局所性やKB(Kleinman-Bylander)分離形などの技術が登場し,計算効率と精度の両立が図られました.
- 非線形性の克服(NLCCとPCC):交換相関ポテンシャルの非線形性に由来する問題(単純な差分では内殻の影響を除去しきれない問題)に対しては,非線形内殻補正(NLCC)や部分内殻補正(PCC)が導入されました.これは「価電子と重なる領域の内殻効果」を適切に残すための重要な工夫です.
- 柔らかさの追求(USPP):NCPPの「ノルム保存」という制約は厳しく,特に$2p$や$3d$軌道などでは擬波動関数がどうしても「硬く(急峻に)」なりがちでした.Vanderbiltのウルトラソフト擬ポテンシャル(USPP)は,ノルム保存則をあえて緩め,不足分を補償電荷として扱うことで,極めて滑らかな擬波動関数と計算に必要な平面波の大幅な削減を実現しました.ただし代償として,一般化固有値問題やオーバーラップ演算子を扱う必要が生じます.
- 統一的枠組み(PAW法):最後に,全電子法と擬ポテンシャル法の架け橋となるPAW法を紹介しました.PAW法は「滑らかな擬波動関数で計算しつつ,必要なときは線形変換で全電子波動関数を再構成できる」強力な枠組みです.OPWの「射影による部分空間の分離」というアイデアを,より一般的かつリッチな形式で完成させたものと言えます.
それぞれの特徴を一言でまとめると,以下のようになります.
- NCPP(TM, MBK, ONCV等):理論的に素直で実装もしやすい.Transferability(移植性)も良好だが,計算に必要な平面波数がやや多い.Kohn-Sham波動関数の展開に平面波を用いず、局在した軌道を用いるAO(原子軌道)のコードでは現役で用いられている.
- USPP:非常にソフト(滑らか)で大規模計算に向く.ただし,一般化固有値問題など実装が複雑になる.
- PAW:平面波基底における現在の事実上の標準(デファクトスタンダード).全電子の情報が必要な場合や,高精度な計算に特に有利.ただし,コードが対応したい物理量(ハミルトニアン、密度、力、応力など)について,
その演算子のPAW部分波基底での行列要素(あるいはそれを構成するラジアル積分など)を,
PAWデータセット(しばしば「PAW擬ポテンシャル」という誤解を招きやすい名称が使われる)として事前に用意しておく必要がある.
いずれの手法も,「内殻の激しい構造を捨てつつ,価電子の散乱・結合の物理をどこまで忠実に残すか」という共通のテーマに対する,異なる「解」だと捉えると,擬ポテンシャルの系譜がすっきりと理解できると思います.
参考文献
[1] 寺倉清之, 尾崎泰助, JAIST SUMMER SCHOOL 2009(1日目)の資料(非公開)
ほとんどこの資料を参考にしました.
[2] R.M.マーチン 『物質の電子状態 上』シュプリンガー・ジャパン株式会社(2010)