はじめに
はじめまして。某大学の情報系学部で量子計算・量子通信を専攻している、daveと申します。
最近IBMの量子コンピュータ(シミュレータ・実機両方)に投げたjobの数が8000を超えました。
今回はあまり着目されてない、量子コンピュータの性能の話をしたいと思います。
量子コンピュータの計算方式が量子力学に基づいていて、更に素因数分解に代表されるいくつかの問題を古典コンピュータより少ない時間計算量で解けることはご存知の方も多いと思います。
現に、このQiitaでも量子アルゴリズムの解説記事がいくつか載っています。
(自分も量子コンピュータを使った量子トンネル効果のシミュレーションと連立1次方程式のための量子アルゴリズムの記事を書きましたので、良かったらご覧下さい。)
しかしこれらは全てあくまで数学・物理・CSの範疇で、性能に代表されるエンジニアリングの側面について触れた記事の存在は確認できませんでした。なので、今回は情報系大学生&普段実機で遊んでいる量子プログラマーとして、そのような話題を紹介させて頂きます。
量子コンピュータの性能指標 Quantum Volumeの概要
実機のベンチマーキング手法にRandomized Benchmarking[1]というものがあります。これは、デバイス上の量子ゲートのエラー率を取得するベンチマーク手法なのですが、実機の性能を表す指標は量子ゲートのエラー率以外だけではありません。具体的な指標やQuantum Volumeの具体的な求め方は記事内で後ほど説明します。
これらの指標全てを考慮して実機の性能を単体の数字で表す指標がQuantum Volume[2]です。
2020年8月10日現在、最大のQuantum Volumeを持つ実機はHoneywell社が6月にリリースした、Quantum Volumeが64の実機です。[3]
Quantum Volumeは何に着目しているのか
量子コンピュータの性能の評価対象として以下のものが挙げられます。
1. 使用可能な量子ビットの数
実機上で実行可能な演算の規模はまず量子ビットの数で決まります。これは、量子コンピュータ上の演算は量子ビットの上で量子ゲートを掛けた量子回路上で行われるからです。量子ビットの数が多いほどより大規模な量子回路が構成可能、つまり大規模な演算が可能であることが言えます。
2. 量子ゲートのエラー率
現段階の量子コンピュータ上の演算は物理的なノイズの影響を受けやすいので、結果が不正確になります。そのようなノイズの原因の1つに量子ゲートのエラーがあります。特に2つの量子ビットにまたがって作用する2量子ゲートのエラー率は、1量子ゲートのエラー率の10~30倍[4]あるので、より正確な演算結果を得るためには2量子ゲートを減らす必要があります。
3. 量子ビットの並び方
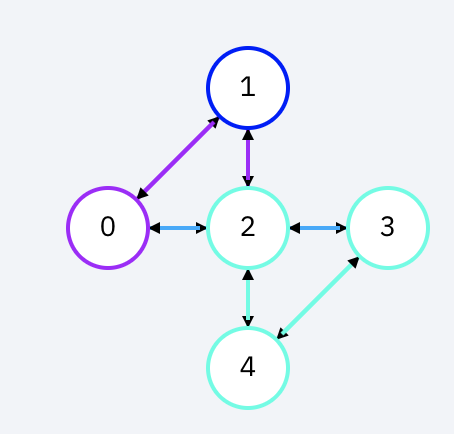
量子ビットの並び方というのは、実機によって違います。下はibmqx2(ibmq_5_yorktown)という実機の量子ビットの並び方です。(画像は[4]から引用)
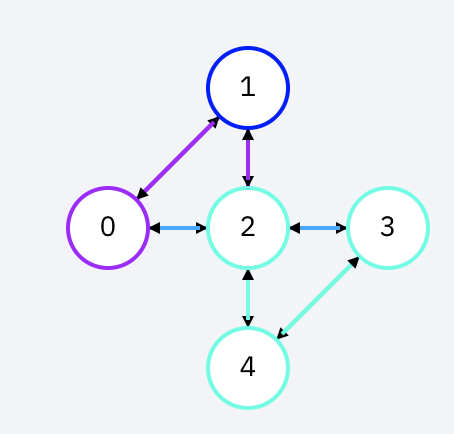
プログラムで指定された量子回路は、実機上で実行される際に量子コンパイラや量子トランスパイラによって、実機上の量子ビットの並び方に適合するように書き換えられます。
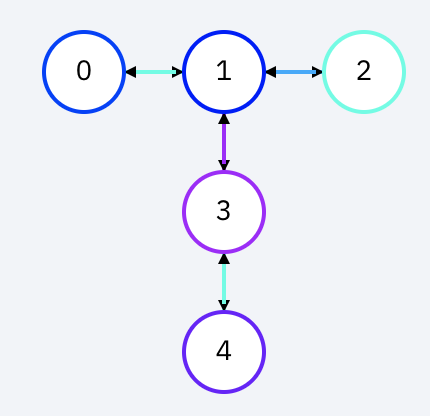
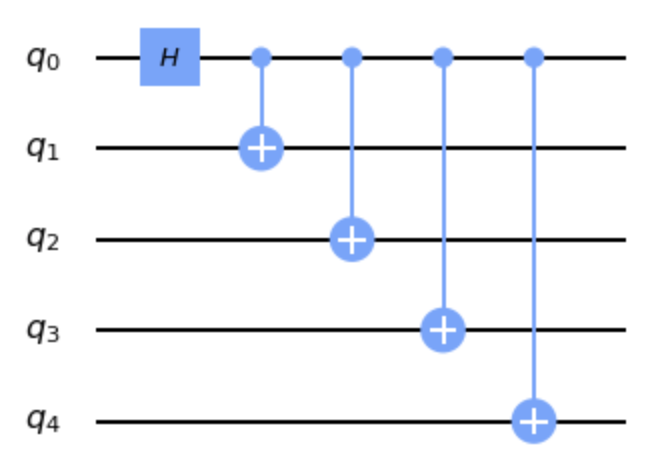
また、同じ量子ビット数を持つ複数の実機上で同じ量子回路を実装しても、実際の量子ゲート数が同じとは限りません。同じ5量子ビットを持つ2つの実機(ibmqx2, ibmq_ourence)で比較してみましょう。各実機の量子ビットの並び方は以下の画像をご覧下さい。
実機ごとのゲート数(1量子ビットゲート、CXゲート(2量子ビットゲート))は以下のようになりました。
ちなみに、これはトランスパイラの最適化レベルが3、つまり最も最適化されている場合の結果です。
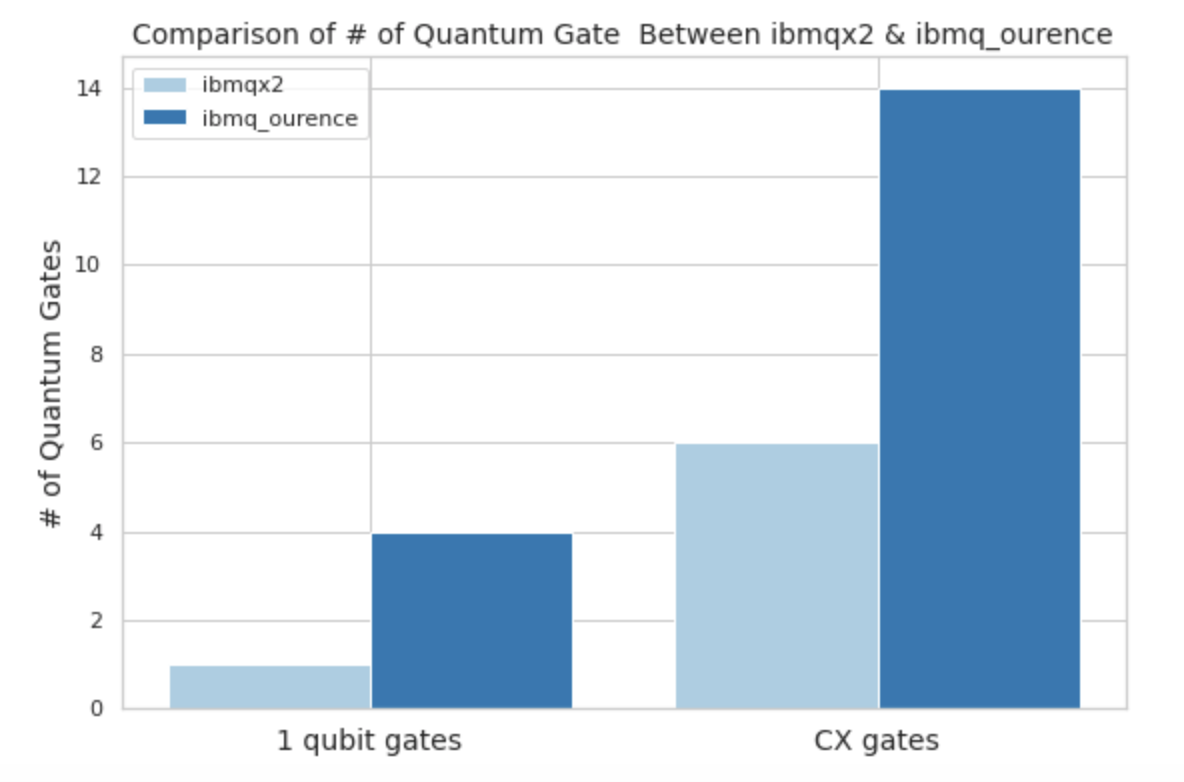
よって、量子ビット数が同じで、トランスパイラで量子回路が文字通り最適化されていたとしても、量子ビットの並び方が違えば実際の量子ゲート数が違う値になることがお分かり頂けたと思います。
4. 量子コンパイラ・トランスパイラの性能
実機上の量子ゲートを減らすためには、やはり量子コンパイラと量子トランスパイラの性能が重要になります。例えば、上述の回路をibmqx2のトランスパイラの最適化レベルを変えた結果のゲート数の変遷を表したのが以下のグラフになります。

よって、全ての最適化レベルで1量子ビットゲートの数は変わりませんが、CXゲートの数は最適化レベル2(強)と最適化レベル3(最強)で1番少なくなることが分かります。量子回路を書き換えるシステムソフトウェアの性能も、量子コンピュータの性能に深く関わっていることが分かって頂けたら嬉しいです。
Quantum Volumeの求め方
量子ビット数が$n$個の実機での実行を想定しています。
1. ランダムに2量子ビットゲートを掛ける
$m( \leq n)$個の量子ビットの範囲内で、隣り合う2つの量子ビットのペアに対して、次々とランダムな2量子ビットゲートを掛けます。(これを1depthと呼びます)
$m$が奇数の場合は、2量子ビットゲートがかからない量子ビットが存在します。
この後のステップで回路のdepthを徐々に増やしていきます。
2. 全量子ビットを観測してビット列を取得する
3. 2.で観測されたビット列のうち、heavy outputを求める
上の1.の回路Uの測定結果の確率分布$p_U(x) = |\langle x|U|0\rangle|^2$のうち、測定確率が確率分布の中央値より大きい測定結果をheavy outputと呼びます。
もっと分かりやすい形でheavy outputの集合$H_U$を表すと、
$$ H_U = [x \in [0,1]^m ,,\text{s.t.},, p_u(x) > p_{med}]$$
となります。
4. ノイズがある状態(実機)で同じ量子回路を実行する
量子回路Uを実機上でコンパイルした回路U'の測定結果の確率分布を$q_{U'}(x)$とすると、heavy outputがサンプリングできる確率は、
$$ h_U = \sum_{x \in H_U} q_{U'}(x) $$
になります。
このランダムな量子回路$U'$のdepthを増やしていき、
$$ h_1, h_2, h_3, \dots h_d(m) > \frac{2}{3}, h_{d(m)+1} \leq \frac{2}{3}$$
を満たす値$d(m)$を求めます。
5. Quantum Volumeを求める
求める値を$V_Q$とすると、
$$ \log_2{V_Q} = \text{argmax}_{m} \min(m, d(m))$$
を満たす値がその実機のQuantum Volumeの値です。
ちなみに、上の一般的な定義はランダムな量子回路の量子ビット数と最大depthは異なる値になり得ますがですが、Qiskit上の実装ではなぜか量子ビット数とdepthは同じ値だそうです。
実装
それでは、今回は実際に実機のQuantum Volumeを算出してみましょう。使う実機は先ほどご紹介した5量子ビットがあるibmqx2です。今回は実行時間短縮の都合上、実機の実行結果ではなく、qiskitが提供している実機のノイズモデルのベンチマークになります。
今回のコードはQiskit Tutorialのコード[5]を大幅に改変したものです。
"""
This is the drastically-modified form of © Copyright IBM 2017, 2020.
"""
# ライブラリをインポートする
import numpy as np
import matplotlib.pyplot as plt
from IPython import display
from qiskit import QuantumCircuit, Aer, execute
from qiskit.compiler import transpile
from qiskit.providers.aer.noise import NoiseModel
from qiskit.providers.aer.noise.errors.standard_errors import depolarizing_error, thermal_relaxation_error
from qiskit.test.mock import FakeYorktown
import qiskit.ignis.verification.quantum_volume as qv
# あれば
# from qiskit import IBMQ
# token = 'Replace me'
# IBMQ.enable_account(token)
# provider = IBMQ.get_provider(group='Replace me')
# 実験に使う量子ビットのインデックス
qubit_lists = [[3, 4, 2], [3, 4, 2, 0], [3, 4, 2, 0, 1]]
# 実験回数
num_experiments = 100
# ランダムな量子回路を構築
qv_circs, qv_circs_nomeas = qv.qv_circuits(qubit_lists, num_experiments)
# ノイズがない状況で実験
ideal_results = []
for trial in range(num_experiments):
job = execute(qv_circs_nomeas[trial],
backend=Aer.get_backend('statevector_simulator'))
result = job.result()
ideal_results.append(result)
print('Simulating trial %d'%trial)
# ノイズがない環境の状態ベクトルをfitterに追加
qv_fitter = qv.QVFitter(qubit_lists=qubit_lists)
qv_fitter.add_statevectors(ideal_results)
# ノイズがある状況で実験
backend = Aer.get_backend('ibmqx2')
experiment_results = []
for trial in range(num_experiments):
print('Running trial %d'%trial)
job = execute(qv_circs[trial],
backend = Aer.get_backend("qasm_simulator"),
basis_gates = basis_gates = backend.configuration().basis_gates,
coupling_map = backend.configuration().coupling_map,
noise_model = NoiseModel.from_backend(backend),
optimization_level = 3,
shots = 8192)
result = job.result()
exp_results.append(result)
# ノイズがある環境の実験結果をfitterに追加
qv_fitter.add_data(experiment_results)
# Heavy probabilityの変化をプロット
plt.figure(figsize=(10, 6))
ax = plt.gca()
qv_fitter.plot_qv_data(ax=ax, show_plt=False)
ax.set_title('Quantum Volume of ibmqx2', fontsize=20)
plt.show()

# Quantum Volumeを計算
qv_success_list = qv_fitter.qv_success()
qv_list = qv_fitter.ydata
for qidx, qubit_list in enumerate(qubit_lists):
if qv_list[0][qidx]>2/3:
if qv_success_list[qidx][0]:
print("Width/depth %d greater than 2/3 (%f) with confidence %f (successful). Quantum volume %d"%
(len(qubit_list),qv_list[0][qidx],qv_success_list[qidx][1],qv_fitter.quantum_volume()[qidx]))
else:
print("Width/depth %d greater than 2/3 (%f) with confidence %f (unsuccessful)."%
(len(qubit_list),qv_list[0][qidx],qv_success_list[qidx][1]))
else:
print("Width/depth %d less than 2/3 (unsuccessful)."%len(qubit_list))
Width/depth 3 greater than 2/3 (0.791626) with confidence 0.998954 (successful). Quantum volume 8
Width/depth 4 greater than 2/3 (0.708406) with confidence 0.820785 (unsuccessful).
Width/depth 5 greater than 2/3 (0.695206) with confidence 0.732370 (unsuccessful).
よって、ibmqx2のQuantum Volumeは8(なのではないか)ということが分かりました。
皆さんも他の実機(のノイズモデル)でやってみて下さい!
参考文献
[1]The World’s Highest Performing Quantum Computer is Here
https://www.honeywell.com/en-us/newsroom/news/2020/06/the-worlds-highest-performing-quantum-computer-is-here
[2]Easwar Magesan, J. M. Gambetta, and Joseph Emerson, Robust randomized benchmarking of quantum processes, https://arxiv.org/pdf/1009.3639
[3]Cross, Andrew W., et al. "Validating quantum computers using randomized model circuits." Physical Review A 100.3 (2019): 032328.
https://arxiv.org/pdf/1811.12926.pdf
[4]IBM Quantum Experience
https://quantum-computing.ibm.com
[5] Quantum Volume — Qiskit 0.19.6 documentation © Copyright IBM 2017, 2020.
https://qiskit.org/documentation/tutorials/noise/5_quantum_volume.html