Rでガウス・ニュートン法とレーベンバーグ・マーカート法を実装

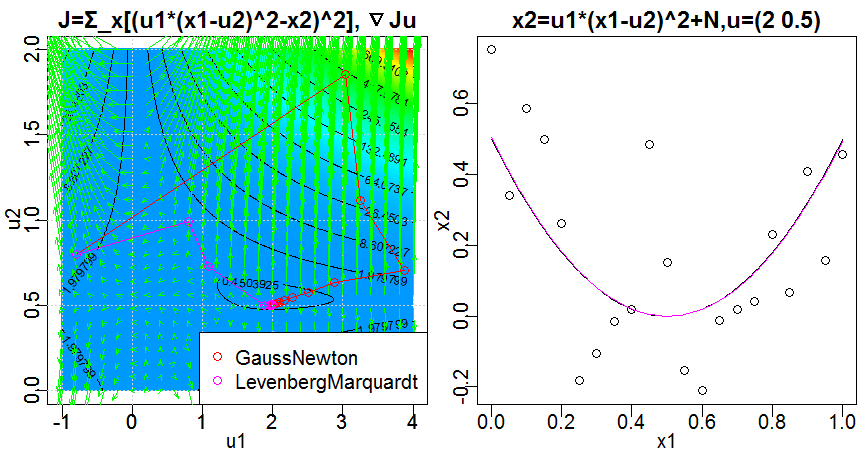
これなら分かる最適化数学 4.3.1 に記載の通り、ガウス・ニュートン法を用いて、非線形最小二乗法の誤差関数

J(\mathbf{u})=\frac{1}{2}\sum_{\alpha=1}^N \sum_{l=1}^r F_l(\mathbf{x}_\alpha,\mathbf{u})^2

に最小値を取らせる変数$\mathbf{u}$の値を求めます。

この例では、観測した点$\mathbf{x}\alpha=(x{\alpha1},x_{\alpha2})^T , \alpha=1,\dots,N$に対して関数$x_2=u_1*(x_1-u_2)^2$を当てはめるとき、誤差関数を最小にするようなパラメータ$\mathbf{u}=(u_1,u_2)^T$を求める問題を想定し、$r=1$, $F_1(\mathbf{x},\mathbf{u})=u_1*(x_1-u_2)^2-x_2$としています。なお、$\mathbf{x}\alpha$を生成する際には、正規分布に従うノイズを加え、$x{\alpha2}=u_1*(x_{\alpha1}-u_2)^2+N(0,\sigma^2),\mathbf{u}=(2,0.5)^T$としています。

また、4.3.2に記載の通り、レーベンバーグ・マーカート法を用いて、同じ問題を解きます。更新式は

\mathbf{u}^{(K+1)}=\mathbf{u}^{(K)}-(\mathbf{H_u}^{(K)}+cD[\mathbf{H_u}])^{-1}\nabla_\mathbf{u}J^{(K)}

としていますが、if文による切り替えで、

\mathbf{u}^{(K+1)}=\mathbf{u}^{(K)}-(\mathbf{H_u}^{(K)}+c\mathbf{I})^{-1}\nabla_\mathbf{u}J^{(K)}

とすることもできます。

library(pracma)

# Taken and modified from: http://cran.r-project.org/web/packages/pracma/index.html
vectorfield <- function(fun, xlim, ylim, n = 16,
                        scale = 0.05, col = "green", ...) {
    stopifnot(is.numeric(xlim), length(xlim) == 2,
              is.numeric(ylim), length(ylim) == 2)

    xpts <- linspace(xlim[1], xlim[2], n)
    ypts <- linspace(ylim[1], ylim[2], n)

    M <- meshgrid(xpts, ypts)
    x <- M$X
    y <- M$Y

    f <- fun(x, y)
    stopifnot(nrow(f) <= 2)
    if (nrow(f) == 1) {
        px = matrix(1, nrow=n , ncol=n)
        py = fun(x, y);
    } else {
        px = matrix(f[1, ], nrow=n , ncol=n)
        py = matrix(f[2, ], nrow=n , ncol=n)
    }

    plot(xlim, ylim, type="n", xlab = "", ylab = ""); grid()
    quiver(x, y, px, py, scale = scale, col = col, ...)
}

# Taken and modified from: http://cran.r-project.org/web/packages/pracma/index.html
quiver <- function(x, y, u, v,
                    scale = 0.05, angle = 10, length = 0.1, ...) {
    stopifnot(is.numeric(x), is.numeric(y), is.numeric(u), is.numeric(v))

    arrows(x, y, x+scale*u, y+scale*v, angle=angle, length=length, ...)
}

frame()
set.seed(0)
par(mfrow=c(1, 2))
par(mar=c(2, 2, 1.5, 0.1))
par(mgp=c(1, 0.2, 0))
u1 <- seq(-1, 4, 0.01)
u2 <- seq(0, 2, 0.01)
x1 <- seq(0, 1, 0.05)
x2 <- 2 * (x1 - 0.5) ^ 2 + rnorm(length(x1), 0, 0.2)
f <- function(x1, x2, u) { u[1] * (x1 - u[2]) ^ 2 - x2 }
du1 <- function(x1, u) { (x1 - u[2]) ^ 2 }
du2 <- function(x1, u) { -2 * u[1] * (x1 - u[2]) }
u0 <- c(-0.8, 0.8)

gaussnewton <- function(u0, f, du1, du2) {

    u <- as.matrix(u0)
    eps <- 1e-12
    i <- 1
    repeat {
        oldu <- u
        # 勾配∇Jを求める。
        gradientj <- rowSums(f(x1, x2, u) * rbind(du1(x1, u), du2(x1, u)))
        # ヘッセ行列のガウスニュートン近似Hを求める。
        H <- matrix(rowSums((sapply(x1, function(x1) {
            c(du1(x1, u), du2(x1, u)) %*% t(c(du1(x1, u), du2(x1, u)))
        }))), nrow=length(u))
        # HΔu=-∇Jを解き、Δu=-H^-1 ∇Jを求める。
        deltau <- solve(H, -gradientj)
        u <- u + deltau
        xy <- cbind(oldu, u)
        lines(xy[1, ], xy[2, ], type="o", col=2)
        cat("i=", i, "gradientj=", gradientj, "u=" , u, "\n")
        # ||Δu||^2 が十分小さくなるまで繰り返す。
        if (sum(deltau * deltau) < eps) {
            break
        }
        i <- i + 1
    }
    u
}

levenbergmarquardt <- function(u0, f, du1, du2) {

    c <- 0.0001
    u <- as.matrix(u0)
    eps <- 1e-12
    i <- 0
    repeat {
        oldu <- u
        j <- 1 / 2 * sum(f(x1, x2, u)^2)
        # 勾配∇Jを求める。
        gradientj <- rowSums(f(x1, x2, u) * rbind(du1(x1, u), du2(x1, u)))
        # ヘッセ行列のガウスニュートン近似Hを求める。
        H <- matrix(rowSums((sapply(x1, function(x1) {
            c(du1(x1, u), du2(x1, u)) %*% t(c(du1(x1, u), du2(x1, u)))
        }))), nrow=length(u))
        repeat {
            if (T) {
                # (H+cD[H])Δu=-∇Jを解き、Δu=-(H+cD[H])^-1 ∇Jを求める。
                deltau <- solve(H + c * diag(diag(H)), -gradientj)
            } else {
                # (H+cI)Δu=-∇Jを解き、Δu=-(H+cI)^-1 ∇Jを求める。
                deltau <- solve(H + c * diag(length(u)), -gradientj)
            }
            newu <- u + deltau
            newj <- 1 / 2 * sum(f(x1, x2, newu)^2)
            # 解から離れてしまったときはcを大きくしてガウスニュートン法の影響を弱め、
            # Δuを求め直す。
            if (newj <= j) {
                break
            }
            cat("newj=", newj, "j=", j, "c=", c, "\n")
            c <- c * 10
        }
        # 解に近づくにつれ、cを小さくしてガウスニュートン法の影響を強める。
        u <- u + deltau
        c <- c / 10
        i <- i + 1
        xy <- cbind(oldu, u)
        lines(xy[1, ], xy[2, ], type="o", col=6)
        cat("i=", i, "gradientj=", gradientj, "u=" , u, "c=", c, "\n")
        # ||Δu||^2 が十分小さくなるまで繰り返す。
        if (sum(deltau * deltau) < eps) {
            break
        }
    }
    u
}

j <- outer(u1, u2, Vectorize(function(u1, u2) { 1 / 2 * sum(f(x1, x2, c(u1, u2))^2) }))
contour(u1, u2, j, xlab="u1", ylab="u2", main="J=Σ_x[(u1*(x1-u2)^2-x2)^2], ∇Ju")
image(u1, u2, j, col=rainbow(450)[256:1], add=T)
contour(u1, u2, j, xlab="", ylab="", levels=range(j)[1] + abs(diff(range(j))) * seq(0, 1, 0.1) ^ 4, add=T)
v <- Vectorize(function(u1, u2) {
    as.vector(rowSums(f(x1, x2, c(u1, u2)) * rbind(du1(x1, c(u1, u2)), du2(x1, c(u1, u2)))))
    })
par(new=T)
vectorfield(v, range(u1), range(u2), n=26, angle=20, length=0.05)
# l <- locator(1); u0 <- c(l$x, l$y)
ugn <- gaussnewton(u0, f, du1, du2)
ulm <- levenbergmarquardt(u0, f, du1, du2)
legend("bottomright", legend=c(
    "GaussNewton", 
    "LevenbergMarquardt"), 
    col=c(2, 6), pch=1, bg="white")

plot(x1, x2, main="x2=u1*(x1-u2)^2+N,u=(2 0.5)")
s <- function(x){ 2 * (x - 0.5) ^ 2 }
curve(s, col=1, add=T)
fitted <- function(x){ ugn[1] * (x - ugn[2]) ^ 2 }
curve(fitted, col=2, add=T)
fitted <- function(x){ ulm[1] * (x - ulm[2]) ^ 2 }
curve(fitted, col=6, add=T)