Rでガウス分布の平均パラメータを逐次最尤推定

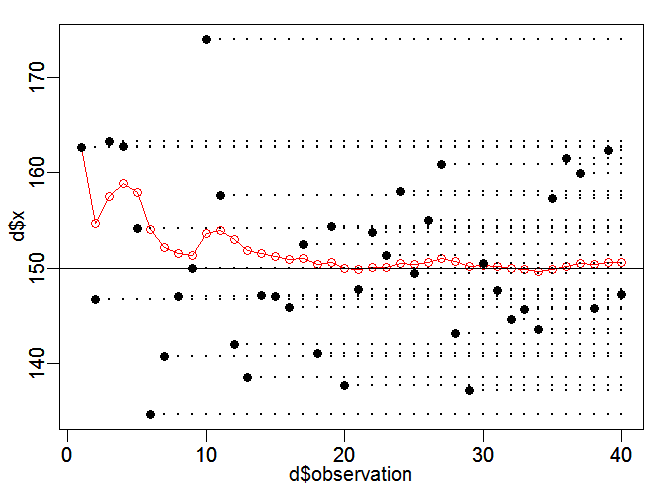
PRML 2.3.5に記載の通り、ガウス分布の平均パラメータuの最尤推定に関して、対数尤度の微分が0となるuを求める問題を、確率変数uが与えられた時の確率変数z=-d/du [ln p(x|u,σ^2)]の条件付き期待値E[z|u]が0となるuを求める問題に帰着し、Robbins-Monroアルゴリズムにより、xの観測（すなわちzの観測）毎に、そのようなuを逐次的に求めます。

サンプルはガウス分布から生成し、観測した点を黒点、逐次推定したパラメータuを赤点で示します。

frame()
set.seed(0)
par(mfrow=c(1, 1))
par(mar=c(2.3, 2.5, 1, 0.1))
par(mgp=c(1.3, .5, 0))
N <- 40
U <- 150
x <- rnorm(N, U, 10)
uml <- 0
umls <- numeric()
d <- data.frame(observation=-1, x=NA, new=F)
for (n in 1:N) {
    uml <- uml + (1 / n) * (x[n] - uml)
    umls <- c(umls, uml)
    if (n > 1) {
        previous <- d[d$observation == n - 1, ]
        previous$observation = n
        previous$new = F
        d <- rbind(d, previous)
    }
    d <- rbind(d, c(n, x[n], T))
}
d <- d[-1, ]
plot(umls, type="o", col=2, xlim=c(1,N), ylim=c(min(x), max(x)), xlab="", ylab="")
par(new=T)
plot(d$observation, d$x, pch=19, cex=ifelse(d$new, 1, 0.1), xlim=c(1,N), ylim=c(min(x), max(x)))
abline(h=U)