Rで共役勾配法を実装

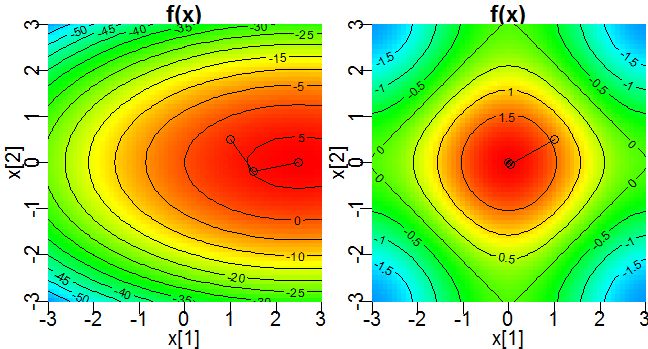
これなら分かる最適化数学 3.3 に記載の通り、共役勾配法を用いて、関数に最大値・最小値を取らせる変数の値を求めます。以下の例では最大値を取る点を求めています。

なお、探索直線は、前回の探索直線の方向とヘッセ行列に関して共役な方向を向いています。if文による切り替えで、Polak-Ribiereの式による近似を用いた方向を向かせることもできます。

また、探索直線上では、与えられた関数に対して通常の勾配法による探索を行っています。例題3.5のように、2次近似を用いて解析的に探索直線上の解を求めることはしていません。

frame()
par(mfcol=c(1, 2))
par(mar=c(2, 2, 1, 0.1))
par(mgp=c(1, 0.2, 0))

search <- function(x0, delta, f, df) {
	
	x <- x0
	h <- 0.7
	eps <- 1e-6
	i <- 1
	# 解の移動量が十分小さくなるまで繰り返す。
	repeat {
		oldx <- x
		# df(x)の符号によって、進む方向を決める。
		h <- sign(df(x)) * abs(h)
		newx <- x + h * delta
		if (f(x) < f(newx)) {
			# 関数値が増大する限り、ステップ幅を倍にしていく。
			repeat {
				h <- 2 * h
				x <- newx
				newx <- x + h * delta
				if (f(x) >= f(newx)) {
					break
				}
			}
			h <- h / 2
		} else {
			# 関数値が減少してしまうときは、ステップ幅を半分にしていき、
			# 関数値が増大する位置を見つける。
			repeat {
				h <- h / 2
				newx <- x + h * delta
				if (f(x) <= f(newx)) {
					break
				}
			}
			x <- newx
			h <- 2 * h
		}
		cat("search i=", i, "x=" , x, "f(x)=", f(x), "df(x)=", df(x), "h=", h, "\n")
		if (abs(h) < eps) {
			break
		}
		i <- i + 1
	}
	x
}

conjugatedescent <- function(x0, f, df, dxdx, dxdy, dydx, dydy) {
	
	x <- x0
	eps <- 1e-12
	i <- 1
	m <- rep(0, length(x0))
	repeat {
		oldx <- x
		oldm <- m
		# 勾配∇fを求める。
		gradientf <- c(dx(x), dy(x))
		# 共役勾配mを求める。
		if (i == 1) {
			# 最初は∇fの方向に探索する。
			alpha <- 0
		} else {
			if (T) {
				# alphaの定義通りヘッセ行列を使用
				H <- matrix(c(dxdx(x), dxdy(x), dydx(x), dydy(x)), 2, byrow=T)
				alpha <- -(oldm %*% (H %*% gradientf)) / (oldm %*% (H %*% oldm))
			} else {
				# alphaをPolak-Ribiereの式で近似
				alpha <- (gradientf %*% (gradientf - oldgradientf)) / (oldgradientf %*% oldgradientf)
			}
		}
		m <- gradientf + alpha * oldm
		cat("conjugatedescent i=", i, "x=" , x, "f(x)=", f(x), "m=", m, "\n")
		# 探索直線上の関数F(t)=f(x(t))について、1階微分dF/dt=∇f^T * ∇mを求める。
		df <- function(x) { as.numeric(c(dx(x), dy(x)) %*% m) }
		# 探索直線の方向ベクトルを正規化する。
		delta <- scale(m, center=F)
		# 直線探索する。
		x <- search(x, delta, f, df)
		# 軌跡を描画する。
		xy <- cbind(oldx, x)
		lines(xy[1, ], xy[2, ], type="o", col=1)
		diff = x - oldx
		# ||Δx||^2 が十分小さくなるまで繰り返す。
		if (sum(diff * diff) < eps) {
			break
		}
		oldgradientf <- gradientf
		i <- i + 1
	}
	x
}

draw <- function() {
	xgrid <- seq(-3, 3, 0.1)
	ygrid <- seq(-3, 3, 0.1)
	zgrid <- outer(xgrid, ygrid, Vectorize(function(x, y){ f(c(x, y)) }))
	image(xgrid, ygrid, zgrid, xlim=range(xgrid), ylim=range(ygrid), xlab="x[1]", ylab="x[2]", main="f(x)", col=rainbow(450)[256:1])
	contour(xgrid, ygrid, zgrid, xlim=range(xgrid), ylim=range(ygrid), add=T)
	conjugatedescent(c(1, 0.5), f, dx, dxdx, dxdy, dydx, dydy)
}

f <- function(x){ -x[1] ^ 2 - 4 * x[2] ^ 2 + 5 * x[1] }
dx <- function(x){ -2 * x[1] + 5 }
dy <- function(x){ - 8 * x[2] }
dxdx <- function(x){ -2 }
dxdy <- function(x){ 0 }
dydx <- function(x){ 0 }
dydy <- function(x){ -8 }
draw()

f <- function(x){ cos(x[1]) + cos(x[2]) }
dx <- function(x){ -sin(x[1]) }
dy <- function(x){ -sin(x[2]) }
dxdx <- function(x){ -cos(x[1]) }
dxdy <- function(x){ 0 }
dydx <- function(x){ 0 }
dydy <- function(x){ -cos(x[2]) }
draw()

# f <- function(x){ -(x[1] ^ 3 + x[2] ^ 3 - 9 * x[1] * x[2] + 27) }
# dx <- function(x){ -(3 * x[1] ^ 2 - 9 * x[2]) }
# dy <- function(x){ -(3 * x[2] ^ 2 - 9 * x[1]) }
# dxdx <- function(x){ -6 * x[1] }
# dxdy <- function(x){ 9 }
# dydx <- function(x){ 9 }
# dydy <- function(x){ -6 * x[2] }
# draw()