Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@daris755

セグ木のお勉強

Posted at

セグ木

1点更新、区間積の取得ができます。

説明

原理などいろいろのパートです。

イメージ

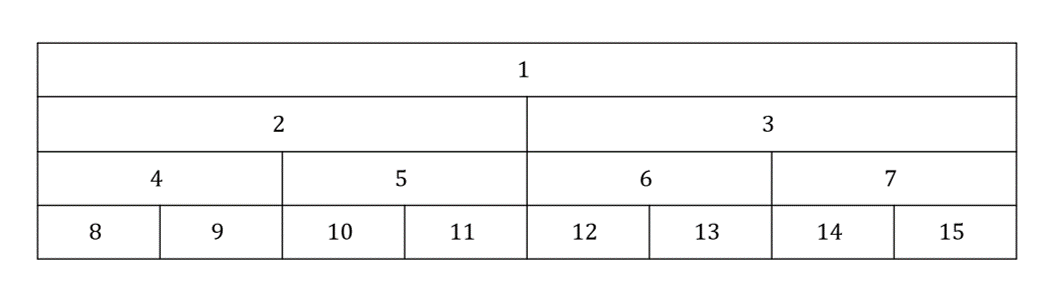
大きさ$n$の配列$a$に対してのセグ木を考えます。$n=8$として、和でイメージすると次のようになります。隣同士の和を下から積み上げているように見えると嬉しいです。

セグ木.png

これに対して添え字をつけます(1-based index)。

画像2.png

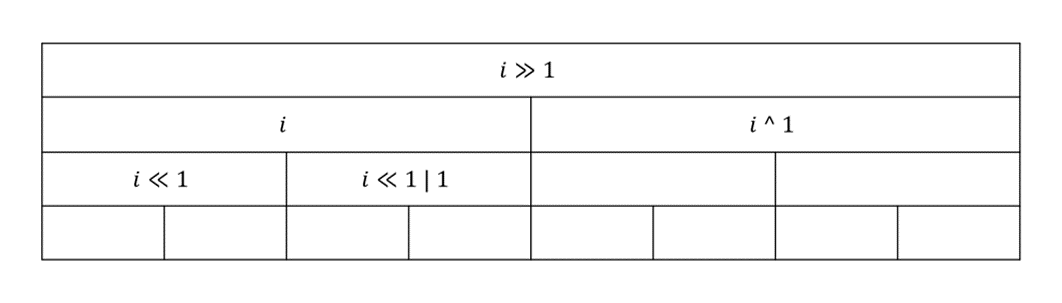
親、子、兄弟の要素へのアクセスは次のようにできます。

画像3.png

抽象化

和を例に挙げましたが、モノイドなら何でもセグ木にのります。つまり

  • 演算$*$について$a * ( b * c ) = (a * b) * c$
  • $e * a = a * e = a$満たす$e$が存在する（このような$e$を単位元という）

の2つを満たしていればいいです（もっと厳密な書き方はすごい人がすればいいと思います）。コード上では$a * b$は関数$f(a, b)$で表されます。

実装

中身はほぼACLと同じです。二分探索まで書きます。

方針

  • 1-based index
  • 非再帰
  • $n = 2^k$でなくてよい

ひな形

template <typename T>
class SegmentTree {
   private:
    using F = function<T(T, T)>;
    
    int n;
    vector<T> seg;
    const F f;
    const T e;
    
   public:
};

publicにいろいろ追加していきます。最後に全部まとめたものを貼っておきます。

コンストラクタ

constructor
SegmentTree(int n, const F f, const T& e) : n(n), seg(vector<T>(2 * n, e)), f(f), e(e) {}

SegmentTree(const vector<T>& v, const F f, const T& e) : n(v.size()), seg(2 * n), f(f), e(e) {
    for (int i = 0; i < n; i++) {
        seg[n + i] = v[i];
    }
    for (int i = n - 1; i >= 1; i--) {
        seg[i] = f(seg[i << 1], seg[i << 1 | 1]);
    }
}

一つ目は単位元で初期化してるだけです。
二つ目は最初に説明した図を参考にすると

  • 元の配列の各データが$seg$の$[n, 2n)$の部分にそれぞれ入る
  • $seg[i]$は$seg[2i]$と$seg[2i + 1]$の積（後ろから計算）

であることが分かります。$seg[0]$は使いません。

例えば区間和をとりたいときは

区間和
SegmentTree<int> seg(n, [](int a, int b) { return a + b; }, 0);

区間のminをとりたいときは

区間min
SegmentTree<int> seg(n, [](int a, int b) { return min(a, b); }, 1 << 30);

のように呼び出せます。

１点取得

T operator[](const int i) const { return seg[i + n]; }

元の配列と$seg$の添え字の対応を実装しておいた方が便利です。

１点更新

update
void update(int i, const T& x) {
    i += n;
    seg[i] = x;
    while (i > 1) {
        i >>= 1;
        seg[i] = f(seg[i << 1], seg[i << 1 | 1]);
    }
}

下から上に更新していきます。添え字を元の配列と対応させた後（2行目）に2で割っていけばよいです。

画像4.png

区間取得

query
T query(int l, int r) {
    l += n;
    r += n;
    T l_val = e;
    T r_val = e;
    while (l < r) {
        if (l & 1) {
            l_val = f(l_val, seg[l]);
            l++;
        }
        if (r & 1) {
            r--;
            r_val = f(seg[r], r_val);
        }
        l >>= 1;
        r >>= 1;
    }
    return f(l_val, r_val);
}
  • なるべくセグ木の上の部分を使いたい
  • 非可換でも成り立つことを意識する
  • まず$l,r$に$n$を足して$seg$での位置と対応させる
  • $l$が奇数のときは右の子が、$r - 1$が偶数のときは左の子が対応しているので、それぞれその場で計算する。そうでないときは親に任せる

例えば$[l, r) = [0, 7)$として、セグ木上の添え字に直して$[l, r) = [8, 15)$から始めます。

$[l, r) = [8, 15), l\_val = 0, r\_val = 0$
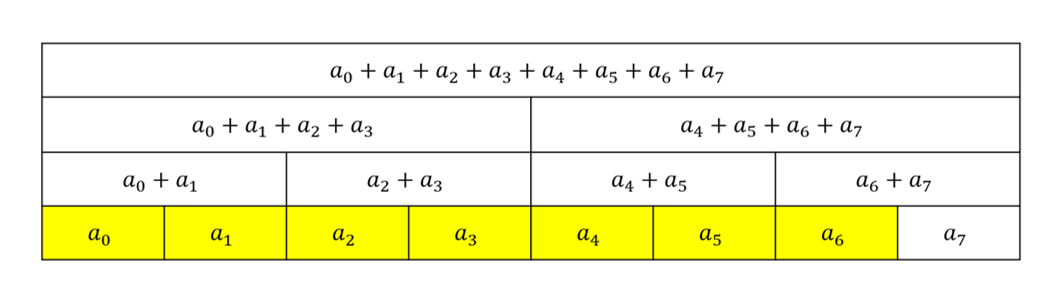
画像5.png

$[l, r) = [4, 7), l\_val = 0, r\_val = a_6$
画像6.png

$[l, r) = [2, 3), l\_val = 0, r\_val = (a_4 + a_5) + a_6$
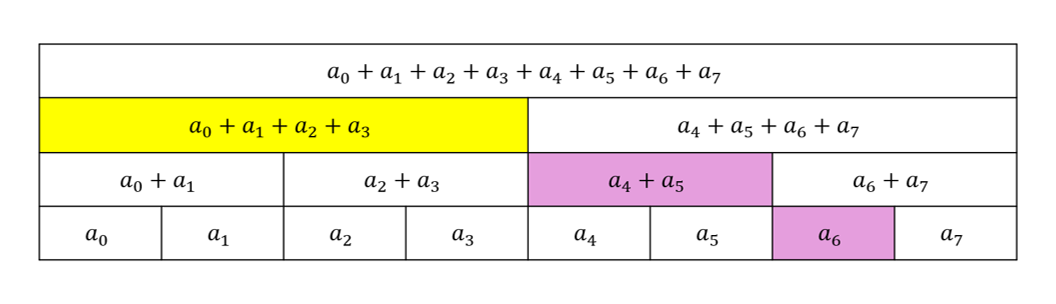
画像7.png

$[l, r) = [1, 1), l\_val = a_0 + a_1 + a_2 + a_3, r\_val = a_4 + a_5 + a_6$
画像8.png

$[l, r) = [1, 1)$で空になったので、$l\_val + r\_val = a_0 + a_1 + a_2 + a_3 + a_4 + a_5 + a_6$が求める値です。

nが2冪でないときのおはなし

今まで説明に用いた図は$n=8$で$n$が2冪であるものでしたが、そうでないときもちゃんと動くよーというのを書きます。

$n=9$で図示すると次の通りです（右上は添え字）。
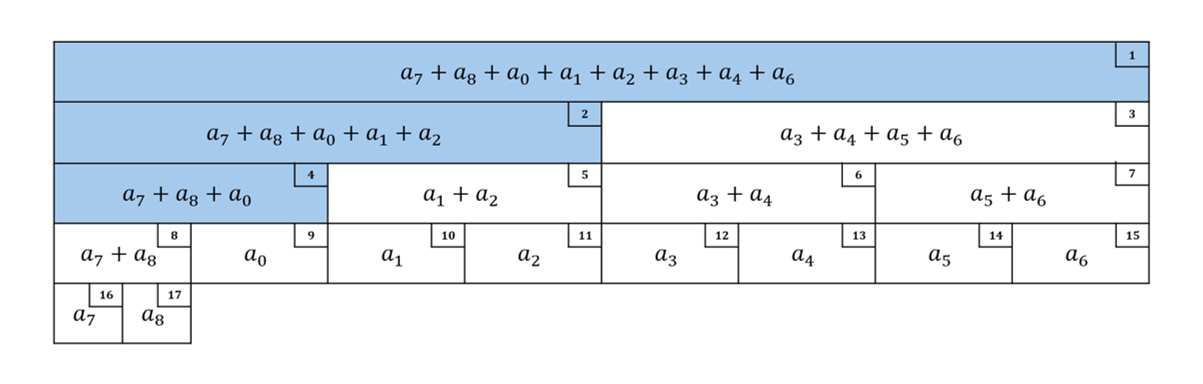
画像9.png
$seg[i] = seg[2i] + seg[2i + 1]$となるように作りましたが、青い部分には使えない値が入っています。

個人的には下の方が好きです。
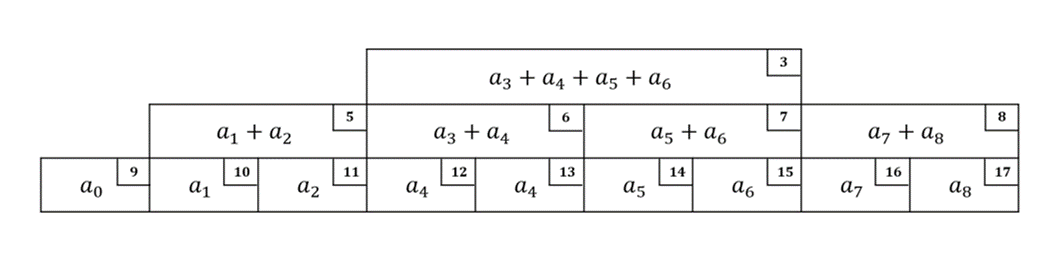
画像10.png
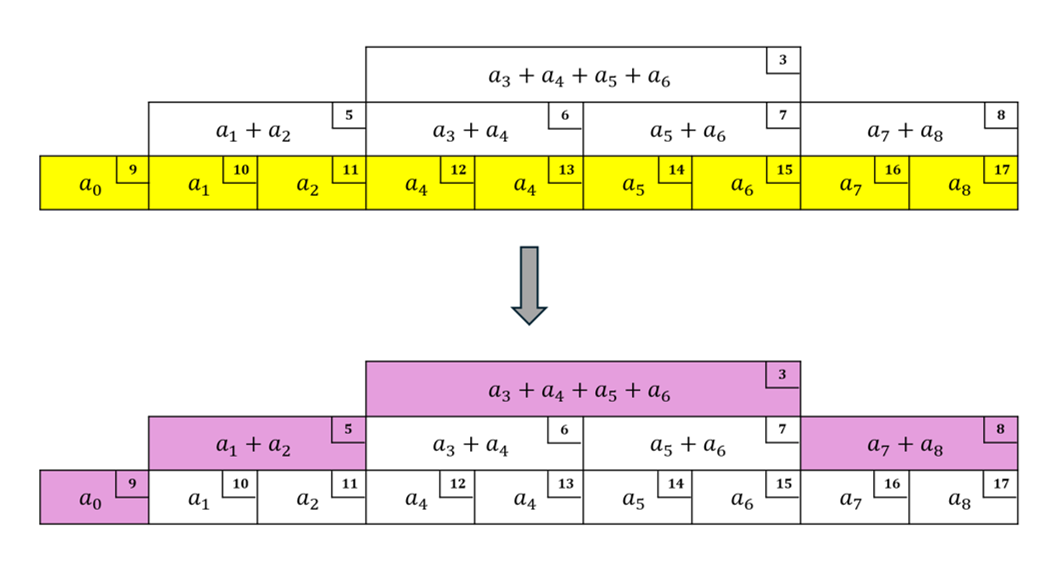
区間取得の挙動を思い出すと、$l < r$を保ったまま区間を狭めていくことや、左右の子が正常な値である親ももまた正常な値をもつことから、使えない値の部分にアクセスすることはなく正常に動きます。
画像11.png

二分探索

max_right
template <class S>
int max_right(int l, S check) const { // max(r) s.t. check(query(l, r)) = true
    assert(0 <= l && l <= n);
    int r = l;
    l += n;
    int w = 1;
    T l_val = e;
    for (; r + w <= n; l >>= 1, w <<= 1) {
        if (l & 1) {
            if (check(f(l_val, seg[l]))) {
                l_val = f(l_val, seg[l]);
                r += w;
                l++;
            } else {
                break;
            }
        }
    }
    for (; w > 0; l <<= 1, w >>= 1) {
        if (r + w <= n && check(f(l_val, seg[l]))) {
            l_val = f(l_val, seg[l]);
            r += w;
            l++;
        }
    }
    return r;
}
  • $check$を満たす$query(l, r)$のうち最大の$r$を返す（$l$は固定）
  • 1個目のループで最下段から上までのぼる
  • 左の子なら親に委ねる
  • 右の子なら条件を満たしているか確認
  • 2個目のループで降りていく
  • $w$は現在見ている部分の幅

詳しくは例を見ます。これまで通り累積和で考えると、例えば$a_i \geq 0$を仮定すれば二分探索ができます。$[l, r)$の和が$x$未満となる最大の$r$を見つけてみましょう。$n = 9、l = 0, x = 24$とします。

int n;
cin >> n;
vector<int> a(n);
for (auto& aa: a) cin >> aa;
SegmentTree<int> seg(a, [](int x, int y) { return x + y; }, 0);
int x;
cin >> x;
cout << seg.max_right(0, [&](int y) { return y < x; });
input
9
3 1 4 1 5 9 2 6 5
24

右の子なのでその場で確認：$r = 0, w = 1, l\_val = 0$
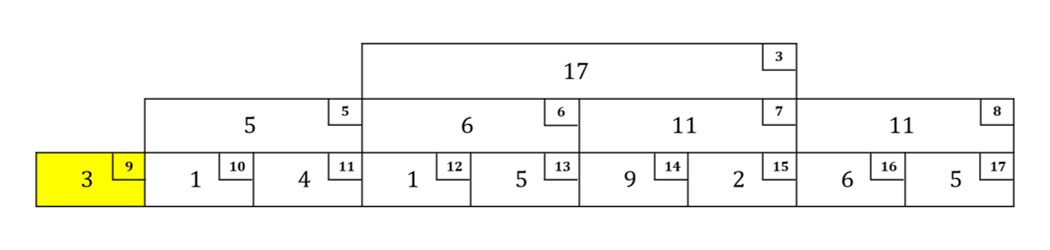
画像12.png
条件を満たすのでのぼり、次の部分も右の子なのでその場で確認：$r = 1, w = 2, l\_val = 3$
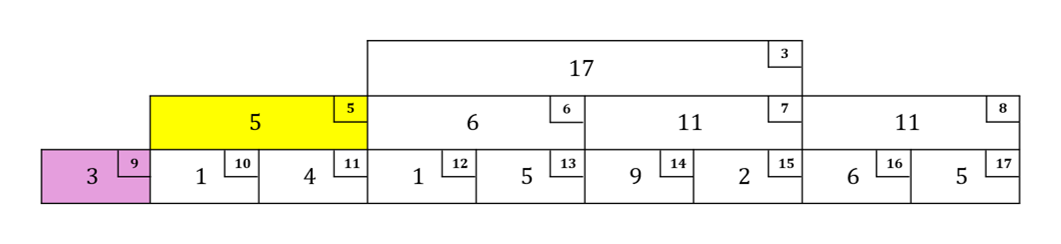
画像13.png
条件を満たすのでのぼり、次の部分も右の子なのでその場で確認：$r = 3, w = 4, l\_val = 8$
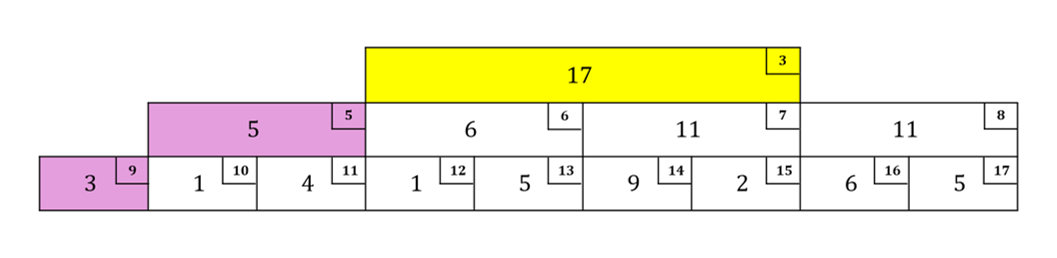
画像14.png
条件を満たさないので１つ目のループ終わり：$r = 3, w = 8, l\_val = 8$（仮に満たしていても$r + w > n$なのでループ終わり）。2つ目のループの1周目は$r = 3, w = 8, l\_val = 8$だが条件を満たさないので2周目へ。さらに、2周目も$r = 3, w = 4, l\_val = 8$で条件を満たさないので3周目から。

左の子を確認：$r = 3, w = 2, l\_val = 8$
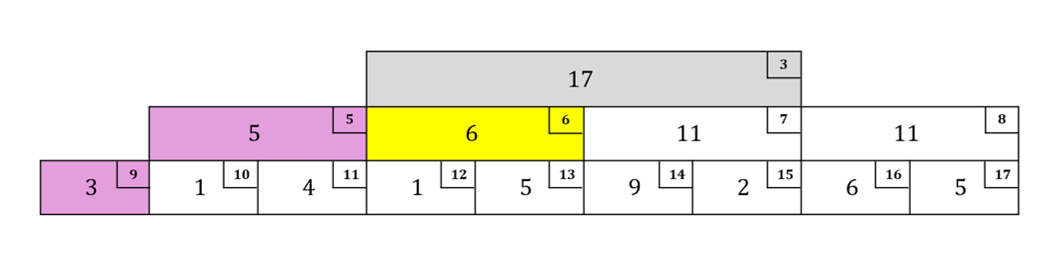
画像15.png
左の子が条件を満たしたので右の子のそのまた（左の）子要素を確認：$r = 5, w = 1, l\_val = 14$
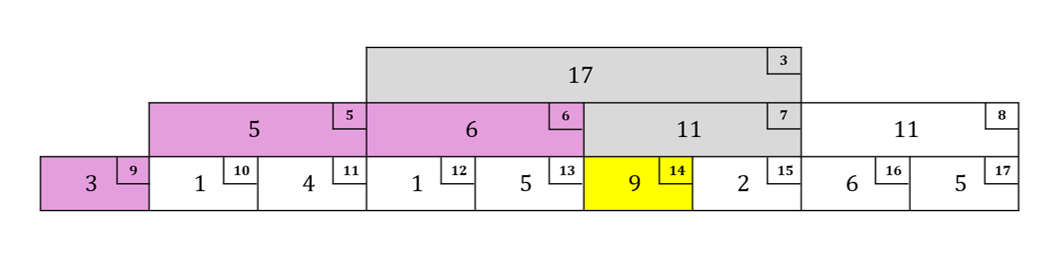
画像16.png
左の子が条件を満たし、$w = 0$となったので2つ目のループ終わり：$r = 6, w = 0, l\_val = 23$
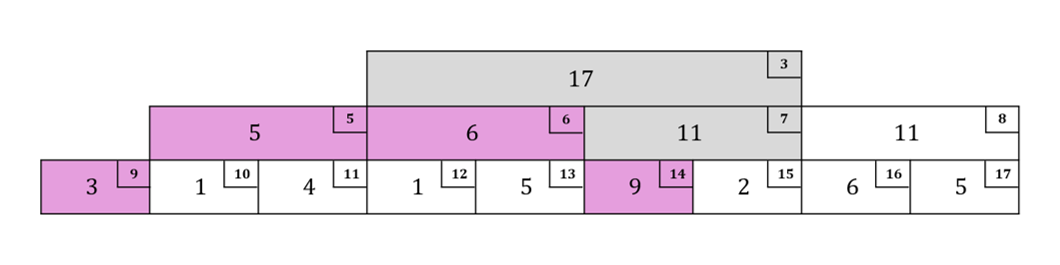
画像17.png

補足

  • 下るとき親の要素は$false$とわかってるので左の子だけ見れば右の子の様子もわかって良いですねー
  • $x$の値によって2つ目のループの$r + w \leq n$がないと上手くいかなかったり...
  • $check$を満たす$query(l, r)$のうち最小の$l$を返す二分探索（min_left）は対称的に実装すればいいです（実装まとめを参照）

実装まとめ

SegmentTree.cpp
template <typename T>
class SegmentTree {
   private:
    using F = function<T(T, T)>;

    int n;
    vector<T> seg;
    const F f;
    const T e;

   public:
    SegmentTree(int n, const F f, const T& e) : n(n), seg(vector<T>(2 * n, e)), f(f), e(e) {}

    SegmentTree(const vector<T>& v, const F f, const T& e) : n(v.size()), seg(2 * n), f(f), e(e) {
        for (int i = 0; i < n; i++) {
            seg[n + i] = v[i];
        }
        for (int i = n - 1; i >= 1; i--) {
            seg[i] = f(seg[i << 1], seg[i << 1 | 1]);
        }
    }

    T operator[](const int i) const { return seg[i + n]; }

    void update(int i, const T& x) {
        i += n;
        seg[i] = x;
        while (i > 1) {
            i >>= 1;
            seg[i] = f(seg[i << 1], seg[i << 1 | 1]);
        }
    }

    T query(int l, int r) {
        l += n;
        r += n;
        T l_val = e;
        T r_val = e;
        while (l < r) {
            if (l & 1) {
                l_val = f(l_val, seg[l]);
                l++;
            }
            if (r & 1) {
                r--;
                r_val = f(seg[r], r_val);
            }
            l >>= 1;
            r >>= 1;
        }
        return f(l_val, r_val);
    }

    template <class S>
    int max_right(int l, S check) const { // max(r) s.t. check(query(l, r)) == true
        assert(0 <= l && l <= n);
        int r = l;
        l += n;
        int w = 1;
        T l_val = e;
        for (; r + w <= n; l >>= 1, w <<= 1) {
            if (l & 1) {
                if (check(f(l_val, seg[l]))) {
                    l_val = f(l_val, seg[l]);
                    r += w;
                    l++;
                } else {
                    break;
                }
            }
        }
        for (; w > 0; l <<= 1, w >>= 1) {
            if (r + w <= n && check(f(l_val, seg[l]))) {
                l_val = f(l_val, seg[l]);
                r += w;
                l++;
            }
        }
        return r;
    }

    template <class S>
    int min_left(int r, S check) const { // min(l) s.t. check(query(l, r)) == true
        assert(0 <= r && r <= n);
        int l = r;
        r += n;
        int w = 1;
        T r_val = e;
        for (; l - w >= 0; r >>= 1, w <<= 1) {
            if (r & 1) {
                if (check(f(seg[r - 1], r_val))) {
                    r_val = f(seg[r - 1], r_val);
                    l -= w;
                    r--;
                } else {
                    break;
                }
            }
        }
        for (; w > 0; r <<= 1, w >>= 1) {
            if (l - w >= 0 && check(f(seg[r - 1], r_val))) {
                r_val = f(seg[r - 1], r_val);
                l -= w;
                r--;
            }
        }
        return l;
    }
};

その他

時間計算量は構築に$O(n)$、その他はセグ木の根の高さが$O(\log n)$なことから$O(\log n)$です（定数倍は重め、1点更新は$O(1)$）。
今回は和を例に挙げましたが、minをのせて二分探索したり、他にのせられるものを考えたりするだけでもちゃんと頭を使う気がします（むずかしい）。

おわりに

よくわからないよーという人は以下の解説を見るといいと思います。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?