完全二分木
完全二分木は根付き木の一つで,各頂点の子は多くても2個であるような木のことです.また,頂点は常に左に詰めて配置されています.ヒープ木も完全二分木の一つで,根の要素が最小値であるような木のことです.根から一番遠い子孫までの路の長さを根の高さと言います.下図の例では根の高さは3となります.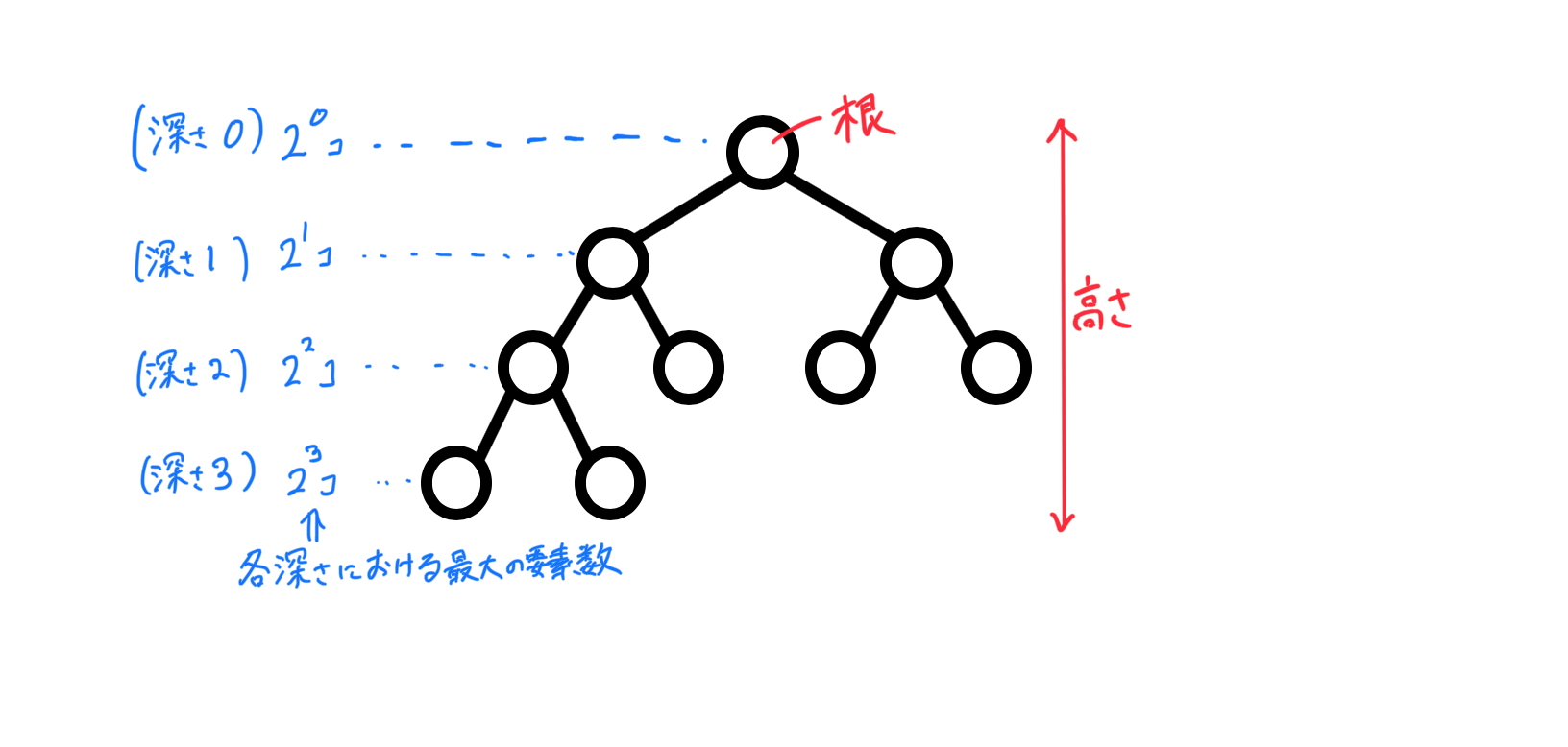
高さのオーダーは?
完全二分木は,根の高さによってその木の要素の最大数は決まっています.例えば,根の高さが3なら最大でも15個です.では,要素の数をnとすると根の高さはどうなるのか?各深さにおける最大の要素数は深さをdとすると,2^d個となります.つまり,根の高さがhの木の場合,最大の要素数は(2^0+2^1+...2^h)個になります.
ここで,
2^0 + 2^1 + ... 2^n = 2^(n+1) - 1
のように最大の要素数を表すことができます.根の高さがhの木の最大の要素数は2^(h+1) - 1個となります.
また,根の高さがh-1の木の最大の要素数は2^(h) - 1個となります
よってn個の要素を含む完全二分木の値の高さは,
2^h - 1 < 2^h <= n < 2^(h+1) - 1 < 2^(h+1)
⇨ 2^h <= n < 2^(h+1)
⇨ h = O(logn)
完全二分木の根の高さはO(logn)であることがわかりました.