はじめに
有限要素法などの解析結果を色付きコンターで表現したい場合がありますが、解析領域の形状は必ずしも矩形とは限らず、工夫が必要となります。そこで、以下の2点について、勉強の記録を残しておくことにします。
1.任意の点で与えられた数値からコンターを作成(meshgrid, interpolate.griddataの活用)
2.作成したコンター領域にマスクをかける(Sympy.geometryの活用)
環境
MacBook Air (M1, 2020, 13.3-inch)
8-core CPU, 7-core GPU
8GB memory, 256GB SSD
macOS Big Sur
Python 3.9.1 (packaged by conda-forge)
(Python及びライブラリはMiniforge3よりインストール)
コンターの作成
x軸範囲0〜8,y軸範囲0〜8の矩形領域を考えます。この領域内において、乱数で与えた (x, y) 座標に対し、高さ z = f(x, y) = y を与え、コンターを描いてみることにします。
ここで、データが与えられている点 (x, y, z) はコンターを書くのに都合よく配置されているわけではないので、以下のように numpy.meshgrig を使ってグリッドを作成した後、scipy.interpolate.griddata により、作成したグリッド上の点に値を与え、コンター作成用データ (xx, yy, zz) を作成します。データ内挿方法としては、scipy.interpolate.griddata に、nearest, linear, cubic の3種類が準備されています。nearest は結果が他と違うイメージとなりますが、 linear, cubic は概ね同一の結果が得られます。グリッド作成と内挿部分のコードを下に示します。
# making meshgrid and interpolation
ds=0.2 # interval of grid
x1 = np.arange(xmin, xmax+ds, ds)
y1 = np.arange(ymin, ymax+ds, ds)
xx, yy = np.meshgrid(x1, y1)
zz = interpolate.griddata((x,y), z, (xx, yy), method='nearest')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='linear')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='cubic')
上記により、グリッド上のデータ (xx, yy, zz) が出来上がれば、以下により色塗りコンターを描画できます。この例では cmap='jet' としています。
plt.contourf(xx,yy,zz,cmap='jet')
作図事例
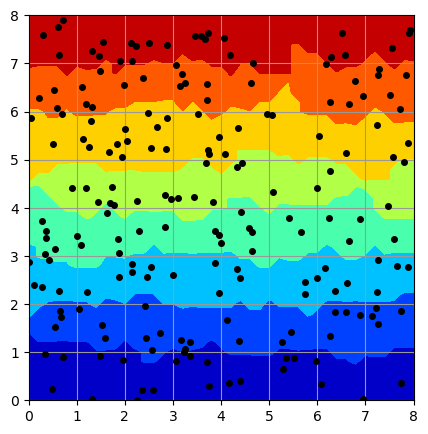
method='nearest' では、meshgrid で指定した全領域が色付けされています。色付け結果は傾向はつかめていますが、きれいな線形分布にはなっていません。
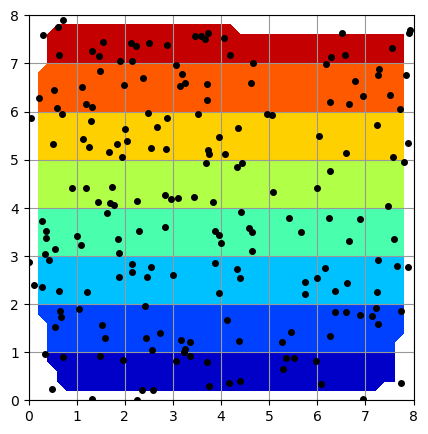
method='cubic' では、meshgrid で指定した全領域が色付けされているわけではなく、黒点で示した原データ点の内側に色付けがなされています。色付け結果はきれいな線形分布になっています。
事例1(method='nearest')
事例2(method='cubic')
プログラム
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
import time
def drawfig(xx,yy,zz,x,y):
# drawing
plt.figure(figsize=(5,5),facecolor='w')
plt.grid(color='#999999',linestyle='solid')
plt.gca().set_aspect('equal',adjustable='box')
plt.contourf(xx,yy,zz,cmap='jet')
plt.plot(x,y,'o',ms=4,color='#000000')
fnameF='fig_test2.png'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
def main():
start=time.time()
# data of points
xmin, xmax=0, 8
ymin, ymax=0, 8
n=200
np.random.seed(seed=31)
x=xmin+(xmax-xmin)*np.random.rand(n)
y=ymin+(ymax-ymin)*np.random.rand(n)
z=y
# making meshgrid and interpolation
ds=0.2
x1 = np.arange(xmin, xmax+ds, ds)
y1 = np.arange(ymin, ymax+ds, ds)
xx, yy = np.meshgrid(x1, y1)
zz = interpolate.griddata((x,y), z, (xx, yy), method='nearest')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='linear')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='cubic')
# drawing
drawfig(xx,yy,zz,x,y)
print(time.time()-start)
# ---------------
# Execute
# ---------------
if __name__ == '__main__': main()
マスク作成の準備(内外判定)
コンター図にマスクをかけるための準備を行います。ここでは機械的に処理するため、多角形で規定された領域の内外判定を、sympy.geometryを用いて行います。この部分は、以下の投稿を参照させていただきました。
SymPy Geometry 学習メモ(多角形)
https://qiita.com/code0327/items/1a4d8c587ccdf7a0bc62
課題は、指定した x-y 平面上の点が、同じく x-y 平面上で指定された多角形領域に含まれるか否かを判定するものです。多角形領域は、上記投稿のものを使わせていただきました。図形の意味は別として、多角形内に水平線・傾斜線・鉛直線が含まてており、例題用の多角形として面白いので、そのまま使わせていただくことにしました。sympy.geometry の Point と Polygon を用います。
Geometry
https://docs.sympy.org/latest/modules/geometry/index.html
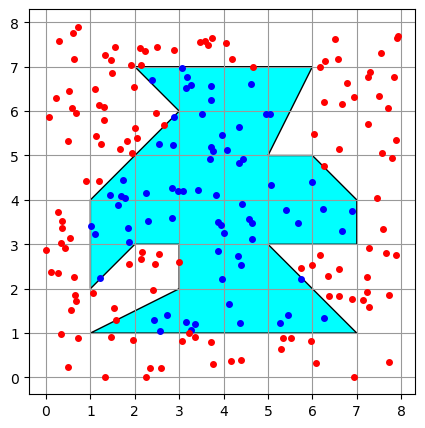
作図例
乱数で与えた 200 個の点が、指定した多角形領域の内側か外側かを判定しています。赤点が外側、青点が内側判定です。
プログラム
Geometry の使用例では、座標をタプルで渡していますが、numpy 配列を渡しても ok でした。
内外判定は以下の文で行っています。x, y は判定したい点の座標、poly には領域を規定する多角形の座標が格納されています。
s=poly.encloses_point(Point(x,y))
指定点が領域に含まれれば、s=True、含まれなければ s=False となります。ここで、「指定した多角形の境界線上は外側判定(False)」 となることに注意が必要です。
また、polyは以下のように定義します。
xb=[1,3,3,2,1,1,3,2,6,5,6,7,7,5,7]
yb=[1,2,3,3,2,4,6,7,7,5,5,4,3,3,1]
bxy = np.zeros((len(xb),2), dtype=np.float64)
for i in range(len(xb)):
bxy[i,0]=xb[i]
bxy[i,1]=yb[i]
poly=Polygon(*bxy)
xb, yb は多角形を指定する x 座標および y 座標のリスト( numpy 配列でも可)。これより2次元配列 bxy を作成し、polyに読み込みます。この時、poly=Polygon(*bxy) とアスタリスクを付ける必要があります。アスタリスクがないと以下のエラーがでます。
ValueError: Nonzero coordinates cannot be removed.
プログラム全文を以下に示します。
from sympy.geometry import Point, Polygon
import matplotlib.pyplot as plt
import numpy as np
import time
def drawfig(xb,yb,xp,yp,ss):
# drawing
plt.figure(figsize=(5,5),facecolor='w')
plt.grid(color='#999999',linestyle='solid')
plt.gca().set_aspect('equal',adjustable='box')
plt.fill(xb,yb,color='#00ffff',edgecolor='#000000')
for i in range(len(xp)):
if ss[i]==True : col='#0000ff'
if ss[i]==False: col='#ff0000'
plt.plot(xp[i],yp[i],'o',ms=4,color=col)
fnameF='fig_test1.png'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
def main():
start=time.time()
# boundary
xb=[1,3,3,2,1,1,3,2,6,5,6,7,7,5,7]
yb=[1,2,3,3,2,4,6,7,7,5,5,4,3,3,1]
bxy = np.zeros((len(xb),2), dtype=np.float64)
for i in range(len(xb)):
bxy[i,0]=xb[i]
bxy[i,1]=yb[i]
poly=Polygon(*bxy)
# points for judgement
xmin, xmax=0, 8
ymin, ymax=0, 8
n=200
np.random.seed(seed=31)
xp=xmin+(xmax-xmin)*np.random.rand(n)
yp=ymin+(ymax-ymin)*np.random.rand(n)
# judgement (True or False)
# In case of point beeing just on the boundary, result is 'False'
ss=[]
for x,y in zip(xp,yp):
s=poly.encloses_point(Point(x,y))
ss=ss+[s]
# drawing
drawfig(xb,yb,xp,yp,ss)
print(time.time()-start)
# ---------------
# Execute
# ---------------
if __name__ == '__main__': main()
コンター図にマスクをかける(1)
コンター図にマスクをかけてみます。マスク形状は、上記で指定した多角形とします。コンター図は、meshgrid で生成した座標に対して描かれているので、コンター図にマスクをかけるには、meshgrid で生成した点の、指定多角形に対する内外判定を行う必要があります。指定領域の外側の点に対しては zz[jj,ii]=np.nan を指定してコンターの未定義領域とします。
matplotlib, Contourf Demo
https://matplotlib.org/stable/gallery/images_contours_and_fields/contourf_demo.html
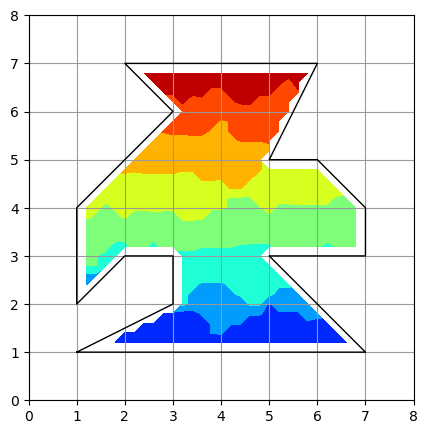
作図例
マスクがかかって、指定多角形領域の外にはコンターによる色付けはなされていません。しかしながら、描かれているコンターは指定多角形(黒実線)の内側になっており、これを成果とするには今ひとつです。ここでは、meshgrid のメッシュ間隔は 0.2 としており、境界上の点は外側判定されるため、コンターが描かれる範囲がその分内側になっていると考えられます。
プログラム
from sympy.geometry import Point, Polygon
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
import time
def drawfig(xx,yy,zz,xb,yb):
# drawing
plt.figure(figsize=(5,5),facecolor='w')
plt.grid(color='#999999',linestyle='solid')
plt.gca().set_aspect('equal',adjustable='box')
plt.plot(np.append(xb,xb[0]),np.append(yb,yb[0]),'-',color='#000000',lw=1)
plt.contourf(xx,yy,zz,cmap='jet')
fnameF='fig_test3.png'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
def main():
start=time.time()
# boundary
xb=np.array([1,3,3,2,1,1,3,2,6,5,6,7,7,5,7])
yb=np.array([1,2,3,3,2,4,6,7,7,5,5,4,3,3,1])
bxy = np.zeros((len(xb),2), dtype=np.float64)
for i in range(len(xb)):
bxy[i,0]=xb[i]
bxy[i,1]=yb[i]
poly=Polygon(*bxy)
# data of points
xmin, xmax=0, 8
ymin, ymax=0, 8
n=200
np.random.seed(seed=31)
x=xmin+(xmax-xmin)*np.random.rand(n)
y=ymin+(ymax-ymin)*np.random.rand(n)
z=y
# makeing mrshgrid and interpolation
ds=0.2
x1 = np.arange(xmin, xmax+ds, ds)
y1 = np.arange(ymin, ymax+ds, ds)
xx, yy = np.meshgrid(x1, y1)
zz = interpolate.griddata((x,y), z, (xx, yy), method='nearest')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='linear')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='cubic')
# judgement (True or False)
# In case of point beeing just on the boundary, result is 'False'
xp=xx[0,:]
yp=yy[:,0]
ii=[]
jj=[]
for i in range(len(xp)):
for j in range(len(yp)):
s=poly.encloses_point(Point(xp[i],yp[j]))
if s==False:
ii=ii+[i]
jj=jj+[j]
zz[jj,ii]=np.nan
# drawing
drawfig(xx,yy,zz,xb,yb)
print(time.time()-start)
# ---------------
# Execute
# ---------------
if __name__ == '__main__': main()
コンター図にマスクをかける(2)
上述の結果では満足できませんが、対策としてはどうすればよいのでしょうか?
ひとつは meshgrid の間隔を小さくすることです。この場合コンターデータ作成にかかる時間は大して気になりませんが、領域の内外判定にとても時間がかかってしまい、耐えられません。
もうひとつの方法は、内外判定する指定多角形領域を拡大し、結果的に描画される領域を指定領域と概ね等しくする方法であり、こちらにトライしました。
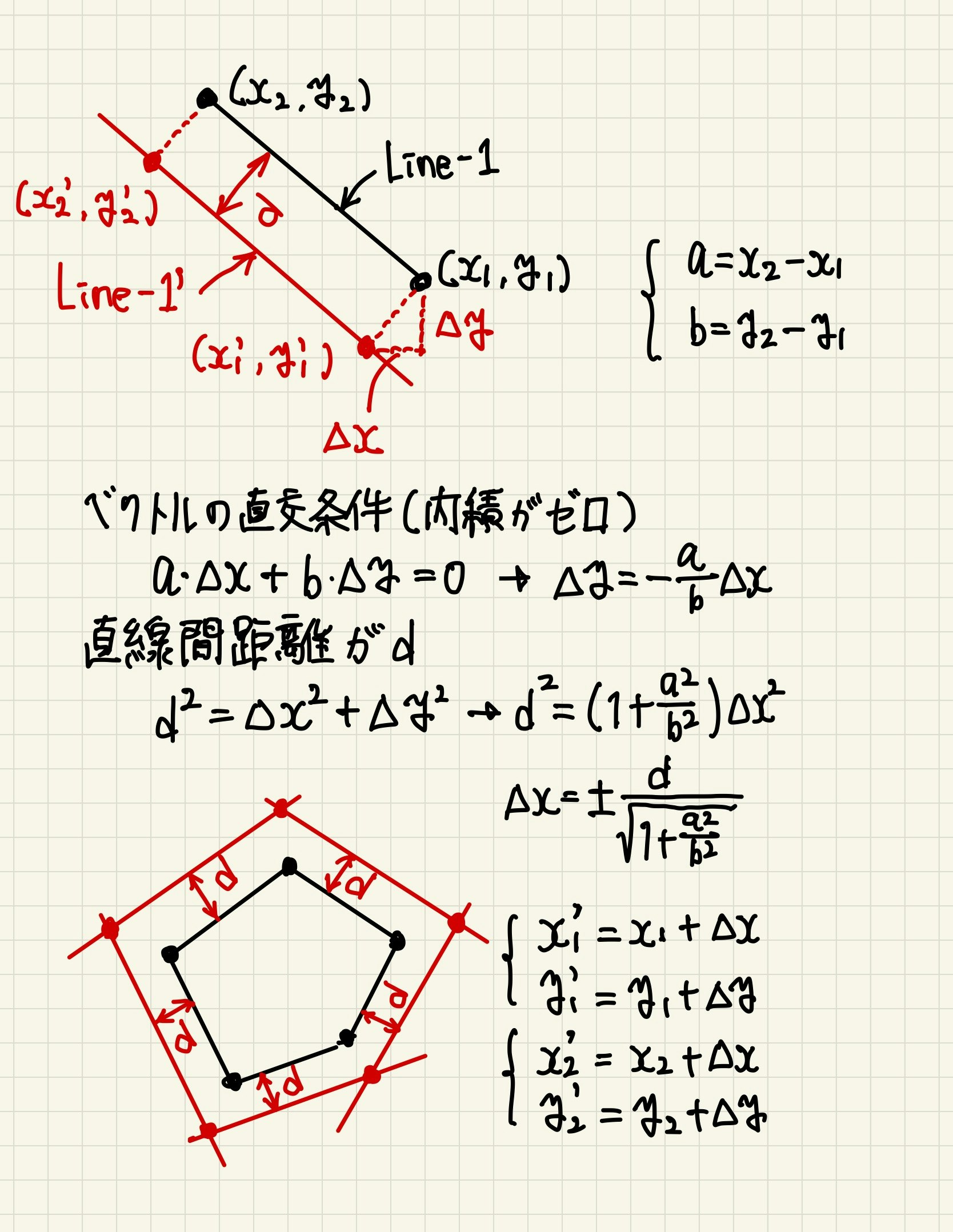
考え方は、指定領域を構成する線分に対し、一定距離を持つ平行線を考え、その平行線の交点に指定領域を示す点を移動させ、これを内外判定のための指定領域とするものです。考え方の概要を以下に示します。なお、多角形の頂点は時計回りに入力することを前提としています。(余談ですが、下記図は iPad の GoodNotes 5 で作成したもの。プログラム作成時に描くこのような手書き図を作成・保存できるのが iPad のいいところです。キタナイジデゴメンナサイ)
作図例
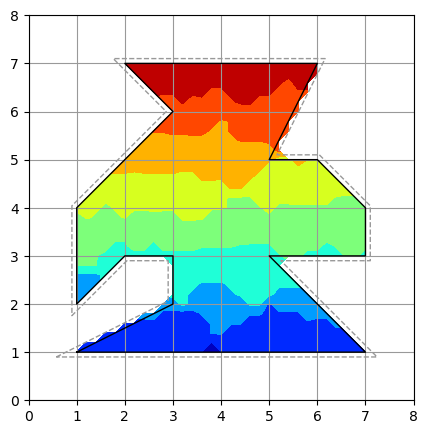
作図例は、本来の領域(黒実線)に対し、マスクをかけるための内外判定の領域を、meshgrig の間隔 0.2 の半分の 0.1 とした場合(本来の領域の外側に破線で表示)についてのものです。meshgrid の間隔が 0.2 のため、傾斜線部はギザギザしていますが、概ね必要領域をカバーできています。
プログラム
from sympy.geometry import Point, Polygon
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
import time
def line1(p1,q1,p2,q2,ds):
# conversion of point coordinates
a=p2-p1
b=q2-q1
if 0<b:
dx=-ds/np.sqrt(1+a**2/b**2)
dy=-a/b*dx
if b<0:
dx= ds/np.sqrt(1+a**2/b**2)
dy=-a/b*dx
if b==0 and 0<a:
dx=0
dy=ds
if b==0 and a<0:
dx=0
dy=-ds
xx1=p1+dx
yy1=q1+dy
xx2=p2+dx
yy2=q2+dy
return xx1,yy1,xx2,yy2
def refb(xb,yb,ds):
# reference boundary
xc=np.zeros(len(xb),dtype=np.float64)
yc=np.zeros(len(yb),dtype=np.float64)
for i in range(len(xb)):
if i==0:
x1=xb[-1] ; y1=yb[-1]
x2=xb[i] ; y2=yb[i]
x3=xb[i+1]; y3=yb[i+1]
if 1<=i<len(xb)-1:
x1=xb[i-1]; y1=yb[i-1]
x2=xb[i] ; y2=yb[i]
x3=xb[i+1]; y3=yb[i+1]
if i==len(xb)-1:
x1=xb[i-1]; y1=yb[i-1]
x2=xb[i] ; y2=yb[i]
x3=xb[0] ; y3=yb[0]
xx1a,yy1a,xx2a,yy2a=line1(x1,y1,x2,y2,ds)
xx1b,yy1b,xx2b,yy2b=line1(x2,y2,x3,y3,ds)
if xx2a-xx1a==0 and xx2b-xx1b!=0:
aa2=(yy2b-yy1b)/(xx2b-xx1b)
bb2=(xx2b*yy1b-xx1b*yy2b)/(xx2b-xx1b)
xc[i]=xx2a
yc[i]=aa2*xc[i]+bb2
if xx2a-xx1a!=0 and xx2b-xx1b==0:
aa1=(yy2a-yy1a)/(xx2a-xx1a)
bb1=(xx2a*yy1a-xx1a*yy2a)/(xx2a-xx1a)
xc[i]=xx2b
yc[i]=aa1*xc[i]+bb1
if xx2a-xx1a!=0 and xx2b-xx1b!=0:
aa1=(yy2a-yy1a)/(xx2a-xx1a)
bb1=(xx2a*yy1a-xx1a*yy2a)/(xx2a-xx1a)
aa2=(yy2b-yy1b)/(xx2b-xx1b)
bb2=(xx2b*yy1b-xx1b*yy2b)/(xx2b-xx1b)
xc[i]=(bb2-bb1)/(aa1-aa2)
yc[i]=(aa1*bb2-bb1*aa2)/(aa1-aa2)
return xc,yc
def drawfig(xx,yy,zz,xb,yb,xc,yc):
# drawing
plt.figure(figsize=(5,5),facecolor='w')
plt.grid(color='#999999',linestyle='solid')
plt.gca().set_aspect('equal',adjustable='box')
plt.plot(np.append(xb,xb[0]),np.append(yb,yb[0]),'-',color='#000000',lw=1)
plt.plot(np.append(xc,xc[0]),np.append(yc,yc[0]),'--',color='#999999',lw=1)
plt.contourf(xx,yy,zz,cmap='jet')
fnameF='fig_test4.png'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
def main():
start=time.time()
ds=0.2 # interval of grid for interpolation
# boundary
xb=np.array([1,3,3,2,1,1,3,2,6,5,6,7,7,5,7])
yb=np.array([1,2,3,3,2,4,6,7,7,5,5,4,3,3,1])
xc,yc=refb(xb,yb,ds*0.5)
bxy = np.zeros((len(xc),2), dtype=np.float64)
for i in range(len(xc)):
bxy[i,0]=xc[i]
bxy[i,1]=yc[i]
poly=Polygon(*bxy)
# data of points
xmin, xmax=0, 8
ymin, ymax=0, 8
n=200
np.random.seed(seed=31)
x=xmin+(xmax-xmin)*np.random.rand(n)
y=ymin+(ymax-ymin)*np.random.rand(n)
z=y
# making meshgrid and interpolation
x1 = np.arange(xmin, xmax+ds, ds)
y1 = np.arange(ymin, ymax+ds, ds)
xx, yy = np.meshgrid(x1, y1)
zz = interpolate.griddata((x,y), z, (xx, yy), method='nearest')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='linear')
#zz = interpolate.griddata((x,y), z, (xx, yy), method='cubic')
# judgement (True or False)
# In case of point beeing just on the boundary, result is 'False'
xp=xx[0,:]
yp=yy[:,0]
ii=[]
jj=[]
for i in range(len(xp)):
for j in range(len(yp)):
s=poly.encloses_point(Point(xp[i],yp[j]))
if s==False:
ii=ii+[i]
jj=jj+[j]
zz[jj,ii]=np.nan
# drawing
drawfig(xx,yy,zz,xb,yb,xc,yc)
print(time.time()-start)
# ---------------
# Execute
# ---------------
if __name__ == '__main__': main()
おわりに
M1 MacBook Air による計算時間を示します。
| 処理 | 所要時間 |
|---|---|
| コンター図作成 | 0.15 sec |
| 内外判定 | 12.19 sec |
| コンター図作成+マスク(1) | 19.75 sec |
| コンター図作成+マスク(2) | 22.84 sec |
表からわかるように、コンター図作成は結構早いのですが、内外判定に多くの時間が取られています。
内外判定は、汎用性を求めて、meshgrid の全領域を走査していることも、時間がかかる原因となっています。ここらは時間短縮できればありがたい限りです。
以 上