はじめに
sympy.geometry の学習メモ ~多角形~ です。「SymPy Geometory 学習メモ(点・直線)」のつづきです。複雑な形状(凸形・凹型)の多角形の面積や外周長さを求めることをゴールにします。
Pythonのバージョンは 3.6.8、SymPiのバージョンは 1.3 を使用しました。
import sys
import sympy
print(f'Python {sys.version}')
print(f'SymPi {sympy.__version__}')
多角形
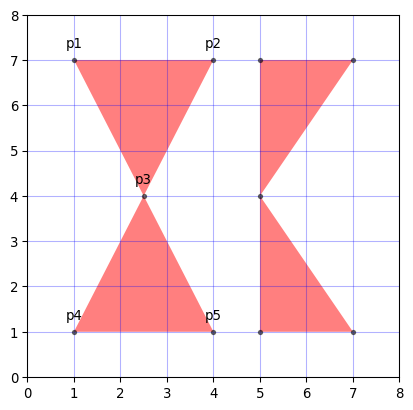
**多角形(ポリゴン)**は、点のリスト/タプルを与えて生成することができます。次のプログラムでは、凸多角形、凹多角形(非凸多角形)、自己交差する多角形のポリゴンを生成しています。また、この後の理解を助けるために、matplotlibでXY座標上に図示しています。
なお、SymPy 1.1.1 では「GeometryError: Polygon has intersecting sides.」というエラーにより、自己交差する多角形は生成不能でした。
from sympy.geometry import *
import matplotlib.pyplot as plt
%matplotlib inline
# ポリゴン(多角形)の生成
tmp = ((1,1),(4,3),(5,1))
p0 = Polygon( *tmp ) # 凸多角形
tmp = ((1,4),(4,6),(5,4),(5,7),(1,7))
p1 = Polygon( *tmp ) # 凹多角形
tmp = ((5.5,2.0),(7.5,6.0),(6.0,6.0),(7.0,2.0))
p2 = Polygon( *tmp ) # 自己交差多角形
polygons = [p0,p1,p2]
# グラフ描画
plt.figure(figsize=(5,5),dpi=96)
for p in polygons :
tmp = list(map(lambda p:(float(p.x),float(p.y)), p.vertices))
tmp = plt.Polygon(tmp,fc='red',alpha=0.5)
plt.gca().add_patch(tmp)
xRange=yRange=(0,8)
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0],xRange[1]+1))
plt.yticks(range(yRange[0],yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
面積は .area で、外周は perimeterで、凸多角形かどうかは .is_convex() で簡単に知ることができます。
for i,p in enumerate(polygons) :
print( f'p{i} :',end=' ')
print( f'面積 {float(p.area):5.1f}' ,end=' ')
print( f'外周 {float(p.perimeter):5.1f}',end=' ')
print( f'凸形か {p.is_convex()}')
p0 : 面積 -4.0 外周 9.8 凸形か True
p1 : 面積 8.0 外周 15.8 凸形か False
p2 : 面積 0.0 外周 11.6 凸形か False
面積については、注意が必要です。上記の結果をみると p0 の面積が「-4.0」と負の値になっています。多角形を生成する際に、時計回り(CW) に点を与えると面積が負になります。一方、反時計周り(CCW) に与えると面積は正になります。
tmp = [(1,1),(4,3),(5,1)]
print(Polygon( *tmp ).area) # -4
tmp.reverse()
print(Polygon( *tmp ).area) # 4
つづいて、p3 の面積が 0.0 になっている理由ですが、これは自己交差により「時計周り領域」と「反時計周り領域」が形成され、面積が正負で相殺された結果です。今回は、上半分の逆三角形と、下半分の三角形の面積がたまたま一致したため 0.0 になっています。残念ながら自己交差を含んでいると面積を適切に求めることができません。
自己交差があるかを判定したい
凸多角形であるかは .is_convex() で判定できるのですが、凹多角形のときに「自己交差を含むかどうか?」を判定するものは用意されていないようです(なお、凸多角形では自己交差はあり得ない)。ここでは、自己交差のある凹多角形を 不正なポリゴン と呼ぶことにして、それを判定する方法を考えます。
たぶん効率の良い方法があるとは思うのですが、ここでは力業、つまり、多角形を構成する辺(線分)の全組合せについて「交差があるか」を総当たりで調べていきます。また、次のように「1点で3辺以上が接触している場合」も、ここでは不正なポリゴンに含めます(左側のポリゴンでも「$p1\to p3\to $ $p4\to p5$ $\to p3\to p2$」の順で点をつなげば自己交差はしていませんが、これと「$p1\to p3\to $ $p5\to p4$ $\to p3\to p2$」を区別することが難しいため)。
まず、多角形を構成数する辺は p.sides により、Segment のリストとして取得できます。次に、このリストから2辺を組合せを取り出しますが、これには itertools.combinations を利用します。そして、前回に取り上げた .intersection() を使って交差があるかを調べます。
ただし、次のように、多角形を構成している隣り合う2辺についてチェックした場合、その接点も交差と判定されてしまうので、それは無視する必要があります。
# 交差しない場合
s1 = Segment((0,0),(0,2))
s2 = Segment((2,0),(2,2))
print(s1.intersection(s2)) # []
# 隣り合う2辺の場合 → 端点の接触により交差が検出される
s1 = Segment((0,0),(2,2))
s2 = Segment((2,2),(2,4))
print(s1.intersection(s2)) # [Point2D(2, 2)]
# 辺の端点が、他方の線上(端点以外)に接する場合 →【不正なポリゴン】
s1 = Segment((0,2),(2,0))
s2 = Segment((0,0),(0,4))
print(s1.intersection(s2)) # [Point2D(0, 2)]
# 交差する場合 →【不正なポリゴン】
s1 = Segment((1,0),(1,2))
s2 = Segment((0,1),(2,1))
print(s1.intersection(s2)) # [Point2D(1, 1)]
# 辺が重なっている場合 →【不正なポリゴン】
s1 = Segment((0,0),(0,2))
s2 = Segment((0,0),(0,3))
print(s1.intersection(s2)) # [Segment2D(Point2D(0, 0), Point2D(0, 2))]
これらを踏まえて、次のようにしました。
from sympy.geometry import *
import matplotlib.pyplot as plt
import itertools
%matplotlib inline
# ポリゴン(多角形)の生成
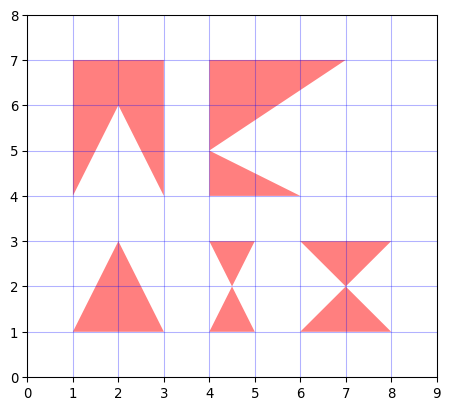
p0 = Polygon( (1,1),(2,3),(3,1) )
p1 = Polygon( (1,4),(2,6),(3,4),(3,7),(1,7) )
p2 = Polygon( (4,1),(5,3),(4,3),(5,1) )
p3 = Polygon( (6,3),(7,2),(6,1),(8,1),(7,2),(8,3) )
p4 = Polygon( (4,7),(4,4),(6,4),(4,5),(7,7) )
polygons = [p0,p1,p2,p3,p4]
# グラフ描画
plt.figure(figsize=(5.5,5),dpi=96)
for p in polygons :
tmp = list(map(lambda p:(float(p.x),float(p.y)), p.vertices))
tmp = plt.Polygon(tmp,fc='red',alpha=0.5)
plt.gca().add_patch(tmp)
xRange=(0,9)
yRange=(0,8)
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0],xRange[1]+1))
plt.yticks(range(yRange[0],yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
def is_valid(p) :
if p.is_convex() : # 凸多角形の場合
return True
if len(p.vertices) != len(set(p.vertices)) :
return False
for (s1,s2) in itertools.combinations(p.sides,2):
cp = s1.intersection(s2)
if len(cp) == 0 :
continue
if cp[0] in s1.points and cp[0] in s2.points :
continue
else :
return False
return True
for i,p in enumerate(polygons) :
print( f'p{i} :',end=' ')
print( f'面積 {float(p.area):5.1f}' ,end=' ')
print( f'外周 {float(p.perimeter):5.1f}',end=' ')
print( f'凸形? {p.is_convex()}',end=' ')
print( f'不正? {not is_valid(p)}')
実行結果は、次のようになります。
p0 : 面積 -2.0 外周 6.5 凸形? True 不正? False
p1 : 面積 4.0 外周 12.5 凸形? False 不正? False
p2 : 面積 0.0 外周 6.5 凸形? False 不正? True
p3 : 面積 2.0 外周 9.7 凸形? False 不正? True
p4 : 面積 4.0 外周 13.8 凸形? False 不正? True
$p2$ は明らかな自己交差により不正なポリゴン認定、$p3$ と $p4$ は自己交差はありませんが1点で3辺以上が接触しているので不正が認定されています。
点が多角形の内部にあるか調べたい
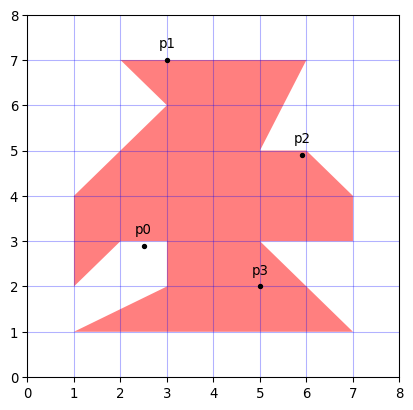
ある点が多角形の内部にあるかどうかは .encloses_point でチェック可能です。境界線上は False と判断されます。
from sympy.geometry import *
import matplotlib.pyplot as plt
%matplotlib inline
# ポリゴン(多角形)の生成
poly = Polygon( *((1,1),(3,2),(3,3),(2,3),(1,2),(1,4),
(3,6),(2,7),(6,7),(5,5),(6,5),(7,4),
(7,3),(5,3),(7,1)) )
# ポイント(点)の生成
p0 = Point(2.5, 2.9)
p1 = Point(3.0, 7.0) # 境界線上
p2 = Point(5.9, 4.9)
p3 = Point(5, 2)
points = [p0, p1, p2, p3]
# グラフ描画
plt.figure(figsize=(5,5),dpi=96)
tmp = list(map(lambda p:(float(p.x),float(p.y)), poly.vertices))
tmp = plt.Polygon(tmp,fc='red',alpha=0.5)
plt.gca().add_patch(tmp)
for i,p in enumerate(points) :
plt.plot(p.x, p.y, color='0.0',marker='.')
plt.text(p.x, p.y + 0.2, 'p{0}'.format(i) , size=10,
horizontalalignment='center', verticalalignment='bottom')
xRange=yRange=(0,8)
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0],xRange[1]+1))
plt.yticks(range(yRange[0],yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
for i,p in enumerate(points) :
print( f'p{i} : 多角形の内部に存在するか? {poly.encloses_point(p)}' )
p0 : 多角形の内部に存在するか? False
p1 : 多角形の内部に存在するか? False
p2 : 多角形の内部に存在するか? True
p3 : 多角形の内部に存在するか? True