はじめに
sympy.geometry の学習メモ ~点・直線 編~ です。
sympy.geometry(SymPiのGeometryモジュール)では、主に2次元平面上の点、直線、多角形、円などについて外周長さや面積の計算、交差判定などができます。3次元空間における直線や平面も扱うことができますが、ここでは対象外とします。
Pythonのバージョンは 3.6.8、SymPiのバージョンは 1.3 を使用しました。
import sys
import sympy
print(f'Python {sys.version}')
print(f'SymPi {sympy.__version__}')
点
点を定義して、2点間の距離や中点、3つ以上の点が同一直線上にあるか?などを調べることができます。
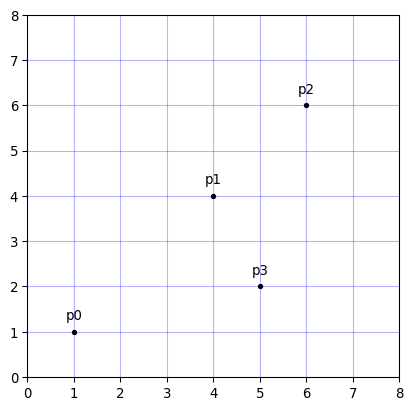
次のコードは $p0$ から $p4$ までの 4点 を生成するものです。また、後ほど求める距離や中点などを視覚的に確認するために matplotlib でグラフ上に点をプロットしておきます。
from sympy.geometry import *
import matplotlib.pyplot as plt
%matplotlib inline
# ポイント(点)の生成
p0 = Point(1, 1)
p1 = Point(4, 4)
p2 = Point(6, 6)
p3 = Point(5, 2)
# グラフ描画
points = [p0, p1, p2, p3]
plt.figure(figsize=(5,5),dpi=96)
for i,p in enumerate(points) :
plt.plot(p.x, p.y, color='0.0',marker='.')
plt.text(p.x, p.y + 0.2, 'p{0}'.format(i) , size=10,
horizontalalignment='center', verticalalignment='bottom')
xRange=yRange=(0,8)
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0],xRange[1]+1))
plt.yticks(range(yRange[0],yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
これらの点について、sympy.geometory を利用して距離や中点などを求めていきます。
print(f'(1) type = {type(p1)}') # 型
print(f'(2) (x,y)=({p1.x},{p1.y})') # 座標の参照
print(f'(3) p0とp3の距離 = {p0.distance(p3)}') # 2点間の距離
print(f'(4) p0とp3の中点 = {p0.midpoint(p3)}') # 中点
print(f'(5-1) {Point.is_collinear(p0,p1,p2)}') # 同一直線上にあるか?
print(f'(5-2) {Point.is_collinear(p1,p2,p3)}') # 同一直線上にあるか?
print(f'(5-3) {Point.is_collinear(p0,p1,p2,p3)}') # 同一直線上にあるか?
(1) type = <class 'sympy.geometry.point.Point2D'>
(2) (x,y)=(4,4)
(3) p0とp3の距離 = sqrt(17)
(4) p0とp3の中点 = Point2D(3, 3/2)
(5-1) True
(5-2) False
(5-3) False
計算に平方根を含む場合は、そのまま出力されます。float型に変換するためには float(p0.distance(p3)) のように float() を利用します。
線(線分・直線)
直線(Line) と 線分(Segment) が区別されます。Line は2次元平面上を無限にどこまでも伸びていきます。一方、Segment は端点が与えられています。
線分
端点が与えられ、長さが有限の Segment(線分)は、先ほどの点(Point)を2個与えて生成します。
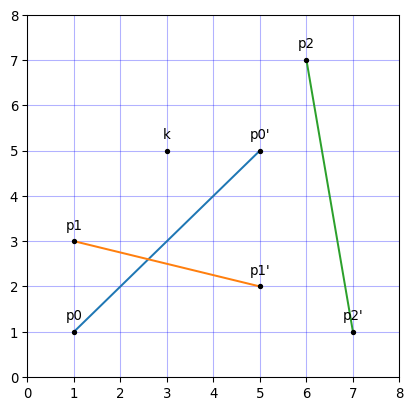
次のプログラムでは、3つの線分と1つの点を生成しています。
from sympy.geometry import *
import matplotlib.pyplot as plt
%matplotlib inline
# ポイント(点)の生成
k = Point(3, 5)
# セグメント(線分)の生成
s0 = Segment(Point(1, 1),Point(5,5))
s1 = Segment((1, 3),(5,2)) # Point()は省略可能
s2 = Segment((6, 7),(7,1)) # Point()は省略可能
segments = [s0,s1,s2]
# グラフ描画
plt.figure(figsize=(5,5),dpi=96)
for i,s in enumerate(segments) :
plt.plot([s.p1.x, s.p2.x], [s.p1.y, s.p2.y])
pn = 'p' + str(i)
for p, m in zip( s.points,('',"'") ) :
plt.plot(p.x, p.y, color='0.0',marker='.')
plt.text(p.x, p.y + 0.2, pn+m , size=10,
horizontalalignment='center', verticalalignment='bottom')
plt.plot(k.x, k.y, color='0.0',marker='.')
plt.text(k.x, k.y + 0.2, 'k', size=10,
horizontalalignment='center', verticalalignment='bottom')
xRange=yRange=(0,8)
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0],xRange[1]+1))
plt.yticks(range(yRange[0],yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
Segment(線分)については、長さ、中点、2つの線分の交点などを求めることができます。傾きをダイレクトに取得できる関数・プロパティが見当たらなかったので gradient という関数を自作しています(Line(直線)の場合は slope というプロパティで取得可能なのですが・・・)。
print(f'(1) type = {type(s0)}') # 型
print(f'(2) length = {s0.length}') # 長さ
print(f'(3) direction = {s0.direction}') # 方向?
gradient = lambda s: s.direction.y / s.direction.x
print(f'(4-1) 線分s0の傾き = {gradient(s0)}') # 傾き
print(f'(4-2) 線分s1の傾き = {gradient(s1)}') # 傾き
print(f'(4-3) 線分s2の傾き = {gradient(s2)}') # 傾き
print(f'(5) 中点 = {s0.midpoint}')
print(f'(6) 点kとの距離 = {s0.distance(k)}')
print(f'(7-1) 線分s0と線分s1の交点 = {s0.intersection(s1)}')
print(f'(7-2) 線分s0と線分s2の交点 = {s0.intersection(s2)}')
(1) type = <class 'sympy.geometry.line.Segment2D'>
(2) length = 4*sqrt(2)
(3) direction = Point2D(4, 4)
(4-1) 線分s0の傾き = 1
(4-2) 線分s1の傾き = -1/4
(4-3) 線分s2の傾き = -6
(5) 中点 = Point2D(3, 3)
(6) 点kとの距離 = sqrt(2)
(7-1) 線分s0と線分s1の交点 = [Point2D(13/5, 13/5)]
(7-2) 線分s0と線分s2の交点 = []
線分同士の交点を求めると結果はリストで返されます。線分$s0$ と $s1$ の交点は $(2.6, 2.6)$ 、線分$s0$ と $s2$ の交点は「無し(空のリスト)」で、この結果が正しいことはグラフから視覚的に確認できます($13/5=2.6$)。
また、distance により、任意の点との距離を求めることもできます。
直線
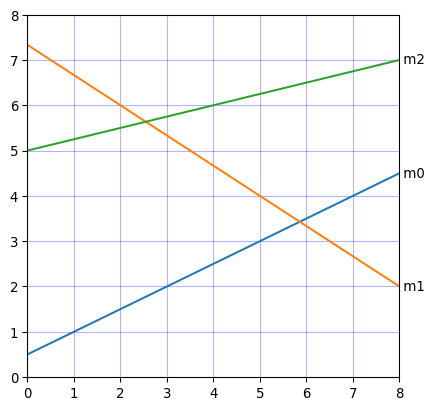
今度は、空間を無限に伸びていく Line(直線)を扱います。直線は「2点を与える」「1点とと傾きを与える」「Segment(線分)を与える」によって生成することができます。
import sympy
from sympy.geometry import *
import matplotlib.pyplot as plt
%matplotlib inline
# ライン(直線)の生成
m0 = Line( Point(1, 1), Point(3,2) )
m1 = Line( (2,6), slope = sympy.Rational(-2,3) ) # 傾き -2/3
m2 = Line( Segment((0, 5),(4,6)) ) # 線分から生成
lines = [m0,m1,m2]
# グラフ描画
plt.figure(figsize=(5,5),dpi=96)
xRange=yRange=(0,8)
# 描画のために x=0 と x=8 の直線(グラフ両端の垂直線)を生成
mr0 = Line(Point(xRange[0], 0), slope = sympy.oo )
mr1 = Line(Point(xRange[1], 0), slope = sympy.oo )
for i,m in enumerate(lines) :
p1 = (m.intersection(mr0))[0] # x=0 と 直線m の交点
p2 = (m.intersection(mr1))[0] # x=8 と 直線m の交点
plt.plot([p1.x, p2.x], [p1.y, p2.y])
plt.text( p2.x, p2.y, ' m{0}'.format(i), size = 10, verticalalignment='center')
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0],xRange[1]+1))
plt.yticks(range(yRange[0],yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
直線については、次のような値の取得や計算ができます。(3) は、直線を $ax + by + c = 0$ という式で表現したときの各係数をタプル $(a, b, c)$ で取得するものです。(4) のY軸との切片は、直接取得できなかったので係数から計算しています。
print(f'(1) type = {type(m0)}') # 型
print(f'(2) m0の傾き = {m0.slope}')
print(f'(3) m1の方程式の係数 = {m1.coefficients}')
intercept = lambda m: -m.coefficients[2] / m.coefficients[1]
print(f'(4) m1のY軸切片 = {intercept(m1)}')
print(f'(5) 直線m1 と m2 の交点 = {m1.intersection(m2)}')
(1) type = <class 'sympy.geometry.line.Line2D'>
(2) m0の傾き = 1/2
(3) m1の方程式の係数 = (2/3, 1, -22/3)
(4) m1のY軸切片 = 22/3
(5) 直線m1とm2の交点 = [Point2D(28/11, 62/11)]
Line からは equation により、sympy式を取得することができます。以下は、Lineから直線の式を取得して、$x$ に数値を代入して、$y$ について解いています(具体的には、直線m1について $x=4$ のときの $y$ の値を求めています)。
x, y = sympy.symbols('x y')
px = 4
py = sympy.solve(m1.equation(x,y).subs(x, px),y)[0]
print(f'直線m1 において、xが {px} のとき、yは {py} (={float(py):.1f}) となる')
直線m1 において、xが 4 のとき、yは 14/3 (=4.7) となる