(2019.08.21)1日ずらした相関図を追加。予測計算の部分は変更せず、1日ずらしの相関図作成部分を追加。まあまあの結果です。
(2019.08.24)月平均流量と年平均流量を表示するプログラムを追加。
(2019.09.03)月平均流量を表示するプログラムに月雨量表示を追加。
はじめに
「Python 流出解析用タンクモデルのプログラムを作ってみる」という記事で、タンクモデルのプログラムを作ってみたが、今回はモデルパラメータの自動検索を試みた。
「よく用いられている」とされている日流量解析用タンクモデルは、4段型で、1段(最上段)目に5個、2段めに3個、3段目に3個、4段目に1個もしくは2個、合計12あるいは13個のパラメータの入力が必要である。これは初期残留深さを除いた個数であり、初期残留深さを加えれば+4個のパラメータが存在する。このため、雨量データから流出量を計算する場合、最初に仮定したパラメータを入力し、実測流量を、より良く再現できるよう、パラメータの修正を行い、モデルを決定する。各タンクからの流出量は上部タンクからの流出の影響を受けるため、実測データと比較しながらパラメータを定めるのには労力がかかるが、その方法は、以下の文献などに紹介されている。
上記はタンクモデル開発者による論文であり、これを参考にしながらも、自己流でタンクモデルのモデルパラメータ検索に挑戦する。
方法論
できるだけ単純な方法を指向する観点から、ここで紹介する(思いついた)手法では以下の特色を持たせている。
-
- 各タンクに対しパラメータの補正係数は1つのみとする。すなわち4段タンクモデルには4個の補正係数を準備する
-
- タンクパラメータの補正に関して、タンクからの流量を増やしたい場合、側方流出係数は大きく、流出口位置は低く、下部への浸透流出係数は小さくする必要がある。これに対し各タンクに1つしか補正係数を準備していないので、乗算あるいは除算のみでパラメータの補正を行う。加算・減算はパラメータが負になる恐れがあるので用いない。
-
- 目標を流況曲線の再現におき、流況曲線を用いてパラメータ補正係数を算定する
-
- 流況曲線をタンクの数だけ分割しているが、分割比率は決められないので、乱数によりこれを仮定し、計算回数を増やすことにより、最適値を検索している。
準備するデータ
タンクモデルへの入力データとしての日雨量時系列と、モデルパラメータ同定のための実測日平均流量時系列を準備する。
モデル
モデルは4段モデルとし、パラメータの初期値は標準モデルより選定する。ここでは初期貯留量は既知の値とする。この事例では解析開始が1月1日であり、対象地域は雨季なので、流出口高さまで初期に貯留されているものと仮定する。
パラメータを収束させるための基本的な考え方
仮定したパラメータから流量予測を行い、ターゲットである実測流量との流量比からパラメータの補正量を算出し、これを前回パラメータに乗じることにより、補正されたパラメータを算出、これを用いて流量予測を行うというステップを繰り返す。
パラメータ補正の考え方
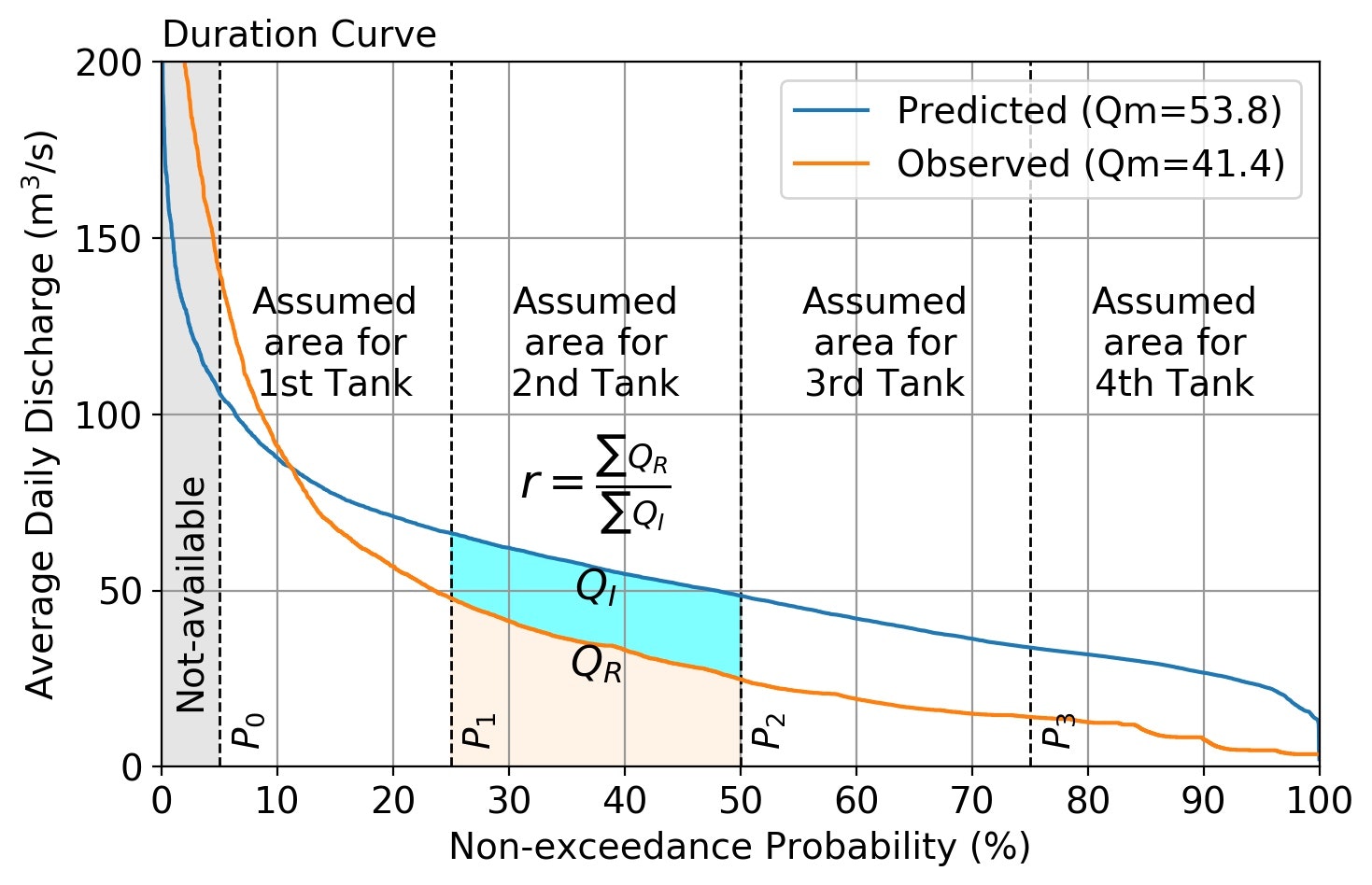
流況図の利用と区間分割
雨量から算定した日平均流量を実測流量に近似させたいことから、パラメータ補正には流況図を用いることとする。タンクは4段で構成されているが、第1段タンク(最上段)は流況図の高流量領域、第4段タンク(最下段)は流況図の低流量領域に、2段目・3段目は流況図の中間領域の流量に、より大きな影響を与えることが予想できる。このため流況図を、流量の非超過確率により4つの領域に分割し、それぞれの領域に、高流量から低流量域に向かい、第1段タンクから第4段タンクを割り当て、各領域の試算流量とターゲット流量(実測流量)との流量比により、各タンクのパラメータを修正する。なお、日流量解析では日最大流量再現には主眼を置かないため、ごく高流量域(非超過確率 $P_0$ 以下)は、補正係数の計算領域から除外している。なお、実際には各タンクが影響を及ぼす流量領域の非超過確率値を決めることはできない。このため、非超過確率の境界値($P_1$, $P_2$, $P_3$)は乱数により仮定してパラメータ推定・流量予測を繰り返し、ターゲットとの誤差が最小となるケースをパラメータの最適値とする。プログラム中では、指定した数値 [$P_0$+1 から 97 まで] から、random.choice でランダムに3個の整数を選び出し、これをソートして $P_1$, $P_2$, $P_3$ に当てはめており、毎回少しづつ異なる値が求まります。
パラメータ補正
仮定したパラメータによる流況図の各領域における予測流量を $Q_I$、実測流量を $Q_R$ とし、補正係数rを $r = \frac{\sum Q_R}{\sum Q_I}$ と定義する。もし仮定したパラメータによる予測流量が、実測流量より大きければ、予測流量が小さくなるようパラメータを補正してやれば良い。このため、各パラメータに対し以下の補正を行うことにする。ここに、$P$ の添字 $n$ は非超過確率の境界を示し、各パラメータの添字 $i$ は繰り返し回数を示す。
\begin{align}
& r_i=\cfrac{\sum_{P_n}^{P_{n+1}} Q_R}{\sum_{P_n}^{P_{n+1}} Q_{I(i)}} & & \text{補正係数}\\
& a_{1(i+1)}=a_{1(i)}*r_i & & \text{下側流出口流出係数}\\
& h_{1(i+1)}=\cfrac{h_{1(i)}}{r_i} & & \text{下側流出口高さ}& \\
& a_{2(i+1)}=a_{2(i)}*r_i & & \text{上側流出口流出係数}\\
& h_{2(i+1)}=\cfrac{h_{2(i)}}{r_i} & & \text{上側流出口高さ}\\
& b_{(i+1)}=\cfrac{b_{(i)}}{r_i} & & \text{浸透(底部)流出口流出係数}
\end{align}
流出係数 a1 および a2 の補正について
例えば、予測流量 $Q_I$ がターゲット流量 $Q_R$ より大きい場合、補正係数 $r$ は1より小さくなる。この場合、そのタンクでの予測流量を小さくするようパラメータを補正したいので、各流出係数に補正係数 $r$ を乗じることにより、次回繰り返しステップでの予測流量を小さくするよう補正する。
流出口高さ h1 および h2、浸透流出口流出係数 b の補正について
上記と同様、予測流量を小さくするようパラメータを補正する場合、$h_1$、$h_2$、$b$ を大きくすれば次回繰り返しステップでの予測流量は小さくなることが期待される。このため、各係数を補正係数 $r$ で除してやることにより、次回繰り返しステップの予測流量を小さくするよう補正する。
出力事例
パラメータ初期値
Case-1:火山灰地帯(1)
para[0,:]=np.array([0.100, 15, 0.100, 60, 0.200, 15]) # タンク1
para[1,:]=np.array([0.030, 30, 0.000, 999, 0.060, 30]) # タンク2
para[2,:]=np.array([0.006, 60, 0.000, 999, 0.012, 50]) # タンク3
para[3,:]=np.array([0.001, 0, 0.000, 999, 0.001, 0]) # タンク4
Case-2:火山灰地帯(2)
para[0,:]=np.array([0.050, 15, 0.050, 60, 0.200, 15]) # タンク1
para[1,:]=np.array([0.020, 30, 0.000, 999, 0.080, 30]) # タンク2
para[2,:]=np.array([0.004, 60, 0.000, 999, 0.016, 50]) # タンク3
para[3,:]=np.array([0.001, 0, 0.000, 999, 0.001, 0]) # タンク4
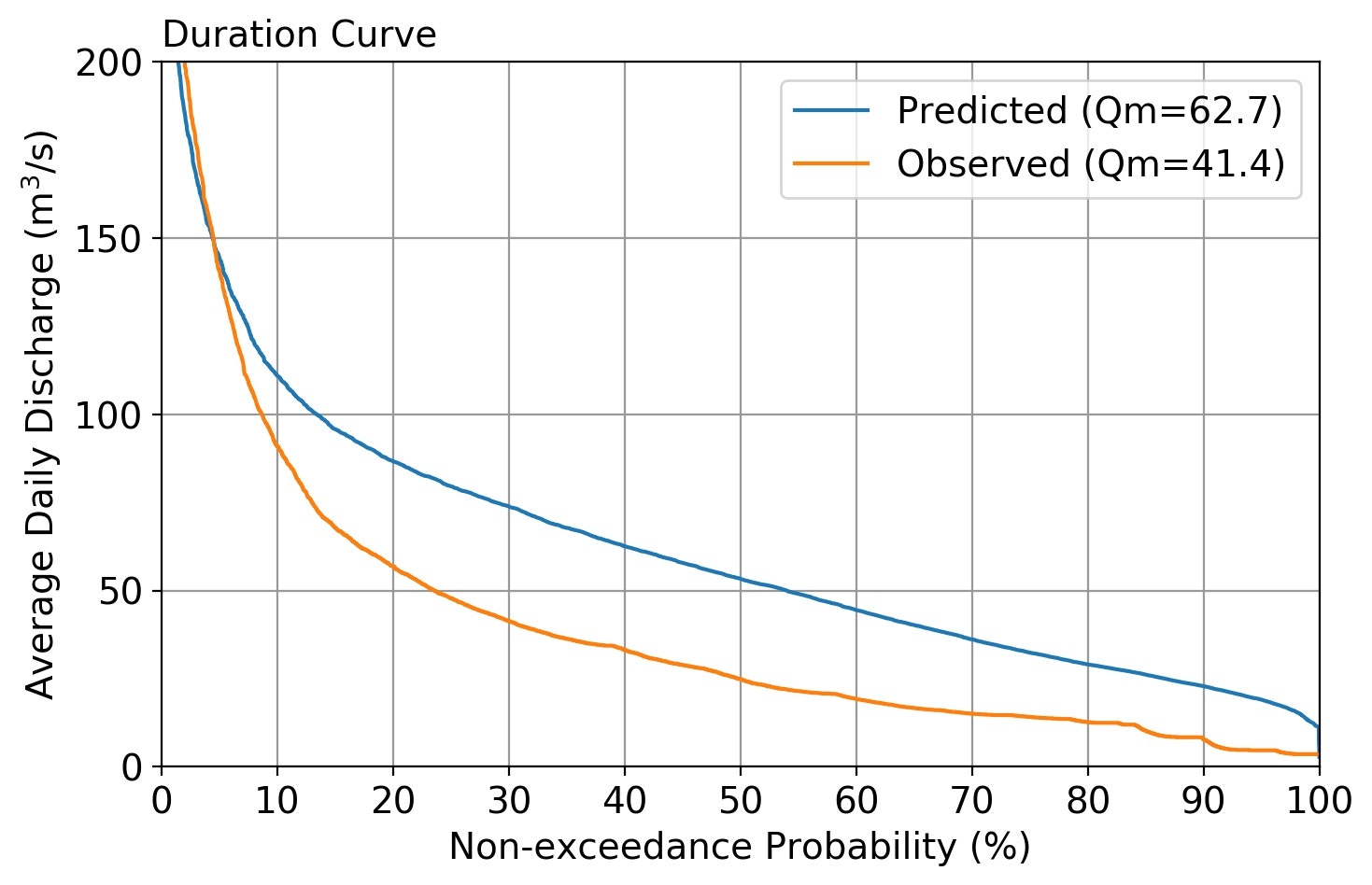
| パラメータ初期値による流量予測(Case-1) | パラメータ初期値による流量予測(Case-2) |
|---|---|
|
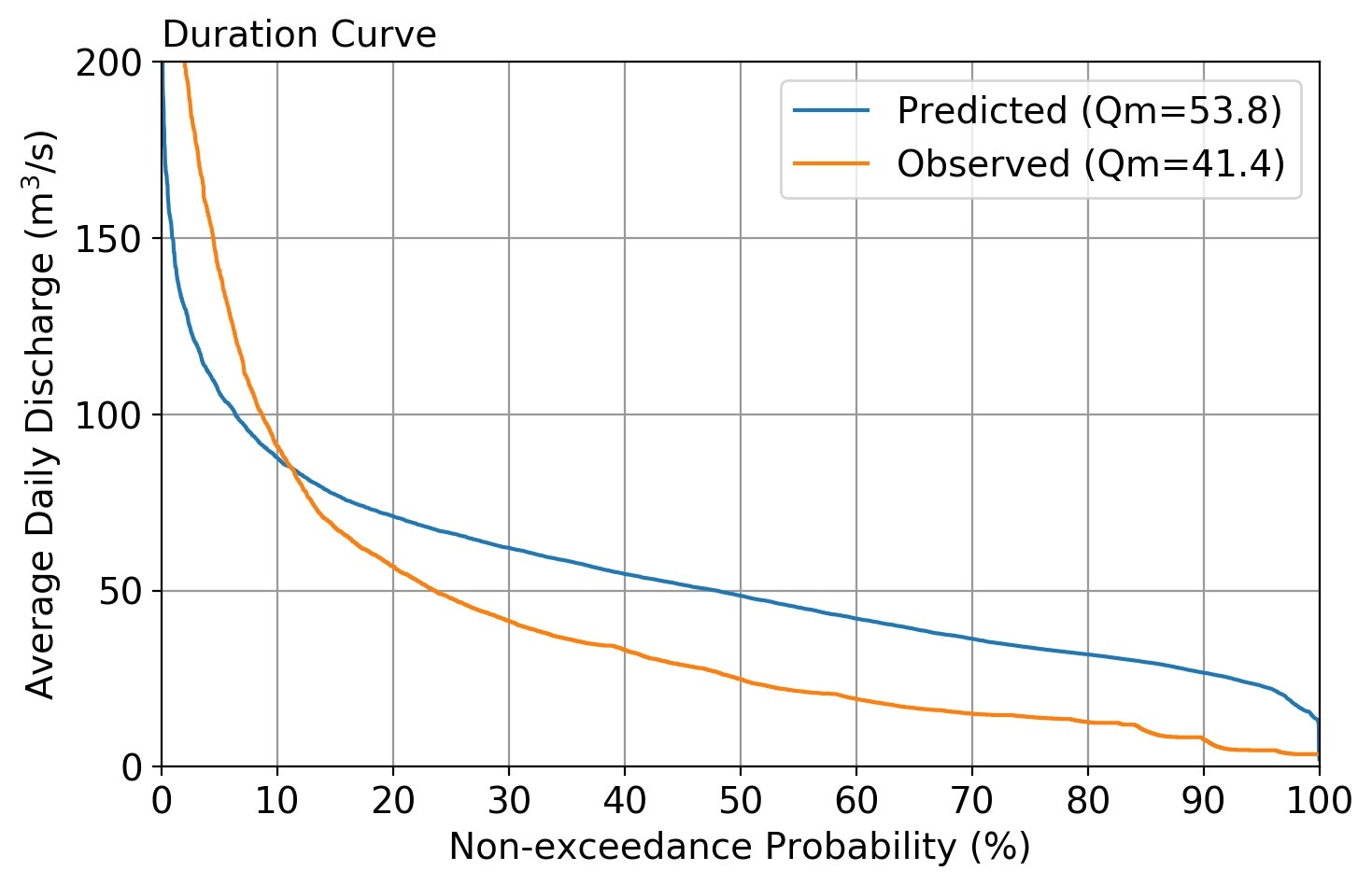
|
修正されたパラメータでの流量予測結果は以下の通り。上図に示す初期値をいれたものからみれば、ターゲットに近づいていることがわかります。
| 最終的な流量予測結果(Case-1) | 最終的な流量予測結果(Case-2) |
|---|---|
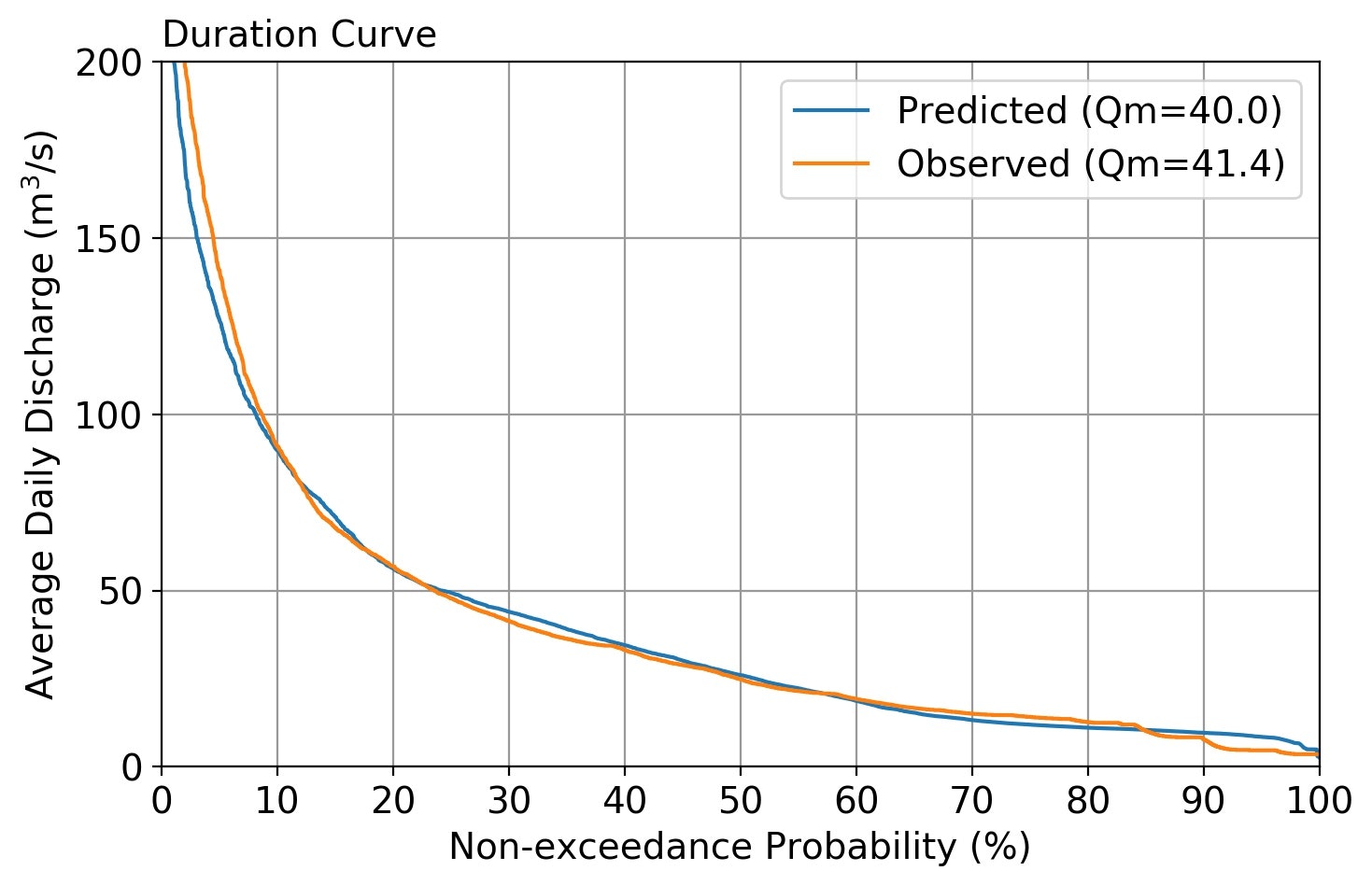
|
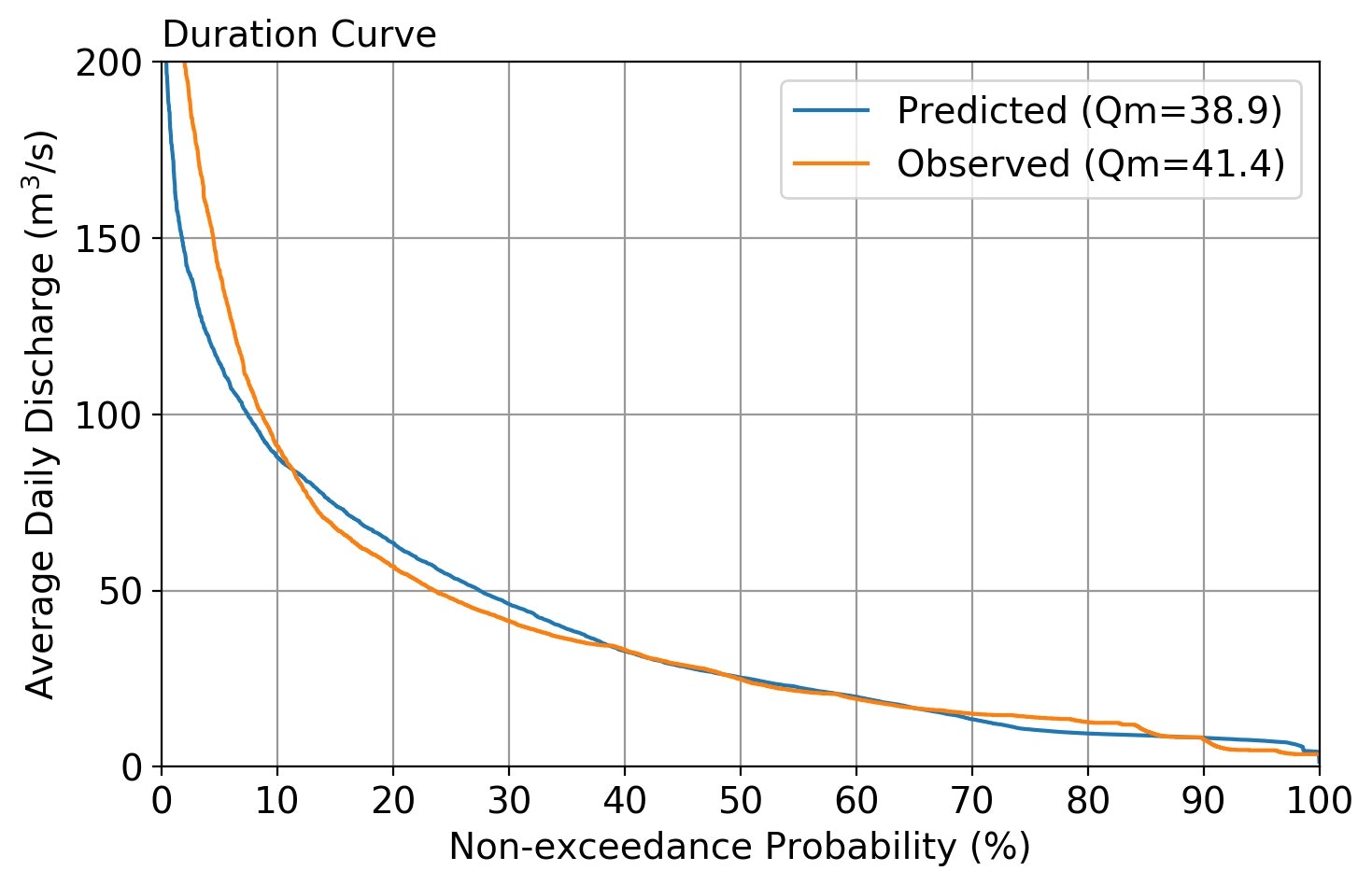
|
| 同一日での流量比較(Case-1) | 同一日での流量比較(Case-2) |
|---|---|
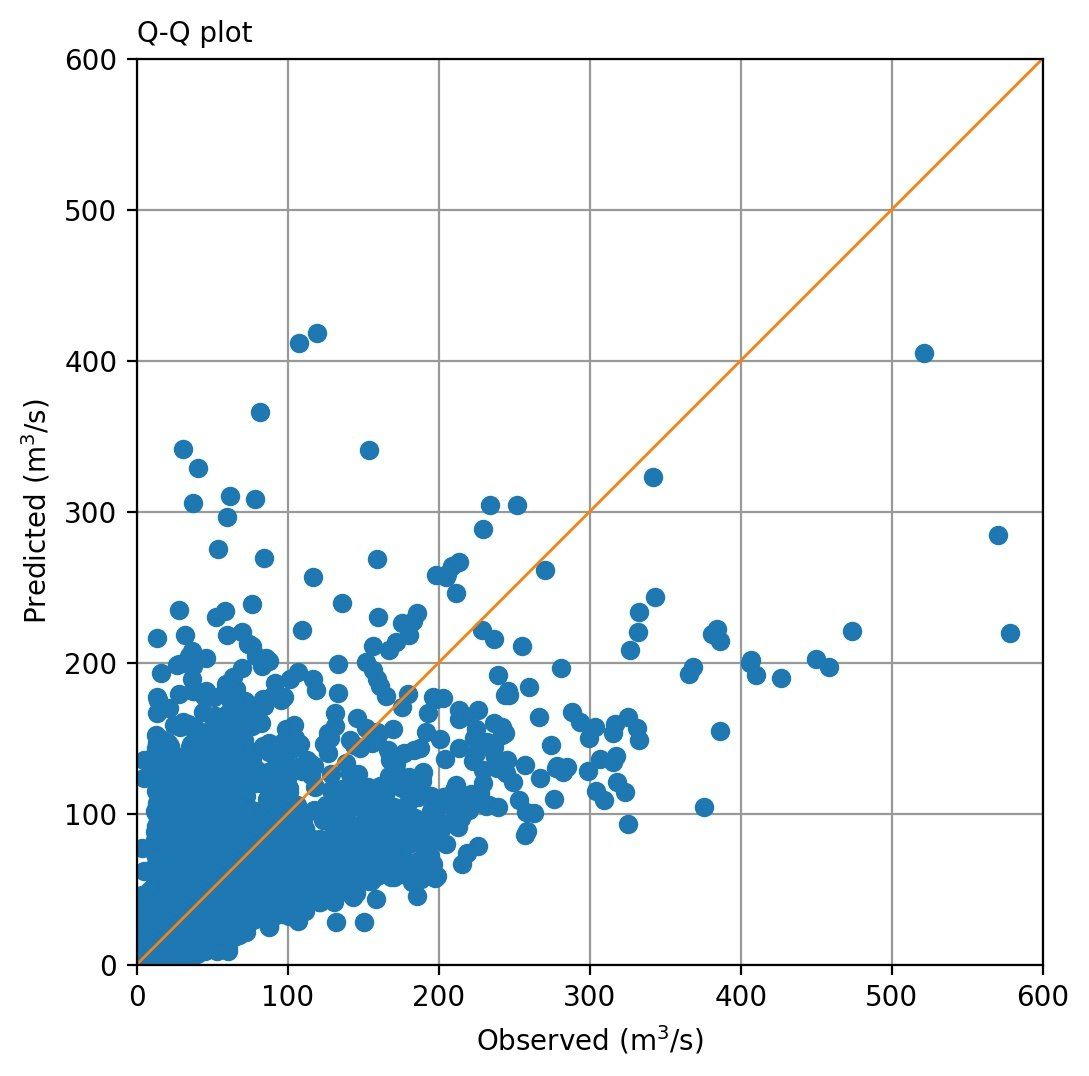
|
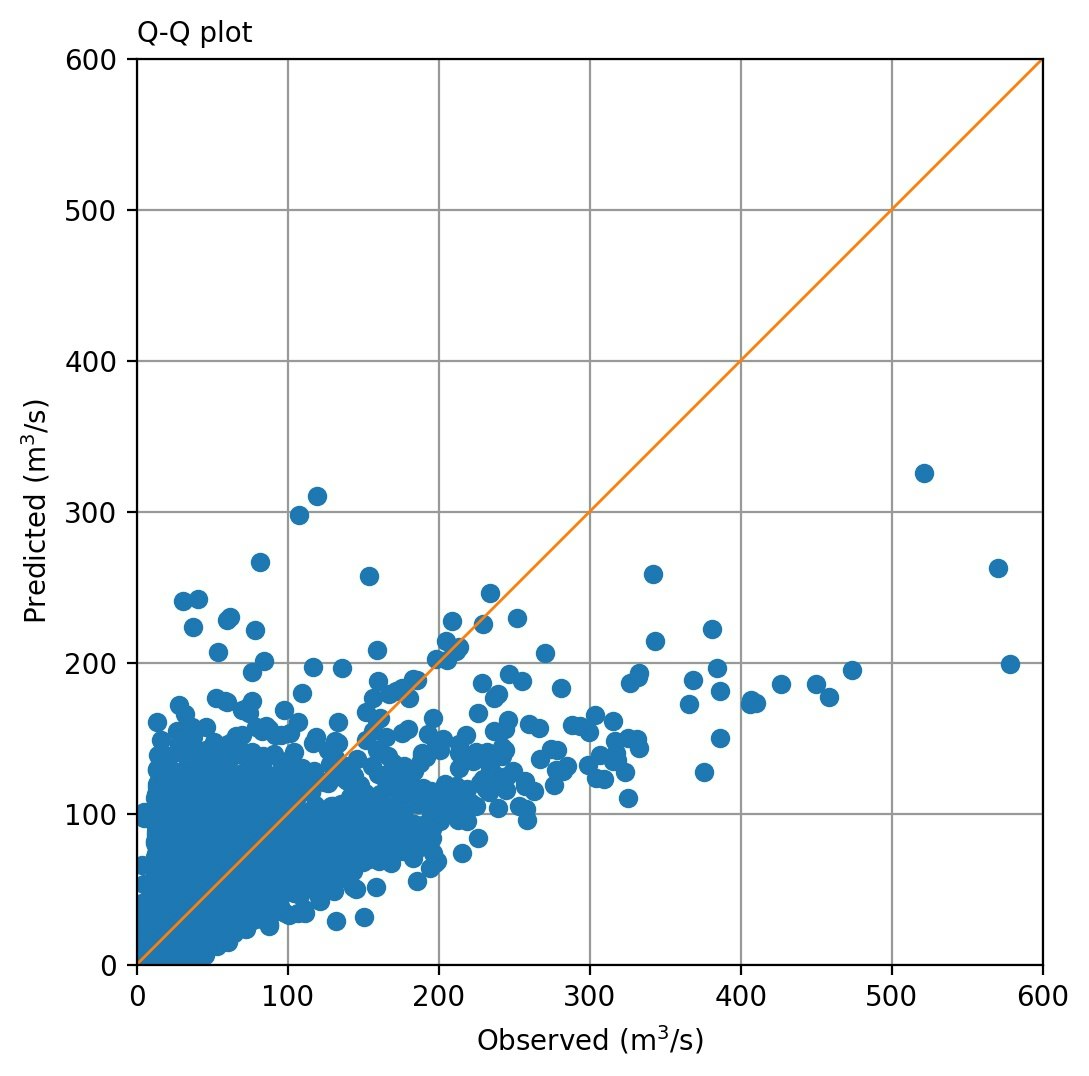
|
上図のように、ターゲットと予測値を同一日で比較するとかなり相関が悪い。流況図がそれなりに整合しているのだから、そんなことはないだろうということで、1日ずらした相関(当日の雨量に対して計算された予測値を翌日の流量とする)をとってみると下図のようになる。まあまあです。このことは、教科書*)にも、「日雨量から日流量を算出するとき、常に1日の遅れを与える」として示されています。ただモデルの特性のせいか、Case-2では全体的に流量が低く出る傾向が目立っています。このへんは初期値の工夫で改善できそうです。
*) 菅原正巳,水文学講座7 流出解析法,1973年10月15日初版2刷 共立出版株式会社
| 1日遅れでの流量比較(Case-1) | 1日遅れでの流量比較(Case-2) |
|---|---|
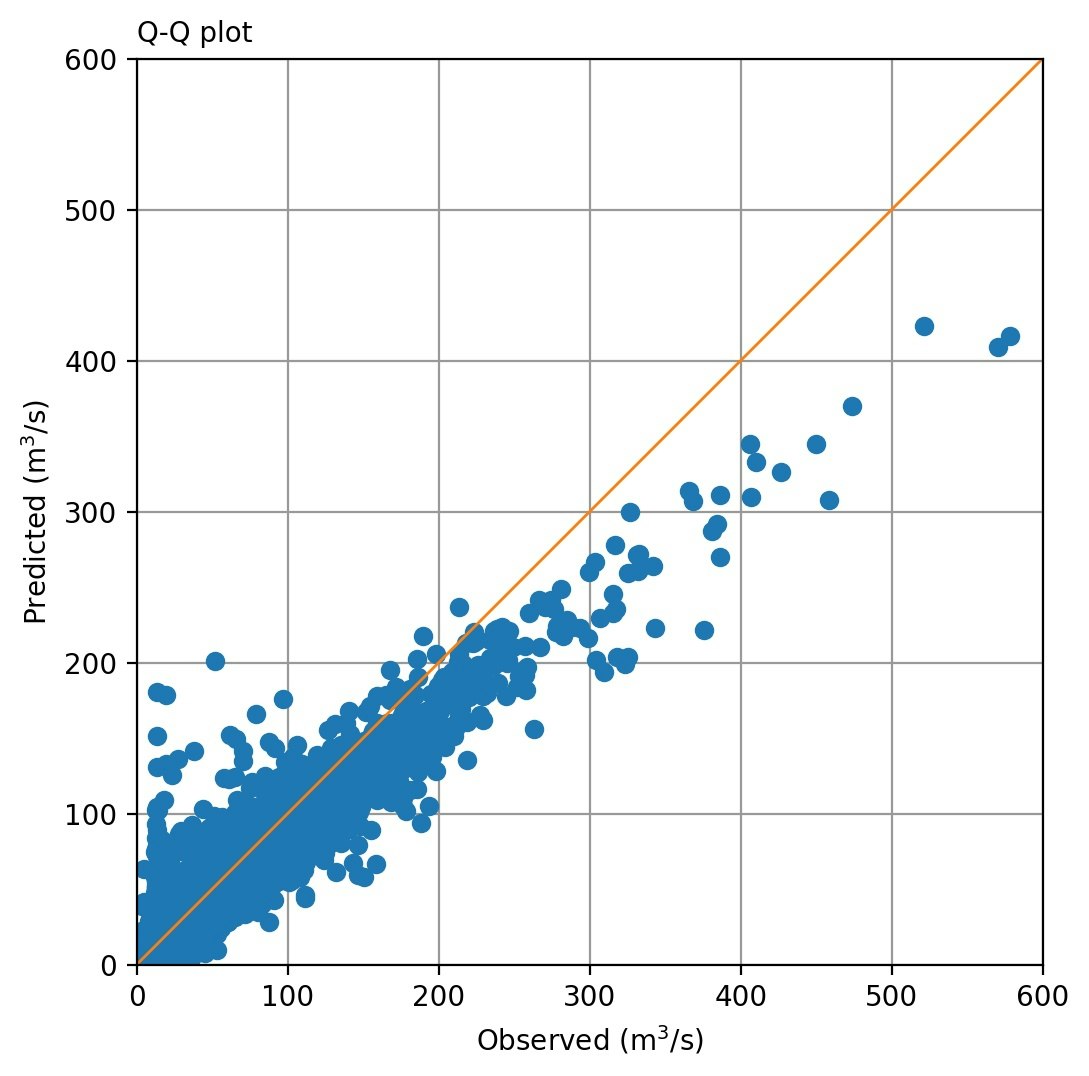
|
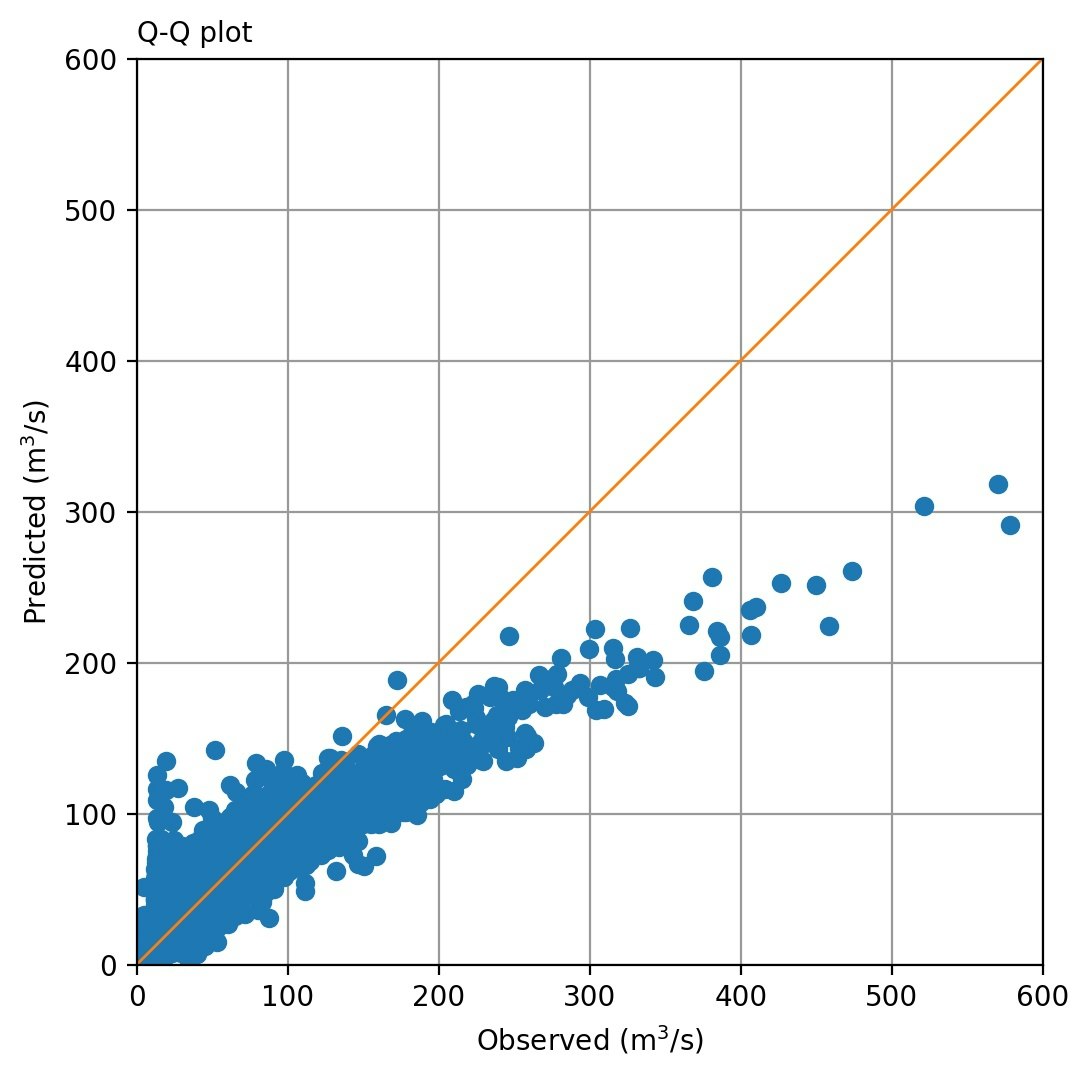
|
選定されたパラメータ
Case-1
* Comparison of Discharge
Case Qave Qmax Qmin
Observed 41.4 578.1 3.6
Predicted 40.0 418.1 2.6
* Estimated parameter
Tank No a1 h1 a2 h2 b ri
1st tank 0.1145 13.1043 0.1145 52.4171 0.1747 15.0000
2nd tank 0.0148 60.7691 0.0000 999.0000 0.1215 30.0000
3rd tank 0.0027 135.6202 0.0000 999.0000 0.0271 50.0000
4th tank 0.0005 0.0000 0.0000 999.0000 0.0020 0.0000
Case-2
* Comparison of Discharge
Case Qave Qmax Qmin
Observed 41.4 578.1 3.6
Predicted 38.9 325.2 1.5
* Estimated parameter
Tank No a1 h1 a2 h2 b ri
1st tank 0.0740 10.1329 0.0740 40.5316 0.1351 15.0000
2nd tank 0.0115 52.2659 0.0000 999.0000 0.1394 30.0000
3rd tank 0.0018 136.4676 0.0000 999.0000 0.0364 50.0000
4th tank 0.0005 0.0000 0.0000 999.0000 0.0021 0.0000
Case-1 での月平均流量と年平均流量の確認
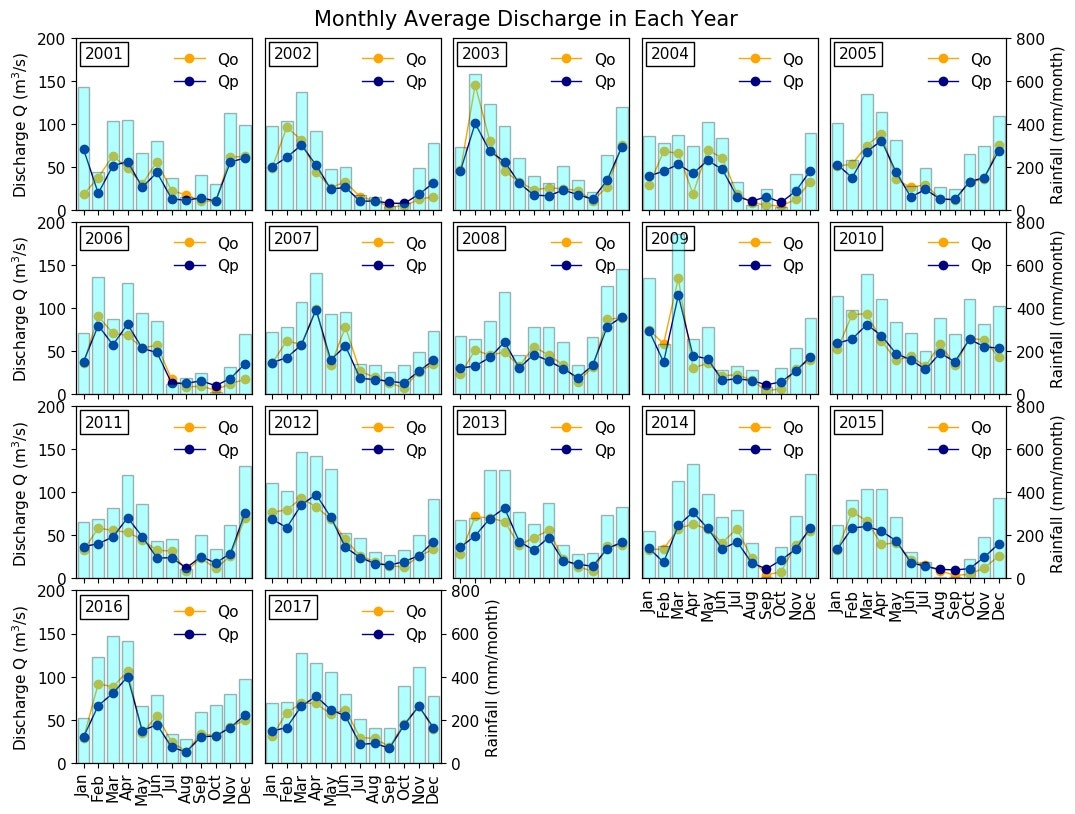
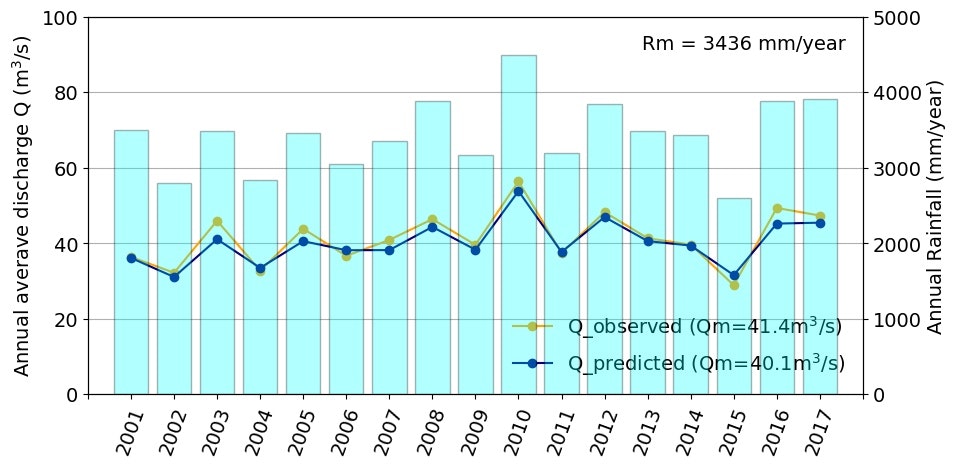
降雨日の1日遅れ予測流量が、ターゲット流量とまずまずの相関があることが確認できたし、流況図もまずまず再現できていることがわかったが、念の為、月平均流量と年平均流量が、ターゲットを再現できているか確認してみた。
年平均流量が、前述の事例と違うが、このグラフを作成するのに何回かプログラムを走らせているので、乱数により選定している各タンクに分担させる流量の非超過確率の違いによるもの。
月平均流量の比較
年平均流量の比較
タンクモデルプログラム
# パラメータ自動推定
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.ticker as tick
from scipy import interpolate
import numpy.random as random
def fig_duration(ppp, qqq, qq0, fnameF):
fsz=14
xmin=0; xmax=100; dx=10
ymin=0; ymax=200; dy=50
plt.figure(figsize=(8,5),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
tstr='Duration Curve'
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Non-exceedance Probability (%)')
plt.ylabel('Average Daily Discharge (m$^3$/s)')
plt.xticks(np.arange(xmin,xmax+dx,dx))
plt.yticks(np.arange(ymin,ymax+dy,dy))
plt.grid(color='#999999',linestyle='solid')
plt.title(tstr,loc='left',fontsize=fsz)
plt.plot(ppp,qqq,'-', label='Predicted (Qm={0:.1f})'.format(np.mean(qqq)))
plt.plot(ppp,qq0,'-', label='Observed (Qm={0:.1f})'.format(np.mean(qq0)))
plt.legend(loc='upper right')
plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
plt.show()
def fig_correlation(qo, qe, fnameF):
fsz=10
xmin=0; xmax=600; dx=100
ymin=0; ymax=600; dy=100
plt.figure(figsize=(6,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
tstr='Q-Q plot'
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Observed (m$^3$/s)')
plt.ylabel('Predicted (m$^3$/s)')
plt.xticks(np.arange(xmin,xmax+dx,dx))
plt.yticks(np.arange(ymin,ymax+dy,dy))
plt.grid(color='#999999',linestyle='solid')
plt.gca().set_aspect('equal',adjustable='box')
plt.title(tstr,loc='left',fontsize=fsz)
plt.plot(qo,qe,'o')
plt.plot([xmin,xmax],[ymin,ymax],'-',lw=1)
plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
plt.show()
def inp_rf():
# input rainfall data
fnameR='rf_karaena.csv'
df = pd.read_csv(fnameR, header=0, index_col=0)
df.index = pd.to_datetime(df.index, format='%Y-%m-%d')
df=df[df.index >= '2001-01-01'] # data after 2001-01-01 is available
return df
def inp_tank():
# ca : catchment area (km2)
# eva : evaporation (mm/day)
# nt : number of tanks
# para = [a1, h1, a2, h2, b, r_ini]
# a1 : discharge coefficient of the first outlet
# h1 : height of the first outlet
# a2 : discharge coefficient of the second outlet
# h2 : height of the second outlet
# b : discharge coefficient of the bottom outlet
# r_ini : initial value of the storage depth (residual depth)
ca=822.6
eva=-10
nt=4
para=np.zeros((nt, 6))
para[0,:]=np.array([0.100, 15, 0.100, 60, 0.200, 15])
para[1,:]=np.array([0.030, 30, 0.000, 999, 0.060, 30])
para[2,:]=np.array([0.006, 60, 0.000, 999, 0.012, 50])
para[3,:]=np.array([0.001, 0, 0.000, 999, 0.001, 0])
#para[0,:]=np.array([0.050, 15, 0.050, 60, 0.200, 15])
#para[1,:]=np.array([0.020, 30, 0.000, 999, 0.080, 30])
#para[2,:]=np.array([0.004, 60, 0.000, 999, 0.016, 50])
#para[3,:]=np.array([0.001, 0, 0.000, 999, 0.001, 0])
return nt, para, ca, eva
def cal_tank(rfj, r_i, a1, h1, a2, h2, b):
# rfj : rainfall
# r_i : residual depth
# x_i : storage depth
# y_i : runoff depth
# z_i : infiltratio
x_j = r_i + rfj
if 0 < x_j:
if x_j <= h1 : y_j = 0
if h1 < x_j and x_j <= h2: y_j = a1 * (x_j - h1)
if h2 < x_j : y_j = a1 * (x_j - h1) + a2 * (x_j - h2)
z_j = b * x_j
r_j = x_j - y_j - z_j
else:
x_j = 0
y_j = 0
z_j=x_j
r_j=0
return x_j, y_j, z_j, r_j
def calc(nt, para, ca, eva, rf):
xx=np.zeros(nt, dtype=np.float64)
yy=np.zeros((nt, len(rf)), dtype=np.float64)
zz=np.zeros((nt, len(rf)), dtype=np.float64)
for ii in range(0, nt): # iteration for tank number
#print('* Tank-'+str(ii+1))
a1 =para[ii, 0] # run-off coefficient of lower outlet
h1 =para[ii, 1] # height of upper outlet
a2 =para[ii, 2] # run-off coefficient of upper outlet
h2 =para[ii, 3] # height of upper outlet
b =para[ii, 4] # run-off coefficient of bottom outlet
r_i=para[ii, 5] # initial storage (residual storage)
if ii==0:
rfl=rf # input rainfall to 1st tank
jj=np.where(rfl<=0) # if no-rainfall,
rfl[jj]=eva # evaporation is inputted
else:
rfl=zz[ii-1,:] # input discharge from upper tank botom outlet for 2nd tank or lower
#print('{0:>8s}{1:>8s}{2:>8s}{3:>8s}{4:>8s}'.format('rfj', 'r_i', 'x_j', 'y_j', 'z_j'))
for j, rfj in enumerate(rfl):
x_j, y_j, z_j, r_j = cal_tank(rfj, r_i, a1, h1, a2, h2, b)
#print('{0:8.2f}{1:8.2f}{2:8.2f}{3:8.2f}{4:8.2f}'.format(rfj, r_i, x_j, y_j, z_j))
r_i=r_j
yy[ii, j]=y_j
zz[ii, j]=z_j
xx[ii]=x_j
qq=np.zeros(len(rf), dtype=np.float64)
for j in range(0,len(rf)):
qq[j] = np.sum(yy[:, j])/1000*ca*1e6/24/3600 # (m3/s)
return qq, xx
def probdata(ppp, qq):
qp=np.sort(qq)[::-1]
ii=np.arange(len(qp))
pp=ii/(len(qp)-1)*100
ff=interpolate.interp1d(pp,qp)
qqq=ff(ppp)
return qqq
def main():
fig1='fig_auto1a.jpg'
fig2='fig_auto2a.jpg'
fig3='fig_auto3a.jpg'
fig4='fig_auto4a.jpg'
df0 = inp_rf() # input data
q0 = df0['kuroki'].values # target discharge
rf = df0['Dam'].values # rainfall
ppp=np.arange(0,len(df0)+1,dtype=np.float64)/len(df0)*100 # propability
qq0 = probdata(ppp, q0) # duration curve of taret discharge
nt, para, ca, eva = inp_tank() # input model parameter
qq, xx = calc(nt, para, ca, eva, rf) # run-off analysis
qqq = probdata(ppp, qq) # duration curve of predicted discharge
fig_duration(ppp, qqq, qq0, fig1) # draw duration curve
jmax=50 # maximum number of iteration
p0=5 # minimum probability considered
num=np.arange(p0+1, 98, 1) # range of boundary on duration curve
err0=np.sqrt(np.sum((qqq-qq0)**2)) # calculation of initial error factor
param=para # initial value of parameter memoried
coef=0.98 # correction factor for ratio
kkk=0
for jjj in range(jmax):
for i in range(100): # difinition of boundary on duration curve
arr=random.choice(num, 3, replace=False) # choice the 3 values of boundary
par=np.sort(arr)
p1=par[0] # lower limit of influence area of 1st tank
p2=par[1] # lower limit of influence area of 2nd tank
p3=par[2] # lower limit of influence area of 3rd tank
if 2<p2-p1 and 2<p3-p2: break
k0=np.where((p0 <= ppp) & (ppp < 100)) # index of whole range considered
k1=np.where((p0 <= ppp) & (ppp < p1)) # index of 1st tank influence area
k2=np.where((p1 <= ppp) & (ppp < p2)) # index of 2nd tank influence area
k3=np.where((p2 <= ppp) & (ppp < p3)) # index of 3rd tank influence area
k4=np.where((p3 <= ppp) & (ppp < 100)) # index of 4th tank influence area
# re-difinition of initial tank parameter and reference discharge
nt, para, ca, eva = inp_tank()
qq, xx = calc(nt, para, ca, eva, rf)
qqq = probdata(ppp, qq)
ratio = np.zeros(nt, dtype=np.float64) # array declaration of correction factors
imax=10 # maximum number of iteration
er0=err0 # initial value of error factor
eps=0.05 # allowable error
for iii in range(imax):
ratio[0]=np.sum(qq0[k1])/np.sum(qqq[k1]) # correction factor for 1st tank
ratio[1]=np.sum(qq0[k2])/np.sum(qqq[k2]) # correction factor for 2nd tank
ratio[2]=np.sum(qq0[k3])/np.sum(qqq[k3]) # correction factor for 3rd tank
ratio[3]=np.sum(qq0[k4])/np.sum(qqq[k4]) # correction factor for 4th tank
ratio=ratio*coef # correction factor for total shape
# parameter correction
# 1st tank
para[0,0]=para[0,0]*ratio[0]
para[0,1]=para[0,1]/ratio[0]
para[0,2]=para[0,2]*ratio[0]
para[0,3]=para[0,3]/ratio[0]
para[0,4]=para[0,4]/ratio[0]
# 2nd tank
para[1,0]=para[1,0]*ratio[1]
para[1,1]=para[1,1]/ratio[1]
para[1,4]=para[1,4]/ratio[1]
# 3rd tank
para[2,0]=para[2,0]*ratio[2]
para[2,1]=para[2,1]/ratio[2]
para[2,4]=para[2,4]/ratio[2]
# 4th tank
para[3,0]=para[3,0]*ratio[3]
para[3,4]=para[3,4]/ratio[3]
# calculation of reference discharge using corrected parameters
qq, xx = calc(nt, para, ca, eva, rf)
qqq = probdata(ppp, qq)
er1=np.sqrt(np.sum((qqq[k0]-qq0[k0])**2)) # calculation of error factor
if np.abs((er0-er1)/er0) < eps:
break
else:
er0=er1
err1=er1
print('{0:4d}{1:10.1f}{2:10.1f}{3:10.1f}{4:4d}{5:4d}'
.format(jjj, err1, err0, np.mean(qqq), iii, kkk)) # print of reference information
if err1 < err0:
param=para
err0=err1
kkk=jjj
print('{0:4d}{1:10.3f}'.format(kkk, err0))
qq, xx = calc(nt, param, ca, eva, rf)
print('Last xx = ', xx)
qqq = probdata(ppp, qq)
fig_duration(ppp, qqq, qq0, fig2)
i0=np.where(rf<0)
rf[i0]=0
df1 = pd.DataFrame({'date' : df0.index.values,
'Rf' : rf,
'Qo' : q0,
'Qp' : qq})
df1 = df1.set_index('date')
df1.to_csv('df1.csv')
print(df1)
print('* Comparison of Discharge')
print('{0:10s}{1:>8s}{2:>8s}{3:>8s}'.format('Case' ,'Qave','Qmax','Qmin'))
print('{0:10s}{1:8.1f}{2:8.1f}{3:8.1f}'.format('Observed' ,np.mean(qq0),np.max(qq0),np.min(qq0)))
print('{0:10s}{1:8.1f}{2:8.1f}{3:8.1f}'.format('Predicted',np.mean(qqq),np.max(qqq),np.min(qqq)))
print('* Estimated parameter')
print('{0:10s}{1:>10s}{2:>10s}{3:>10s}{4:>10s}{5:>10s}{6:>10s}'
.format('Tank No','a1','h1','a2','h2','b','ri'))
ss=['1st tank','2nd tank','3rd tank','4th tank']
for i in range(nt):
print('{0:10s}{1:10.4f}{2:10.4f}{3:10.4f}{4:10.4f}{5:10.4f}{6:10.4f}'
.format(ss[i],param[i,0],param[i,1],param[i,2],param[i,3],param[i,4],param[i,5]))
# Correlation between same days
qo=q0
qe=qq
fig_correlation(qo, qe, fig3)
# Correlation between a day and previous day
n=len(q0)
qo=q0[1:n]
qe=qq[0:n-1]
fig_correlation(qo, qe, fig4)
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
月平均流量と年平均流量描画プログラム
雨量と流量の年変化を描画するプログラムで、凡例を装飾する以下の2つが効いてないみたいです。なんででしょう?
plt.rcParams['legend.facecolor']='#ffffff'
plt.rcParams['legend.framealpha']=1
プログラム
# Outline of flow data
import numpy as np
import pandas as pd
import datetime
import matplotlib.pyplot as plt
import seaborn as sns
# global
_ylist=np.arange(2001,2018,1)
ylist=[]
for y in _ylist:
ylist=ylist+[str(y)]
def rdata():
df = pd.read_csv('df1.csv', header=0, index_col=0)
df.index = pd.to_datetime(df.index, format='%Y-%m-%d')
#df=df[df.index >= '2001-01-01']
rf=df['Rf']
q0=df['Qo']
q1=df['Qp']
d= df.index
rfl=pd.Series(np.array(rf),index=d)
qq0=pd.Series(np.array(q0),index=d)
qq1=pd.Series(np.array(q1),index=d)
return rfl, qq0, qq1
def makedf(qq):
# discharge data
mlist=['-01','-02','-03','-04','-05','-06','-07','-08','-09','-10','-11','-12']
n=len(ylist)
m=len(mlist)
qt=np.zeros((n+1,m+1),dtype=np.float64) # sum of discharges of a month
ct=np.zeros((n+1,m+1),dtype=np.int) # sum of days of a manth
for i,sy in enumerate(ylist):
for j,sm in enumerate(mlist):
sym=sy+sm
qd=np.array(qq[sym])
ii=np.where(0<qd)
qt[i,j]=np.sum(qd[ii])
ct[i,j]=len(qd[ii])
for i in range(n):
qt[i,m]=np.sum(qt[i,0:m])
ct[i,m]=np.sum(ct[i,0:m])
for j in range(m):
qt[n,j]=np.sum(qt[0:n,j])
ct[n,j]=np.sum(ct[0:n,j])
qt[n,m]=np.sum(qt[0:n,0:m])
ct[n,m]=np.sum(ct[0:n,0:m])
dfq = pd.DataFrame({'Year': ylist+['Ave'],
'Jan' : qt[:,0]/ct[:,0],
'Feb' : qt[:,1]/ct[:,1],
'Mar' : qt[:,2]/ct[:,2],
'Apr' : qt[:,3]/ct[:,3],
'May' : qt[:,4]/ct[:,4],
'Jun' : qt[:,5]/ct[:,5],
'Jul' : qt[:,6]/ct[:,6],
'Aug' : qt[:,7]/ct[:,7],
'Sep' : qt[:,8]/ct[:,8],
'Oct' : qt[:,9]/ct[:,9],
'Nov' : qt[:,10]/ct[:,10],
'Dec' : qt[:,11]/ct[:,11],
'Ave': qt[:,12]/ct[:,12]})
dfq=dfq.set_index('Year')
return dfq
def makedfr(qq):
# rainfall data
mlist=['-01','-02','-03','-04','-05','-06','-07','-08','-09','-10','-11','-12']
n=len(ylist)
m=len(mlist)
qt=np.zeros((n+1,m+1),dtype=np.float64) # sum of discharges of a month
for i,sy in enumerate(ylist): # year
for j,sm in enumerate(mlist): # month
sym=sy+sm
qd=np.array(qq[sym])
ii=np.where(0<=qd)
qt[i,j]=np.sum(qd[ii])
for i in range(n):
qt[i,m]=np.sum(qt[i,0:m])
for j in range(m):
qt[n,j]=np.sum(qt[0:n,j])/len(ylist)
qt[n,m]=np.sum(qt[0:n,0:m])/len(ylist)
dfr = pd.DataFrame({'Year': ylist+['Ave'],
'Jan' : qt[:,0],
'Feb' : qt[:,1],
'Mar' : qt[:,2],
'Apr' : qt[:,3],
'May' : qt[:,4],
'Jun' : qt[:,5],
'Jul' : qt[:,6],
'Aug' : qt[:,7],
'Sep' : qt[:,8],
'Oct' : qt[:,9],
'Nov' : qt[:,10],
'Dec' : qt[:,11],
'Sum' : qt[:,12]})
dfr=dfr.set_index('Year')
return dfr
def figts(dfq0, dfq1, dfr):
# arrange of subplot
# ------------------------------------
# i= 0 i= 1 i= 2 i= 3 i= 4
# i= 5 i= 6 i= 7 i= 8 i= 9
# i=10 i=11 i=12 i=13 i=14
# i=15 i=16
# ------------------------------------
icol=5
irow=4
fsz=11
xx=np.array([1,2,3,4,5,6,7,8,9,10,11,12])
xx=xx-0.5
mlist=['Jan','Feb','Mar','Apr','May','Jun','Jul','Aug','Sep','Oct','Nov','Dec']
emp=['']*12
plt.figure(figsize=(12,12/icol*irow),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
plt.suptitle('Monthly Average Discharge in Each Year', x=0.5,y=0.91,fontsize=fsz+4)
plt.subplots_adjust(wspace=0.07,hspace=0.07)
for i,sy in enumerate(ylist):
# plot data
y0 = dfq0.loc[sy][0:12] # observed discharge
y1 = dfq1.loc[sy][0:12] # predicted discharge
yy = dfr.loc[sy][0:12] # rainfall
num=i+1
plt.subplot(irow,icol,num)
xmin=0;xmax=12
ymin=0;ymax=200
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
if i==0 or i==5 or i==10 or i==15:
plt.ylabel('Discharge Q (m$^3$/s)')
else:
plt.yticks([])
if i==13 or i==14 or i==15 or i==16:
plt.xticks(xx,mlist,rotation=90)
else:
plt.xticks(xx,emp,rotation=90)
plt.plot(xx,y0,'o-',color='#ffa500',lw=1,label='Qo')
plt.plot(xx,y1,'o-',color='#000080',lw=1,label='Qp')
props = dict(boxstyle='square', facecolor='#ffffff', alpha=1)
xs=xmin+0.05*(xmax-xmin); ys=ymin+0.95*(ymax-ymin)
plt.text(xs,ys, sy, fontsize=fsz,va='top',ha='left', bbox=props)
plt.legend()
plt.twinx()
ymin=0; ymax=800; dy=200
plt.ylim([ymin,ymax])
if i==4 or i==9 or i==14 or i==16:
plt.ylabel('Rainfall (mm/month)')
else:
plt.yticks([])
plt.bar(xx,yy,color="#00ffff", edgecolor="#000000", alpha=0.3, linewidth=1)
fnameF='fig_thm_tank.jpg'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
def figyy(dfq0, dfq1, dfr):
# plot data
xx=np.zeros(len(ylist), dtype=np.float64)
y0=np.zeros(len(ylist), dtype=np.float64)
y1=np.zeros(len(ylist), dtype=np.float64)
yy=np.zeros(len(ylist), dtype=np.float64)
for i, sy in enumerate(ylist):
xx[i] = float(sy) # year
y0[i] = dfq0.loc[sy][12] # ovserved annual discharge
y1[i] = dfq1.loc[sy][12] # predicted annual discharge
yy[i] = dfr.loc[sy][12] # annual rainfall
ave0 = dfq0.loc['Ave'][12] # average ovserved discharge
ave1 = dfq1.loc['Ave'][12] # average predicted discharge
aver = dfr.loc['Ave'][12] # average rainfall
fsz=14
xmin=float(ylist[0])-1
xmax=float(ylist[len(ylist)-1])+1
plt.figure(figsize=(10,5), facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
plt.rcParams['legend.frameon']=False
plt.rcParams['legend.facecolor']='#ffffff'
plt.rcParams['legend.framealpha']=1
ymin=0; ymax=100
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.ylabel('Annual averave discharge Q (m$^3$/s)')
locs = np.arange(xmin,xmax+1,1)
xtick=['']+ylist+['']
plt.xticks(locs, xtick, color='#000000', fontsize=fsz, rotation=70)
plt.plot(xx,y0,'o-',color='#ffa500',label='Q_observed (Qm={0:.1f}m$^3$/s)'.format(ave0))
plt.plot(xx,y1,'o-',color='#000080',label='Q_predicted (Qm={0:.1f}m$^3$/s)'.format(ave1))
plt.grid(axis='y')
plt.legend(loc='lower right').get_frame().set_alpha(1.0)
plt.twinx()
ymin=0; ymax=5000; dy=1000
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.ylabel('Annual Rainfall (mm/year)')
plt.bar(xx,yy,color="#00ffff", edgecolor="#000000", alpha=0.3, linewidth=1)
tstr='Rm = {0:.0f} mm/year'.format(aver)
plt.legend(loc='upper right', title=tstr)
fnameF='fig_thy_tank.jpg'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
def main():
rfl, qq0, qq1 = rdata()
dfq0 = makedf(qq0)
dfq1 = makedf(qq1)
dfr = makedfr(rfl)
pd.options.display.precision = 1
pd.set_option("display.width", 200)
print('* Observed')
print(dfq0)
print()
print('* Predicted')
print(dfq1)
print()
print('* Rainfall')
print(dfr)
figts(dfq0, dfq1, dfr)
figyy(dfq0, dfq1, dfr)
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
以 上