はじめに
昔からタンクモデルの勉強をしたかったのだが、直接的な動機が無かったため手つかずでいた。しかし、最近、流出解析に触れる機会があったので、ここぞとばかりにタンクモデルのプログラムを作ってみようと思い立った。
タンクモデルとは、菅原正巳氏により提案されたモデルであり、側方および底部に流出口を有するタンクを複数個、組み合わせることにより、降雨の表層流出・地盤内への浸透流出などの挙動を表現する、流出解析用モデルである。通常、比較的長期流出を対象とする日流量解析では4段、短期流出を対象とする洪水流量解析では2段のタンクモデルが用いられている。
主要部分のプログラムは、その昔は「手計算でやっていた」(文献1による) ものをプログラム化しただけなので、単純である。プログラムを作っていじってみると、単純な物理モデルの組み合わせで色々な流況が表現でき、先人の偉大さを思うと共に、とても楽しい。難点はパラメータが多いことだが、洪水解析用・日流量解析用に標準的なパラメータが準備されており、それを使うだけでもかなりの近似ができる。これからも色々いじってみたいものだ。
なお、この記事は「水文学とは何か? 流出解析とは何か?」を論じるものではなく、純粋にプログラムを作って回すことを目的としたものである。
文献(教科書)
-
- 菅原正巳,水文学講座7 流出解析法,1973年10月15日初版2刷 共立出版株式会社
-
- 菅原正巳・渡辺一郎・尾崎睿子・勝山ヨシ子,パーソナル・コンピュータのためのタンク・モデル・プログラムとその使い方,国立防災科学技術センター研究報告 第37号 1986年3月
計算式
以下に示す計算式およびその説明は、文献 (1) を筆者なりに理解した(つもりの)内容を書いている。なお、モデルにおいては、雨量・流量などの物理量は全て単位底面積を持つタンク(容器)内の水深(単位:mm)で表現される。
(モデル概念図:第1タンク)

(計算式)
ある時刻の貯留高 $x_j$ は、前ステップでの残高 $r_{j-1}$ に雨量 $R_j$ を加えたものとする。残高 $r$ は、貯留高・雨量に対し前ステップでの値となるので、計算開始時には初期値として与える必要がある。
\begin{equation}
x_j = r_{j-1} + R_j
\end{equation}
流出高 $y_j$、浸透高 $z_j$、残高 $r_j$ の計算は以下により行う。各物理量の計算は、蒸発の扱いを考慮して、貯留高 $x_j$ の符号により場合分けして行う。
In case of $0 < x_j$,
\begin{align}
&y_j =
\begin{cases}
0 & (x_j < h_1) \\
\alpha_1\cdot(x_j - h_1) & (h_1 \leqq x_j \leqq h_2) \\
\alpha_1\cdot(x_j - h_1) + \alpha_2\cdot(x_j - h_2) & (h_2 < x_j)
\end{cases}\\
&z_j = \beta \cdot x_j \\
&r_j = x_j - y_j - z_j
\end{align}
In case of $x_j \leqq 0$,
\begin{align}
&y_j = 0 \\
&z_j = x_j \\
&r_j = 0
\end{align}
\begin{align}
&R_j & &\text{雨量 (mm/hr) or (mm/day)}\\
&x_j & &\text{貯留高 (mm/hr) or (mm/day)}\\
&y_j & &\text{流出高 (mm/hr) or (mm/day)}\\
&z_j & &\text{浸透高 (mm/hr) or (mm/day)}\\
&r_j & &\text{残高 (mm/hr) or (mm/day)}\\
&\alpha_1 & &\text{下段流出口流出係数}\\
&h_1 & &\text{下段流出口高さ (mm)}\\
&\alpha_2 & &\text{上段流出口流出係数}\\
&h_2 & &\text{下段流出口高さ (mm)}\\
&\beta & &\text{浸透流出口流出係数}\\
\end{align}
(説明)
計算時刻は、雨量 $R$ の入力時刻に等しい時刻とする。すなわち、雨量の入力単位は、mm/hr あるいは mm/day なので、通常の計算時間単位は、1 hr あるいは 1 day となる。
最初の式(再掲)
\begin{equation}
x_j = r_{j-1} + R_j
\end{equation}
において、第1タンク(最上段)での入力は、雨量 $R$ となるが、第2タンク以下では、
雨量の代わりに上側タンクからの浸透高 $z$ を上式 $R$ の代わりに用いる。
蒸発量を考慮する場合は、上式の雨量 $R$ に蒸発を示す負の値を入力する。この場合、上式の残高 $r_{j-1}$ が小さければ、貯留高 $x_j$ が負の値になる場合があるので、$x_j$ が正の場合と負の場合に分けて計算を行う。
貯留高 $x_j$ が負の場合は、流出高および残留高をゼロにセットし、浸透高に負の貯留高を与え、下側のタンクの入力としてやれば良い。
入力データ
\begin{align}
&\text{モデルパラメータ}& &\alpha_1 & &\text{下段流出口流出係数}\\
& & &h_1 & &\text{下段流出口高さ (mm)}\\
& & &\alpha_2 & &\text{上段流出口流出係数}\\
& & &h_2 & &\text{下段流出口高さ (mm)}\\
& & &\beta & &\text{浸透流出口流出係数}\\
&\text{時系列解析データ}& &R & &\text{雨量時刻歴 (mm/hr) or (mm/day)}\\
& & &r_0 & &\text{残高初期値 (mm)}\\
\end{align}
流出係数
(設定の考え方)
流出係数は、大きくなれば流出が早く貯留高の減少も早くなる。この貯留高の減少速度を表す指標として、時定数を考える。タンクモデルでの流出係数は、時定数が以下のようになるよう定めることを基本とする。
| タンク | 時定数 Tc | 流出形態 |
|---|---|---|
| 第1タンク | 1〜数日 | 表面流出(surface discharge) |
| 第2タンク | 数日〜10日 | 中間流出(intermediate discharge) |
| 第3タンク | 1〜数ヶ月 | 準基底流出(sub-base discharge) |
| 第4タンク | 1〜数年 | 基底流出(base discharge) |
時定数 $T_c$ の値は、以下で計算できる。
T_c \doteqdot \cfrac{1}{\alpha + \beta}
ここに、$\alpha$ は流出口流出係数、$\beta$ は浸透流出口流出係数である。
上式より、各タンクの、$\alpha + \beta$ の値の目安は、以下のようになる。
| 時定数 Tc | α+β |
|---|---|
| 2 days | 0.5 |
| 10 days | 0.1 |
| 30 days | 0.03 |
| 365 days | 0.003 |
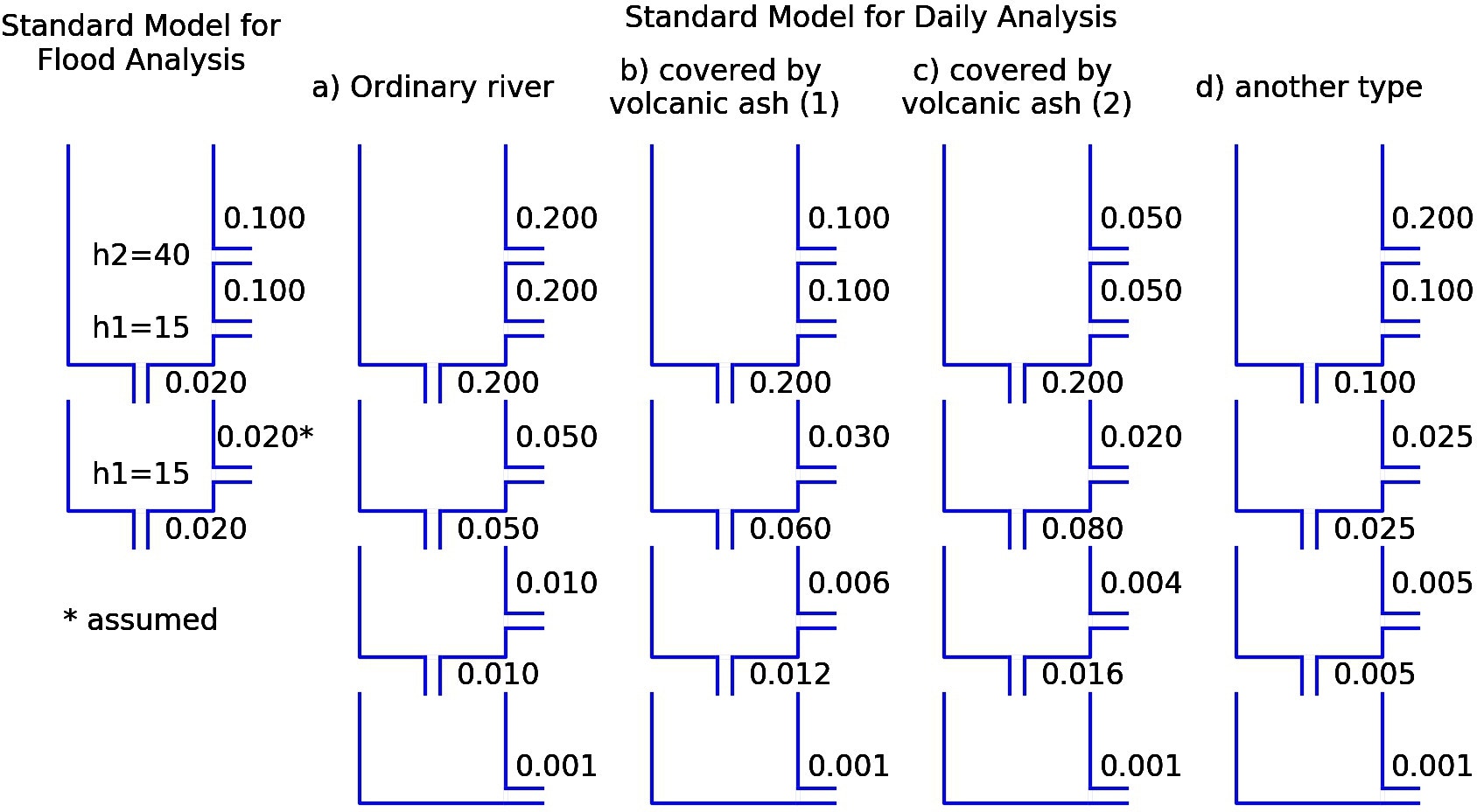
(標準モデル)
文献 2) に記載されている、各流出口の $\alpha$、$\beta$ の値を紹介する。
下図は、各流出口の係数を示したもの。洪水解析用モデル(左端)2段目タンクの流出係数 $\alpha$ は文献の記載が抜けているため推定値を表示している。
流出口高さ
流出口高さ $h$ の初期値の標準値は、下表に示すとおり、文献 2) に紹介されている。
| 流出口位置 | h (mm) |
|---|---|
| 第1タンク下側流出口 | 5〜15 |
| 第1タンク上側流出口 | 25〜60 |
| 第2タンク流出口 | 0〜30 |
| 第3タンク流出口 | 0〜60 |
| 第4タンク流出口 | 0 |
残高初期値
残高初期値 $r_0$ も計算開始時に与える必要がある。この値はとりあえず適当な数字(例えば0)を与えておき、計算評価対象開始日より数ヶ月前から計算を開始する、あるいは、1年分以上の予備計算を実施し、その結果から評価対象開始日近傍の値を入力するなどの方法で対処する。
プログラムと計算事例
1段タンクモデル
まずは単純な1段タンクモデルを考える。
ただプログラムとしては今後の拡張を考え、以下の構成とする。
| 関数名 | 役割 |
|---|---|
| inp_rf() | 雨量データ入力 |
| inp_tank() | 流域情報・モデルパラメータ入力 |
| cal_tank() | タンクモデルの計算(計算式の示した部分) |
| calc() | パラメータ・時刻歴計算の制御 |
| main() | 制御部呼び出し |
雨量データは、このモデルでは数少ないため、numpy配列に書き込んでいるが、実務的な日流量解析では数年から数十年のデータを扱うため、ファイル読む込みとなる。このため、関数書き換えを考慮して独立させてある。
流域情報・モデルパラメータとしては以下の項目を入力する。
| 変数 | 意味 |
|---|---|
| ca | 流域面積 (km2) |
| eva | 蒸発量 (mm/day) |
| nt | タンク段数 |
| a1 | 第1(下側)流出口流出係数 |
| h1 | 第1(下側)流出口高さ |
| a2 | 第2(上側)流出口流出係数 |
| h2 | 第2(上側)流出口高さ |
| b | 底部流出口流出係数 |
| r_ini | 初期残高(タンク内初期水位) |
各タンクの特性は、以下のようにタンク毎に numpy 配列で指定する。
para[i,:] = np.array([a1, h1, a2, h2, b, r_ini])
なお、このモデルでは蒸発は考慮していないし、流量への換算も行っていないが、入力項目は設定し、ダミーを入れてある。
実際のモデルは、文献(1)の、図82および表7に示されているものである。
プログラム
# 1段タンクモデル
import numpy as np
def inp_rf():
# Rainfall data
rf=np.array([8.0,3.5,0.1,21.7,27.8,15.6,43.2,5.2,0.1,0,0,0,0,0,0])
return rf
def inp_tank():
# ca : catchment area (km2)
# eva : evaporation (mm/day)
# nt : number of tanks
# para = [a1, h1, a2, h2, b, r_ini]
# a1 : discharge coefficient of the first outlet
# h1 : height of the first outlet
# a2 : discharge coefficient of the second outlet
# h2 : height of the second outlet
# b : discharge coefficient of the bottom outlet
# r_ini : initial value of the storage depth (residual depth)
ca=100
eva=0
nt=1
para=np.zeros((nt, 6))
para[0,:]=np.array([0.100, 15, 0.200, 40, 0.200, 0])
return nt, para, ca, eva
def cal_tank(rfj, r_i, a1, h1, a2, h2, b):
# rfj : rainfall
# r_i : residual depth
# x_i : storage depth
# y_i : runoff depth
# z_i : infiltration
x_j = r_i + rfj
if 0 < x_j:
if x_j <= h1: y_j = 0
if h1 <= x_j and x_j <= h2: y_j = a1 * (x_j - h1)
if h2 < x_j: y_j = a1 * (x_j - h1) + a2 * (x_j - h2)
z_j = b * x_j
r_j = x_j - y_j - z_j
else:
x_j = 0
y_j = 0
z_j=x_j
r_j=0
return x_j, y_j, z_j, r_j
def calc():
rf=inp_rf() # 雨量読み込み
nt, para, ca, eva=inp_tank() # モデルパラメータ・流域情報読み込み
ii=0
a1 =para[ii, 0] # 第1(下部)流出口流量係数
h1 =para[ii, 1] # 第1(下部)流出口高さ
a2 =para[ii, 2] # 第2(上部)流出口流量係数
h2 =para[ii, 3] # 第2(上部)流出口流量係数
b =para[ii, 4] # 底部流出口流量係数
r_i=para[ii, 5] # 初期残量(初期水位)
print('{0:>8s}{1:>8s}{2:>8s}{3:>8s}{4:>8s}'.format('rfj', 'r_i', 'x_j', 'y_j', 'z_j'))
for rfj in rf:
x_j, y_j, z_j, r_j = cal_tank(rfj, r_i, a1, h1, a2, h2, b)
print('{0:8.2f}{1:8.2f}{2:8.2f}{3:8.2f}{4:8.2f}'.format(rfj, r_i, x_j, y_j, z_j))
r_i=r_j
def main():
calc()
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
出力
rfj r_i x_j y_j z_j
8.00 0.00 8.00 0.00 1.60
3.50 6.40 9.90 0.00 1.98
0.10 7.92 8.02 0.00 1.60
21.70 6.42 28.12 1.31 5.62
27.80 21.18 48.98 5.19 9.80
15.60 33.99 49.59 5.38 9.92
43.20 34.30 77.50 13.75 15.50
5.20 48.25 53.45 6.53 10.69
0.10 36.22 36.32 2.13 7.26
0.00 26.93 26.93 1.19 5.39
0.00 20.35 20.35 0.53 4.07
0.00 15.74 15.74 0.07 3.15
0.00 12.52 12.52 0.00 2.50
0.00 10.02 10.02 0.00 2.00
0.00 8.01 8.01 0.00 1.60
3段タンクモデル(蒸発量考慮)
蒸発量を考慮した3段タンクモデルの計算例を示す。
- 複数段モデルの計算は、1段目・2段目・3段目と、下に向かって1段ずつ計算を進める。
- 2段目以下のタンクには、上部タンクからの浸透量(配列 zz に格納)を、最上部タンクの雨量に相当する入力として与える。
- 蒸発量は、雨量がゼロの日に、負の雨量として入力する(蒸発量は一定値とし、関数:inp_tank の中で変数 eva に格納している)。
計算に用いたモデルは、文献(1)の図84および表10に示されているものである。
プログラム
# 3段タンクモデル一般化(蒸発量考慮)
import numpy as np
def inp_rf():
# Rainfall data
rf=np.array([0, 3, 29, 23, 0, 0, 1, 9, 1, 0, 0, 0, 0, 0, 0, 1, 0, 6, 67, 0])
return rf
def inp_tank():
# ca : catchment area (km2)
# eva : evaporation (mm/day)
# nt : number of tanks
# para = [a1, h1, a2, h2, b, r_ini]
# a1 : discharge coefficient of the first outlet
# h1 : height of the first outlet
# a2 : discharge coefficient of the second outlet
# h2 : height of the second outlet
# b : discharge coefficient of the bottom outlet
# r_ini : initial value of the storage depth (residual depth)
ca=100
eva=-5
nt=3
para=np.zeros((nt, 6))
para[0,:]=np.array([0.100, 15, 0.200, 40, 0.200, 10])
para[1,:]=np.array([0.030, 15, 0.000, 9999, 0.020, 15])
para[2,:]=np.array([0.002, 0, 0.000, 9999, 0.000, 0])
return nt, para, ca, eva
def cal_tank(rfj, r_i, a1, h1, a2, h2, b):
# rfj : rainfall
# r_i : residual depth
# x_i : storage depth
# y_i : runoff depth
# z_i : infiltration
x_j = r_i + rfj
if 0 < x_j:
if x_j <= h1: y_j = 0
if h1 < x_j and x_j <= h2: y_j = a1 * (x_j - h1)
if h2 < x_j: y_j = a1 * (x_j - h1) + a2 * (x_j - h2)
z_j = b * x_j
r_j = x_j - y_j - z_j
else:
x_j = 0
y_j = 0
z_j=x_j
r_j=0
return x_j, y_j, z_j, r_j
def calc():
rf=inp_rf() # 雨量読み込み
nt, para, ca, eva=inp_tank() # モデルパラメータ・流域情報読み込み
yy=np.zeros((nt, len(rf)), dtype=np.float64)
zz=np.zeros((nt, len(rf)), dtype=np.float64)
for ii in range(0, nt): # タンクの段数だけ繰り返し
print('* Tank-'+str(ii+1))
a1 =para[ii, 0] # 第1(下部)流出口流量係数
h1 =para[ii, 1] # 第1(下部)流出口高さ
a2 =para[ii, 2] # 第2(上部)流出口流量係数
h2 =para[ii, 3] # 第2(上部)流出口流量係数
b =para[ii, 4] # 底部流出口流量係数
r_i=para[ii, 5] # 初期残量(初期水位)
if ii==0:
rfl=rf # 1段目(最上段)タンクには雨量を入力
jj=np.where(rfl<=0) # 雨量がゼロの日には
rfl[jj]=eva # 蒸発量を入力
else:
rfl=zz[ii-1,:] # 2段目以降のタンクには上部タンクの浸透量を入力
print('{0:>8s}{1:>8s}{2:>8s}{3:>8s}{4:>8s}'.format('rfj', 'r_i', 'x_j', 'y_j', 'z_j'))
for j, rfj in enumerate(rfl):
x_j, y_j, z_j, r_j = cal_tank(rfj, r_i, a1, h1, a2, h2, b)
print('{0:8.2f}{1:8.2f}{2:8.2f}{3:8.2f}{4:8.2f}'.format(rfj, r_i, x_j, y_j, z_j))
r_i=r_j
yy[ii, j]=y_j
zz[ii, j]=z_j
return 0
def main():
calc()
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
出力
* Tank-1
rfj r_i x_j y_j z_j
-5.00 10.00 5.00 0.00 1.00
3.00 4.00 7.00 0.00 1.40
29.00 5.60 34.60 1.96 6.92
23.00 25.72 48.72 5.12 9.74
-5.00 33.86 28.86 1.39 5.77
-5.00 21.70 16.70 0.17 3.34
1.00 13.19 14.19 0.00 2.84
9.00 11.35 20.35 0.54 4.07
1.00 15.75 16.75 0.17 3.35
-5.00 13.22 8.22 0.00 1.64
-5.00 6.58 1.58 0.00 0.32
-5.00 1.26 0.00 0.00 0.00
-5.00 0.00 0.00 0.00 0.00
-5.00 0.00 0.00 0.00 0.00
-5.00 0.00 0.00 0.00 0.00
1.00 0.00 1.00 0.00 0.20
-5.00 0.80 0.00 0.00 0.00
6.00 0.00 6.00 0.00 1.20
67.00 4.80 71.80 12.04 14.36
-5.00 45.40 40.40 2.62 8.08
* Tank-2
rfj r_i x_j y_j z_j
1.00 15.00 16.00 0.03 0.32
1.40 15.65 17.05 0.06 0.34
6.92 16.65 23.57 0.26 0.47
9.74 22.84 32.58 0.53 0.65
5.77 31.40 37.18 0.67 0.74
3.34 35.77 39.11 0.72 0.78
2.84 37.60 40.44 0.76 0.81
4.07 38.87 42.94 0.84 0.86
3.35 41.24 44.59 0.89 0.89
1.64 42.81 44.46 0.88 0.89
0.32 42.68 43.00 0.84 0.86
0.00 41.30 41.30 0.79 0.83
0.00 39.68 39.68 0.74 0.79
0.00 38.15 38.15 0.69 0.76
0.00 36.69 36.69 0.65 0.73
0.20 35.31 35.51 0.62 0.71
0.00 34.18 34.18 0.58 0.68
1.20 32.92 34.12 0.57 0.68
14.36 32.87 47.23 0.97 0.94
8.08 45.32 53.40 1.15 1.07
* Tank-3
rfj r_i x_j y_j z_j
0.32 0.00 0.32 0.00 0.00
0.34 0.32 0.66 0.00 0.00
0.47 0.66 1.13 0.00 0.00
0.65 1.13 1.78 0.00 0.00
0.74 1.78 2.52 0.01 0.00
0.78 2.51 3.30 0.01 0.00
0.81 3.29 4.10 0.01 0.00
0.86 4.09 4.95 0.01 0.00
0.89 4.94 5.83 0.01 0.00
0.89 5.82 6.71 0.01 0.00
0.86 6.70 7.56 0.02 0.00
0.83 7.54 8.37 0.02 0.00
0.79 8.35 9.14 0.02 0.00
0.76 9.13 9.89 0.02 0.00
0.73 9.87 10.60 0.02 0.00
0.71 10.58 11.29 0.02 0.00
0.68 11.27 11.95 0.02 0.00
0.68 11.93 12.61 0.03 0.00
0.94 12.59 13.53 0.03 0.00
1.07 13.50 14.57 0.03 0.00
少し実際的なモデル(4段タンク、蒸発量考慮)
少し実際的なモデルとして、蒸発量を考慮した4段タンクを考える。
やっていることの概要は以下の通り。
- 雨量データは、18年強の期間分があり、csv形式で格納されている。これを読み込み解析を行う。読み込みは、後処理の簡略化のため変数毎の配列ではなく、pandas のデータフレームとして読み込む。
- モデルパラメータとしては、標準モデルに示されている「Standard Model for Daily Analysis b) covered by volcanic ash (2)」を入力している。流出口高さは、標準値として示されている値の上限とした。ただし、対象区域は石灰岩地帯であるため、実測流量に合わせるため、最下段タンクにも浸透量(観測地点には流出せずどこかに流下してしまう分)を見込んでいる。
- 解析結果は、流量に換算し、「日付、雨量、流量」の形でデータフレームとしてcsv形式で出力する。プログラム内ではデータフレームが思ったようにできているか確認するため、最初の3行と最後の3行を出力させている。
- 書き出したcsvデータを別プログラムで読み込み、雨量と流量の経時変化図、流況図として画像出力する。
計算プログラム
# 複数段タンクモデル(蒸発散考慮)
import numpy as np
import pandas as pd
def inp_rf():
# input rainfall data
fnameR='rf_karaena.csv'
df = pd.read_csv(fnameR, header=0, index_col=0)
return df
def inp_tank():
# ca : catchment area (km2)
# eva : evaporation (mm/day)
# nt : number of tanks
# para = [a1, h1, a2, h2, b, r_ini]
# a1 : discharge coefficient of the first outlet
# h1 : height of the first outlet
# a2 : discharge coefficient of the second outlet
# h2 : height of the second outlet
# b : discharge coefficient of the bottom outlet
# r_ini : initial value of the storage depth (residual depth)
ca=822.6
eva=-10
nt=4
para=np.zeros((nt, 6))
para[0,:]=np.array([0.050, 15, 0.050, 60, 0.200, 0])
para[1,:]=np.array([0.020, 30, 0.000, 9999, 0.080, 0])
para[2,:]=np.array([0.004, 60, 0.000, 9999, 0.016, 0])
para[3,:]=np.array([0.001, 0, 0.000, 9999, 0.004, 0])
return nt, para, ca, eva
def cal_tank(rfj, r_i, a1, h1, a2, h2, b):
# rfj : rainfall
# r_i : residual depth
# x_i : storage depth
# y_i : runoff depth
# z_i : infiltration
x_j = r_i + rfj
if 0 < x_j:
if x_j <= h1: y_j = 0
if h1 < x_j and x_j <= h2: y_j = a1 * (x_j - h1)
if h2 < x_j: y_j = a1 * (x_j - h1) + a2 * (x_j - h2)
z_j = b * x_j
r_j = x_j - y_j - z_j
else:
x_j = 0
y_j = 0
z_j=x_j
r_j=0
return x_j, y_j, z_j, r_j
def calc():
df = inp_rf()
rf = df['Dam'].values
nt, para, ca, eva = inp_tank()
yy=np.zeros((nt, len(rf)), dtype=np.float64)
zz=np.zeros((nt, len(rf)), dtype=np.float64)
for ii in range(0, nt): # タンクの段数だけ繰り返し
a1 =para[ii, 0]
h1 =para[ii, 1]
a2 =para[ii, 2]
h2 =para[ii, 3]
b =para[ii, 4]
r_i=para[ii, 5]
if ii==0:
rfl=rf # 最上段タンクの入力に日雨量をセット)
jj=np.where(rfl<=0) # 日雨量がゼロの場合
rfl[jj] = eva # 雨量ベクトルに蒸発量をセット
else:
rfl=zz[ii-1,:] # 2段目以降のタンクには上川タンクからの浸透量を入力
for j, rfj in enumerate(rfl): # 逐次計算により各成分の時刻歴を求める
x_j, y_j, z_j, r_j = cal_tank(rfj, r_i, a1, h1, a2, h2, b)
r_i=r_j
yy[ii, j]=y_j
zz[ii, j]=z_j
qq=np.zeros(len(rf), dtype=np.float64)
for j in range(0,len(rf)):
qq[j] = np.sum(yy[:, j])/1000*ca*1e6/24/3600 # (m3/s)
df['Q']=qq
return df
def main():
df=calc()
df.to_csv('data_df.csv')
print(df.head(3))
print('......')
print(df.tail(3))
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
Dam Q
date
2000-03-01 0.2 4.874667e-07
2000-03-02 -10.0 1.413166e-06
2000-03-03 1.5 6.387978e-06
......
Dam Q
date
2017-12-29 4.0 50.685573
2017-12-30 -10.0 39.722776
2017-12-31 21.6 47.037735
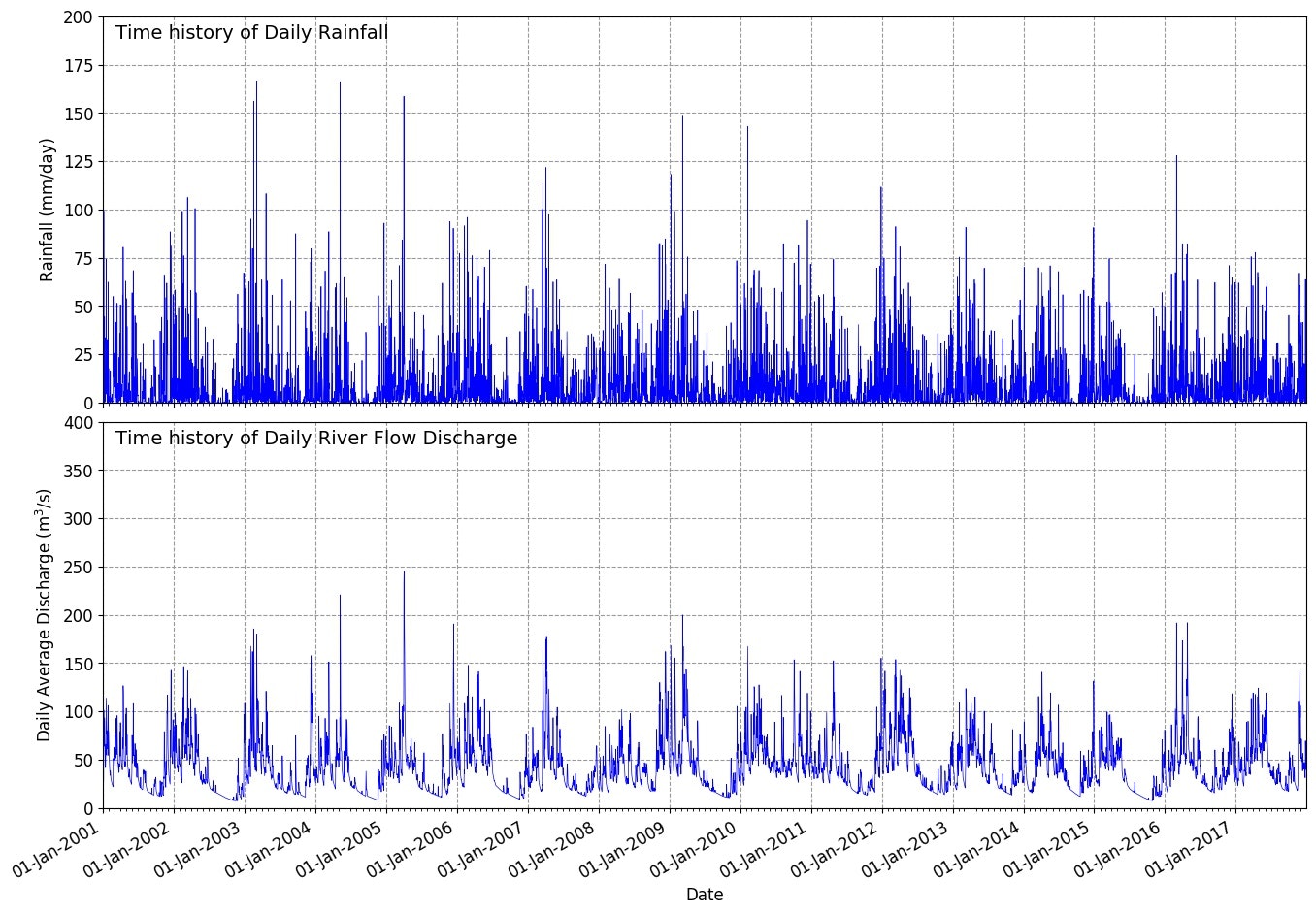
作図プログラム
やっていることは以下の通り。
- タンクモデルの計算で出力したcsvファイルをデータフレームとして読み込む。読み込んだデータの日付を日付型インデックスとして定義する。データフレームには2000年3月1日から2017年12月31日までの計算結果が格納されているが、流況図はきっちり1年づつで作成したいので、2001年1月1日以降のデータのみを有効にしている。
- 関数 drawfig() で雨量と流量の時系列図を描画する。
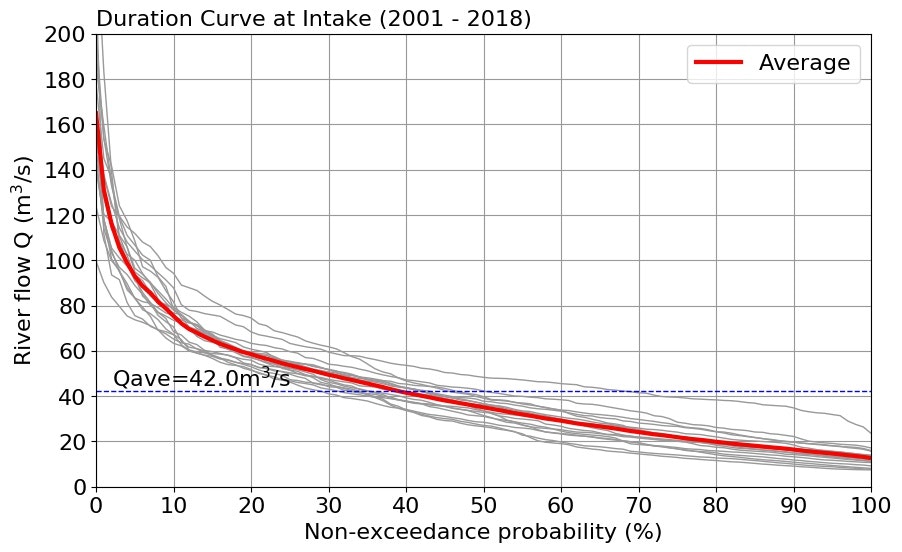
- 関数 makedata() で1年毎のデータを抽出し、大きい順(降順)で並び替え、1%単位で非超過確率の数値を与える。これは通常年と閏年を同一に扱うためと、%流量を簡単に抽出できるようにするための処理である。この関数に渡すデータは、日付と流量のみの Series としている。
- 関数 duration() で1年毎の流況曲線を描画する。グラフに描画した全平均は日超過確率1%単位に換算したものから計算しているので、入力されたデータフレームに格納されている生流量から計算した数値とは若干異なる。
時系列グラフの日付軸設定は、以下の記事を参照のこと。
Python matplotlib 時系列グラフ(時間軸の設定)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime
import matplotlib.dates as mdates
from scipy import interpolate
# global
tstr='Duration Curve at Intake (2001 - 2018)'
ylist=np.arange(2001,2018,1)
def drawfig(df):
# 経時変化図作成
fsz=12
plt.figure(figsize=(16,12),facecolor='w')
plt.rcParams['font.size']=fsz
plt.subplots_adjust(wspace=0, hspace=0.05)
sxmin='2001-01-01'
sxmax='2017-12-31'
xmin = datetime.datetime.strptime(sxmin, '%Y-%m-%d')
xmax = datetime.datetime.strptime(sxmax, '%Y-%m-%d')
# 雨量時刻歴作図
plt.subplot(211)
ymin=0; ymax=200
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Date')
plt.ylabel('Rainfall (mm/day)')
plt.grid(which='major',axis='both',color='#999999',linestyle='--')
plt.plot(df.index, df['Dam'], '-', lw=0.5, color='#0000ff', label='Rainfall')
ss='Time history of Daily Rainfall'
xs=xmin+0.01*(xmax-xmin); ys=ymin+0.98*(ymax-ymin)
plt.text(xs,ys,ss,color='#000000',ha='left',va='top',fontsize=fsz+2)
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=12))
plt.gca().xaxis.set_minor_locator(mdates.MonthLocator(interval=1))
# 流量時刻歴作図
plt.subplot(212)
ymin=0; ymax=400
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Date')
plt.ylabel('Daily Average Discharge (m$^3$/s)')
plt.grid(which='major',axis='both',color='#999999',linestyle='--')
plt.plot(df.index, df['Q'], '-', lw=0.5, color='#0000ff', label='River flow')
ss='Time history of Daily River Flow Discharge'
xs=xmin+0.01*(xmax-xmin); ys=ymin+0.98*(ymax-ymin)
plt.text(xs,ys,ss,color='#000000',ha='left',va='top',fontsize=fsz+2)
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%d-%b-%Y'))
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=12))
plt.gca().xaxis.set_minor_locator(mdates.MonthLocator(interval=1))
plt.gcf().autofmt_xdate()
# 画像保存
fnameF='fig_timehistory.jpg'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
def makedata(qq):
# 流況図作図用データフレーム作成
ylm=[]
for sy in ylist:
ssy=str(sy)
qd=np.array(qq[ssy])
if np.min(qd)<0:
print(ssy)
else:
ylm=ylm+[sy]
ppp=np.arange(0,101,dtype=np.float64) # propability
df = pd.DataFrame({'prob': ppp})
for i,sy in enumerate(ylm):
ssy=str(sy)
qd=np.array(qq[ssy])
qd=np.sort(qd)[::-1]
ii=np.arange(len(qd))
pp=ii/(len(qd)-1)*100
ff=interpolate.interp1d(pp,qd)
qqq=ff(ppp)
df[ssy]=qqq
df=df.set_index('prob')
df['ave']=df.mean(axis=1)
return df
def duration(df):
# 流況図作成
fsz=16
xmin=0; xmax=100; dx=10
ymin=0; ymax=200; dy=20
fig=plt.figure(figsize=(10,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Non-exceedance probability (%)')
plt.ylabel('River flow Q (m$^3$/s)')
plt.xticks(np.arange(xmin,xmax+dx,dx))
plt.yticks(np.arange(ymin,ymax+dy,dy))
plt.grid(color='#999999',linestyle='solid')
plt.title(tstr,loc='left',fontsize=fsz)
ly=df.columns.values # dfのカラム名をリストで取得
plt.plot(df.index,df[ly],'-',color='#999999',lw=1,label=None)
plt.plot(df.index,df[ly[-1]],'-',color='#ff0000',lw=3,label='Average')
qave=np.mean(df['ave']) # 平均流量の指定
plt.plot([xmin,xmax],[qave,qave],'--',color='#0000ff',lw=1)
xs=xmin+0.02*(xmax-xmin); ys=qave; ss='Qave={0:.1f}m$^3$/s'.format(qave)
plt.text(xs,qave,ss,ha='left',va='bottom',fontsize=fsz)
plt.legend()
fnameF='fig_duration.jpg'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
def main():
df = pd.read_csv('data_df.csv', header=0, index_col=0)
df.index = pd.to_datetime(df.index, format='%Y-%m-%d')
df=df[df.index >= '2001-01-01']
print(df.head(3))
print('......')
print(df.tail(3))
print(df.describe())
drawfig(df)
qq=pd.Series(np.array(df['Q']),index=df.index)
df=makedata(qq)
duration(df)
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
出力事例
Dam Q
date
2001-01-01 19.6 36.942847
2001-01-02 -10.0 27.405053
2001-01-03 6.4 28.021137
......
Dam Q
date
2017-12-29 4.0 50.685573
2017-12-30 -10.0 39.722776
2017-12-31 21.6 47.037735
Dam Q
count 6209.000000 6209.000000
mean 7.461765 41.667716
std 17.612616 26.982480
min -10.000000 7.454776
25% 0.200000 21.339176
50% 2.500000 36.120439
75% 11.400000 53.799014
max 166.600000 245.809425
以 上