概要
前回紹介した記事ではタンクモデルで雨量から流量予測を行ったが、これを機械学習で行ってみた。使用した機械学習のライブラリはscikit-learnである。
基本的にやっていることは重回帰分析であり、使った手法は以下のものである(import部分を表示)。
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.neighbors import KNeighborsRegressor
入力データ
雨量から流量予測を行う場合、入力に工夫が必要である。すなわち、流量はその日の雨量のみならず、前日あるいは前々日・・・というように、以前に降った雨の影響を受けていることは経験的に明らかである。このため、以下の2ケースの入力を考えた。
Case-1
| rf0 | 当日の雨量 |
| rf1 | 前日の雨量 |
| rf2 | 前々日の雨量 |
| ... | |
| rf10 | 10日前の雨量 |
入力データファイルのイメージ(Case-1)
date, rf0, rf1, rf2, rf3, rf4, rf5, rf6, rf7, rf8, rf9, rf10, Qo
2000/03/01, 0.2
2000/03/02, 0 , 0.2
2000/03/03, 1.5, 0 , 0.2
2000/03/04, 0 , 1.5, 0 , 0.2
2000/03/05, 0 , 0 , 1.5, 0 , 0.2
2000/03/06, 13.6, 0 , 0 , 1.5, 0 , 0.2
2000/03/07, 4.4, 13.6, 0 , 0 , 1.5, 0 , 0.2
2000/03/08, 0.2, 4.4, 13.6, 0 , 0 , 1.5, 0 , 0.2
2000/03/09, 1.7, 0.2, 4.4, 13.6, 0 , 0 , 1.5, 0 , 0.2
2000/03/10, 10.9, 1.7, 0.2, 4.4, 13.6, 0 , 0 , 1.5, 0 , 0.2
2000/03/11, 0 , 10.9, 1.7, 0.2, 4.4, 13.6, 0 , 0 , 1.5, 0 , 0.2, q1
2000/03/12, 0.9, 0 , 10.9, 1.7, 0.2, 4.4, 13.6, 0 , 0 , 1.5, 0 , q2
2000/03/13, 0.4, 0.9, 0 , 10.9, 1.7, 0.2, 4.4, 13.6, 0 , 0 , 1.5, q3
... , ..., ..., ..., ..., ..., ..., ..., ..., ..., ..., ..., ...
Case-2
| rrf0 | 当日の雨量 |
| rrf1 | 当日と前日の雨量の和 |
| rrf2 | 当日・前日・前々日の雨量の和 |
| ... | |
| rrf10 | 当日から10日前の雨量の和 |
入力データファイルのイメージ(Case-2)
date, rrf0, rrf1, rrf2, rrf3, rrf4, rrf5, rrf6, rrf7, rrf8, rrf9, rrf10, Qo
2000/03/01, 0.2
2000/03/02, 0 , 0.2
2000/03/03, 1.5, 1.5, 1.7
2000/03/04, 0 , 1.5, 1.5, 1.7
2000/03/05, 0 , 0 , 1.5, 1.5, 1.7
2000/03/06, 13.6, 13.6, 13.6, 15.1, 15.1, 15.3
2000/03/07, 4.4, 18 , 18 , 18 , 19.5, 19.5, 19.7
2000/03/08, 0.2, 4.6, 18.2, 18.2, 18.2, 19.7, 19.7, 19.9
2000/03/09, 1.7, 1.9, 6.3, 19.9, 19.9, 19.9, 21.4, 21.4, 21.6
2000/03/10, 10.9, 12.6, 12.8, 17.2, 30.8, 30.8, 30.8, 32.3, 32.3, 21.6
2000/03/11, 0 , 10.9, 12.6, 12.8, 17.2, 30.8, 30.8, 30.8, 32.3, 32.3, 32.5, q1
2000/03/12, 0.9, 0.9, 11.8, 13.5, 13.7, 18.1, 31.7, 31.7, 31.7, 32.3, 33.2, q2
2000/03/13, 0.4, 1.3, 1.3, 12.2, 13.9, 14.1, 18.5, 32.1, 32.1, 31.7, 33.6, q3
... , ..., ..., ..., ..., ..., ..., ..., ..., ..., ..., ..., ...
どっちがいいか?
今回用いた入力データでは、Case-2の方が相関が良かったので、以降はCase-2の入力データを用いることとする。
なお、何日前までの雨量を入力に取り入れるかは、サイトの条件にもよるため、場合場合により変える必要があるであろう。
出力事例
- 各手法のうち、Ridge, Lasso, SVR,MLP についてはグリッドサーチによるパラメータ最適化をいれてある。その他の手法についてはパラメータは固定としいる。
- データは17年分あるが、学習は初期の3年間(train_size=0.175)とし、残り14年はtestデータとしている。
- 時系列データではあるが、時系列の効果は入力データに反映されているものとし、trainデータはランダムにシャッフルしている。
MinMaxScalerによる前処理のみ
スケーリング処理のみの場合は、非線形を追跡できるSVR(カーネル:rbf)とニューラルネットワーク(MLP)でよい予測結果が得られている。
X_train.shape: (1086, 11)
y_train.shape: (1086, 1)
X_test.shape: (5123, 11)
y_test.shape: (5123, 1)
* LinearRegression
Training set score : 0.819
Test set score : 0.824
* Ridge
Best parameters: {'alpha': 0.1}
Best cross-validation score: 0.809
Test set score with best parameters: 0.824
* Lasso
Best parameters: {'alpha': 0.01, 'max_iter': 100000}
Best cross-validation score: 0.810
Test set score with best parameters: 0.824
* SVR(linear)
Best parameters: {'C': 10000.0, 'kernel': 'linear'}
Best cross-validation score: 0.787
Test set score with best parameters: 0.786
* SVR(rbf)
Best parameters: {'C': 10000.0, 'epsilon': 1.0, 'gamma': 0.1, 'kernel': 'rbf'}
Best cross-validation score: 0.891
Test set score with best parameters: 0.912
* MLP
Best parameters: {'activation': 'relu', 'alpha': 10, 'hidden_layer_sizes': (10, 10), 'solver': 'lbfgs'}
Best cross-validation score: 0.895
Test set score with best parameters: 0.905
* RandomForest
Training set score : 0.978
Test set score : 0.849
* GradientBoosting
Training set score : 0.963
Test set score : 0.850
* KNeighbors
Training set score : 0.898
Test set score : 0.835
MinMaxScalerによる前処理+多項式特徴量(2次)追加
2次の多項式特徴量を加えると、線形回帰でも、多項式特徴量を加えない場合と比べ、予測精度は上がっている。決定木およびK近傍法では予測精度の改善は見られない。
決定木およびk近傍法では、予測結果が頭打ちになっていることもわかる。これは、教師データをはじめの3年(2001・2002・2003年)としているが、テスト側では2008・2010・2012・2016・2017年など、明らかに年雨量がはじめの3年より大きい年があり、これらの年では教師データで経験していない雨量が多く存在していると考えられ、決定木およびk近傍法は外挿には対応できないことを示していると考えられる。
X_train.shape: (1086, 78)
y_train.shape: (1086, 1)
X_test.shape: (5123, 78)
y_test.shape: (5123, 1)
* LinearRegression
Training set score : 0.914
Test set score : 0.888
* Ridge
Best parameters: {'alpha': 0.1}
Best cross-validation score: 0.892
Test set score with best parameters: 0.905
* Lasso
Best parameters: {'alpha': 0.01, 'max_iter': 100000}
Best cross-validation score: 0.892
Test set score with best parameters: 0.905
* SVR(linear)
Best parameters: {'C': 1000.0, 'kernel': 'linear'}
Best cross-validation score: 0.892
Test set score with best parameters: 0.905
c:\users\tscadmin\appdata\local\programs\python\python37\lib\site-packages\sklearn\model_selection\_search.py:841: DeprecationWarning: The default of the `iid` parameter will change from True to False in version 0.22 and will be removed in 0.24. This will change numeric results when test-set sizes are unequal.
DeprecationWarning)
* SVR(rbf)
Best parameters: {'C': 10000.0, 'epsilon': 1.0, 'gamma': 0.01, 'kernel': 'rbf'}
Best cross-validation score: 0.885
Test set score with best parameters: 0.910
* MLP
Best parameters: {'activation': 'relu', 'alpha': 100, 'hidden_layer_sizes': (10, 10), 'solver': 'lbfgs'}
Best cross-validation score: 0.901
Test set score with best parameters: 0.911
* RandomForest
Training set score : 0.977
Test set score : 0.852
* GradientBoosting
Training set score : 0.968
Test set score : 0.858
* KNeighbors
Training set score : 0.892
Test set score : 0.827
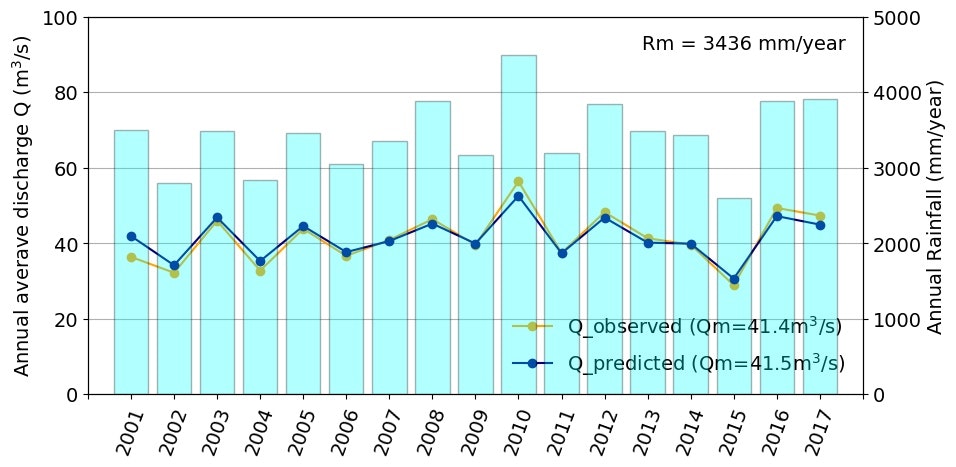
Lasso回帰(多項式特徴量追加)での流量予測結果
重回帰による流量予測プログラム
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
# global variables
fsz=12
xmin=0; ymin=0
xmax=600; ymax=600
bw=3; icol=3; irow=3
def drawfig(y_test, y_pred, ss, nplt):
#=======================
# i=1 i=2 i=3
# i=4 i=5 i=6
# i=7 i=8 i=9
#=======================
plt.subplot(irow, icol, nplt)
plt.gca().set_aspect('equal',adjustable='box')
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
if 7<=nplt:
plt.xlabel('y_test')
else:
plt.xticks([])
if nplt==1 or nplt==4 or nplt==7:
plt.ylabel('y_predicted')
else:
plt.yticks([])
plt.plot(y_test, y_pred, 'o')
plt.plot([xmin,xmax],[ymin,ymax],'-')
xs=xmin+0.05*(xmax-xmin)
ys=ymin+0.95*(ymax-ymin)
plt.text(xs, ys, ss, va='top', ha='left', fontsize=fsz)
def lin(X_train, X_test, y_train, y_test, XXd):
reg=LinearRegression()
reg.fit(X_train, y_train)
sc_tra=reg.score(X_train, y_train)
sc_tes=reg.score(X_test, y_test)
y_pred=reg.predict(X_test)
print('* LinearRegression')
print('{0:25s}: {1:.3f}'.format('Training set score',sc_tra))
print('{0:25s}: {1:.3f}'.format('Test set score',sc_tes))
ss='LinearReg\n'+'R$^2$={0:.3f}'.format(sc_tes)
nplt=1; drawfig(y_test, y_pred, ss, nplt)
yp_all=reg.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def rid(X_train, X_test, y_train, y_test, XXd):
alp = [0.0001, 0.001, 0.01, 0.1, 1, 10, 100]
param_grid={'alpha': alp}
grid=GridSearchCV(Ridge(), param_grid, cv=5)
grid.fit(X_train, y_train)
test_score=grid.score(X_test, y_test)
y_pred=grid.predict(X_test)
print('* Ridge')
print('Best parameters: {}'.format(grid.best_params_))
print('Best cross-validation score: {0:.3f}'.format(grid.best_score_))
print('Test set score with best parameters: {0:.3f}'.format(test_score))
ss = 'Ridge\n'
ss = ss +'R$^2$={0:.3f}'.format(test_score)
nplt=2; drawfig(y_test, y_pred, ss, nplt)
yp_all=grid.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def las(X_train, X_test, y_train, y_test, XXd):
alp = [0.0001, 0.001, 0.01, 0.1, 1, 10, 100]
param_grid={'alpha': alp, 'max_iter': [100000]}
grid=GridSearchCV(Lasso(), param_grid, cv=5)
grid.fit(X_train, y_train)
test_score=grid.score(X_test, y_test)
y_pred=grid.predict(X_test)
print('* Lasso')
print('Best parameters: {}'.format(grid.best_params_))
print('Best cross-validation score: {0:.3f}'.format(grid.best_score_))
print('Test set score with best parameters: {0:.3f}'.format(test_score))
ss = 'Lasso\n'.format(alp)
ss = ss +'R$^2$={0:.3f}'.format(test_score)
nplt=3; drawfig(y_test, y_pred, ss, nplt)
yp_all=grid.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def sv1(X_train, X_test, y_train, y_test, XXd):
cc=[1e0, 1e1, 1e2, 1e3, 1e4]
param_grid={'kernel': ['linear'], 'C': cc}
grid=GridSearchCV(SVR(), param_grid, cv=5)
grid.fit(X_train, y_train)
test_score=grid.score(X_test, y_test)
y_pred=grid.predict(X_test)
print('* SVR(linear)')
print('Best parameters: {}'.format(grid.best_params_))
print('Best cross-validation score: {0:.3f}'.format(grid.best_score_))
print('Test set score with best parameters: {0:.3f}'.format(test_score))
ss='SVR(linear)\n'+'R$^2$={0:.3f}'.format(test_score)
nplt=4; drawfig(y_test, y_pred, ss, nplt)
yp_all=grid.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def sv2(X_train, X_test, y_train, y_test, XXd):
cc=[1e0, 1e1, 1e2, 1e3, 1e4]
gg=[1e-4, 1e-3, 1e-2, 1e-1, 1e0, 1e1]
param_grid={'kernel': ['rbf'], 'C': cc, 'gamma': gg, 'epsilon': [1.0]}
grid=GridSearchCV(SVR(), param_grid, cv=5)
grid.fit(X_train, y_train)
test_score=grid.score(X_test, y_test)
y_pred=grid.predict(X_test)
print('* SVR(rbf)')
print('Best parameters: {}'.format(grid.best_params_))
print('Best cross-validation score: {0:.3f}'.format(grid.best_score_))
print('Test set score with best parameters: {0:.3f}'.format(test_score))
ss='SVR(rbf)\n'+'R$^2$={0:.3f}'.format(test_score)
nplt=5; drawfig(y_test, y_pred, ss, nplt)
yp_all=grid.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def mlp(X_train, X_test, y_train, y_test, XXd):
alp=[1e-4, 1e-3, 1e-2, 1e-1, 1e0, 10, 100]
param_grid={'solver': ['lbfgs'], 'activation': ['relu'], 'hidden_layer_sizes': [(100,),(10,10)], 'alpha': alp}
grid=GridSearchCV(MLPRegressor(), param_grid, cv=5)
grid.fit(X_train, y_train)
test_score=grid.score(X_test, y_test)
y_pred=grid.predict(X_test)
print('* MLP')
print('Best parameters: {}'.format(grid.best_params_))
print('Best cross-validation score: {0:.3f}'.format(grid.best_score_))
print('Test set score with best parameters: {0:.3f}'.format(test_score))
ss='MLP\n'+'R$^2$={0:.3f}'.format(test_score)
nplt=6; drawfig(y_test, y_pred, ss, nplt)
yp_all=grid.predict(XXd)
return yp_all
def rfr(X_train, X_test, y_train, y_test, XXd):
reg=RandomForestRegressor(n_estimators=1000)
reg.fit(X_train, y_train)
sc_tra=reg.score(X_train, y_train)
sc_tes=reg.score(X_test, y_test)
y_pred=reg.predict(X_test)
print('* RandomForest')
print('{0:25s}: {1:.3f}'.format('Training set score',sc_tra))
print('{0:25s}: {1:.3f}'.format('Test set score',sc_tes))
ss='RandomForest\n'+'R$^2$={0:.3f}'.format(sc_tes)
nplt=7; drawfig(y_test, y_pred, ss, nplt)
yp_all=reg.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def gbr(X_train, X_test, y_train, y_test, XXd):
reg=GradientBoostingRegressor(n_estimators=100, max_depth=3, random_state=0)
reg.fit(X_train, y_train)
sc_tra=reg.score(X_train, y_train)
sc_tes=reg.score(X_test, y_test)
y_pred=reg.predict(X_test)
print('* GradientBoosting')
print('{0:25s}: {1:.3f}'.format('Training set score',sc_tra))
print('{0:25s}: {1:.3f}'.format('Test set score',sc_tes))
ss='GradientBoosting\n'+'R$^2$={0:.3f}'.format(sc_tes)
nplt=8; drawfig(y_test, y_pred, ss, nplt)
yp_all=reg.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def knb(X_train, X_test, y_train, y_test, XXd):
reg=KNeighborsRegressor(n_neighbors=5)
reg.fit(X_train, y_train)
sc_tra=reg.score(X_train, y_train)
sc_tes=reg.score(X_test, y_test)
y_pred=reg.predict(X_test)
print('* KNeighbors')
print('{0:25s}: {1:.3f}'.format('Training set score',sc_tra))
print('{0:25s}: {1:.3f}'.format('Test set score',sc_tes))
ss='KNeighbors\n'+'R$^2$={0:.3f}'.format(sc_tes)
nplt=9; drawfig(y_test, y_pred, ss, nplt)
yp_all=reg.predict(XXd)
yp_all = np.reshape(yp_all, (-1, ))
return yp_all
def inp_rf():
# input rainfall data
#fnameR='data_reg.csv'
fnameR='data_reg_1.csv'
df = pd.read_csv(fnameR, header=0, index_col=0)
df.index = pd.to_datetime(df.index, format='%Y-%m-%d')
df=df[df.index >= '2001-01-01'] # data after 2001-01-01 is available
df=df[df.index <= '2017-12-31'] # data before 2017-12-31 is available
return df
def main():
df0 = inp_rf() # input data
#XX=df0.loc[:,['rf0','rf1','rf2','rf3','rf4','rf5','rf6','rf7','rf8','rf9','rf10',
# 'rf11','rf12','rf13','rf14','rf15','rf16','rf17','rf18','rf19','rf20']]
#XX=df0.loc[:,['rf0','rf1','rf2','rf3','rf4','rf5','rf6','rf7','rf8','rf9','rf10']]
XX=df0.loc[:,['rrf0','rrf1','rrf2','rrf3','rrf4','rrf5','rrf6','rrf7','rrf8','rrf9','rrf10']]
yy=df0.loc[:,['Qo']]
for iii in [2,3]:
X_train, X_test, y_train, y_test = train_test_split(
XX, yy, train_size=0.175, random_state=0)
#X_train, X_test, y_train, y_test = train_test_split(
# XX, yy, train_size=0.176, shuffle=False, stratify=None)
if iii==1:
pass
if iii==2:
pipe=Pipeline([
('scaler', MinMaxScaler())
])
if iii==3:
pipe=Pipeline([
('scaler', MinMaxScaler()),
('poly', PolynomialFeatures(degree=2,include_bias=False))
])
pipe.fit(X_train, y_train)
X_train=pipe.transform(X_train)
X_test=pipe.transform(X_test)
XXd=pipe.transform(XX)
print('X_train.shape: {}'.format(X_train.shape))
print('y_train.shape: {}'.format(y_train.shape))
print('X_test.shape: {}'.format(X_test.shape))
print('y_test.shape: {}'.format(y_test.shape))
plt.figure(figsize=(bw*icol,bw*irow), facecolor='w')
plt.subplots_adjust(wspace=0.1, hspace=0.1)
yp1 = lin(X_train, X_test, y_train, y_test, XXd)
yp2 = rid(X_train, X_test, y_train, y_test, XXd)
yp3 = las(X_train, X_test, y_train, y_test, XXd)
yp4 = sv1(X_train, X_test, y_train, y_test, XXd)
yp5 = sv2(X_train, X_test, y_train, y_test, XXd)
yp6 = mlp(X_train, X_test, y_train, y_test, XXd)
yp7 = rfr(X_train, X_test, y_train, y_test, XXd)
yp8 = gbr(X_train, X_test, y_train, y_test, XXd)
yp9 = knb(X_train, X_test, y_train, y_test, XXd)
print(yp1.shape)
print(yp2.shape)
print(yp3.shape)
print(yp4.shape)
print(yp5.shape)
print(yp6.shape)
print(yp7.shape)
print(yp8.shape)
print(yp9.shape)
#plt.tight_layout()
fnameF='fig_reg_rf_10-'+str(iii)+'.jpg'
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
dfx = pd.DataFrame({'date' : df0.index.values,
'Rf' : df0['rf0'],
'Qo' : df0['Qo'],
'lin' : yp1,
'rid' : yp2,
'las' : yp3,
'sv1' : yp4,
'sv2' : yp5,
'mlp' : yp6,
'rfr' : yp7,
'gbr' : yp8,
'knb' : yp9
})
dfx = dfx.set_index('date')
if iii==2: dfx.to_csv('df2.csv')
if iii==3: dfx.to_csv('df3.csv')
# ==============
# Execution
# ==============
if __name__ == '__main__': main()
流量予測結果のグラフのプログラムはこれと同じなので省略。
以 上