- はじめに
=========
本記事では、姿勢制御モジュール(mc_att_control)の解説に引き続き、PX4/Firmwareのマルチコプター位置制御モジュール(mc_pos_control)に実装されているアルゴリズムをコードベースで解説しています。以下の予備知識があると理解が捗ると思います。
- PID制御
- ブロック線図
本記事は次のような方に適しています。
- ドローン(マルチコプター)の飛行制御の概要を知りたい
- ソースコードの基本動作を理解するための参考にしたい
対象ソースコード
Tag: 1.6.0 Release RC1
- 全体像
=========
制御アルゴリズムはvoid MulticopterPositionControl::control_position(float dt)に記述されています。ただし、このコードは内部のモードや飛行の状態によって動作が異なるため、すべてを一度に説明すると理解しにくくなります。そこで本記事では、ホバリング状態を仮定して簡略化した制御アルゴリズムの動作について説明することとします。
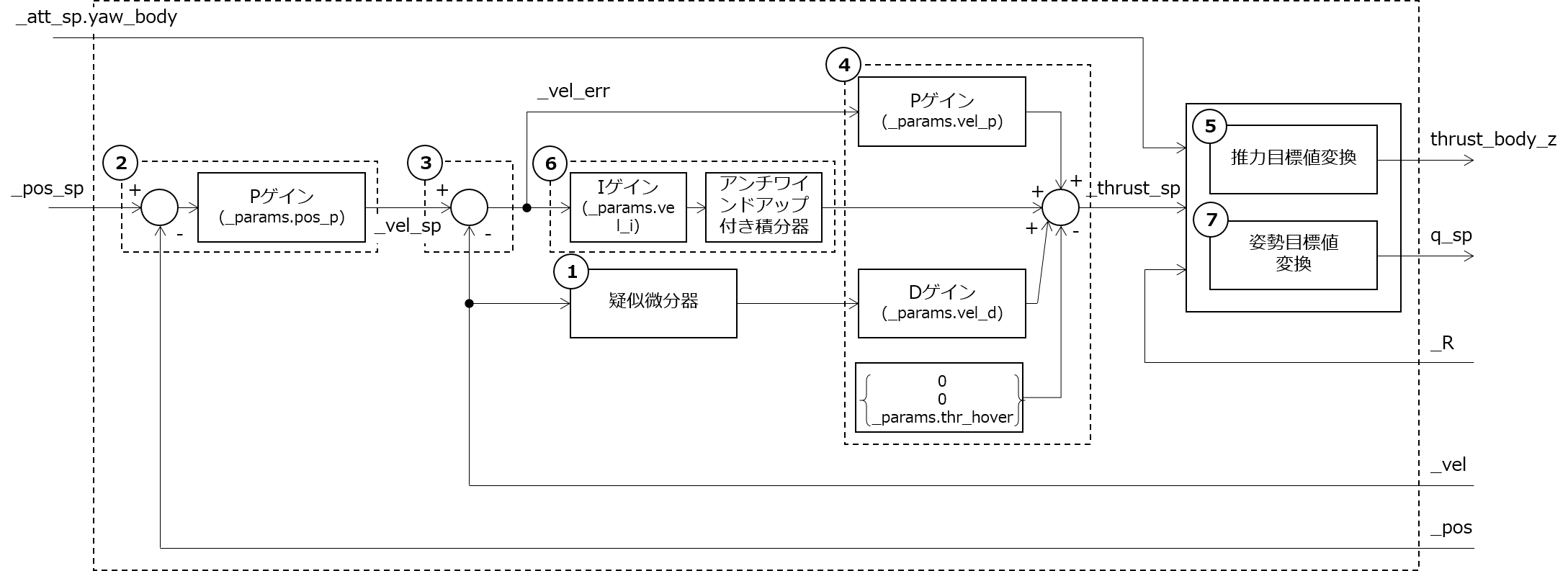
このときの制御器をブロック図で表すと次のようになります。
制御器には制御ループが2つあり、外側にP制御による位置の制御ループ、内側にPID制御による速度の制御ループがあります。また、位置や速度はNED座標系(NED:North-East-Down)で定義され、0番目の要素がX軸(北方向)、1番目の要素がY軸(東方向)、2番目の要素がZ方向(重力方向)となっています。
今回はホバリング状態を仮定していますが、ウェイポイント間の移動を考えると飽和要素の働きに対する理解が必要となります。この解説はいずれ詳細版でしようと思います。
-
位置-速度制御の動作
==========
処理の流れは次のようになっています。2番から順番に該当するコードを紹介していきたいと思います。 -
速度の疑似微分の計算
-
速度目標値の計算(位置制御)
-
速度偏差の計算
-
目標推力ベクトルの計算(速度制御)
-
目標推力の計算
-
積分値の更新
-
目標姿勢の計算
速度目標値の計算(位置制御)
位置の制御演算部分を抜き出すと次のようになります。位置目標値_pos_spと現在位置_posの差に対してPゲイン_params.pos_pをかけ、速度目標値として_vel_spに格納しています。
_vel_sp(0) = (_pos_sp(0) - _pos(0)) * _params.pos_p(0);
_vel_sp(1) = (_pos_sp(1) - _pos(1)) * _params.pos_p(1);
_vel_sp(2) = (_pos_sp(2) - _pos(2)) * _params.pos_p(2);
速度偏差の計算
速度偏差vel_errは単純に、速度目標値と現在速度_velの差となります。
/* velocity error */
math::Vector<3> vel_err = _vel_sp - _vel;
目標推力ベクトルの計算(速度制御)
PID制御により、目標推力ベクトルthrust_spを求めます。先頭から、比例成分、微分成分、積分成分、定数成分の和となっています。定数成分は重力との釣り合い成分に相当します。
thrust_sp = vel_err.emult(_params.vel_p) + _vel_err_d.emult(_params.vel_d)
+ _thrust_int - math::Vector<3>(0.0f, 0.0f, _params.thr_hover);
微分成分は偏差ではなく速度にのみゲインが作用する構成となっており、姿勢制御と同様に微分先行型PID制御を行っています。(_vel_err_dの更新は速度成分のみで行われています。参照:_vel_err_dの更新処理)
微分要素は疑似微分と呼ばれる方式を使っています。通常の微分にはノイズを増幅する性質があり、これが問題になることがありますが、疑似微分にはローパスフィルタでノイズの高周波成分をカットする性質があるため、微分が持つノイズ増幅の影響を抑えることができます。
推力目標値変換
ここでは、目標推力ベクトルから機体に垂直な成分を取り出す処理を行っています。R_zは、現在の機体下方向を表す単位ベクトルです。ここでの処理で求まったthrust_body_zは、最終的に機体垂直軸に対する運動を制御する制御入力となります。
matrix::Vector3f R_z(_R(0, 2), _R(1, 2), _R(2, 2));
matrix::Vector3f F(thrust_sp.data);
float thrust_body_z = F.dot(-R_z); /* recalculate because it might have changed */
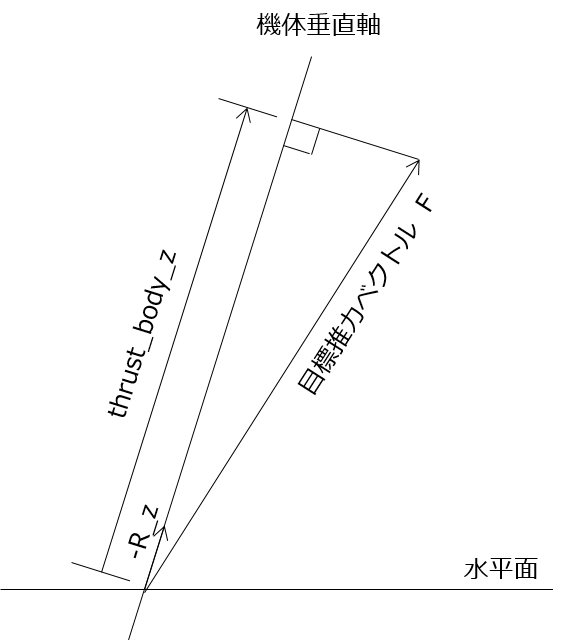
F.dot(-R_z)は、Fと-R_zの内積を意味します。変数同士の関係を図にすると次のようになります。
積分値の更新
積分値の更新部分を抜き出すと次のとおりとなります。実際はアンチワインドアップの処理も実装されていますが、ホバリング状態では基本的に作動しないため省略しています。
_thrust_int(0) += vel_err(0) * _params.vel_i(0) * dt;
_thrust_int(1) += vel_err(1) * _params.vel_i(1) * dt;
_thrust_int(2) += vel_err(2) * _params.vel_i(2) * dt;
目標姿勢の計算
この部分では、目標推力ベクトルの方向に機体を傾斜させるために必要な姿勢を計算します。マルチコプターの推力は必ず機体の上方向に生じると仮定すると、機体のZ軸を目標推力ベクトルの逆方向に定めることができます。残りのX軸とY軸は、別途与えられている目標方位から算出されます。
処理は自体は、大きく分けて次の2つの処理から構成されています。
- 目標推力ベクトルの方向と目標方位から、機体のX軸、Y軸、Z軸方向を求める。
- 機体のX軸、Y軸、Z軸方向をクォータニオンに変換し、姿勢目標値とする。
以下のコードが1に該当するコードとなります。イレギュラーに対応するコードはホバリング状態では基本的に実行されないため省略しています。
/* desired body_z axis = -normalize(thrust_vector) */
math::Vector<3> body_x;
math::Vector<3> body_y;
math::Vector<3> body_z;
body_z = -thrust_sp.normalized();
/* vector of desired yaw direction in XY plane, rotated by PI/2 */
math::Vector<3> y_C(-sinf(_att_sp.yaw_body), cosf(_att_sp.yaw_body), 0.0f);
/* desired body_x axis, orthogonal to body_z */
body_x = y_C % body_z;
/* keep nose to front while inverted upside down */
if (body_z(2) < 0.0f) {
body_x = -body_x;
}
body_x.normalize();
/* desired body_y axis */
body_y = body_z % body_x;
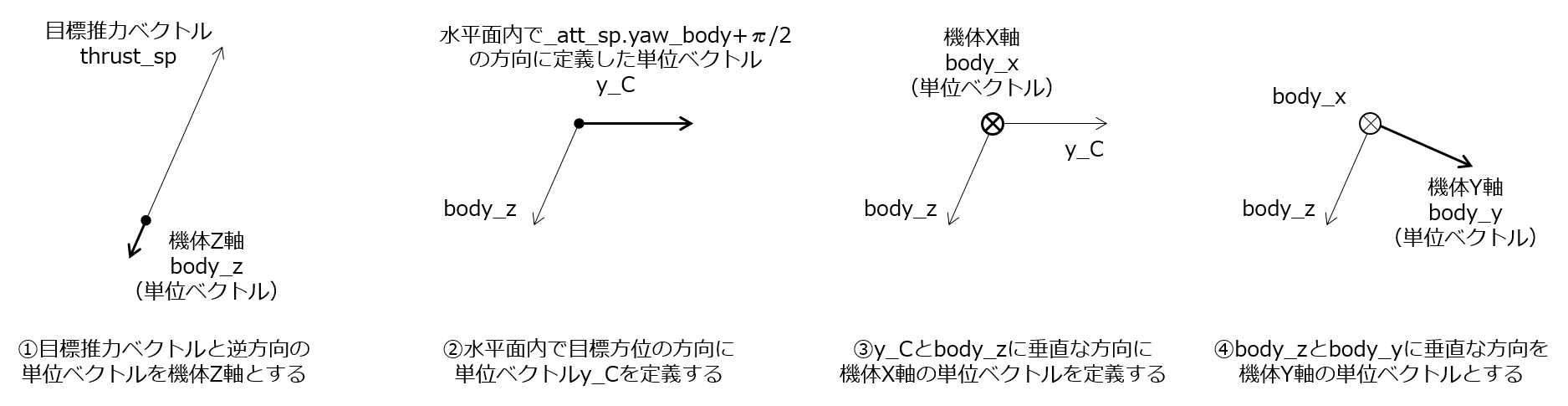
この内容を図で表すとこのようになります。
最後に以下のコードが2のクォータニオン化に該当する部分となります。機体姿勢を表すX軸、Y軸、Z軸から回転行列を作り、matrix::Quatfのインスタンス生成時にクォータニオンへ変換しています。
/* fill rotation matrix */
for (int i = 0; i < 3; i++) {
_R_setpoint(i, 0) = body_x(i);
_R_setpoint(i, 1) = body_y(i);
_R_setpoint(i, 2) = body_z(i);
}
/* copy quaternion setpoint to attitude setpoint topic */
matrix::Quatf q_sp = _R_setpoint;
ここで求まった目標姿勢は下位の姿勢制御器に渡され、実姿勢が目標姿勢に一致するよう制御が行われます。
- おわりに
=========
PX4の姿勢制御の解説に引き続き、位置制御の解説を行いました。姿勢制御とともに推力ベクトルをうまく取り扱うことで、線形制御でありながら大姿勢に対応できる制御を行っているようです。簡略化のために説明を省略した部分にもドローンの挙動を細かく知るために重要な処理があるので、別記事にて解説しようと思います。(需要あるかな?)