Intro
今更BK-Treeを紹介します。
BK-Treeは類似度を表すメトリックに基づいて、
range search(あるクエリから閾値以下の値を持つノードを列挙すること)を行うためのデータ構造です。
線形に探索するより速く、spell checkや曖昧検索などによく使われます。
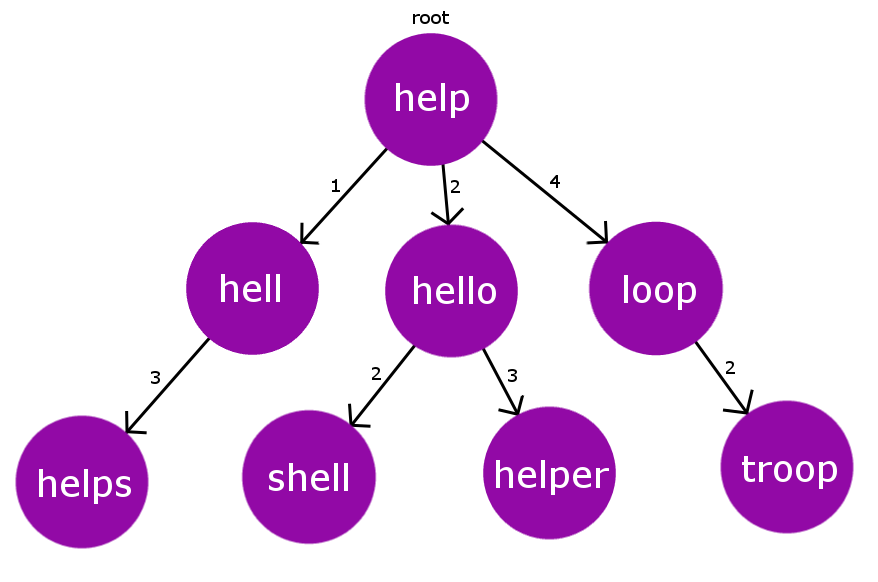
例えば辞書からある単語に似ている単語を列挙したいなら、辞書から以下のような木を構築します。
記事のモチベーション
なぜBK-treeの枝刈りがうまくいくのか、
詳しく書いてある記事があまりなかったためです。
「そんなことわかるでしょ」って感じの記事が多かった・・・。
原著
元はファイルの曖昧検索ための論文Some Approaches to Best-Match File Searchingで導入されました。
著者のW.A. BurkhardとR.M. Kellerの頭文字をとって、BK-Treeと呼ばれています。
利用可能なメトリック
厳密なメトリックの定義を満たす必要はありませんが、
以下の条件を満たす必要があります。
- 三角不等式を満たす
- 基本的には離散値をとる
そのため文字列が対象のデータ集合なら、レーベンシュタイン距離などの編集距離が用いられることが多いです。
構築方法
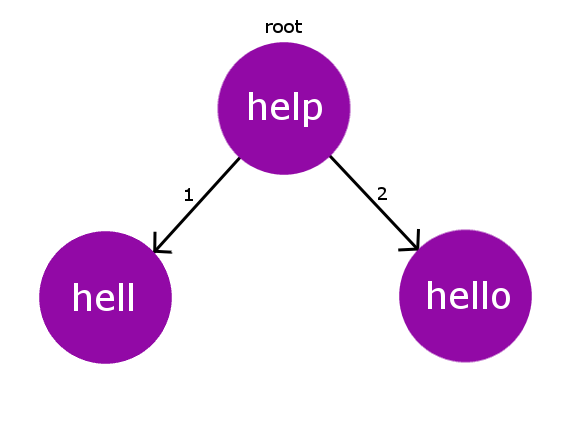
- 最初にrootとなる文字列を選びます。
- rootとなる文字列rと辞書の中から選んだ文字列cのメトリック$d=D(r, c)$を計算します。
dがかぶらないように、rootに子node(図ではhellとhello)を追加します。左から小さいdが並ぶように挿入します。
つまり子nodeは互いに違うdを持っています。
これを全ての単語に対して繰り返します。
dが衝突してしまった場合は同じdを持つ子ノードc'の子ノードにします。 (図ではshell)
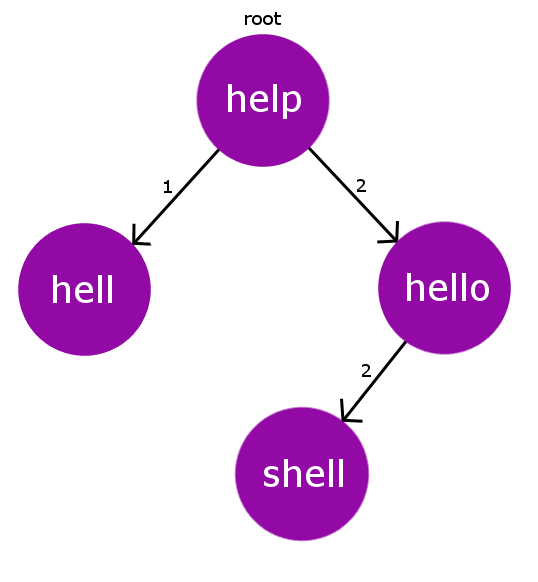
このとき、c'の文字列と$d'=D(c', c)$をrootの場合と同様に元にd'がc'の子ノードの中で衝突しないように左から昇順に挿入いたします。
もしこれも衝突してしまった場合は、挿入場所が見つかるまで再帰的に繰り返します。
探索方法
構築済みの木に対して、以下のように探索を行います。
- ルートノードrとクエリーxとのメトリック$D(r, x)$を計算します。
$D(r, x) <= t$ なら候補に加えます。 - 次に子ノードcと比較をします。
すべての子ノードを見ていては、総当たりと変わりがないので、枝刈りを行います。
そこで、
$$D(r, x) - t < D(r, c) < D(r, x) + t \tag{1}$$
となるcだけを探索対象とします。
なお、性能はここでどれだけ枝刈りの対象になるかで決まります。
3. これを末端になるまで繰り返します。
簡易的な証明
なぜ式1で枝刈りをしていいのか以下に説明します。厳密な証明ではありません。
子ノードの場合
枝刈りしたノードcには、$$D(c, x) <= t$$ となるものが
ないのでしょうか?
枝刈りしたノードcは(1)とは逆に
$$D(r, x) + t <= D(r, c) \tag{2}$$
か
$$D(r, x) - t >= D(r, c) \tag{3}$$
が成り立ちます。
ノードr, cとクエリーxについて三角不等式
$$D(r, x) + D(c, x) > D(r, c) \tag{5}$$
$$D(r, c) + D(c, x) > D(r, x) \tag{6}$$
が成り立つので、
式(2)と式(5)、または式(3)と式(6)より
$$D(c, x) > t \tag{7}$$
が導けます。
よって(1)によって枝刈りされたノードcとクエリxのメトリックはすべてtより大きくなります。
孫ノードの場合
枝刈りした子ノードの下の孫ノードgにももしからしたら、$D(x, g) <= t$となるものが含まれるんじゃないと思うかもしれません。
(そんなわけないだろうって人は飛ばしてください。)
(余談ですが、この記事を書いた理由として自分はこの点がすぐにピンとこなかったためです。)
BK-treeの構造から、
孫ノードと子ノードはルートノードに対して同じ距離を持ちますので、
$$ D(r, c) = D(r, g) \tag{8}$$
三角不等式よりノードr, gとクエリxには
$$ D(r, g) + D(g, x) > D(r, x) \tag{9}$$
$$ D(r, x) + D(g, x) > D(r, g) \tag{10}$$
が成り立ちます。
式(3)(8)(9)または式(2)(8)(10)より
$$ t < D(g, x) \tag{11}$$
となり、やはり枝刈りされた子ノードの下のノードには
クエリーとのメトリックがt以下のノードは含まれていないことが分かります。
帰納的に孫より深いノードにもt以下の含まれていることはありません。
結び
実装についてはすでに多くのものがありますので、改めては紹介いたしません。
indexの圧縮を考えなければ、簡単に実装できますのでお試しください。
実はすでに同じ目的のアルゴリズムとして、
[SymSpellをすでに紹介いたしました。BK-Treeの性能比較の引用もそちらに乗っています。]
(https://qiita.com/daimonji-bucket/items/1f40bc3242a3d26133d0)
余談・疑問点
VP trees: A data structure for finding stuff fast
にVantage Point treeの一般化だと書かれているのですが、
具体的にどう一般化すればそうなるのか記述されているものが見つかりませんでした・・・。
VP-treeと差異を埋めるには、
- 離散値も許可する
- 子ノードを2つだけにする
- 一部backtrack探索を許可する
ことが必要ですが・・・