簡単に高速なスペルチェックや補完が実装できる?!symspellの紹介

Introduction

スペルチェックや補完、文字のあいまい検索が機能に欲しいってことってありますよね。

現在高性能なものは統計的学習ベース（特に日本語の場合かな漢字変換もあるので）と予測され、高性能です。
しかし大量のデータがなければ作成できません。

また代わりにElasticsearchやsolr、もしくはluceneを使う手もあります。
しかしその時間やリソースがない場面もあるかと思います。
(例えば、kaggleでもスペルチェックが有効な場面がありました。）

そこで辞書さえあれば実装できるアルゴリズムの一つを紹介いたします。
実装しやすく速いのでありがたいです。

オリジナル実装はWolf Garbeによるもので、こちらにあります。
wolfgarbe/SymSpell

オリジナルはC#ですがJavaやC++等の再実装が揃っています。

文字列の差異数ベースの手法

曖昧な文字列検索を簡単に実装するための代表的なアプローチには、
文字列を比較したときの差異数を指標とするものがあります。

それらには以下のような手法があります。1, 2は編集距離をもとにしています。
編集距離はここではlevenshtein距離またはその派生（Damerau-levenshtein, restricted Damerau-levenshteinなど）を指します。
levenshtein距離は、クエリーの単語を削除・挿入・置換（Damerau-levenshteinの場合は加えて転置）の操作を行って、
検索対象の単語に一致させるまでに必要な最小の回数を距離とします。

なおここでは検索対象の単語の集合を辞書、似たものを探したい単語をクエリーと読んでいます。　

1. LinSpell (編集距離を使った線形探索)
   すべての辞書の中にある単語と距離を計算し、閾値以下の候補のものが必要な数見つかり次第打ち切ります。
   インデックスを用いないため、事前計算は必要ありません。

2. BK-Tree レーベンシュタイン距離などの距離（厳密ではなく三角不等式が成立する指標）に基づいて、 辞書の単語をノードとした木構造を構築します。 三角不等式を利用して、枝狩りを行いながら末端の葉まで候補の単語を上げていきます。 図が無いと説明してもわかりにくいので、 [この解説](https://www.geeksforgeeks.org/bk-tree-introduction-implementation/)等をごらんください。
3. [Norvig's algorithm](http://www.norvig.com/spell-correct.html) 辞書の単語に文字の削除・挿入・置換・転置・分割を決められた回数行い、文字列を生成します。 これらの文字列をインデックスとして利用します。 置換と挿入は文字のバリエーションの分だけ候補を生成します。 （つまりアルファベットだけなら、1文字あたり26種類（置換の場合25種類))

利点として事前にあらかじめ計算することができ、 同じ辞書に対しては何回検索しても高速です。 
検索エンジンのインデックスとして用いることができます。  
他の特徴量を加えて、優先度の高いものが先にでるように拡張することもできます  

これらの手法の問題点

1. 探索時に遅い
   LinSpellとBK-Treeは辞書が大きいと探索時に遅いことがあります。
   編集距離の計算回数が多いためです。
   一般的なdynamic programmingを用いたレーベンシュタイン距離のtime complexityは$O(n)$（nは文字列の長さ、同じ長さの文字列と仮定）、
   もっとも速いアルゴリズム(Masek and Paterson, 1980)でも$O(n^2/ log_2{n})$です。
   （実はLinSpellの場合編集距離の閾値kより大きな編集距離を正確に求める必要がなければ、途中で計算を打ち切れます。
   そのため、こちらのautomaton実装のように$O(k)$ですみます。）
   辞書の単語がN個だとするとLinSpellなら、けっして軽くないこれらの処理をN回計算しなければなりません。

   一方BK-Treeだと事前計算をしておくことでかなり範囲を絞れます。絞れる範囲は完全に辞書とクエリーに依存します。
   そのため本来はデータごとに実測するしかないのですが、どうも絞った後もかなりの比較が必要になるようです。
   例えばこのblogの実験では、閾値が4だと辞書の単語の17%~61%の計算が必要だったようです。

2. 構築時に遅い これはNorvig's algorithmの問題です。 生成するindexのバリエーションが多いため、構築時に時間がかかることがあります。 特に置換や挿入は日本語/中国語等だと膨大な数になります。漢字など文字の種類が多いためです。中国語なら 70,000種類もあります。 これらの言語ではそもそも実用的ではありません。
3. メモリ使用量が大きい 2.と同じ原因でおこる、Norvig's algorithmの問題です。

SymSpellのアルゴリズム

SymSpellは前述の方法より少ないindexのバリエーションで、高速な探索を実現しています。
もともとはこちらなどで紹介されています。
1000x Faster Spelling Correction algorithm | FAROO Blog

インデックスの構築

辞書の単語から0文字～k文字削除した転置インデックスを作成します。
kは何文字違いまで許容するかの閾値です。
例えばk=2とすると"ドラえもん"という単語から、

• [ドラえもん]
• [ラえもん, ドえもん, ドラもん, ドラえん, ドラえも]
• [えもん, ラもん, ラえん, ラえも,
  ドもん, ドえん, ドえも,
  ドラん, ドラも,
  ドラえ]　　

というインデックスが作られます。
当然違う単語から同じインデックスの項目が作られることもあります。
例えばk=2なら"ごえもん"からは"ドラえもん"と同じ"えもん"という項目が作成されます。
その場合は両方を候補として保持します。

探索

探索時にはクエリーの派生とindexの比較をすることになります

1. クエリーの単語とインデックスが一致している辞書の単語を取得します。
   もし見つからなければ、クエリーの単語から１文字削除した文字列を次のクエリーとして使います。
   これをサジェストの候補に必要な数が見つかるか、元のクエリーからk文字の削除が行われるまで繰り返します。
   例えば、"ハナえもん"という単語で先ほどのドラえもんが入った辞書を検索します。
   ２文字まで違いを許容すると、
   • "ハナえもん"で検索
     見つからず
   • "ナえもん", "ハえもん", "ハナもん", "ハナえん", "ハナえも"で検索
     見つからず
   • "えもん", "ナもん", "ナえん", "ナえも",
     "ハもん", "ハえん", "ハえも",
     "ハナん", "ハナも",
     "ハナえ",で検索
     "えもん"でヒット。ドラえもんを候補として加える。
     ２文字までしか違いを許容しないので、ここで検索を打ち切ります。
     候補として、[ドラえもん]を返します。

2. 元のクエリーの単語と候補の単語の編集距離を再計算し、閾値を超えた候補は外します。 厳密な編集距離でフィルターしたい場合、後述するように実際の編集距離との差異が発生する場合があるので再計算します。

prefix

長い文字列は生成されるindexが膨大な量になります。
そこでprefix、つまりは前から指定文字数だけをindexを作成するときと
クエリーとindexを比較するときに使います。
ただしprefixの長さが小さくなるとprecisionが下がるので、トレードオフになります。

なぜ範囲の絞り込みがうまくいくのか

このindexによる探索と絞り込みは、一見編集距離の概念からdeletionという点以外離れており、
recallかprecisionが下がるのではと思うかもしれません。
実は編集距離の概念と対応付けられます。

1. 削除はクエリーの単語から1文字削除することと同じ
   例
   • 辞書: ニャ クエリー: ニャー
   • 1文字削除済みのindex: ニャ

2. 挿入は辞書の単語から1文字削除することと同じ 例 - 辞書: 梅干し クエリー: 梅干 - 1文字削除済みのindex: 梅干
3. 置換は同じ位置の文字を辞書の単語とクエリーの単語からそれぞれ一文字ずつ削除したものが該当 例 - 辞書: オリンピック　クエリー: ゴリンピック - 1文字削除済みのindex: リンピック 1文字削除済みのクエリー: リンピック
4. 転置は辞書の単語と挿入から一文字ずつ削除したものが該当

• 例1
  - 辞書:　オリンピック　 　クエリー: オンリピック
  - 1文字削除済みのindex: オリピック 　1文字削除済みのクエリー: オリピック
• 例2
  • 辞書: ドグラ・マグラ 　　クエリー: ドマラ・ググラ
  • 2文字削除済みのindex: ドラ・グラ　　2文字削除済みのクエリー: ドラ・グラ

ただし、3,4は要注意です。実際の編集距離と差異がでることがあるためです。
例
- 辞書: パンク クエリー: ルパン
- 1文字削除済みのインデックス: パン　　1文字削除済みのクエリー: パン

しかしこれはrestricted Damerau-levenshtein距離やlevenshtein距離では2と計算されます。
そのため先ほど述べたように、候補を見つけた後に改めて編集距離を計算してフィルターする必要があります。

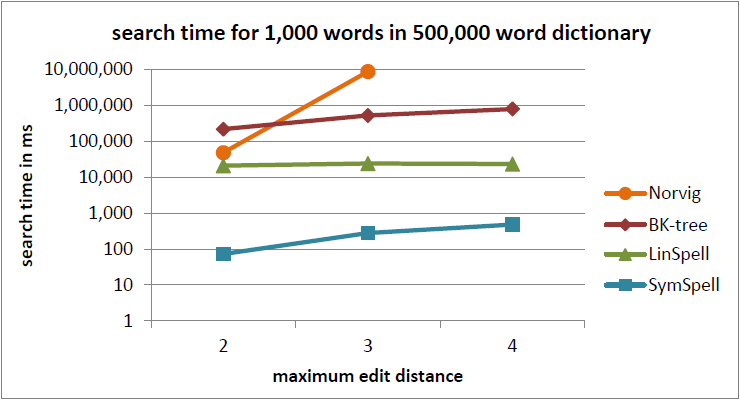
どれぐらい高速か

wolfgarbeのgithubページに掲載されているベンチマークを引用します。

100x速いというのもあながち嘘ではなさそうです。
ただし、このパフォーマンスベンチマークは以下の点が含まれていません。

• indexの構築時間の比較
• automaton（閾値打ち切り）実装のLinSpellとの比較
• テキストの長さを変えた場合の比較

これらの条件を含むベンチマークそのうちあらためて行いたいですね。

なぜ高速か

探索時

• 構築済みindex(通常はハッシュテーブルやfstなど)へのアクセスにより絞り込みはO(1)で済みます。
• 候補を閾値以下で絞り込んだ状態で行うので、該当しているものは少なく若干回数の編集距離の計算で済みます。

構築時

• 削除だけを行うので、一つの辞書の単語あたりから作られるindexのバリエーションが少なくて済みます

欠点

LinSpellやBK-treeに比べて、単純なメモリ消費量や事前計算が増えます。
指定された距離dの分だけ辞書の単語からバリエーションを生成するということは、
一単語当たり ${}_n \mathrm{C} _d$の記憶領域と事前計算が必要になります。　
(もちろんfstやdouble arrayでindexの圧縮は可能ですが・・・）

さらに長いtextはindexの生成に時間がかかります。　　
例えば20文字のtextから閾値3のindexを作ると1140種類ものバリエーションが生成されます。

プラグインとして実装してみました

OpenRefineのrecord linkageのpluginとして実装してみました。実用性はあまりなさそうですが・・・。