LoginSignup
2
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@dai08srhg

BoTorchで制約条件がブラックボックス関数の場合(Objective, Constrainsの利用)

Posted at

BoTorchでの制約条件の種類

BoTorchでは制約条件の種類と実装方法がいくつかあります．

パラメータに関する制約条件の場合

  • 特定次元の値の固定
  • パラメータに関する不等式制約，等式制約
    • 制約条件式が線形和の形で定義可能な場合
      • optimize_acqf()のinequality_constraints, equality_constraintsオプションで指定
    • 非線形の制約条件式の場合
      • optimize_acqf()のnonlinear_inequality_constraintsオプションで指定

制約条件もブラックボックス関数の場合

  • 本記事で扱います

制約条件もブラックボックス関数の場合

パラメータに関する制約条件であれば, 探索空間を限定することで明示的に制約条件を適用することができますが, 制約条件もブラックボックス関数の場合が存在します.

タスク例
$y_1$の合格基準は10以下であるため， $y_1 < 10$ を満たす領域で $y_2$ を最大化したい

※ただし, $y_1, y_2$は観測して初めて正確な観測値が得られる

ブラックボックス制約を扱うアプローチはいくつか提案されていますが, BoTorchで採用されているのはその中でも最もポピュラーな手法の1つである, 獲得関数の評価値に「制約条件を満たす確率」を掛け合わせる手法です.

[J.R. Gardner, et al., 2014],
[B. Letham, et al., 2019]

簡単のために, 以下のような制約関数が1つの場合を例に考えます.

\max f(\boldsymbol{x})\quad {\rm s.t.}\,\,c(\boldsymbol{x}) \le 0

※ 式を整理すれば， 大体の制約条件は $c(\boldsymbol{x}) \le 0$ の形に帰着可能です.

$f, c$それぞれを独立したガウス過程に従うと過程します.

f \sim \mathcal{GP}(0, k), \quad c \sim\mathcal{GP}(0, k_c)

例として, 獲得関数にExpected Improvement ($\rm EI$)　を利用する場合を考えると, 獲得関数 $\alpha_{\rm EI}(\boldsymbol{x})$は以下のように定義されます.

\alpha_{{\rm EI}} (\boldsymbol{x}) = \mathbb{E}[\max(0, f - f_{\rm best})]

これに対し, 制約付き${\rm EI}$は, 制約を満たす確率$\Delta(\boldsymbol{x})$を考えて以下のように定義されます.

\alpha_{{\rm CEI}} (\boldsymbol{x}) = \mathbb{E}[\Delta(\boldsymbol{x}) \max(0, f - f_{\rm best})]

$\Delta(\boldsymbol{x})$のモデリング方法としてはいくつか考えられます.
例えば, $\Delta(\boldsymbol{x})$を以下のパラメータで定まるベルヌーイ分布に従う確率変数とします.

p = P(c \le 0 | \boldsymbol{x}, \mathcal{D}_n) = \int_{-\infty}^{0}p(c | \boldsymbol{x}, \mathcal{D})dc

ここで, $p(c | \boldsymbol{x}, \mathcal{D})$はガウス過程としてモデリングしているので, $p$は解析的に計算可能です.

$\alpha_{\rm CEI}(\boldsymbol{x})$を整理すると,

\begin{aligned}
\alpha_{{\rm CEI}} (\boldsymbol{x}) 
&= \mathbb{E}[\Delta(\boldsymbol{x}) \max(0, y - y_{\rm best})]
\\
&=\mathbb{E}[\Delta(\boldsymbol{x})] \mathbb{E}[\max(0, y - y_{\rm best})]
\\
&= p\cdot\alpha_{\rm EI}(\boldsymbol{x})
\end{aligned}

BoTorchの場合では, $\Delta(\boldsymbol{x})$をシグモイド関数で近似しています.

\Delta(\boldsymbol{x}) = -\sigma\left(
\frac{c(\boldsymbol{x})}{\eta}
\right)
  • $\sigma(z) = \frac{1}{1 + \exp(z)}$ : シグモイド関数
  • $c(\boldsymbol{x})$ : 制約関数モデルの出力
  • $\eta$ : 平滑化パラメータ(default = 1e-3)

BoTorchでの実装方法

BoTorchの獲得関数には, モンテカルロ獲得関数と解析的獲得関数なものが存在し, それぞれ実装方法が異なります.
この記事ではモンテカルロ獲得関数の場合をメインに取り上げています.

解析的獲得関数の場合

制約付きEIであれば, ConstrainedExpectedImprovementのように, 対応する獲得関数のクラスが用意されています.

内部では, $\Delta(\boldsymbol{x})$を解析的に計算していますが, ここでは詳細は省略します.

モンテカルロ獲得関数の場合

ModelListGPを利用し, 制約関数も合わせた複数の近似モデルを学習します.

import torch
from botorch.models import SingleTaskGP, ModelListGP
from gpytorch.mlls import SumMarginalLogLikelihood
from botorch import fit_gpytorch_mll

X = torch.Tensor([[0.4278, 0.6047],
        [0.3923, 0.2084],
        [0.4785, 0.9650],
        [0.8028, 0.6409],
        [0.2216, 0.9384],
        [0.3374, 0.9425],
        [0.1206, 0.8151]])
Y = torch.Tensor([[ -37.1342,   -6.8914],
        [ -18.5380,  -11.4081],
        [-132.8752,   -4.7968],
        [ -87.7746,   -5.6650],
        [ -34.4564,   -5.6988],
        [ -87.3948,   -5.3671],
        [  -0.4368,   -5.6471]])

model = SingleTaskGP(train_X, train_Y[:, 0:1])  # 目的関数モデル
model_c = SingleTaskGP(train_X, train_Y[:, 1:2])  # 制約関数モデル
model = ModelListGP(model, model_c)

# パラメータ推定
mll = SumMarginalLogLikelihood(model.likelihood, model)
fit_gpytorch_mll(mll)

Objectiveによる出力の変換

制約関数も合わせてモデリングしているので, 出力は2次元になっています.

X = torch.Tensor([[0.4, 0.6]])
with torch.no_grad():
    pred_mean = model.posterior(X).mean

print(pred_mean)
>> tensor([[-31.2329,  -6.9613]])

2つの出力のうち, どちらが目的関数モデルの出力なのかを明示して獲得関数に渡すために, Objectiveを利用します.

Objectiveクラスはモデルの出力を最適化対象となる関数に変換するためのモジュールです.

主な用途

  • ブラックボックス制約を考慮した最適化
  • 二つの目的関数の和を最小化
  • etc.　

今回は, モデル出力が2次元で1次元目を最適化対象にしたいので, シンプルに1次元目を返すように実装します.

from botorch.acquisition.objective import MCAcquisitionObjective

class CustomObjective(MCAcquisitionObjective):
    """ガウス過程の出力変換用.
    1次元目(index=0)を目的関数モデルの出力にとして返す.
    """

    def __init__(self):
        super().__init__()

    def forward(self, samples, X):
        return samples[..., 0]

obj = CustomObjective()
print(obj(pred))
>> tensor([-31.2329])

最適化で利用する際は, 獲得関数を定義するときにobjective引数へ渡します.

obj = CustomObjective()
acq_func = qExpectedImprovement(
                model=model,
                best_f=best_f,
                sampler=sampler,
                objective=obj,  # 目的関数モデルの出力を指定
            )

また, 今回は目的変数が1つの場合のモンテカルロ獲得関数の利用を前提としているので, MCAcquisitionObjectiveを継承してCustomObjectiveを実装しましたが, 用いる獲得関数によってベースクラスは異なるので注意してください.

例えば, 最適化対象の目的関数が2つで, 多目的ベイズ最適化のためのqExpectedHypervolumeImprovementを利用する際は, MCMultiOutputObjectiveを利用する必要があります.

constracts引数 or ConstrainedMCObjective

獲得関数によって, 推奨される制約条件式の渡し方が異なります.

constrains引数が存在する場合

(例) qExpectedImprovementなど

constrains引数が存在する獲得関数の場合は, 定義時に制約を満たす場合にマイナスになるよう定義した関数をconstracts引数に渡します. 例えば, $y_1 < 10$であれば, $c = -10 + y_1$とすれば, 制約を満たす場合は$c$はマイナスになります.

# Zはモデルの出力. 2次元目(index=1)が制約関数モデルの出力
constraint = lambda Z: -10 + Z[..., 1]  
acq_func = qExpectedImprovement(
                model=model,
                best_f=best_f,
                sampler=sampler,
                objective=obj,  # 目的関数モデルの出力を指定
                constraints=[constraint]  # 制約条件式の反映
            )

内部では, compute_smoothed_feasibility_indicator()を呼んで$\Delta(\boldsymbol{x})$を計算しています.
constracts引数がある場合は, 後述するConstrainedMCObjectiveの利用は非推奨です.

constrains引数がない場合

(例) qSimpleRegretなど

ConstrainedMCObjectiveを利用し, 最適化対象の目的関数の出力と制約関数を合わせて定義します.

from botorch.acquisition.objective import ConstrainedMCObjective

c_obj = ConstrainedMCObjective(
    objective=lambda Z: Z[..., 0],  # 目的関数
    constraints=[lambda Z: -10 + Z[..., 1]],  # 制約関数(制約を満たす場合マイナス)
)
acq_func = qSimpleRegret(
                model=model,
                sampler=sampler,
                objective=c_obj,  # 目的関数モデルの出力を指定
            )

将来的にはConstrainedMCObjectiveを利用した方法は非推奨となると思われます.

TODO: Deprecate this as default way to handle constraints with MC acquisition functions once we have data on how well SampleReducingMCAcquisitionFunction works.

実行例

$y_1$をBranin Function, $y_2$をCurrin Functionとしたテスト用関数を用いて, $y_1 > -10$ という制約条件の下で$y_2$を最大化する探索ループを実行してみます.

※ $y_1, y_2$にはトレードオフ関係が存在します.

初期点をランダムに5点取得し, 以降は制約付きqLogEIに基づいて探索を実行します.

import numpy as np
import torch
import japanize_matplotlib
from math import sqrt, log
from matplotlib import pyplot as plt

from botorch.test_functions.multi_objective import BraninCurrin as br
from botorch.utils.transforms import normalize, unnormalize
from botorch.fit import fit_gpytorch_mll
from botorch.models import SingleTaskGP
from botorch.models.model_list_gp_regression import ModelListGP
from botorch.models.transforms.outcome import Standardize
from botorch.optim import optimize_acqf
from gpytorch.mlls.sum_marginal_log_likelihood import SumMarginalLogLikelihood
from botorch.acquisition.objective import MCAcquisitionObjective
from botorch.sampling import SobolQMCNormalSampler
from botorch.acquisition.logei import qLogExpectedImprovement

SQRT2 = sqrt(2)
SQRT3 = sqrt(3)


class BraninCurrin:

    def __init__(self) -> None:
        tkwargs = {
            'dtype': torch.double,
            'device': torch.device('cuda' if torch.cuda.is_available() else 'cpu'),
        }
        self.problem = br(negate=True).to(**tkwargs)
        self.bounds = self.problem.bounds

    def f(self, xx: np.ndarray) -> np.ndarray:
        if xx.shape != (1, 2):
            raise InputError('入力次元エラー. shape=(1, 2) is required')
        xx = torch.from_numpy(xx)
        f = self.problem(xx).numpy().copy()
        return f

    def random_x(self) -> np.ndarray:
        """入力空間の点をランダムに1点取得. (初期点生成用)"""
        x = np.random.uniform(low=0.0, high=1.0, size=2)
        x = x.reshape(1, x.shape[0])
        return x


class CustomObjective(MCAcquisitionObjective):
    """ガウス過程の出力変換用.

    目的変数y1, y2に対して, y1は制約関数として扱うため, y2のみを返す.
    """

    def __init__(self):
        """"""
        super().__init__()

    def forward(self, samples, X):
        # y2を目的変数の値とする
        return samples[..., 1]


class BayesOptimizer:
    """ベイズ最適化実行クラス"""

    def __init__(self):
        """"""
        pass

    def get_candidates(self, Xs: torch.Tensor, Ys: torch.Tensor):
        # 目的変数のガウス過程
        ys = Ys[:, 1].unsqueeze(1)
        model = SingleTaskGP(Xs, ys, outcome_transform=Standardize(m=ys.size(-1)))
        # 制約関数のガウス過程
        cs = Ys[:, 0].unsqueeze(1)
        model_c = SingleTaskGP(Xs, cs, outcome_transform=Standardize(m=cs.size(-1)))
        # 複数のモデルを扱うためModelListを使う
        models = ModelListGP(model_c, model)
        mll = SumMarginalLogLikelihood(models.likelihood, models)
        # modelとmodel_cのハイパーパラメータの最適化
        fit_gpytorch_mll(mll)

        # ブラックボックス制約の定義. 制約(y1 > -10)を満たす場合, マイナスになるように定義
        constraints = [lambda Z: -10 - Z[..., 0]]

        # 現在の最良点を取得
        diffs = - 10 - cs[:, 0].squeeze()
        diffs[diffs < 0] = 0
        pass_indices = (diffs == 0).nonzero(as_tuple=True)[0].tolist()
        if len(pass_indices) > 0:
            # 制約条件を満たすものの中で最も良い(最大)ものをbest_fとして選択
            passed_ys = ys.squeeze()[pass_indices]
            best_f = torch.max(passed_ys, 0).values
        else:
            # 制約条件を満たすものがない場合, 最も制約条件に近いものをbest_fとして選択
            best_f = ys.squeeze()[torch.argmin(diffs).item()]

        # 獲得関数を定義
        sampler = SobolQMCNormalSampler(sample_shape=torch.Size([128]))
        obj = CustomObjective()
        qLogEI = qLogExpectedImprovement(
            model=models,
            best_f=best_f,
            sampler=sampler,
            objective=obj,  # 目的関数モデルの出力を指定
            constraints=constraints,  # 制約をここで渡す
        )

        # 獲得関数最大化
        X_dim = Xs.size()[1]
        bounds_norm = torch.zeros(2, X_dim)
        bounds_norm[1] = 1
        candidates, _ = optimize_acqf(
            acq_function=qLogEI,
            bounds=bounds_norm,
            q=1,
            num_restarts=10,
            raw_samples=512,
            options={'batch_limit': 5, 'maxiter': 200},
            sequential=True,
        )
        return candidates.detach()
    

def generate_init_data(target_f, sample_num: int = 10):
    """初期点の生成."""
    # 初期点ランダムに10点
    X_init = target_f.random_x()
    Y_init = target_f.f(X_init)
    for _ in range(sample_num - 1):
        X = target_f.random_x()
        y = target_f.f(X)
        X_init = np.concatenate([X_init, X])
        Y_init = np.concatenate([Y_init, y])
    X_init = torch.from_numpy(X_init)
    Y_init = torch.from_numpy(Y_init)
    return X_init, Y_init


###########################
# メインループ
###########################
NUM_ITER = 20
INIT_NUM = 5

target_f = BraninCurrin()
bounds = target_f.bounds

# 初期点生成
Xs, Ys = generate_init_data(target_f, sample_num=INIT_NUM)

# ベイズ最適化ループ
for i in range(NUM_ITER):
    optimizer = BayesOptimizer()
    # 説明変数正規化
    Xs_norm = normalize(Xs, bounds)
    # 実験候補点取得
    X_candidates = optimizer.get_candidates(Xs_norm, Ys)
    # 正規化を戻す
    X_candidates = unnormalize(X_candidates, bounds)
    Xs = torch.cat([Xs, X_candidates])
    print(X_candidates)

    # 観測 & 追加
    Y = torch.from_numpy(target_f.f(X_candidates.numpy()))
    Ys = torch.cat([Ys, Y])

# 結果プロット
colors = list(range(NUM_ITER + INIT_NUM))
fig = plt.figure(figsize=(15, 8))
plt.title('y2:最大化. ブラックボックス制約(y1 > -10)', fontsize=20)
plt.scatter(Ys[:, 0], Ys[:, 1], s=50, c=colors, cmap='viridis', label='non_const', edgecolor='k', alpha=0.5)
plt.colorbar(label='Iteration')
plt.xlabel('y1', fontsize=20)
plt.ylabel('y2', fontsize=20)
plt.vlines(x=-10, ymin=-15, ymax=0, linestyles='dashed', color='black')
plt.tight_layout()

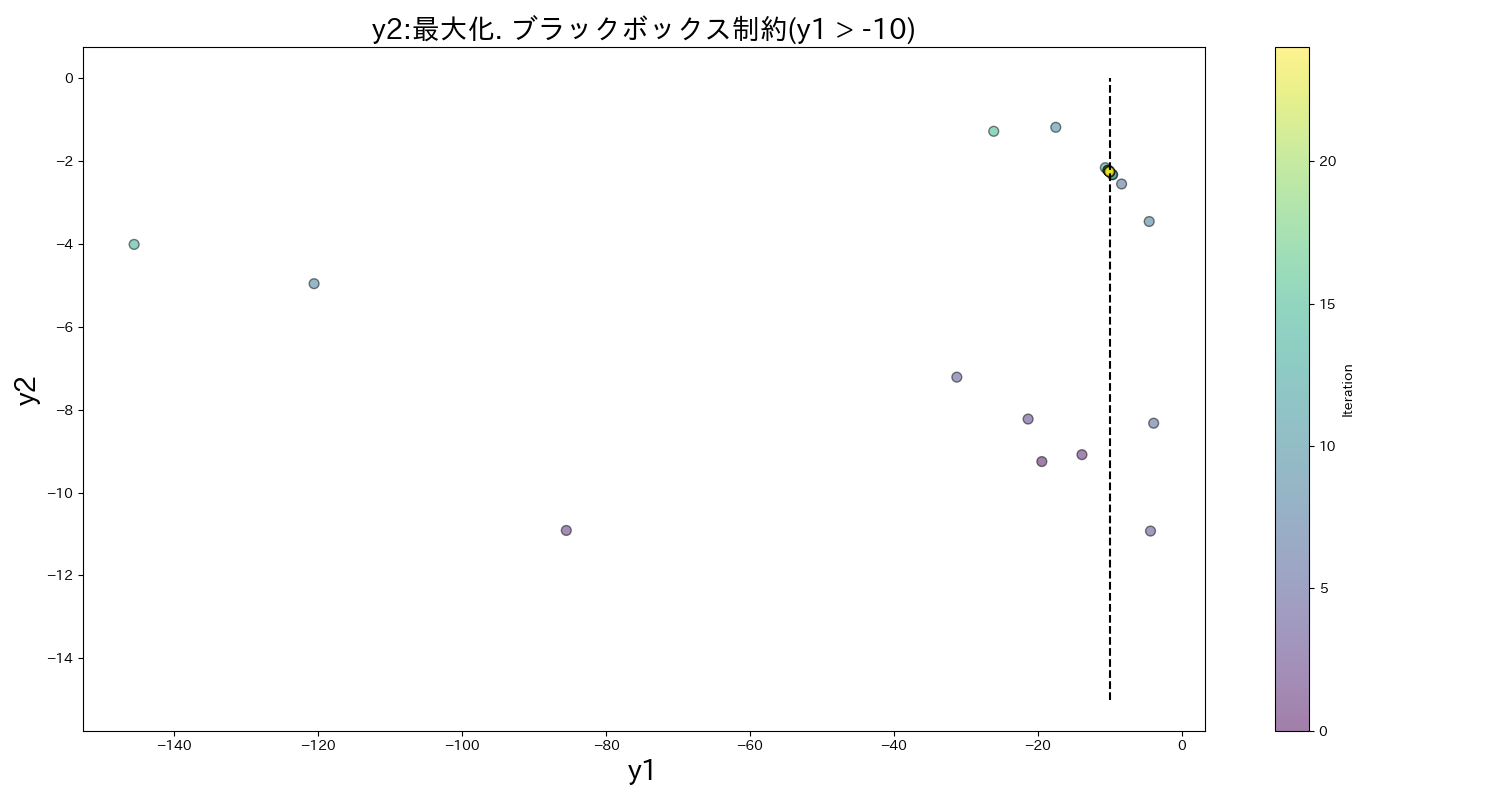
test.png
$y_1 > -10$を満たす可能性が高そうかつ$y_2$を最大化できる点を探索してくれてそうです.

参考文献

2
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?