はじめに
点過程は時系列解析でよく利用される手法です.
比較的短い時間で複数のイベントが集中して起こりやすいクラスター性を仮定した点過程を自己励起過程と呼びます.
この記事では,自己励起過程の一種であるHawkes過程のパラメータ推定をPythonで実装することを目的としています.
以下の一部を雑に実装してみた内容になってます. (点過程を勉強するならまず読むべき!)

点過程とは
その名の通り, 空間上にランダムに分布する「点」の集合に関する確率過程です.
時系列解析文脈で言えば, 「点」=「あるイベントの発生」になります.
イベントの発生時刻 $t_i$を確率変数と考えれば, 区間$[0, T]$におけるイベントの配置 $\boldsymbol{t}_n = \{t_1, \ldots, t_n \}$ は試行ごとに異なります.
点過程では, あるイベントの配置 $\boldsymbol{t}_n$ がどれほど発生しやすいかを確率密度関数 $p_{[0,T]}(\boldsymbol{t}_n)$ で表します.
点過程の一般形
一般形では, ある時刻 $t$ の直前のまでのイベントの発生履歴 $H_t = \{t_i|t_i<t\}$ が与えられたとき, 時刻$t$から微小時間$\Delta$まででイベントの発生確率を条件付き強度関数 $\lambda(t|H_t)$ を用いて $\lambda(t|H_t)\Delta$で表します.
細かい導出は省きますが, このとき観察期間 $[0, T]$ における条件付き強度 $\lambda(t|H_t)$ の点仮定の確率密度は以下になります.
p_{[0, T]}(\boldsymbol{t}_n) = \prod_{i=1}^n \lambda(t_i|H_{t_i}) \times \exp\left[- \int_0^T \lambda(s|H_s)ds \right]
※ 導出の詳細は点過程の時系列解析 (近江 崇宏・野村 俊一 著)に詳しく記載されています.
Hawkes過程
Hawkes過程は, イベントの発生しやすさを表す強度関数に以下のような条件付き強度関数を仮定した自己励起過程です.
\lambda(t|H_t) = \mu + \sum_{t_i < t}g(t-t_i)
ここで, $\mu$は非負の定数で $g(\cdot)$は過去のイベントからの影響を表すカーネル関数です.
つまり, ベースラインのイベント発生強度 $\mu$ と過去の各イベントからの影響の足し合わせです.
カーネル関数としては以下のような指数関数や冪関数がよく使われます.
g(\tau) = ab\exp(-b\tau)\\ g(\tau) = \frac{k}{(\tau + c)^p}
イベントが発生すると強度が一時的に上昇し, イベントが発生しやすくなることを仮定しています
こちらも詳細は省きますが, 観察期間$[0,T]$における条件付き強度 $\lambda(t|H_t)$ のHawkes過程の確率密度は以下のようになります.
p_{[0,T]}(\boldsymbol{t}_n) = \prod_{i=1}^n \left[\mu + \sum_{j < i}g(t-t_j)\right]
\times \exp\left[-\mu T - \sum_{i=1}^n\int_{t_i}^T g(s-t_i)ds \right]
Hawkes点過程のパラメータ推定
期間$[0, T]$において, イベントの観測データ$\boldsymbol{t}_n = \{t_1, \ldots, t_n \}$が $g(\tau) = ab\exp(-b\tau)$のHawkes過程に従っていると仮定し, パラメータを最尤推定で求めます.
推定するパラメータを $\boldsymbol{\theta} = \{\mu, a, b\}$すると, 尤度関数は $\mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) = p_{[0,T]}(\boldsymbol{t}_n| \boldsymbol{\theta}) $ です.
最尤推定値 $\hat{\boldsymbol{\theta}}$ は以下になります.
\begin{align}
\hat{\boldsymbol{\theta}}
&= \arg\max_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) \\
&= \arg\max_{\boldsymbol{\theta}} \log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n)
\end{align}
\log\mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) = \sum_{i=1}^n \log\left[ \mu + \sum_{j<i} ab\exp[-b(t_i - t_j)]\right] - \left[\mu T + \sum_{i=1}^n a[1-\exp[-b(T-t_i)]]\right]
これは解析的に求めることができないので, 勾配法による数値計算で推定します.
(※ 準ニュートン法の方が早いですが, 今回はめんどくさいのでシンプルに勾配法でやります)
各パラメータに関する勾配を計算すると以下のようになります.
\begin{align}
\frac{\partial}{\partial\mu}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) &= \sum_{i=1}^n \frac{1}{\mu + \sum_{j<i}ab\exp[-b(t_i-t_j)]} - T \\
\frac{\partial}{\partial a}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) &= \sum_{i=1}^n \frac{\sum_{j<i}b\exp[-b(t_i - t_j)] }{\mu + \sum_{j<i}ab\exp[-b(t_i-t_j)]} - \sum_{i=1}^n [1 - \exp[-b(T-t_i)]]\\
\frac{\partial}{\partial b}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) &= \sum_{i=1}^n \frac{\sum_{j<i} a\exp[-b(t_i - t_j)][1-b(t_i-t_j)]}{\mu + \sum_{j<i}ab\exp[-b(t_i-t_j)]} - \sum_{i=1}^n a(T-t_i) \exp[-b(T-t_i)]
\end{align}
これは単純に計算すると, $O(n^2)$の計算量がかかってしまいますが, 以下の計算上の工夫をすることで$O(n)$で計算することができます(すごい)
まずは, 勾配の式を以下のように変形します.
\begin{align}
\frac{\partial}{\partial\mu}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) &= \sum_{i=1}^n \frac{1}{\lambda_i} - T \\
\frac{\partial}{\partial a}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) &= \sum_{i=1}^n \frac{1}{\lambda_i}\frac{\partial\lambda_i}{\partial a} - \sum_{i=1}^n [1 - \exp[-b(T-t_i)]]\\
\frac{\partial}{\partial b}\log \mathcal{L}(\boldsymbol{\theta} | \boldsymbol{t}_n) &= \sum_{i=1}^n \frac{1}{\lambda_i}\frac{\partial\lambda_i}{\partial b} - \sum_{i=1}^n a(T-t_i) \exp[-b(T-t_i)]
\end{align}
このとき,
\begin{align}
\lambda_i &= \mu + \sum_{j<i}ab\exp[-b(t_i-t_j)] \\
\frac{\partial \lambda_i}{\partial a} &= \sum_{j<i}b\exp[-b(t_i - t_j)] \\
\frac{\partial \lambda_i}{\partial b} &= \sum_{j<i} a\exp[-b(t_i - t_j)][1-b(t_i-t_j)]
\end{align}
です. ここで,
G_i = \sum_{j < i} ab\exp[-b(t_i - t)]
とおくと, 以下の漸化式が成り立ちます.
\begin{aligned}
G_{i+1} &= (G_{i} + ab)\exp[-b(t_{i+1} - t_i)] \\
\frac{\partial G_{i+1}}{\partial b} &= \left(\frac{\partial G_{i}}{\partial b} + a\right) \exp[-b(t_{i+1} - t_i)] - G_{i+1}(t_{i+1}-t_i)
\end{aligned}
ただし, $G_1 = 0, \frac{\partial G_{1}}{\partial b} = 0$です.
これは再起的に計算可能であるため, 全て計算後に以下の関係式を用いて勾配を計算します.
\lambda_i = G_i + \mu,
\quad
\frac{\partial \lambda_i}{\partial a} = \frac{G_i}{a},
\quad
\frac{\partial \lambda_i}{\partial b} = \frac{\partial G_i}{\partial b}
実装
import numpy as np
class HawkesProcess:
"""
Hawkes過程
Attribution:
theta (np.arrray): Hawkes過程のパラメータ
"""
def __init__(self) -> None:
self.theta = np.array([0.01, 0.5, 0.5])
def fit(self, t, T) -> None:
"""
学習(負の対数尤度の最小化)
Args:
t: イベント発生時刻系列
T: 観測期間
"""
eta = 0.00001
t = t[t < T]
for i in range(1000):
# パラメータ更新
grad = self.nll_grad(t, T)
self.theta = self.theta - eta * grad
def nll_grad(self, t, T) -> np.array:
"""
負の対数尤度の勾配計算
Args:
t: イベント発生時刻系列
T: 観測期間
"""
mu = self.theta[0]
a = self.theta[1]
b = self.theta[2]
G = [0]
G_db = [0]
lam = [mu]
lam_da = [0]
lam_db = [0]
# 漸化式による変数の事前計算
for i in range(len(t) - 1):
G.append((G[i] + a * b) * np.exp(-b * (t[i + 1] - t[i])))
G_db.append((G_db[i] + a) * np.exp(-b * (t[i + 1] - t[i])) - G[i + 1] * (t[i + 1] - t[i]))
lam.append(G[i + 1] + mu)
lam_da.append(G[i + 1] / a)
lam_db.append(G_db[i + 1])
# 勾配の計算
x1, x2, x3, x4, x5 = 0, 0, 0, 0, 0
for i in range(len(t)):
x1 += (1 / lam[i])
x2 += (1 / lam[i]) * lam_da[i]
x3 += 1 - np.exp(-b * (T - t[i]))
x4 += (1 / lam[i]) * lam_db[i]
x5 += a * (T - t[i]) * np.exp(-b * (T - t[i]))
grad_mu = x1 - T
grad_a = x2 - x3
grad_b = x4 - x5
return np.array([-grad_mu, -grad_a, -grad_b])
import numpy as np
from hawkes import HawkesProcess
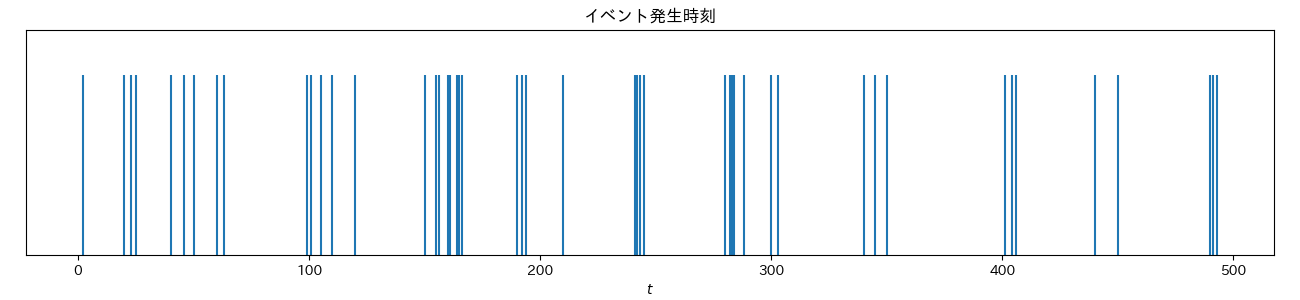
t = np.array([
2, 20, 23, 25, 40, 46, 50, 60, 63, 99, 101, 105, 110, 120, 150, 155, 156, 160, 161, 164, 165, 166, 190, 192, 194,
210, 241, 242, 243, 245, 280, 282, 283, 284, 288, 300, 303, 340, 345, 350, 401, 404, 406, 440, 450, 490, 491, 493
])
hawkes_process = HawkesProcess()
hawkes_process.fit(t, 300)
print(hawkes_process.theta)
[0.07386855 0.43402861 0.432499]
区間 $[0, 300]$の観測データを使ってパラメータを推定した結果, 以下のような推定値が得られました
$\mu = 0.07386855$
$a = 0.43402861$
$b = 0.432499$
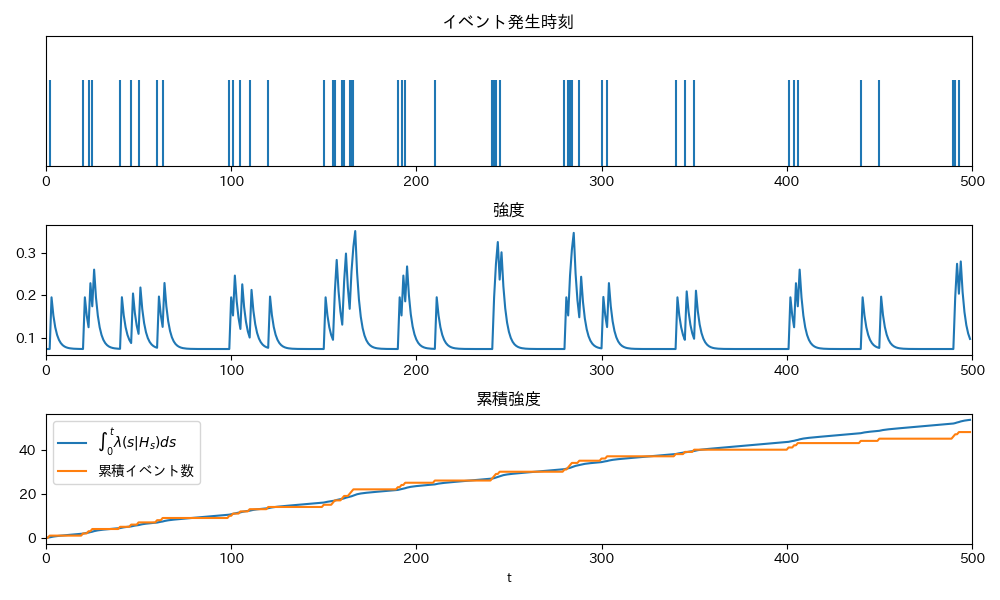
推定値を使って各時刻での強度と累積強度をプロットすると以下のようになりました.
学習時のステップサイズや終了条件などはかなり雑にやってますが, まあまあ妥当そうな結果になりましたね.