LoginSignup
7
5

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@dai08srhgin株式会社マイクロアド

BoTorch v0.12.0からデフォルトになったDim-scaled log-normal priorについて

Posted at

概要

ベイズ最適化の代理モデルとしてよく用いられるガウス過程回帰では，カーネル関数のパラメータの推定は最尤推定やMAP(最大事後確率)推定で行われることが一般的です．BoTorchではMAP推定を採用しています．

こちらのリリースノートにあるように，BoTorch 0.12.0からほとんどのモデルでMAP推定の際のlength-scaleの事前分布としてDim-scaled log-normal prior [Hvarfner, et al., 2024]がデフォルトで採用されるようになりました．

release 0.12.0

Update most models to use dimension-scaled log-normal hyperparameter priors by
default, which makes performance much more robust to dimensionality.

この記事では，MAP推定によるパラメータの推定と，Dim-scaled log-normal分布を事前分布とすることの効果について紹介します．

MAP推定によるカーネルのパラメータ推定

ガウス過程の導入

入力 $\boldsymbol{x}$ を基底関数ベクトル $\boldsymbol{\phi}(\cdot)$によって変換した特徴量ベクトルを考えます．

\boldsymbol{\phi}(\boldsymbol{x}) = (\phi_0(\boldsymbol{x}), \phi_1(\boldsymbol{x}), \ldots, \phi_H(\boldsymbol{x}))^{\top}

観測データ $\{(\hat{y}_i, \boldsymbol{x}_i)\}_{i=1}^{N}$ があるとき，重みベクトル $\boldsymbol{w} = (w_0, w_1, \ldots, w_H)^{\top}$ を用いて線形回帰モデルの行列表現を表すと以下のようになります．

\hat{\boldsymbol{y}} = \boldsymbol{\Phi}\boldsymbol{w}

\begin{aligned}
\underbrace{
\begin{pmatrix}
  \hat{y}_1\\
  \hat{y}_2\\
  \vdots \\
  \hat{y}_N\\
\end{pmatrix}
}_{\hat{\boldsymbol{y}}}
&= 
\underbrace{
\begin{pmatrix}
  \phi_0(\boldsymbol{x}_1) & \phi_1(\boldsymbol{x}_1) & \cdots & \phi_H(\boldsymbol{x}_1)\\

\phi_0(\boldsymbol{x}_2) & \phi_1(\boldsymbol{x}_2) & \cdots & \phi_H(\boldsymbol{x}_2)\\

  \vdots & & &\vdots \\

\phi_0(\boldsymbol{x}_N) & \phi_1(\boldsymbol{x}_N) & \cdots & \phi_H(\boldsymbol{x}_N)
\end{pmatrix}
}_{\boldsymbol{\Phi}}

\underbrace{
\begin{pmatrix}
  {w}_0\\
  {w}_1\\
  \vdots \\
  {w}_H\\
\end{pmatrix}
}_{\boldsymbol{w}}

\end{aligned}

ここで， $\boldsymbol{x}_1, \ldots, \boldsymbol{x}_N$ が与えられれば，計画行列 $\boldsymbol{\Phi}$ は定数行列であるため，基底関数回帰の解は線形回帰と同様の形になります．

\boldsymbol{w} = (\boldsymbol{\Phi}^{\top} \boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{\top}\hat{\boldsymbol{y}}

基底関数をうまく選べば複雑な非線形関数でも精度良く近似できますが，説明変数の次元が高くなるほどに用意しなければならない基底関数の数が増え，推定しなければならないパラメータ数が膨大になります（次元の呪い）

そこで，モデルパラメータ $\boldsymbol{w}$ の積分消去を考えます．
重みベクトル $\boldsymbol{w}$ が平均 $\boldsymbol{0}$, 分散共分散行列 $\lambda^2 \boldsymbol{I}$ の多変量ガウス分布に従うと仮定します．

\boldsymbol{w}\sim \mathcal{N}(\boldsymbol{0}, \lambda^2 \boldsymbol{I})

$\boldsymbol{w}$ がガウス分布に従うので， $\boldsymbol{y} = \boldsymbol{\Phi}\boldsymbol{w}$ もまたガウス分布に従います．この時の期待値と共分散行列はそれぞれ以下のようになります．

  • $\mathbb{E}[\boldsymbol{y}] = \boldsymbol{\Phi}\mathbb{E}[\boldsymbol{w}] = \boldsymbol{0}$
  • $\Sigma = \mathbb{E}[\boldsymbol{y}\boldsymbol{y}^{\top}] - \mathbb{E}[\boldsymbol{y}]\mathbb{E}[\boldsymbol{y}]^{\top} = \mathbb{E}[(\boldsymbol{\Phi}
    \boldsymbol{w})(\boldsymbol{\Phi}\boldsymbol{w})^{\top}] = \lambda^2 \boldsymbol{\Phi\Phi}^{\top}$

以上より， $\boldsymbol{y}$ は以下の多変量ガウス分布に従います．

\boldsymbol{y} \sim\mathcal{N}(\boldsymbol{0}, \lambda^2\boldsymbol{\Phi\Phi}^{\top})

このように，特定の関数形を指定することなく確率的なモデリングができました．
これがガウス過程回帰モデルです．

$f$のガウス過程モデル

関数$f : \mathcal{X}\rightarrow \mathbb{R}$ がガウス過程に従うとは，任意の$N$個の入力ベクトル$(\boldsymbol{x}_1,\ldots,\boldsymbol{x}_N) \in\mathcal{X}$に対して，関数値ベクトル$\boldsymbol{f}=(f(\boldsymbol{x}_1), \ldots, f(\boldsymbol{x}_N))$の同時分布が，平均ベクトル$\boldsymbol{m}$, 共分散行列$\boldsymbol{\rm K}$の多変量ガウス分布に従うことを指す．

f \sim \mathcal{GP}(\boldsymbol{m}, \boldsymbol{\rm K})

カーネル関数とカーネルトリック

共分散行列 $\boldsymbol{\rm K} = \lambda^2\boldsymbol{\Phi\Phi}^{\top}$ の $(i, i')$ 成分は ${\rm K}_{i, i'} = \lambda^2 \boldsymbol{\phi}(\boldsymbol{x}_i)^{\top} \boldsymbol{\phi}(\boldsymbol{x}_{i'}) $ になります．

このことから，入力 $\boldsymbol{x}_i, \boldsymbol{x}_{i'}$ の特徴量変換 $\boldsymbol{\phi}(\boldsymbol{x}_i),\boldsymbol{\phi}(\boldsymbol{x}_{i'})$ を明示的に書き下さなくても，以下のような $\boldsymbol{x}_i$, $\boldsymbol{x}_{i'}$ の関係を返すカーネル関数 $k(\boldsymbol{x}_{i}, \boldsymbol{x}_{i'})$ を設計することで直接計算することができます．

k(\boldsymbol{x}_i, \boldsymbol{x}_{i'}) = \boldsymbol{\phi}(\boldsymbol{x}_i)^{\top}\boldsymbol{\phi}(\boldsymbol{x}_{i'})

これをカーネルトリックと呼びます．また $\boldsymbol{\rm K}$ をカーネル行列とも呼びます．

カーネル関数はガウス過程モデルの性質を決定する．
(カーネル関数を変化させることでモデルの表現力などを変化させられる．)

ガウス過程回帰はノンパラメトリックモデルですが，カーネル関数は通常パラメータを持つパラメトリック関数が利用されます．
RBF(二乗指数)カーネルの例

k(\boldsymbol{x} ,\boldsymbol{x}') 
= \exp
\left(
-\sum_{j=1}^d \frac{(x_j - x_j')^2}{2l^2}
\right), \quad\boldsymbol{x}, \boldsymbol{x}' \in\mathbb{R}^d

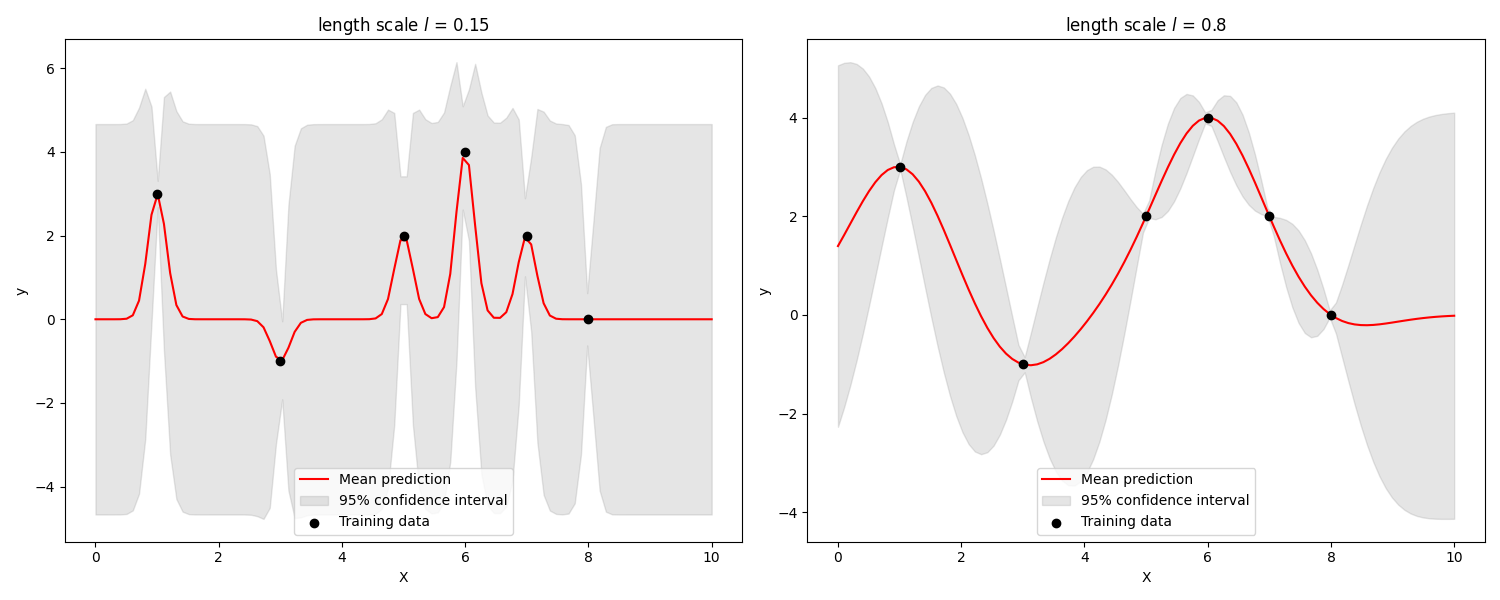
RBFカーネルの場合はlength scale $l$ がハイパーパラメータになり，どれだけ遠いデータを類似とみなすかを調整しています．

※ 上記は一般的なRBFカーネルの例で，ARD(Automatic Relevance Determination)の場合は次元ごとに異なるlength scale $l_i$を持ちます．（ベイズ最適化の利用シーンにおいては，重要な説明変数が判明していない状況が想定されるのでARDカーネルの利用が一般的です．）

パラメータの違いによってもモデルの複雑さが変化します．
rbf_sample.png

ガウス過程回帰の学習では，このカーネル関数のハイパーパラメータが推定(学習)対象になり，最尤推定やMAP推定で行われることが一般的です．

ここでは，BoTorchで採用されているMAP(最大事後確率)推定について説明します．

パラメータのMAP推定

ガウス過程は，パラメータ集合 $\boldsymbol{\theta}$ で決まるカーネル行列 $\boldsymbol{\rm K}_{\boldsymbol{\theta}}$ によって定まるガウス分布に従うので，尤度 $p(\boldsymbol{y} | \boldsymbol{X}, \boldsymbol{\theta})$ は以下のようになります．

\begin{aligned}
p(\boldsymbol{y} | \boldsymbol{X}, \boldsymbol{\theta}) &= \mathcal{N}(\boldsymbol{0}, \boldsymbol{\rm K}_{\boldsymbol{\theta}}) \\

&= \frac{1}{(2\pi)^{\frac{N}{2}} |\boldsymbol{\rm K}_{\boldsymbol{\theta}}|^{\frac{1}{2}}}
\exp 
\left(
- \frac{1}{2} \boldsymbol{y}^{\top}\boldsymbol{\rm 
 K}_{\boldsymbol{\theta}}^{-1}\boldsymbol{y}
\right)
\end{aligned}

推定したいパラメータ $\boldsymbol{\theta}$ の事前分布を $p(\boldsymbol{\theta})$ としたとき，観測データの下での $\boldsymbol{\theta}$ の事後分布は，ベイズの定理により以下のようになります．

\begin{aligned}
p(\boldsymbol{\theta} | \boldsymbol{y}, \boldsymbol{X}) = \frac{p(\boldsymbol{y}|\boldsymbol{X}, \boldsymbol{\theta})p(\boldsymbol{\theta})}{p(\boldsymbol{y} | \boldsymbol{X})}
\\
p(\boldsymbol{y}|\boldsymbol{X}) = \int p(\boldsymbol{y}|\boldsymbol{X}, \boldsymbol{\theta})p(\boldsymbol{\theta})d\boldsymbol{\theta}
\end{aligned}

MAP推定では，事後確率が最大になる値が推定値となります．上記の式において，分母は $\boldsymbol{\theta}$ に依存しないので，MAP推定値は以下のようになります．

\hat{\boldsymbol{\theta}} = \arg\max_{\boldsymbol{\theta}}
p(\boldsymbol{y}|\boldsymbol{X}, \boldsymbol{\theta})p(\boldsymbol{\theta})

このとき，事前分布 $p(\boldsymbol{\theta})$ は事前知識を考慮した上で，自分で設定することになります．また，一般的には推定したいパラメータは複数になりますが，それぞれ個別で事前分布を設定することができ，以下のように表現できます．

p(\boldsymbol{\theta}) = p(\theta_1)p(\theta_2)\cdots p(\theta_n)

BoTorchでは，これを勾配法で最適化しています．

BoTorchでの設定 (v0.12.0よりも前)

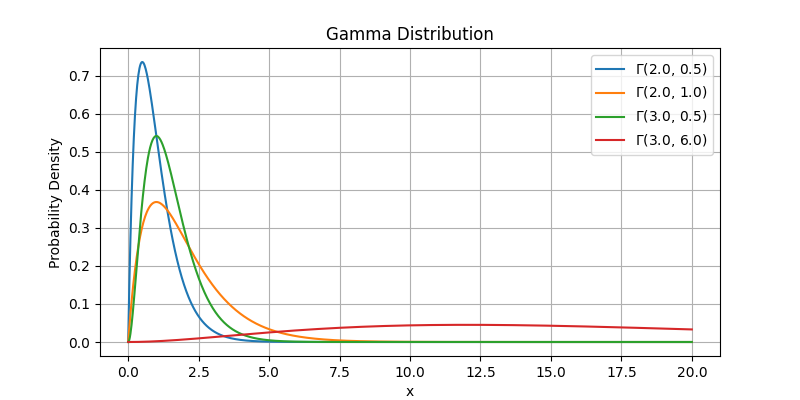
BoTorchでの一般的なGPモデルクラスであるSingleTaskGPでは，v0.12.0よりも前は引数のcovar_moduleを指定しない場合は，内部ではget_matern_kernel_with_gamma_prior()が呼び出されていました．

Constructs the Scale-Matern kernel that is used by default by several models. This uses a Gamma(3.0, 6.0) prior for the lengthscale and a Gamma(2.0, 0.15) prior for the output scale.

def get_matern_kernel_with_gamma_prior(
    ard_num_dims: int, batch_shape: Optional[torch.Size] = None
) -> ScaleKernel:
    r"""Constructs the Scale-Matern kernel that is used by default by
    several models. This uses a Gamma(3.0, 6.0) prior for the lengthscale
    and a Gamma(2.0, 0.15) prior for the output scale.
    """
    return ScaleKernel(
        base_kernel=MaternKernel(
            nu=2.5,
            ard_num_dims=ard_num_dims,
            batch_shape=batch_shape,
            lengthscale_prior=GammaPrior(3.0, 6.0),
        ),
        batch_shape=batch_shape,
        outputscale_prior=GammaPrior(2.0, 0.15),
    )

Source

上記のように，デフォルトではMatern-2/5カーネルのlength scaleの事前分布にはガンマ分布が用いられています．
gamma.png

Dim-scaled log-normal prior

ベイズ最適化は説明変数の次元数が20を超えてくると性能が大きく低下することが経験的に知られています．
Dim-scaled log-normal prior [Hvarfner, et al., 2024]は，高次元ベイズ最適化に対するアプローチとして提案された手法で，次元数に合わせて自動で調整される事前分布になっており，BoTorch v0.12.0からはデフォルトになっています．

ここでは簡単に論文の内容を紹介します．

モチベーション

本論文では，高次元ベイズ最適化がうまくいかないのは過度に複雑なガウス過程モデルが構築されることで観測したデータの情報がいかせていないことが原因であり，複雑さを制御できれば一般的なベイズ最適化でも機能すると主張している．

※ ここでの一般的なベイズ最適化は，RBFやMatarnをベースとしたARDカーネルを用いたガウス過程モデルを代理モデルとしたベイズ最適化を指しています．

モデルの複雑さを定量的に確認するために，最大情報利得 (MIG; Maximal Information Gain)を導入します．ガウス過程モデルとデータ集合$\boldsymbol{X}$に対する情報利得 $\rm IG$ を次のように定義します．

{\rm IG} (y_{\boldsymbol{X}}, f_{\boldsymbol{X}}) = \frac{1}{2}\log |\boldsymbol{I} + \sigma_{\varepsilon}^2 \boldsymbol{\rm K}|

$\boldsymbol{\rm K} = k(\boldsymbol{X}, \boldsymbol{X})$はカーネル行列です．
サンプル数 $|\boldsymbol{X}_n| = n$が固定された下での，MIG $\gamma_n$は最大の情報利得として次のように定義されます．

\gamma_n =max_{\boldsymbol{X}_n \subset \mathcal{X}} {\rm IG} (y_{\boldsymbol{X}_n}, f_{\boldsymbol{X}_n})

つまり，最も$\rm IG$が大きくなるようにサンプルを$n$個選択したときの値になります．
サンプルが独立($\boldsymbol{{\rm K}} \approx \boldsymbol{I}$)しているとき，MIGは最大になります．

次の図は，length scaleとMIGの関係を表しています．

length scale $l=0.03$の場合，ガウス過程モデルは非常に複雑になっており，MIGは$n=20$まで線型に増加しています．これは，サンプルを20点観測しても，収集されたデータとほぼ独立な領域が探索空間上に存在することになり，最適化が困難ということを意味しています．

次の図は，length scaleを固定したRBFカーネルを用いた時の次元数$D$とMIGの推移を表しています．

次元 $D=24$では， $k(\boldsymbol{X}_{5000}, \boldsymbol{X}_{5000}) \approx \boldsymbol{I}$であり， 5000サンプルでもRBFカーネルによるカーナる行列と独立したカーネル行列を区別するに不十分であり，ガウス過程によるモデリングがほとんど情報を提供しないことを示唆しています．

上記から，高次元ベイズ最適化におけるガウス過程モデルは複雑性の扱いが重要と分かります．

提案手法

次元数が増加してもほぼ一定の複雑性を維持したい

→ 問題の次元数に応じてlength scaleの事前分布を調整

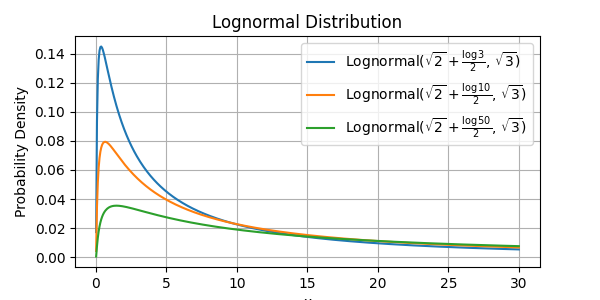
平均項を次元数$D$に応じてスケーリングさせた以下のような対数正規分布をlength scaleの事前分布に利用します．

l_i \sim {\rm LN}\left(\mu_0+ \frac{\log(D)}{2}, \sigma_0\right)

ここで，$\mu_0, \sigma_0$ はハイパーパラメータです．(デフォルト：$\mu_0 = \sqrt{2}$, $\sigma_0=\sqrt{3}$)

ln.png

[Koppen, 2000]で，次元数$D$の超立方体上でランダムサンプリングされた点の距離は$\sqrt{D}$に比例すると示されています．$l_i \propto \sqrt{D}$の速度で増加させることで，距離の増加による複雑性を打ち消すことが狙いになっています．

また，あくまで事前分布の調整であり，length scaleが決定的になるわけではないため，MAP推定によって$l_i$を逐次調整しながら他の変数よりも重要な変数を発見することが可能です．

BoTorch v0.12.0からは，デフォルトではget_covar_module_with_dim_scaled_prior()が内部で呼び出されているようです．

候補点取得の一連の処理を書くと以下のようになると思います．

train_x = normalize(train_x, bounds=bounds)  # 説明変数正規化

# 対数正規分布を事前分布に指定したガウス過程モデル定義
ard_num_dims = train_x.shape[-1]
lengthscale_prior = LogNormalPrior(loc=SQRT2 + log(ard_num_dims) * 0.5, scale=SQRT3)
covar_module = ScaleKernel(
    base_kernel=MaternKernel(
        nu=2.5,
        ard_num_dims=ard_num_dims,
        batch_shape=None,
        lengthscale_prior=lengthscale_prior,
        lengthscale_constraint=GreaterThan(2.500e-02),
    ),
    batch_shape=None,
    outputscale_prior=GammaPrior(2.0, 0.15),
)
model = SingleTaskGP(
    train_x, train_obj, outcome_transform=Standardize(m=train_obj.size(-1)), covar_module=covar_module
)

# パラメータ推定
mll = ExactMarginalLogLikelihood(model.likelihood, model)
fit_gpytorch_mll(mll)

# 獲得関数定義
sampler = SobolQMCNormalSampler(sample_shape=torch.Size([128]))
acq_func = qLogExpectedImprovement(model=model, best_f=train_obj.max(), sampler=sampler)

# 獲得関数の最適化
standard_bounds = torch.zeros_like(bounds)
standard_bounds[1] = 1
candidates, _ = optimize_acqf(
    acq_function=acq_func,
    bounds=standard_bounds,
    q=1,
    num_restarts=10,
    raw_samples=512,
    options={'batch_limit': 5, 'maxiter': 200},
    sequential=True,
)
candidates = unnormalize(candidates.detach(), bounds=bounds)

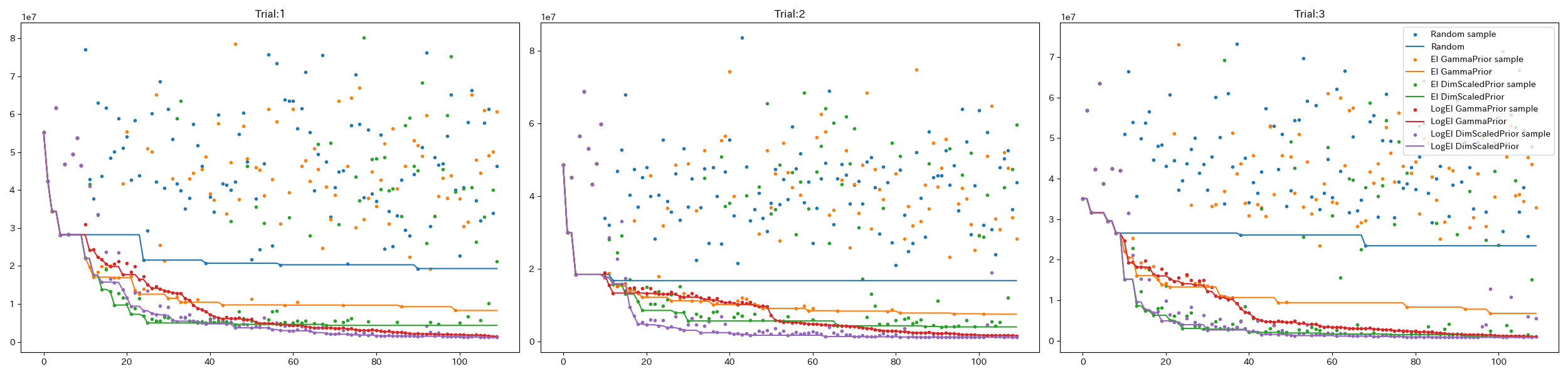
比較実験

比較的シンプルな関数形ですが，次元数を調整可能なベンチマーク関数としてSum Squares Functionの最小値探索を行います．

f(\boldsymbol{x}) =\sum_{i=1}^{D} i x_i^2

実験は$D=40$で行いました．
初期点はランダムに10点取得し，以降は各手法ごとに1点ずつ探索してます．実験は3回初期点を変えて行っており．その平均で評価しています．

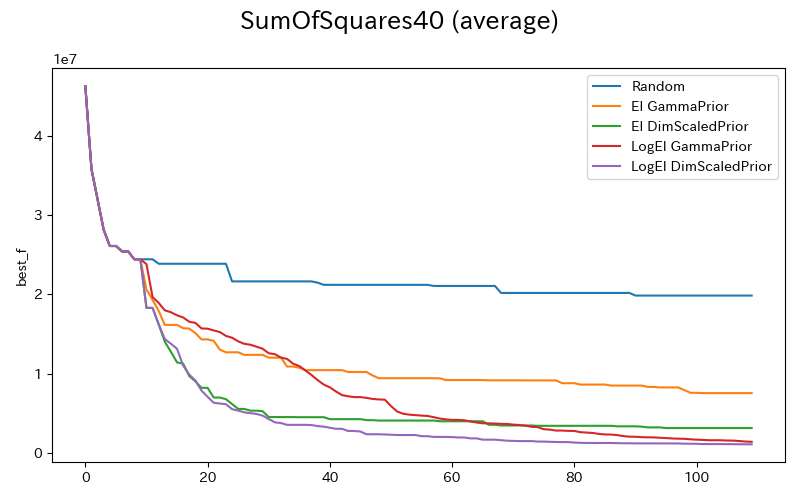
ファイル名

以下は各施行での探索点の推移です．
SumOfSquares40_all-2.png

上記Dim-scaled log-normal priorのパフォーマンスが優れていることが確認できました．ついでにLogEIがEIと比較して高性能なことも確認できます．(値消失に伴うランダム探索が無くなってますね．)

今回の実験も含め，他の獲得関数のテストなどもこちらのリポジトリで管理をしてます．

参考文献

7
5
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
5

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?