Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@daddygongon

Least square fitting by SVD

Last updated at Posted at 2023-01-20

svd fitting

cc by Shigeto R. Nishitani, 2023

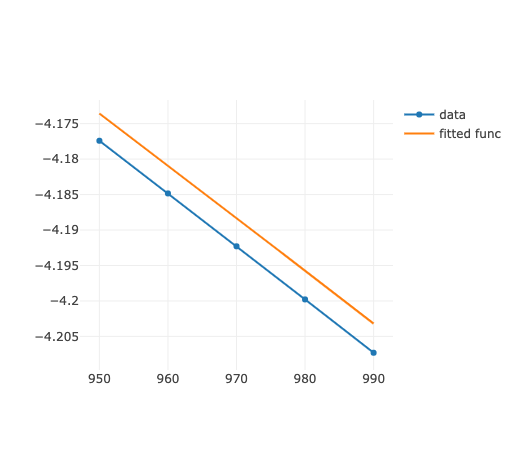
簡単な最小二乗法によるfittingでも計算誤差が出てしまうという例です．0からだいぶ離れたところで，微妙なエネルギー差をfittingしようとして出てきました．

結論はSVD(single value decomposition, 特異値分解)を使えというNumRecipeの教えを再確認．．．やれやれ．

最初のうまくいってない結果

  • include NumericCalcs
  • fit
  • plot

Ruby module for Numerical calculations

  require "matrix"
  require "rbplotly"

  module NumericCalcs
    include Math

    def fitting(x, d_y, dim = 3)
      y = d_y

      # make design matrix
      n, m = x.size, dim

      av = Matrix.zero(n, m)
      yy = Vector.zero(n)
      n.times do |i|
        m.times do |j|
          av[i,j] = x[i] ** j
        end
        yy[i] = y[i]
      end

      # calc inverse for non-square matrix
      ai = (av.transpose * av).inv
      b = av.transpose * yy
      return ai * b
    end

    def polynomials(coeffs, x)
      sum = 0.0
      coeffs.each_with_index do |c, i|
        sum += c * x ** i
      end
      sum
    end

    # x_ticks
    def mk_x(init, fin, dev) 
      x = []
      (init..fin).step(dev) { |i| x << i }
      x
    end

    def plot_data_and_func(xx, y_vals, func)
      dev = (xx.max - xx.min) / 100.0
      xx2 = mk_x(xx.min, xx.max, dev)

      traces = [{ x: [], y: [], name: "data" },
                { x: [], y: [], name: "fitted func" }]

      xx.size.times do |i| # rev for Numo::DFloat
        traces[0][:x] << xx[i]
        traces[0][:y] << y_vals[i]
      end

      xx2.each do |x|
        traces[1][:x] << x
        traces[1][:y] << func.call(x)
      end
      pl = Plotly::Plot.new(data: traces)
      Plotly.default_auth()
      return pl
    end
  end

  include NumericCalcs

#<Module:0x000000013e3cd518>

  p x_vals = [950, 960, 970, 980, 990]
  p y_vals = [-4.177412829697432, -4.1848393364765, -4.192296922237924, 
      -4.199785335389045, -4.207304330283102]

[950, 960, 970, 980, 990]
[-4.177412829697432, -4.1848393364765, -4.192296922237924, -4.199785335389045, -4.207304330283102]





[-4.177412829697432, -4.1848393364765, -4.192296922237924, -4.199785335389045, -4.207304330283102]

main results

  xx=x_vals
  yy = y_vals
  p vals=fitting(xx, yy, 4)

  f_plot = lambda { |x| polynomials(vals, x) }
  pl = plot_data_and_func(xx, yy, f_plot)
  pl.show
  #pl.savefig('./figs/fit_plot0.png')

Vector[-3.650146484375, -0.0003299713134765625, -2.7194619178771973e-07, 4.1382008930668235e-11]

./figs/fit_plot0.png

というのが default 計算の結果． これを改善できないかという話．

少し試行錯誤

明らかにずれていて，Maple の fitting を使うとばっちり．NumericCalcs::fitting が甘いのはあきらかだが，どうすれば．．．

  av = Matrix[[1, 950, 902500, 857375000], [1, 960, 921600, 884736000], [1, 970, 940900, 912673000], [1, 980, 960400, 941192000], [1, 990, 980100, 970299000]]
  yy = Vector[-4.177412829697432, -4.1848393364765, -4.192296922237924, -4.199785335389045, -4.207304330283102]

  ai = (av.transpose * av).inv
  b = av.transpose * yy
  ai * b

Vector[-3.650146484375, -0.0003299713134765625, -2.7194619178771973e-07, 4.1382008930668235e-11]

すると確かに．おなじ．

でも，これを Maple でやるとまた違った答え

[-3.650634765625, -0.0003314018249511719, -0.2756714821*10^(-6), 0.4160938261*10^(-10)])

になる．これは，数値誤差(Ruby の inv かな)のようなんで，放置．

1000->1 に(効果なし)

  x_vals2 = [950, 960, 970, 980, 990]
  x_vals2.map!{|val| val/1000.0}
  y_vals = [-4.177412829697432, -4.1848393364765, -4.192296922237924, 
      -4.199785335389045, -4.207304330283102]

[-4.177412829697432, -4.1848393364765, -4.192296922237924, -4.199785335389045, -4.207304330283102]

  xx=x_vals2
  yy = y_vals
  vals=fitting(xx, yy, 4)

  f_plot = lambda { |x| polynomials(vals, x) }
  pl = plot_data_and_func(xx, yy, f_plot)
  pl.show
  #pl.savefig('./figs/fit_fail1.png')

./figs/fit_plot1.png

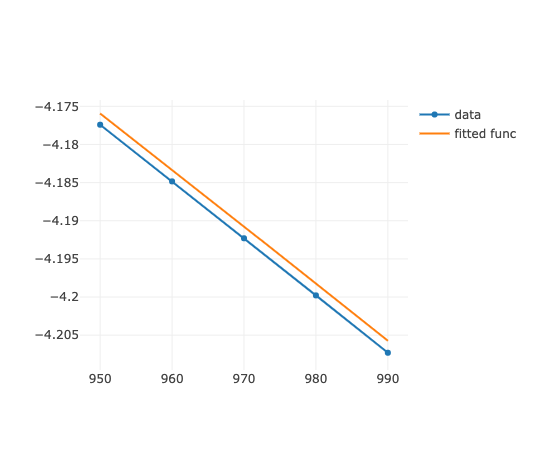
ちょっと変わりますが，差は大きいです．

Ruby の svd

Numo の導入

steep なんやろな．なら，SVD だが．Ruby にあったっけ？

  > gem install ruby-svd
  > emacs /Users/bob/.rbenv/versions/3.0.2/lib/ruby/gems/3.0.0/extensions/arm64-darwin-20/3.0.0/ruby-svd-0.5.1/gem_make.out

うーーん．gccのcompile エラー．

numo がそのまま動いた．へぇ，やるね．2年ほど前に動かなんでNumoを使ったコードをMatrixに書き換えたんですが．．．

どこが対応したんやろ．．． -Adddynamic_lookup linker option for macOS and Ruby3.1と４ヶ月ほど前に修正したはります

  require 'numo/gnuplot'
  require 'numo/narray'
  require 'numo/linalg'

  x, y=x_vals, y_vals

  # make design matrix
  n = 5 # data
  m = 4 # dimension
  av = Numo::DFloat.zeros(n, m)
  yy = Numo::DFloat.zeros(n)
  n.times do |i|
    m.times do |j|
      av[i,j]=x[i]**j
    end
    yy[i] = y[i]
  end

  # fit by using matrix inv
  p ai = Numo::Linalg.inv(Numo::Linalg.dot(av.transpose,av))
  p b = Numo::Linalg.dot(av.transpose,yy)
  $vars = Numo::Linalg.dot(ai,b)
  p ['$vars', $vars]

  # block for lazy evaluation in plot_data_and_func
  free_e_plot = lambda { |x| polynomials($vars, x) }

  pl = plot_data_and_func(x, y, free_e_plot)
  pl.show

Numo::DFloat#shape=[4,4]
[[5.78259e+10, -1.7888e+08, 184428, -63.3749], 
 [-1.7888e+08, 553356, -570.525, 0.196052], 
 [184428, -570.525, 0.588234, -0.00020214], 
 [-63.3749, 0.196052, -0.00020214, 6.94638e-08]]
Numo::DFloat#shape=[4]
[-20.9616, -20333.5, -1.97284e+07, -1.91454e+10]
["$vars", Numo::DFloat#shape=[4]
[-3.64941, -0.000331879, -2.73809e-07, 4.18368e-11]]

./figs/fit_plot2.png

少し変わってるのも(Matrix計算精度が)気になるけど，まあ，変わらんはね．

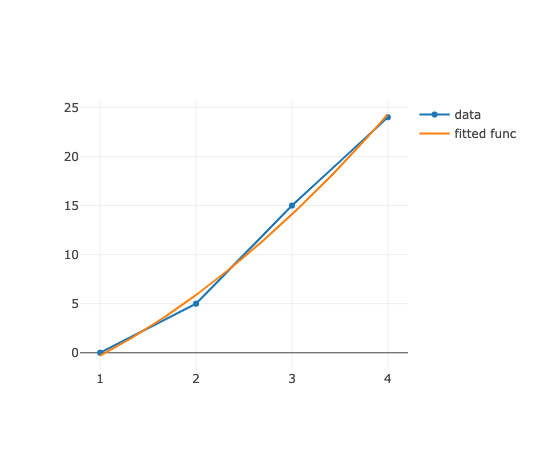
Numoの動作確認

SVDでの実装ですが，先ずは，講義のサイトから確実に動くのを取り出して，確認．

  x = Numo::NArray[[1,2,3,4]]
  y = Numo::NArray[[0,5,15,24]]

  fitting(x,y)

Vector[(-9/2), (16/5), (1/1)]


  x = Numo::NArray[[1,2,3,4]]
  y = Numo::NArray[[0,5,15,24]]

  # make design matrix
  n, m = 4, 3 # data, dimension
  av = Numo::DFloat.zeros(n, m)
  yy = Numo::DFloat.zeros(n)
  n.times do |i|
    m.times do |j|
      av[i,j]=x[i]**j
    end
    yy[i] = y[i]
  end

  # fit by using matrix inv
  require 'numo/linalg'
  ai = Numo::Linalg.inv(Numo::Linalg.dot(av.transpose,av))
  b = Numo::Linalg.dot(av.transpose,yy)
  vars = Numo::Linalg.dot(ai,b)
  p vars

  # block for lazy evaluation in plot_data_and_func
  y_fit = lambda { |x| polynomials(vars, x) }
  pl = plot_data_and_func(x, yy, y_fit)
  pl.show

Numo::DFloat#shape=[3]
[-4.5, 3.2, 1]

./figs/fit_plot3.png

Numo の svd の出力順は python と違う

numpy.linalg.svdにある通り，

a : (m,n array)
u,s,vh = linalg.svd(a)で
u : (m , m)
s : (k) よくわかってないよね．．．
vh : (n, n)

ところが Numo::Linalg.svd では，

s,u,vh = Numo::LInalg.svd(a)
s : k
u : m x m
vh : n x n

という感じ．

これに関するマニュアルはなさそう．ソースが

  l.323 Lapack.call(:gesdd, a, jobz:job)[0..2]

となってなるんで，s,u,vの順で正しそう．vは$v^T$とか書いてあったような．．． 確認して使わないと．

  ss, uu, vs =  Numo::Linalg.svd(av)

  iS = Numo::DFloat.zeros(m, n)
  m.times do |j|
      iS[j,j]=1.0/ss[j]
  end
  p iS

  p left = Numo::Linalg.dot(vs.transpose,iS)
  p right = Numo::Linalg.dot(uu.transpose,yy)

  Numo::Linalg.dot(left, right)

Numo::DFloat#shape=[3,4]
[[0.0509649, 0, 0, 0], 
 [0, 0.584088, 0, 0], 
 [0, 0, 3.75583, 0]]
Numo::DFloat#shape=[3,4]
[[-0.00421136, -0.393889, 2.75587, 0], 
 [-0.0138812, -0.404752, -2.50719, 0], 
 [-0.0488569, 0.14895, 0.474791, 0]]
Numo::DFloat#shape=[4]
[-28.6152, 1.83564, -1.41424, 1.34164]





Numo::DFloat#shape=[3]
[-4.5, 3.2, 1]

係数は，invを使ったのからsvdを使ったのに変えても一致．

実働の確認

元のデータでinvを使ったのをまずは確認．

  x, y=x_vals, y_vals

  # make design matrix
  n = 5 # data
  m = 4 # dimension
  av = Numo::DFloat.zeros(n, m)
  yy = Numo::DFloat.zeros(n)
  n.times do |i|
    m.times do |j|
      av[i,j]=x[i]**j
    end
    yy[i] = y[i]
  end

  # fit by using matrix inv
  require 'numo/linalg'
  ai = Numo::Linalg.inv(Numo::Linalg.dot(av.transpose,av))
  b = Numo::Linalg.dot(av.transpose,yy)
  $vars = Numo::Linalg.dot(ai,b)
  p ['$vars', $vars]

  # block for lazy evaluation in plot_data_and_func
  free_e_plot = lambda { |x| polynomials($vars, x) }

  pl = plot_data_and_func(x, y, free_e_plot)
  pl.show

["$vars", Numo::DFloat#shape=[4]
[-3.64941, -0.000331879, -2.73809e-07, 4.18368e-11]]

./figs/fit_plot2.png

  ss, uu, vs =  Numo::Linalg.svd(av)

  iS = Numo::DFloat.zeros(m, n)
  m.times do |j|
      iS[j,j]=1.0/ss[j]
  end
  #p iS
  left = Numo::Linalg.dot(vs.transpose,iS)
  right = Numo::Linalg.dot(uu.transpose,yy)

  p vars = Numo::Linalg.dot(left, right)

  # block for lazy evaluation in plot_data_and_func
  free_e_plot = lambda { |x| polynomials(vars, x) }

  pl = plot_data_and_func(x, y, free_e_plot)
  pl.show

Numo::DFloat#shape=[4]
[-3.65027, -0.000331299, -2.74726e-07, 4.14365e-11]

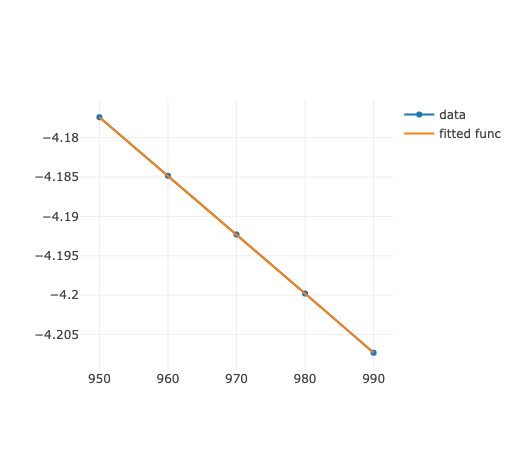
./figs/fit_plot4.png

さすが svd.

最終形（完成版fitting_svd)

  require 'numo/gnuplot'
  require 'numo/narray'
  require 'numo/linalg'

  def fitting_svd(x, d_y, dim = 3)
    y = d_y

    # make design matrix
    n, m = x.size, dim
    av = Numo::DFloat.zeros(n, m)
    yy = Numo::DFloat.zeros(n)
    n.times do |i|
      m.times do |j|
        av[i,j]=x[i]**j
      end
      yy[i] = y[i]
    end
    ss, uu, vs =  Numo::Linalg.svd(av)

    iS = Numo::DFloat.zeros(m, n)
    m.times do |j|
      iS[j,j]=1.0/ss[j]
    end
    #p iS
    left = Numo::Linalg.dot(vs.transpose,iS)
    right = Numo::Linalg.dot(uu.transpose,yy)

    return Numo::Linalg.dot(left, right)
  end

:fitting_svd

  p x_vals = [950, 960, 970, 980, 990]
  p y_vals = [-4.177412829697432, -4.1848393364765, -4.192296922237924, 
      -4.199785335389045, -4.207304330283102]
      
  fitting_svd(x_vals, y_vals, 4)

[950, 960, 970, 980, 990]
[-4.177412829697432, -4.1848393364765, -4.192296922237924, -4.199785335389045, -4.207304330283102]





Numo::DFloat#shape=[4]
[-3.65027, -0.000331299, -2.74726e-07, 4.14365e-11]

  vars = fitting_svd(x_vals, y_vals, 4)
  free_e_plot = lambda { |x| polynomials(vars, x) }

  pl = plot_data_and_func(x_vals, y_vals, free_e_plot)
  pl.show

./figs/fit_plot4.png

Mapleとの比較(overtaken?!)

得られた結果をMapleの結果と比較すると，

  f1 := x -> 7.526568118*x^3/10^9 + 
  (-1)*0.00002204463465*x^2 + 
  0.02077149587*x - 
  10.46814903

  f2:=unapply(-3.65027 
  -0.000331299*x 
  -2.74726e-07*x^2
  + 4.14365e-11*x^3, x);

  eV2J:=(1.60218*10**(-19))*(6.0221367*10**(23));
  subs(x=970,-x*diff(f1(x)*eV2J, x,x)); # by Maple fitting
  subs(x=970,-x*diff(f2(x)*eV2J, x,x)); # by Numo::svd
                        eV2J := 96485.46978
                            26.63998203
                            28.85328724

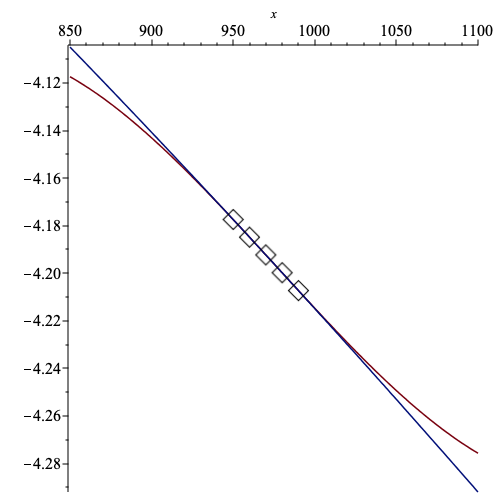
とズレがある．これをより広域のplotで比べると

./maple_figs/free_energy_fit_compare.png

Fitted free energy by SVD(blue) vs Maple(red).

うーーーん．見た目は Numo::Linalg.svdの勝ちだね．

実際，少しずれた温度(i.e. $T$=980) で$F(T)$を比べるとMapleは全然違う値．

エントロピー($S$)は $$Z = \left(\frac{\exp(-\Theta_E/2T)}{1-\exp(-\Theta_E/T)} \right)^{3N} \S = k_B \ln Z$$ だな．

Qiita記事作成のメモ

fit_plot.ipynbより途中で，qiita_org

  > qiita upload fit_plot.org

でfigsを登録したのちに，以下でQiita記事を作成．

  > jupyter nbconvert --to markdown fit_plot.ipynb
  > pandoc -f markdown -t org -o fit_plot.org fit_plot.md
  > rake fit_plot > tmp.org
  > qiita post tmp.org
  • source ~/current_research/higher_moment/moment_al/einstein/harmonic_free/tmp.org
1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?