背景

Pythonで体験するベイズ推論がMCMC(マルコフ連鎖モンテカルロ法)初心者の私にも分かりやすいうえに, 事例が豊富でかなりの良書だった. だけど, 株価のボラティリティ(分散)の計算が一部動かないのと, 主観的な推定だったものを, より客観的な推定にしてみたかったので, やってみた. また, 書籍ではpymc2だったけど, APIが豊富なpymc3を使った.

問題設定

2017年のAAPL, GOOG, TSLA, AMZNの株価(終値)を使って, 期待日次リターンをMCMCで推定する. また, 共分散行列を計算して, 株価の相関を求める.

環境設定

python3.6
numpy==1.13.3
pandas==0.22.0
matplotlib==2.1.1
pymc3==3.2
pandas_datareader==0.5.0

株価取得

pandas_datareaderを使って, Yahoo Financeから株価をもってくる.

import datetime
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pandas_datareader.data as web


start = datetime.datetime(2017, 1, 1)
end = datetime.datetime(2017, 12, 31)
aapl = web.DataReader("AAPL", 'yahoo', start, end)
goog = web.DataReader("GOOG", 'yahoo', start, end)
tsla = web.DataReader("TSLA", 'yahoo', start, end)
amzn = web.DataReader("AMZN", 'yahoo', start, end)

データ処理

今回使うのは終値だけ. それぞれの終値を別のDataFrameに格納する.

close = pd.concat([goog['Close'], aapl['Close'], tsla['Close'], amzn['Close']], axis=1)
close.columns = ['goog', 'aapl', 'tsla', 'amzn']
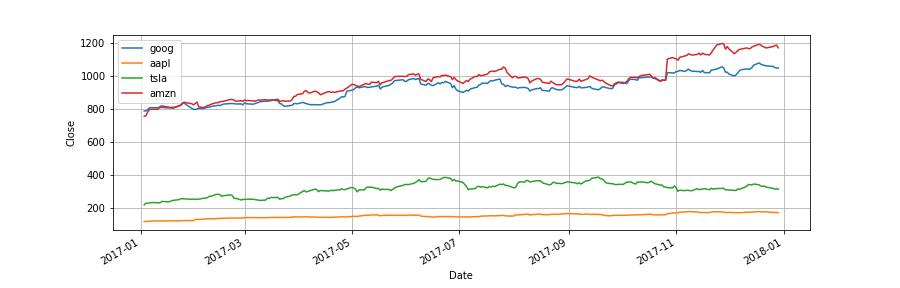
close.plot(grid=True)
plt.ylabel('Close')

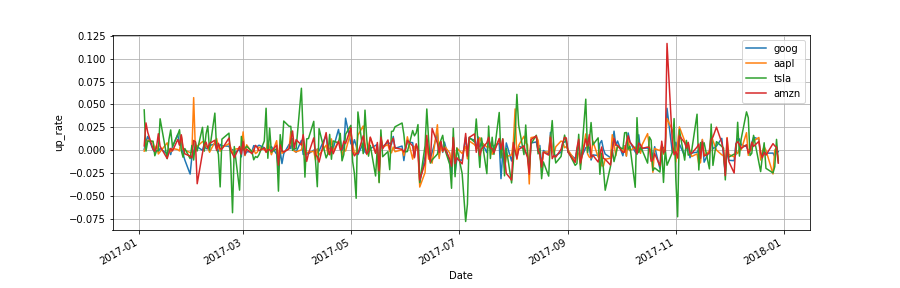
日次リターンを計算する.

up_rate = close.diff(axis=0) / close
up_rate.dropna(inplace=True)
up_rate.plot(grid=True)
plt.ylabel('up_rate')

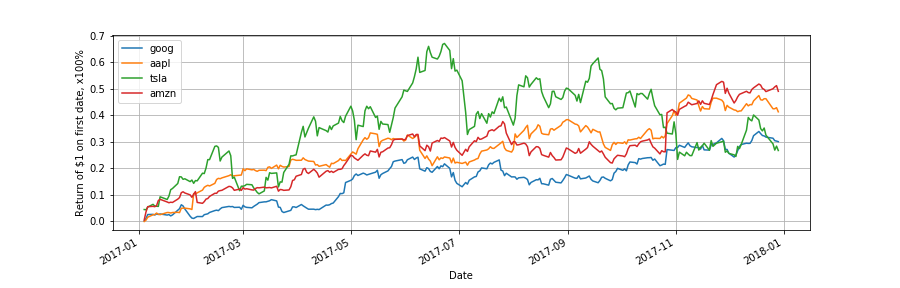
わかりにくいので, 初期投資1ドルに対するリターンをプロットする.

prod = (1 + up_rate).cumprod(axis=0) - 1
prod.plot(grid=True)
plt.ylabel('Return of $1 on first date, x100%')

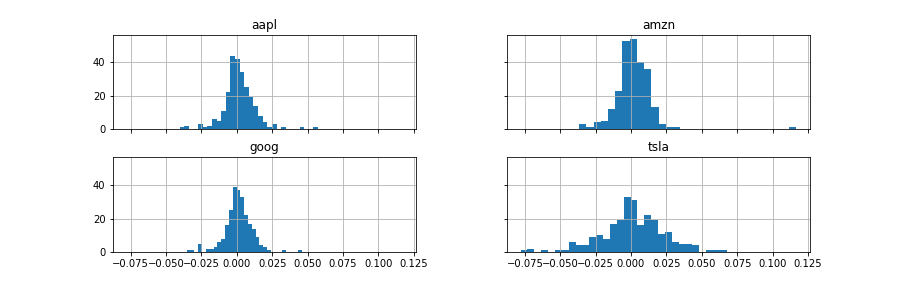
日次リターンのヒストグラム.

up_rate.hist(bins=30, sharex=True, sharey=True)

MCMCによる推定

いよいよ本題. MCMCについては書籍を見ていただきたい. 雑に説明すると, MCMCとは, 人工的に作り出したデータを利用して, ベイズの定理によって, 事後分布(今回の場合, 2017年の株価における期待日次リターンの分布)を得る手法である.

今回は, 期待日次リターンと株価のボラティリティを推定する. 書籍では, 決め打ちの事前分布を使っていたが, 株のプロではないので, もう少し客観的な事前分布を使いたい. そこで, 次のようにモデリングを行った.

期待日次リターンは正規分布とする.
$\mu$は一様分布から推定する.
$\sigma^2$はLKJ相関分布から推定する.

初めは, Wishert分布を使おうとしたが, Wishert分布の分散に一様分布などを使うと, LKJ相関分布を使えと怒られた.　LKJ相関分布については, pymc3のドキュメント内のこのページが分かりやすかった.

計算する

MCMCのパートは, 以下の通り.

import pymc3 as pm

with pm.Model() as model:
    # LKJCholeskyCovは下三角行列の要素をリストで返す
    packed_L = pm.LKJCholeskyCov("packed_L", n=4, eta=1., sd_dist=pm.HalfCauchy.dist(beta=2.5))
    # 下三角行列に変換する
    L = pm.expand_packed_triangular(4, packed_L, lower=True)
    # 共分散行列にする
    sigma = pm.Deterministic('sigma', L.dot(L.T))

    prior_mu = pm.Uniform("prior_mu", -1, 1, shape=4)
    mu= pm.Normal("returns", mu=prior_mu, sd=1, shape=4)

    obs = pm.MvNormal("observed_returns", mu=mu, chol=L, observed=up_rate)
    step = pm.NUTS()
    trace = pm.sample(50000, step)

NUTSを使っているので, pymc2より遅いかな.
NUTSについては, ドキュメントを見てください(あまり理解してない).

pymc3には強力な図化APIが用意されていて, 以下の通り.

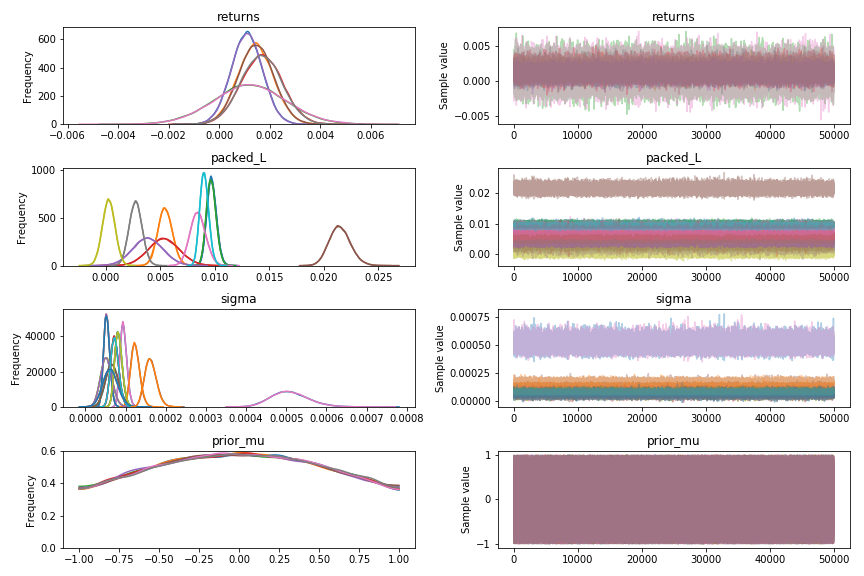
pm.traceplot(trace)

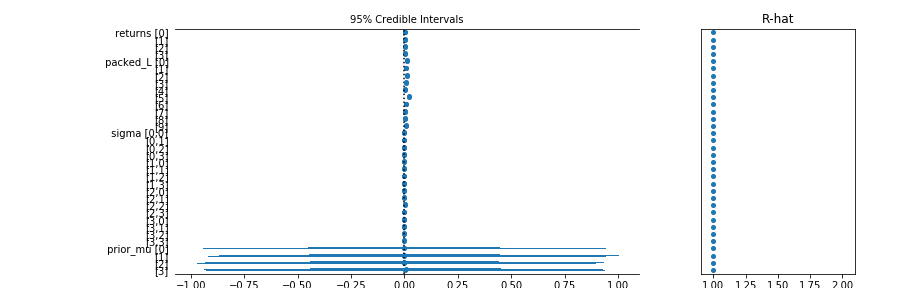
pm.forestplot(trace)

pymc3では$\hat{R}$も簡単に出してくれる. pymc2でも計算してみたが, pymc3のほうが収束がすごくいい. NUTSのおかげ.
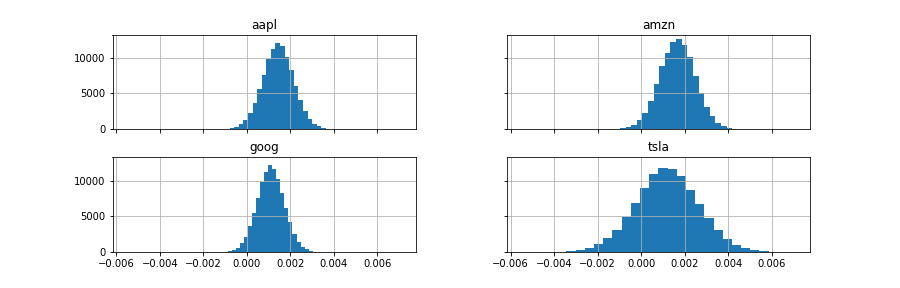
期待日次リターンの事後分布は以下のようになる.

mu_samples = pd.DataFrame(trace['returns'],
                          columns=['goog', 'aapl', 'tsla', 'amzn'])
mu_samples.hist(bins=30, sharex=True, sharey=True)

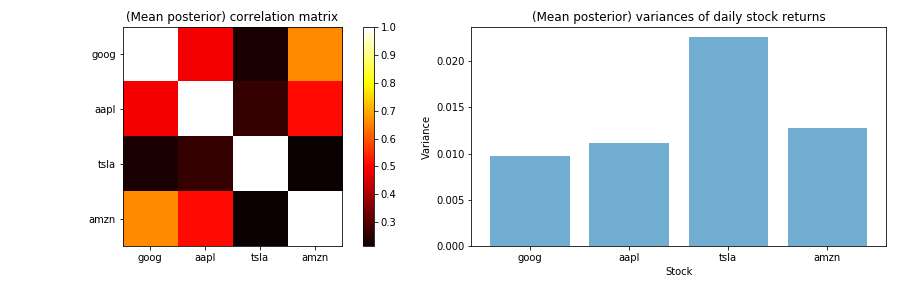
それぞれの株価の相関や分散は次のようになる.

sigma_post = trace["sigma"].mean(axis=0)

# 共分散行列から相関行列にする関数
def cov2corr(A):
    d = np.sqrt(A.diagonal())
    A = ((A.T / d).T) / d
    return A

plt.subplot(1, 2, 1)
plt.imshow(cov2corr(sigma_post), interpolation="none", cmap=plt.cm.hot)

plt.xticks(np.arange(4), up_rate.columns)
plt.yticks(np.arange(4), up_rate.columns)
plt.colorbar(orientation="vertical")
plt.title("(Mean posterior) correlation matrix")

plt.subplot(1, 2, 2)
plt.bar(np.arange(4), np.sqrt(np.diag(sigma_post)),
        color="#348ABD",
        alpha=0.7)
plt.xticks(np.arange(4), up_rate.columns)
plt.title("(Mean posterior) variances of daily stock returns")
plt.xlabel('Stock')
plt.ylabel('Variance')

plt.tight_layout()

GOOGとAMZNが相関が高いのは興味深い. どちらもクラウドやってるからかな.

まとめ

このぐらいだったら, 頻度主義に走って計算したほうが早い気がする(普通に相関行列を計算してもほぼ同じ). だけど, 真骨頂は損失関数を使ったベイズ点推定や, さらにモデルを複雑にした階層ベイズとからしい. 期待値とかが分布で出てくるのも, アバウト人間の私としては精神衛生上よろしい.

興味を持った方は, ぜひとも書籍を読んで欲しい. ダークマターのベイズ推定とかカッコイイ.

MCMC初心者がpymc3で株価の期待日次リターンを推定してみる

背景