Machine Learning Advent Calendarの20日目です。
はじめに
Naive Bayes(NB)とその改良版のTransformed Weight-normalized Complement Naive Bayes(TWCNB)、Averaged One-Dependence Estimators(AODE)という手法について解説と実装を書きます。
Naive Bayes
NBはベイズの定理と特徴変数間の独立性仮定を用いた分類器です。文書のカテゴリ分類等でよく利用されます。
NBは、事例$X$に対し$P(y|X)$が最大となるクラス$y$を分類結果として返します。$P(y|X)$は、ベイズの定理を用いて、以下のように展開が可能です。
P(y|X) = \frac{P(y, X)}{P(X)} = \frac{P(X|y)*P(y)}{P(X)} \propto P(X|y) * P(y)
また、$P(X|y)$は、特徴変数間の独立性仮定を用いて、以下のように展開が可能です。
P(X|y) = P(x_1, x_2, ..., x_n|y) = P(x_1|y)*P(x_2|y)*...*P(x_n|y)
これらから、分類結果yは
argmax P(y)\prod_{i=1}^nP(x_i|y)
で求めることができます。
実際には、$P(x_i|y)$の値は非常に小さく、それらを掛けあわせていくとアンダーフローを起こす可能性があるため、対数の和に変形して利用することが多いです。
argmax log(P(y)\prod_{i=1}^nP(x_i|y)) = argmax (logP(y) + \sum_{i=1}^nlogP(x_i|y))
学習データから、$P(y)$と$P(x_i|y)$の推定値を求めて、テストデータを分類する際に利用します。
NBは他の分類手法と比較すると、精度は劣ると言われているが、学習が高速なこと、実装が容易なことからよく用いられるようです。
# -*- coding: utf-8 -*-
import math
from collections import defaultdict
class NB(object):
"""
nb = NB()
training_data = [(1, {'a': 2, 'b': 2}), (2, {'a': 1, 'c': 4})]
nb.train(training_data)
testing_data = {'a': 1, 'b': 2}
result = nb.train(testing_data)
"""
def __init__(self):
"""
"""
self.all_categories = set()
self.category_word_count = defaultdict(lambda: defaultdict(int))
self.category_probability = defaultdict(float)
self.denominators = defaultdict(int)
def train(self, data):
"""dataを用いて分類器を学習する
"""
all_words = set()
category_count = defaultdict(int)
for category, document in data:
self.all_categories.add(category)
category_count[category] += 1
for word, count in document.iteritems():
all_words.add(word)
self.category_word_count[category][word] += count
for category in self.all_categories:
self.denominators[category] = sum(self.category_word_count[category].itervalues()) + len(all_words)
self.category_probability[category] = 1.0 * category_count[category] / len(data)
def classify(self, document):
"""documentが分類されるcategoryを返す
"""
scores = {category: self._calc_score(document, category)
for category in self.all_categories}
best = max(scores, key=scores.get)
return best
def _calc_score(self, document, category):
"""documentがcategoryに属するスコアを算出する
"""
score = math.log(self.category_probability[category])
for word, count in document.iteritems():
probability = self._calc_category_word_probability(word, category)
score += count * math.log(probability)
return score
def _calc_category_word_probability(self, word, category):
"""P(word|category)を算出する
"""
numerator = self.category_word_count[category][word] + 1.0
return 1.0 * numerator / self.denominators[category]
Transformed Weight-normalized Complement Naive Bayes
TWCNBは、NBの性能を悪化させている要因を解決するように、5つのヒューリスティクな改良を加えた分類器です。論文中では、TWCNBによってNBの実装の容易さと学習の高速さを保ったまま、SVMと同程度の性能に向上させることができたとあります。
1. Complement
カテゴリ間で学習データ数に偏りがあると、学習データ数が多いカテゴリを優先して選択しやすくなってしまうということがあります。カテゴリに属する確率を最大化するカテゴリを選択するのではなく、属さない確率を最小化するようなカテゴリを選択するように変更することによって、偏りの影響を緩和させます。($x_{ij}$はj番目の文書のi番目の単語の出現回数、$\alpha_{i}$はスムージング変数、$\alpha$はスムージング変数の和です。)
P(x_i|y) = \frac{\sum_{j:y_j = y}x_{ij} + \alpha_{i}}{\sum_{j:y_j = y}\sum_{k}x_{kj}+\alpha} => \frac{\sum_{j:y_j \ne y}x_{ij} + \alpha_{i}}{\sum_{j:y_j \ne y}\sum_{k}x_{kj}+\alpha}
2. Weight Normalization
実際には独立ではない特徴量間に独立性仮定を設ける事により、特徴量間に依存関係の強いクラスで、重みベクトルが大きくなってしまうことがあります。重みベクトルの値を正規化することによって、この影響を緩和させます。($w_{yi}$は$logP(x_i|y)$です。)
w_{yi} => \frac{w_{yi}}{\sum_iw_{yi}}
3. TF Transform
経験的に、単語の分布は多項モデルよりもロングテールな分布となります。単語の出現回数の対数を取ることによって、単語の分布をロングテールな分布に近づけます。
x_{ij} => log(x_{ij} + 1)
4. IDF Transform
頻出語はカテゴリ間での出現頻度や重みの差は小さいが、頻出するがゆえに、分類結果に大きく影響を与えてしまうことがあります。出現数にIDF値をかけることによって、頻出語の影響を緩和させます。($\delta_{ik}$は、文書kで単語iが出現すれば1、出現しなければ0をとる変数です。)
x_{ij} => x_{ij} * log(\frac{\sum_{k}1}{\sum_{k}\delta_{ik}})
5. Length Normalization
1度出現した単語は、独立性仮定に反して、同じ文書中に複数回出現することが多くなります。この影響を緩和するため、重みを文書長で正規化します。
x_{ij} => \frac{x_{ij}}{\sqrt{\sum_k(x_{kj})^2}}
以上の変更を加え、クラスの事前確率$P(y)$は、単語の事後確率$P(x_i|y)$に比べ、分類結果に不当に強い影響を与えてしまうことがあるため、省略します。結果として、分類結果yは、
argmin \sum_{i} x_i w_{yi}
で求まるようになります。
変更内容は容易であるが、数が多いため、NBよりもコードは大分長くなりました。
# -*- coding: utf-8 -*-
import math
from collections import defaultdict
from itertools import permutations, chain
class TWCNB(object):
"""
twcnb = TWCNB()
training_data = [(1, {'a': 2, 'b': 2}), (2, {'a': 1, 'c': 4})]
twcnb.train(training_data)
testing_data = {'a': 1, 'b': 2}
result = twcnb.train(testing_data)
"""
def __init__(self):
"""
"""
self.all_categories = set()
self.normalized_category_word_weight = defaultdict(lambda: defaultdict(int))
def train(self, data):
"""dataを用いて分類器を学習する
"""
category_word_count = self._calc_category_word_count(data)
all_words = set(chain.from_iterable(word_count.iterkeys() for word_count in category_word_count.itervalues()))
complement_category_word_count = self._calc_complement_category_word_count(category_word_count, all_words)
category_word_weight = self._calc_category_word_weight(complement_category_word_count, len(all_words))
normalized_category_word_weight = self._calc_normalized_category_word_weight(category_word_weight)
self.normalized_cat_word_weight = normalized_category_word_weight
def classify(self, document):
"""documentが分類されるcategoryを返す
"""
scores = {category: self._calc_score(document, category)
for category in self.all_categories}
best = min(scores, key=scores.get)
return best
def _calc_score(self, document, category):
"""documentがcategoryに属するスコアを算出する
"""
score = 0
for word, count in document.iteritems():
score += count * self.normalized_cat_word_weight[category][word]
return score
def _calc_idf(self, documents):
"""idf値を算出する
"""
df = defaultdict(int)
for document in documents:
for word in document.iterkeys():
df[word] += 1
idf = defaultdict(int)
document_count = len(documents)
for word, count in df.iteritems():
idf[word] = math.log(1.0 * document_count / count)
return idf
def _calc_category_word_count(self, data):
"""各カテゴリでの各単語の出現頻度を算出する
単語の出現頻度にはTF Transform, IDF Transform, Length Normalizationを行う
"""
documents = [d[1] for d in data]
idf = self._calc_idf(documents)
category_word_count = defaultdict(lambda: defaultdict(int))
for category, document in data:
tfidf_count = defaultdict(float)
for word, count in document.iteritems():
self.all_categories.add(category)
count = math.log(count + 1) # 3. TF Transform
count *= idf[word] # 4. IDF Transform
tfidf_count[word] = count
document_length = math.sqrt(sum(math.pow(v, 2) for v in tfidf_count.itervalues()))
for word, count in tfidf_count.iteritems():
count /= document_length # 5. Length Normalization
category_word_count[category][word] += count
return category_word_count
def _calc_complement_category_word_count(self, category_word_count, all_words):
"""あるカテゴリ以外(Comlement)のカテゴリでの各単語の出現頻度を算出する
"""
complement_category_word_count = defaultdict(lambda: defaultdict(int)) # 1. Complement
for word in all_words:
for category, other_category in permutations(self.all_categories, 2):
complement_category_word_count[category][word] += category_word_count[other_category][word]
return complement_category_word_count
def _calc_category_word_weight(self, complement_category_word_count, alpha):
"""各カテゴリでの各単語の重みを算出する
"""
category_word_weight = defaultdict(lambda: defaultdict(int))
for category, word_count in complement_category_word_count.iteritems():
theta_denominator = sum(word_count.itervalues()) + alpha
for word, count in word_count.iteritems():
theta = (count + 1) / theta_denominator
category_word_weight[category][word] = math.log(theta)
return category_word_weight
def _calc_normalized_category_word_weight(self, category_word_weight):
"""各カテゴリでの各単語の重みを正規化する(Weight Normalization)
"""
normalized_category_word_weight = defaultdict(lambda: defaultdict(int))
for category, word_weight in category_word_weight.iteritems():
weight_sum = sum(map(abs, word_weight.itervalues()))
for word, weight in word_weight.iteritems():
normalized_category_word_weight[category][word] = weight / weight_sum # 2. Weight Normalization
return normalized_category_word_weight
Averaged One-Dependence Estimators
NBの特徴変数間の独立性仮定を緩和した分類器です。
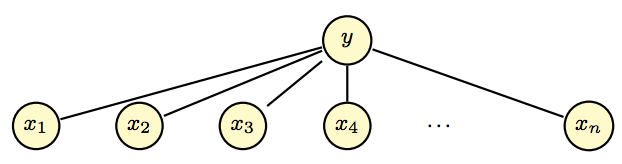
NBでは、各特徴量はクラスとのみ依存関係があり、特徴量間に依存関係はありませんでした。図にすると以下のようになります。
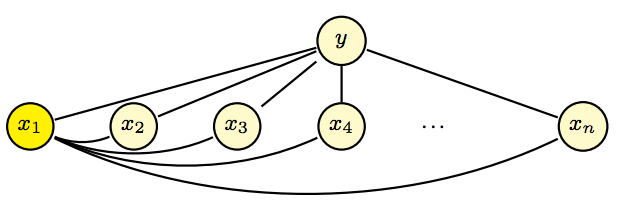
すべての特徴量を、クラスのみではなく、ある1つの特徴量(ペアレント)にも依存するように変更したモデルがOne-Dependence Estimatorsです。以下の図では、$x_1$がペアレントです。
P(y, X) = P(y, x_i)P(X|y, x_i)
argmax P(y, x_i)\prod_{j=1}^nP(x_j|y, x_i)
ODEはNBよりもバイアスは小さくなるが、バリアンスは大きくなる傾向があります。バリアンスが小さくなるように、ペアレントとなる特徴量を変更した複数のODEによる結果を平均したモデルが、Averaged One-Dependence Estimators(AODE)です。推定する確率が不正確なものにならないように、学習データにm回以上出現した特徴量のみをペアレントに用います。(論文中では、m=30を使用したとあります。)
P(y, X) = \frac{\sum_{i: |x_i| > m}P(y, x_i)P(X|y, x_i)}{|{i: |x_i| > m}|}
argmax \sum_{i: |x_i| > m}P(y, x_i)\prod_{j=1}^nP(x_j|y, x_i)
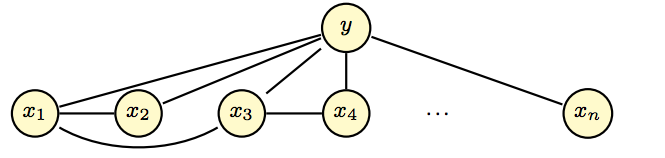
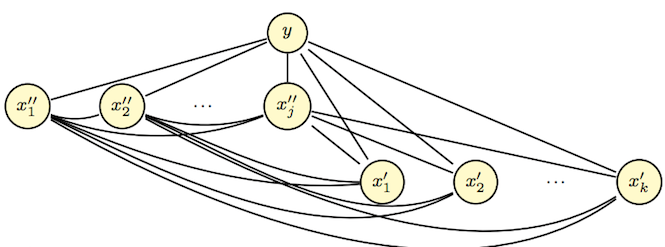
従来研究で、特徴変数間により複雑な依存関係を仮定したモデルはあったのですが、精度は良いが計算時間が掛かり過ぎるという欠点があり、それを解決するかたちでAODEが提案されたようです。(上がTANで、下がLRM)
# -*- coding: utf-8 -*-
from collections import defaultdict
from itertools import permutations
class AODE(object):
"""
aode = AODE()
training_data = [(1, {'a': 2, 'b': 2}), (2, {'a': 1, 'c': 4})]
aode.train(training_data)
testing_data = {'a': 1, 'b': 2}
result = aode.train(testing_data)
"""
def __init__(self, minimum_word_count=30):
"""
"""
self.minimum_word_count = minimum_word_count
self.all_categories = set()
self.word_count = defaultdict(int)
self.category_word_count = defaultdict(lambda: defaultdict(int))
self.category_word_pair_count = defaultdict(lambda: defaultdict(int))
def train(self, data):
"""dataを用いて分類器を学習する
"""
for category, document in data:
self.all_categories.add(category)
for word1, word2 in permutations(document.iterkeys(), 2):
self.word_count[word1] += 1
self.category_word_count[category][word1] += 1
self.category_word_pair_count[category][(word1, word2)] += 1
def classify(self, document):
"""documentが分類されるcategoryを返す
"""
scores = {category: self._calc_score(document, category)
for category in self.all_categories}
best = max(scores, key=scores.get)
return best
def _calc_score(self, document, category):
"""documentがcategoryに属するスコアを算出する
"""
score = 0.0
for word in document.iterkeys():
if self.word_count[word] < self.minimum_word_count:
# すべてm未満の時は、AODEではなく通常のNaive Bayesを用いるようにする等の処理が必要
continue
score += self._calc_one_dependence_score(document, category, word)
return score
def _calc_one_dependence_score(self, document, category, attribute):
"""attributeがペアレントの時に、documentがcategoryに属するスコアを算出する
P(category, attribute) * ΠP(word|category, attribute)
"""
score = (self.category_word_count[category][attribute] + 1.0) / len(self.word_count) + len(self.all_categories)
for word, count in document.iteritems():
score *= count * self._calc_one_dependence_probability(word, category, attribute)
return score
def _calc_one_dependence_probability(self, word, category, attribute):
"""P(word|category, attribute)
"""
numerator = self.category_word_pair_count[category][(word, attribute)] + 1.0
denominator = self.category_word_count[category][word] + len(self.word_count)
return 1.0 * numerator / denominator
実験
してないよ。比較したいね。
感想
いろいろあるもんだね。TWCNBは2003年で引用数371、AODEは2005年で引用数318になってます。最近だとどんなのがあるんだろう。
おわりに
おわりだよ。