はじめに
(注)
私は量子情報の専門家でも,情報の専門家でもありません。勉強している身です。不適切な表現あるいは誤り等ございましたらご指摘いただけると幸いです。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
今回は,以前IBM QのComposerで計算したものを,QISKitで改めて実装しました。
その備忘録としてメモ程度にまとめます。
実装
この記事では,以下のような演算になる量子回路を組むようにします。つまり,入力$\ket{b}$を上書きして出力$\ket{a+b}$を得る加算器のプログラムを作成します。
$$
\ket{a,b} \to \ket{a,a+b}
$$
詳細はIBM QのComposerで実装した記事の内容に譲ります。
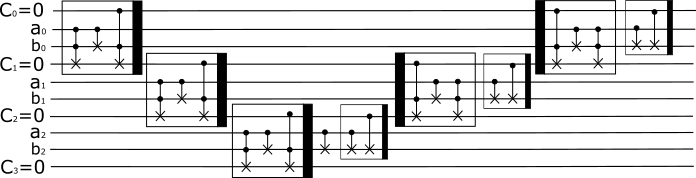
量子回路
QISKitで実装
上図のいくつかは使いまわせますので,carry,icarry,sumとしました。
def carry(circ, qr_1, qr_2, a, i):
circ.ccx(qr_1[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(a[i], qr_2[i], a[i+1])
def icarry(circ, qr_1, qr_2, a, i):
circ.ccx(a[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(qr_1[i], qr_2[i], a[i+1])
def sum(circ, ctl_1, ctl_2, tgt):
circ.cx(ctl_1, tgt)
circ.cx(ctl_2, tgt)
def adder(circ, a, b, c, n):
for i in range(n):
carry(circ, a, b, c, i)
circ.cx(a[n-1], b[n-1])
sum(circ, c[n-1], a[n-1], b[n-1])
for j in range(n-2, -1, -1):
icarry(circ, a, b, c, j)
sum(circ, c[j], a[j], b[j])
$a$と$b$をコマンドラインから入力できるように,最終的には次のように作ってみました。
とりあえず,量子ビット数も入力に合わせて変更されるようにしました。
import fire
from qiskit import QuantumCircuit, QuantumProgram
# Import basic plotting tools
from qiskit.tools.visualization import plot_histogram
def carry(circ, qr_1, qr_2, a, i):
circ.ccx(qr_1[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(a[i], qr_2[i], a[i+1])
def icarry(circ, qr_1, qr_2, a, i):
circ.ccx(a[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(qr_1[i], qr_2[i], a[i+1])
def sum(circ, ctl_1, ctl_2, tgt):
circ.cx(ctl_1, tgt)
circ.cx(ctl_2, tgt)
def adder(circ, a, b, c, n):
for i in range(n):
carry(circ, a, b, c, i)
circ.cx(a[n-1], b[n-1])
sum(circ, c[n-1], a[n-1], b[n-1])
for j in range(n-2, -1, -1):
icarry(circ, a, b, c, j)
sum(circ, c[j], a[j], b[j])
def plain_adder(a, b):
#--- 入力a, bをそれぞれ格納
input_1 = [a, int(len(bin(a)[2:]))]
input_2 = [b, int(len(bin(b)[2:]))]
print(input_1, input_2)
#--- 量子ビット数の決定
qb = max(input_1[1], input_2[1])
#--- 量子プログラムの開始
qp = QuantumProgram()
#--- localで使用するのでAPIの設定割愛
backend = 'local_qasm_simulator'
#--- レジスタの設定
aq = qp.create_quantum_register("aq", qb)
bq = qp.create_quantum_register("bq", qb)
cq = qp.create_quantum_register("cq", qb+1)
cc = qp.create_classical_register("cc", qb+1)
qcirc = qp.create_circuit("qcirc", [aq, bq, cq], [cc])
#--- 初期化
# 入力aを量子レジスタに反映
for i in range(input_1[1]):
if (1 << i) & input_1[0]:
qcirc.x(aq[i])
# 入力bを量子レジスタに反映
for i in range(input_2[1]):
if (1 << i) & input_2[0]:
qcirc.x(bq[i])
#--- Plain Adder
adder(qcirc, aq, bq, cq, qb)
#--- 測定
for i in range(qb):
qcirc.measure(bq[i], cc[i])
#--- オーバーフロー(桁上がり用)
qcirc.measure(cq[qb], cc[qb])
# Start Simulation
simulate = qp.execute(["qcirc"], backend=backend, shots=1, timeout=1800)
print(simulate.get_counts("qcirc"))
# ヒストグラム表示,今回は表示させません
plot_histogram(simulate.get_counts("qcirc"))
if __name__ == '__main__':
fire.Fire()
計算結果
たとえば,上のファイルをhoge.pyとして,20+21をしてみます。
計算結果は以下のようになり,ヒストグラムが表示されます。
$ python hoge.py plain_adder 20 21
[20, 5] [21, 5]
{'101001': 1}

おわりに
今回は,過去の記事で作成した加算器をQISKitを用いて実装してみました。
メモ程度ですが残していければと思います。
ここまで読んでくださってありがとうございました。
来歴
2018.01.30 新規作成