はじめに
(注)
私は量子情報の専門家でも,情報の専門家でもありません。勉強している身です。不適切な表現あるいは誤り等ございましたらご指摘いただけると幸いです。
前回に引き続き,モジュロ加算器についてもQISKitで実装しました。
その備忘録をメモ程度に残します。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
実装
具体的に作成したい回路は,次式を満たすものです。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
$$
\ket{a,b} \to \ket{a, a+b ,,\text{mod},, N} ,,,,(ただし,0 \leq a,b < N )
$$
この量子回路の実装は,$a+b$が$N$より大きいか小さいかに基づいています$(\because 0 \leq a+b < 2N)$。
測定後は,第2レジスタのみ結果のみ格納するようにします。
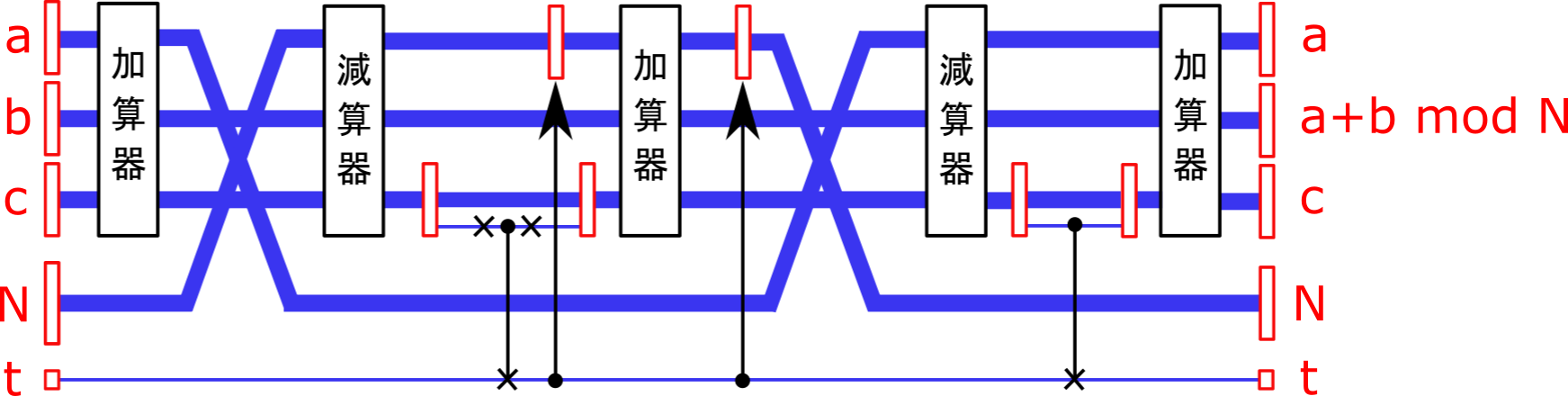
前回は,上図に基づいて実装しました。
矢印付きのゲートを実装する際に,$N$によって組み方が異なっておりましたが,余分にもう一つ$N$用のレジスタを用意することにより,量子回路全体が入力のみに依存するようにしました。
つまり,下記のように実装しました。$N=N_{spare}$です。
$$
\ket{a,b,c, N,N_{spare}, t} \to \ket{a, a+b ,,\text{mod},, N, c, N, N_{spare},t}
$$
QISKitで実装
加算器,減算器(adder,subtractor)は前回の内容をまとめて下記のようになります。
def carry(circ, qr_1, qr_2, a, i):
circ.ccx(qr_1[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(a[i], qr_2[i], a[i+1])
def icarry(circ, qr_1, qr_2, a, i):
circ.ccx(a[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(qr_1[i], qr_2[i], a[i+1])
def sum(circ, ctl_1, ctl_2, tgt):
circ.cx(ctl_1, tgt)
circ.cx(ctl_2, tgt)
def isum(circ, ctl_1, ctl_2, tgt):
# sum = isum
circ.cx(ctl_2, tgt)
circ.cx(ctl_1, tgt)
def adder(circ, a, b, c, n):
#--- |a>|b> -> |a>|a+b>
for i in range(n):
carry(circ, a, b, c, i)
circ.cx(a[n-1], b[n-1])
sum(circ, c[n-1], a[n-1], b[n-1])
for j in range(n-2, -1, -1):
icarry(circ, a, b, c, j)
sum(circ, c[j], a[j], b[j])
def subtractor(circ, a, b, c, n):
#--- |a>|b> -> |a>|a-b>
for i in range(n-1):
isum(circ, c[i], a[i], b[i])
carry(circ, a, b, c, i)
isum(circ, c[n-1], a[n-1], b[n-1])
circ.cx(a[n-1], b[n-1])
for j in range(n-1, -1, -1):
icarry(circ, a, b, c, j)
あとは,上の部品を組み合わせて完了です。最終的には次のようになりました。
import fire
from qiskit import QuantumCircuit, QuantumProgram
# Import basic plotting tools
from qiskit.tools.visualization import plot_histogram
def carry(circ, qr_1, qr_2, a, i):
circ.ccx(qr_1[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(a[i], qr_2[i], a[i+1])
def icarry(circ, qr_1, qr_2, a, i):
circ.ccx(a[i], qr_2[i], a[i+1])
circ.cx(qr_1[i], qr_2[i])
circ.ccx(qr_1[i], qr_2[i], a[i+1])
def sum(circ, ctl_1, ctl_2, tgt):
circ.cx(ctl_1, tgt)
circ.cx(ctl_2, tgt)
def isum(circ, ctl_1, ctl_2, tgt):
# sum = isum
circ.cx(ctl_2, tgt)
circ.cx(ctl_1, tgt)
def adder(circ, a, b, c, n):
#--- |a>|b> -> |a>|a+b>
for i in range(n):
carry(circ, a, b, c, i)
circ.cx(a[n-1], b[n-1])
sum(circ, c[n-1], a[n-1], b[n-1])
for j in range(n-2, -1, -1):
icarry(circ, a, b, c, j)
sum(circ, c[j], a[j], b[j])
def subtractor(circ, a, b, c, n):
#--- |a>|b> -> |a>|a-b>
for i in range(n-1):
isum(circ, c[i], a[i], b[i])
carry(circ, a, b, c, i)
isum(circ, c[n-1], a[n-1], b[n-1])
circ.cx(a[n-1], b[n-1])
for j in range(n-1, -1, -1):
icarry(circ, a, b, c, j)
def modulo_adder(a, b, N):
# 入力a, bをそれぞれinputに格納
input_1 = [a, int(len(bin(a)[2:]))]
input_2 = [b, int(len(bin(b)[2:]))]
input_3 = [N, int(len(bin(N)[2:]))]
print(input_1, input_2, input_3)
#--- 量子ビット数
qb = max(input_1[1], input_2[1], input_3[1])
#--- 量子プログラムの開始
qp = QuantumProgram()
#--- localで使用するのでAPIの設定割愛
backend = 'local_qasm_simulator'
#--- レジスタの設定
aq = qp.create_quantum_register("aq", qb)
bq = qp.create_quantum_register("bq", qb)
cq = qp.create_quantum_register("cq", qb+1)
nq = qp.create_quantum_register("nq", qb)
nq_spare = qp.create_quantum_register("nq_spare", qb)
tq = qp.create_quantum_register("tq", 1)
cc = qp.create_classical_register("cc", qb+1)
qcirc = qp.create_circuit("qcirc", [aq, bq, cq, nq, nq_spare, tq], [cc])
#--------------
#--- 初期化
#--------------
# 入力aを反映
for i in range(input_1[1]):
if (1 << i) & input_1[0]:
qcirc.x(aq[i])
# 入力bを反映
for i in range(input_2[1]):
if (1 << i) & input_2[0]:
qcirc.x(bq[i])
# 入力Nを反映
for i in range(input_3[1]):
if (1 << i) & input_3[0]:
qcirc.x(nq[i])
qcirc.x(nq_spare[i])
#--------------
#--- 演算
#--------------
#--- Adder
adder(qcirc, aq, bq, cq, qb)
#--- Swap (a, N)
for i in range(qb):
qcirc.swap(aq[i], nq[i])
#--- Substractor
subtractor(qcirc, aq, bq, cq, qb)
#--- Overflow
qcirc.x(cq[qb])
qcirc.cx(cq[qb], tq[0])
qcirc.x(cq[qb])
#--- Arrow Gate
for i in range(input_3[1]):
if (1 << i) & input_3[0]:
qcirc.ccx(tq[0], nq_spare[i], aq[i])
#--- Adder (result in modulo adder)
adder(qcirc, aq, bq, cq, qb)
#--------------
#--- 後処理
#--------------
# Arrow
for i in range(input_3[1]):
if (1 << i) & input_3[0]:
qcirc.ccx(tq[0], nq_spare[i], aq[i])
# Swap (a, N)
for i in range(qb):
qcirc.swap(aq[i], nq[i])
# Subtractor
subtractor(qcirc, aq, bq, cq, qb)
# Reset tq
qcirc.cx(cq[qb], tq[0])
# Adder
adder(qcirc, aq, bq, cq, qb)
#--- Measure
for i in range(qb):
qcirc.measure(bq[i], cc[i])
#--- Overflow
qcirc.measure(cq[qb], cc[qb])
# Start Simulation
simulate = qp.execute(["qcirc"], backend=backend, shots=1, timeout=1800)
print(simulate.get_counts("qcirc"))
# Histogram
plot_histogram(simulate.get_counts("qcirc"))
if __name__ == '__main__':
fire.Fire()
上のファイルをhoge.pyとして,例えば 4 + 6 mod 7は次のように計算できます。
$N$が4量子ビット以上になると,ローカルで計算する場合かなりの時間とメモリを要するため,
3量子ビットとしました。
$ python hoge.py modulo_adder 4 6 7
[4, 3] [6, 3] [7, 3]
{'0011': 1}
おわりに
今回は過去記事で作成したモジュロ加算器をQISKitを用いて実装しました。
計算時間を要すると推察されますが,制御モジュロ乗算器も時間があるときにできればいいなと思います。
来歴
2018.01.31 新規作成