量子コンピュータ（シミュレータ）でモジュロ加算器を作る

はじめに

（注）
私は量子情報の専門家でも，情報の専門家でもありません。勉強している身です。不適切な表現あるいは誤り等ございましたらご指摘いただけると幸いです。

前回の記事ではIBM Qを用いてモジュール化可能な加算器を作成してみました。

今回の記事では，モジュロ演算の中でも比較的容易に量子回路を作成できる加算（以降，モジュロ加算と呼ぶ）に焦点を当てて作成したいと思います。今回も備忘録として残します。

具体的に作成したい回路は，次式を満たすものです。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

$$
\ket{a,b} \to \ket{a, a+b ,,\text{mod},, N}　,,,,(ただし，0 \leq a,b < N )
$$
この量子回路の実装は，$a+b$が$N$より大きいか小さいかに基づいています$(\because 0 \leq a+b < 2N)$。
前回，オーバーフロー用のビットを用いて，数の比較ができることを少し書きました。今回はそれが活躍することになります。

また，今回も具体的な回路を示すため，前回同様3量子ビットのモジュロ加算の量子回路を作るものとします。
したがって，$0 \leq a+b < 7$の範囲で有効な回路となります。

IBM Q：加算器・減算器・SWAPゲートのサブルーチン化

前回の記事では具体的なモジュール（サブルーチン）化する方法に触れませんでしたので，まずここで実装します。
おさらいになりますが加算器・減算器，そして後ほど使用するSWAPゲートを以下に示します。

• 加算器
  

• 減算器（可逆であることを利用して，加算器を反転）
  

• SWAPゲート
  （a[0], b[0], c[0]）と（d[0], e[0], f[0]）を入れ替えます。
  

サブルーチンの追加

IBM QではAdd subroutineからサブルーチンを定義しゲートとして追加することが可能です。

上記の3つ演算をサブルーチンとして追加します。

• 加算器

gate add3 a,b,c,d,e,f,g,h,i,j {
    // |a>|b> → |a>|b+a>
    // a:(a0, a1, a2) = (a, b, c)
    // b:(b0, b1, b2) = (d, e, f)
    // c:(c0, c1, c2) = (g, h, i)
    // c3 = j for overflow
    ccx a,d,h;
    cx a,d;
    ccx g,d,h;
    ccx b,e,i;
    cx b,e;
    ccx h,e,i;
    ccx c,f,j;
    cx c,f;
    ccx i, f,j;
    cx c,f;
    cx c,f;
    cx i,f;
    ccx h,e,i;
    cx b,e;
    ccx b,e,i;
    cx b,e;
    cx h,e;
    ccx g,d,h;
    cx a,d;
    ccx a,d,h;
    cx a,d;
    cx g,d;
}

• 減算器

gate sub3 a,b,c,d,e,f,g,h,i,j {
    // |a>|b> → |a>|b-a>
    // a:(a0, a1, a2) = (a, b, c)
    // b:(b0, b1, b2) = (d, e, f)
    // c:(c0, c1, c2) = (g, h, i)
    // c3 = j for overflow
    cx g,d;
    cx a,d;
    ccx a,d,h;
    cx a,d;
    ccx g,d,h;
    cx h,e;
    cx b,e;
    ccx b,e,i;
    cx b,e;
    ccx h,e,i;
    cx i,f;
    cx c,f;
    cx c,f;
    ccx i,f,j;
    cx c,f;
    ccx c,f,j;
    ccx h,e,i;
    cx b,e;
    ccx b,e,i;
    ccx g,d,h;
    cx a,d;
    ccx a,d,h;
}

• SWAPゲート

gate swap3 a,b,c,d,e,f {
    // SWAP between (a,b,c) and (d,e,f)
    cx a,d;
    cx d,a;
    cx a,d;
    cx b,e;
    cx e,b;
    cx b,e;
    cx c,f;
    cx f,c;
    cx c,f;
}

上記を実装すると，以下のように新たにゲートが表示されるようになります。

さて，これでついに3量子ビットの加算器・減算器・SWAPゲートのサブルーチンが完成しました。
これにより，作成に何列も必要だった量子回路が，たった一列で作成できることになります。

IBM Q：モジュロ加算器の実装

準備も完了したので，モジュロ加算器の作成に取り掛かりたいと思います。
もう一度，式を記載します。
$$
\ket{a,b} \to \ket{a, a+b ,,\text{mod},, N}　,,,,(ただし，0 \leq a,b < N )
$$
参考文献と同様に実装します。IBM Q上では下記のようになります。
具体的な例を挙げるために$N={3, 4, 5, 6, 7}$のときを示します。

• $N=3$
  

• $N=4$
  

• $N=5$
  

• $N=6$
  

• $N=7$
  

上記の赤枠点線部分は，$N$によって回路を変える必要がありました。
ここを$N$の値によらず組む方法を思いつきませんでした。もしご存知な方がいらっしゃれば，ぜひ教えていただきたいです。

IBM Q：検算

上述した量子回路を利用して，$a+b ,,\text{mod},, N,,,(0 \leq a,b < N)$を計算できることは確認しておりますが，いくつか計算例を示したいと思います。計算結果中，赤枠で囲っていない量子ビットは前回の記事で説明しましたのであえて囲いませんでした。

• $(2+1) ,,\text{mod},, 3 = 000_2 = 0$
  

• $(3+3) ,,\text{mod},, 4 = 010_2 = 2$
  

• $(3+4) ,,\text{mod},, 6 = 001_2 = 1$
  

• $(2+3) ,,\text{mod},, 7 = 101_2 = 5$
  

モジュロ加算器の仕組み

なぜ，上述した量子回路でうまく計算できるのでしょうか？
以降は，簡単に上の説明をしたいと思います。

全体の流れ

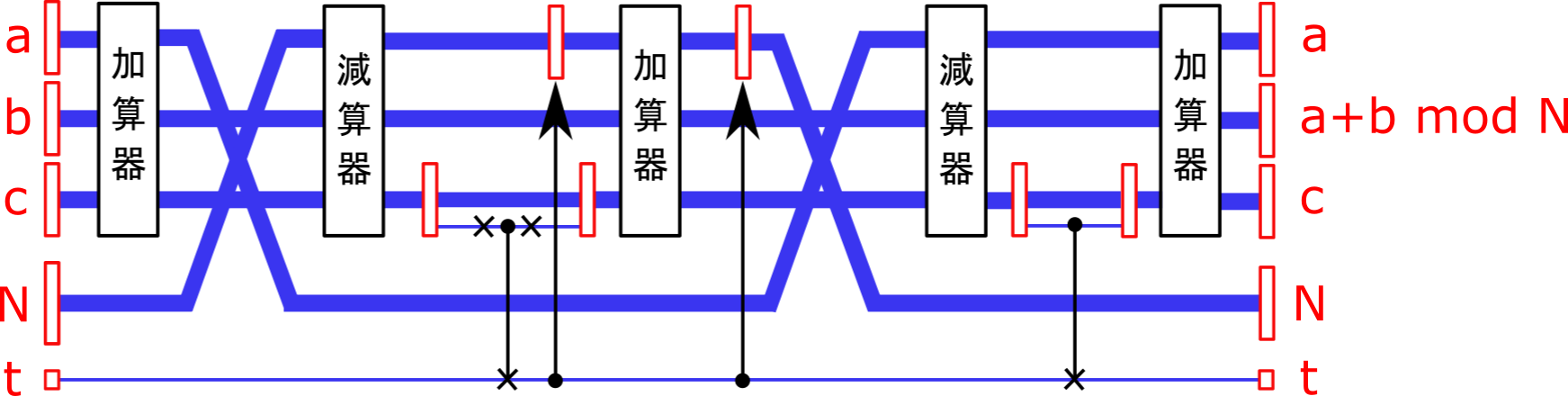
モジュロ加算器のイメージ図は次のようになります。
ここでは便宜上，上$(a)$から下$(t)$まで第1～第5レジスタと呼ぶようにします。
なお，$a$，$b$，$N$は3量子ビット，$c$は4量子ビット，$t$は1量子ビットとし，$0 \leq a, , ,b < N$であることをもう一度書き留めておきます。

加算結果を格納する第2レジスタと，法となる数$N$を3量子ビットとしていますので，加算によってオーバーフローしないような入力$a$，$b$を考えます。つまり，$0 \leq a+b < 7,$です（$N$は$a,b < N \leq 7$）。オーバーフロー用の$c$の最上位のビットは"0"としておきます。

入力・出力はそれぞれ左端，右端に記載しました。加算器・減算器は前回の記事で説明した通りですね。
×印単体はNOTゲートです。矢印付きのゲートは後ほど説明します。

もう少し細かく見ていきます。

1) 加算およびSWAP

上記，点線枠の処理は初期状態を$\ket{a}\ket{b}\ket{c}\ket{N}\ket{t}=\ket{a}\ket{b}\ket{c}\ket{N}\ket{0}$とすると，次のようになります。
$$
\ket{a}\ket{b}\ket{c}\ket{N}\ket{0} \to \ket{a}\ket{a+b}\ket{c}\ket{N}\ket{0}
\to \ket{N}\ket{a+b}\ket{c}\ket{a}\ket{0}
$$
まず初めに加算し，そのあと第1レジスタと第4レジスタをSWAPゲートで入れ替えました。
いま，第2レジスタ$\ket{b}$を3量子ビットとして入力を設定していますから，$a+b$はこの時点でオーバーフローすることはありません。

2) 減算およびモジュロ加算の前計算

まずは，減算です。以下のようになります。
$$
\ket{N}\ket{a+b}\ket{c}\ket{a}\ket{0}
\to
\ket{N}\ket{a+b-N}\ket{c'}\ket{a}\ket{0}
$$
この減算によって，結果は2パターンあります。そのまえに，矢印付きのゲートについて説明します。これは以下の演算をするものです。つまり，第5レジスタが$\ket{1}$のとき，第1レジスタを$\ket{0}$にして，そうでないときは何もしない処理です。

  \begin{cases}
     \ket{N} \to \ket{N} &  \text{if} \ket{t} = \ket{0} \\
     \ket{N} \to \ket{0} &  \text{if} \ket{t} = \ket{1} &
  \end{cases}

$N$が既知でありますから，可逆ゲートを実現するためには，制御NOTゲートを利用すればいいことがわかります($N$を二進数表記し，"1"である量子ビットをすべて制御NOTゲートの目標ビットとする；制御ビットは第5レジスタ)。

• $a+b-N < 0$のとき：

$c'$の最上位ビット，すなわち，オーバーフロー用のフラグが立ちます。つまり，$\ket{c'}=\ket{1 c_2 c_1 c_0}$です。少し汚い書き方ですが，第3・5レジスタが2進数表記であることに注意して，そのあとの処理は次のようになります。
$$
\ket{N}\ket{a+b-N}\ket{1 c_2 c_1 c_0}\ket{a}\ket{0}
\to
\ket{N}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{0}
\to
\ket{N}\ket{a+b-N}\ket{1 c_2 c_1 c_0}\ket{a}\ket{0}
$$

• $a+b-N \geq 0$のとき：

$\ket{c'}=\ket{0 c_2 c_1 c_0}$です。第3・5レジスタが2進数表記であることに注意して，そのあとの処理は次のようになります。
$$
\ket{N}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{0}
\to
\ket{N}\ket{a+b-N}\ket{1 c_2 c_1 c_0}\ket{a}\ket{0}
\to
\ket{0}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{1}
$$

3) モジュロ加算および後処理の前計算

• $a+b-N < 0$のとき：

まず，加算です。この計算結果がモジュロ加算の計算結果として第2レジスタに格納されることとなります。$N$を足すことにより負の数から正の数に桁上がりするので，オーバーフロー用のビットが反転します。

$$
\ket{N}\ket{a+b-N}\ket{1 c_2 c_1 c_0}\ket{a}\ket{0}
\to
\ket{N}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{a}\ket{0}
$$

そして，2つ目の矢印付きゲートの処理です。
2)で説明したように1つ目の矢印付きゲートでは，$\ket{N}$を2進数表記したときの"1"のビットを制御ゲート，$\ket{t}$を目標ゲートとした制御NOTゲートが配置されています。この計算を逆に実行するために，1つ目の矢印付きゲートを反転させたものを配置します。したがって，2つ目の矢印付きゲートは，第1レジスタに対して，下記の処理をすることになります。

  \begin{cases}
     \ket{N} \to \ket{N} &  \text{if} \ket{t} = \ket{0} \\
     \ket{0} \to \ket{N} &  \text{if} \ket{t} = \ket{1} &
  \end{cases}

つまり$a+b-N < 0$のときは$\ket{t}=\ket{0}$ですから何もしません。SWAPゲートの処理も考慮して，次のように計算されます。

$$
\ket{N}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{a}\ket{0}
\to
\ket{a}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0}
$$

[](さて，この時点の第2ビットは$a+b$ですが，いま$a+b-N<0$ですから，$a+b<N$が成り立っています。
つまり，$a+b = a+b,,\text{mod},,N$が成り立ち，以下のように書き直せます。)

[]($$
\ket{a}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} =
\ket{a}\ket{a+b,,\text{mod},,N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0}
$$)

• $a+b-N \geq 0$のとき：

まず，加算です。第1レジスタが$\ket{0}$なので，何もしないことになりますね。

$$
\ket{0}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{1}
\to
\ket{0}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{1}
$$

矢印付きゲートの処理に注意すると，下記のように計算できます。

$$
\ket{0}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{1}
\to
\ket{N}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{a}\ket{1}
\to
\ket{a}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{1}
$$

[](このとき，$0 \leq a,b < N$より$0 \leq a+b < 2N$なので，$0 \leq a+b-N < N$です。
したがって，$a+b-N=a+b,,\text{mod},,N$，以下のように書き直せます。)

[]($$
\ket{a}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{1} =
\ket{a}\ket{a+b,,\text{mod},,N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{1}
$$)

4) 後処理

1)～3)までの計算で，欲しかった計算処理は第2レジスタに格納されています。後処理とは，第5レジスタを初期化すること（$\ket{t}=\ket{0}$の状態にすること）です。

• $a+b-N < 0$のとき：

まずは，減算です。第2レジスタから$a$が引かれます。$(a+b)-a>0$ですから，オーバーフロー用のレジスタは反転しないため，第5レジスタの量子ビットは反転しません。最後，再び$a$が第2レジスタに加算されます。一連の処理は次のようになります。

$$
\ket{a}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} \to
\ket{a}\ket{(a+b)-a}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} \to
\ket{a}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0}
$$

さて，この時点の第2レジスタは$a+b$ですが，いま$a+b-N<0$ですから，$a+b<N$が成り立っています。
つまり，$a+b = a+b,,\text{mod},,N$が成り立ち，以下のように書き直せます。

$$
\ket{a}\ket{a+b}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} =
\ket{a}\ket{a+b,,\text{mod},,N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} =
\underline{\underline{\ket{a}\ket{a+b,,\text{mod},,N}\ket{c}\ket{N}\ket{t}}}
$$

• $a+b-N \geq 0$のとき：

まずは，減算です。第2レジスタから$a$が引かれます。$(a+b-N)-a<0$ですから，オーバーフロー用のレジスタは反転し，第5レジスタの量子ビットもまた制御NOTゲートにより反転します。最後，再び$a$が第2レジスタに加算されます。一連の処理は次のようになります。

\begin{align}
\ket{a}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{1}
\to
&\ket{a}\ket{(a+b-N)-a}\ket{1 c_2 c_1 c_0}\ket{N}\ket{1} \\ \\
\to
&\ket{a}\ket{(a+b-N)-a}\ket{1 c_2 c_1 c_0}\ket{N}\ket{0} \\ \\
\to 
&\ket{a}\ket{(a+b-N)-a}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} \\ \\
\to
&\ket{a}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{0} 
\end{align}

このとき，$0 \leq a,b < N$より$0 \leq a+b < 2N$なので，$0 \leq a+b-N < N$です。
したがって，$a+b-N=a+b,,\text{mod},,N$が成り立ち，以下のように書き直せます。

$$
\ket{a}\ket{a+b-N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{1} =
\ket{a}\ket{a+b,,\text{mod},,N}\ket{0 c_2 c_1 c_0}\ket{N}\ket{1} =
\underline{\underline{\ket{a}\ket{a+b,,\text{mod},,N}\ket{c}\ket{N}\ket{t}}}
$$

以上が，モジュロ加算器の仕組みになります。

おわりに

今回の記事では，以下のことを備忘録として書かせていただきました。

• 加算器・減算器のサブルーチン（モジュール）化

• モジュロ加算器の作成

• モジュロ加算器の仕組み

次回は，モジュロ乗算器について書ければいいなと考えています。
モジュロ乗算器はこのモジュロ加算器をさらにモジュール化して作成することになりそうです。
（結構難しそうなので，次回までは時間があくと思います）

思ったより長くなってしまいました。
ここまで読んでいただきありがとうございました。

参考文献

Vlatko Vedral, Adriano Barenco and Artur Ekert, "Quantum Networks for Elementary Arithmetic Operations"