$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
前回の記事で量子コンピュータを少し試しました。
IBM Qは,これから量子計算を勉強するにあたり,とても良い教材だと感じています。
今回は,4量子ビットの量子フーリエ変換に挑戦したいと思います
(厳密な定義等は,専門書を参照ください)。
量子フーリエ変換
離散フーリエ変換の入力に量子状態のベクトルを使用することで,量子フーリエ変換を実行できます。正規直交基底ベクトル $\ket{0},\ket{1},\ket{2},...\ket{i},...\ket{j},...\ket{N-1}$に対して,$N=2^n$のとき,次のように定義されます。
U_{QFT}\ket{x}=\frac{1}{\sqrt{N}}\sum_{y=0}^{N-1}e^{\frac{2\pi i}{N}xy}\ket{y}
=\frac{1}{\sqrt{N}}\sum_{y=0}^{N-1}\omega^{xy}\ket{y}
量子フーリエ変換のユニタリ行列は次のようになります。
QFT_N = \frac{1}{\sqrt{N}}
\left(
\begin{array}{cccc}
1 & 1 & \cdots & 1 \\
1 & \omega & \cdots & \omega^{N-1} \\
\vdots & \vdots & & \vdots \\
1 & \omega^{N-1} & \cdots & \omega^{(N-1)(N-1)}
\end{array}
\right)
例えば,一般に$N=2^n$のとき,$\ket{0}$($n$ ビット)を量子フーリエ変換すると次のようになります。つまり,等確率で観測される重ね合わせ状態ができます。なお,$\omega=e^{\frac{2\pi i}{N}}$です。
U_{QFT}\ket{0} = \frac{1}{\sqrt{N}}
\left(
\begin{array}{cccc}
1 & 1 & \cdots & 1 \\
1 & \omega & \cdots & \omega^{N-1} \\
\vdots & \vdots & & \vdots \\
1 & \omega^{N-1} & \cdots & \omega^{(N-1)(N-1)}
\end{array}
\right)
\left(\begin{array}{c}
1 \\
0 \\
\vdots \\
0
\end{array}
\right)
= \frac{1}{\sqrt{N}}
\left(\begin{array}{c}
1 \\
1 \\
\vdots \\
1
\end{array}
\right)
= \frac{1}{\sqrt{N}}
\left[
\ket{0}+\ket{1}+\ket{2}+\cdots+\ket{N-1}
\right]
量子フーリエ変換のユニタリ行列
上述したユニタリ行列を備忘録として,具体的に1量子ビット〜4量子ビットの場合で書きたいと思います。
1量子ビット(N=2)の場合
$\omega=e^{\frac{2\pi i}{2}}=e^{\pi i}=-1$です。よって,アダマール変換と一致します。
QFT_{N=2}=
\frac{1}{\sqrt{2}}
\left(\begin{array}{cc}
1 & 1 \\
1 & \omega^1 \\
\end{array}
\right)=
\frac{1}{\sqrt{2}}
\left(\begin{array}{cc}
1 & 1 \\
1 & -1 \\
\end{array}
\right)
= H
2量子ビット(N=4)の場合
$\omega=e^{\frac{2\pi i}{4}}=e^{\frac{\pi i}{2}}=i$です。
QFT_{N=4}=
\frac{1}{\sqrt{4}}
\left(\begin{array}{cccc}
1 & 1 & 1 & 1\\
1 & \omega^1 & \omega^2 & \omega^3 \\
1 & \omega^2 & \omega^4 & \omega^6 \\
1 & \omega^3 & \omega^6 & \omega^9
\end{array}
\right)=
\frac{1}{\sqrt{4}}
\left(\begin{array}{cccc}
1 & 1 & 1 & 1 \\
1 & i & -1 & i \\
1 & -1 & 1 & -1 \\
1 & -i & -1 & i
\end{array}
\right)
3量子ビット(N=8)の場合
$\omega=e^{\frac{2\pi i}{8}}=e^{\frac{\pi i}{4}}=\frac{1+i}{\sqrt{2}}$です。$\omega^0=\omega^8=\cdots$となること等を利用すると,ユニタリ行列は次のようになります。
QFT_{N=8}=
\frac{1}{\sqrt{8}}
\left(\begin{array}{cccccccc}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & \omega^1 & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6 & \omega^7 \\
1 & \omega^2 & \omega^4 & \omega^6 & 1 & \omega^2 & \omega^4 & \omega^6 \\
1 & \omega^3 & \omega^6 & \omega^1 & \omega^4 & \omega^7 & \omega^2 & \omega^5 \\
1 & \omega^4 & 1 & \omega^4 & 1 & \omega^4 & 1 & \omega^4 \\
1 & \omega^5 & \omega^2 & \omega^7 & \omega^4 & \omega^1 & \omega^6 & \omega^3 \\
1 & \omega^6 & \omega^4 & \omega^2 & 1 & \omega^6 & \omega^4 & \omega^2 \\
1 & \omega^7 & \omega^6 & \omega^5 & \omega^4 & \omega^3 & \omega^2 & \omega^1
\end{array}
\right)
4量子ビット(N=16)の場合
$\omega=e^{\frac{2\pi i}{16}}=e^{\frac{\pi i}{8}}$です。$\omega^0=\omega^{16}=\cdots$となること等を利用すると,ユニタリ行列は次のようになります。
QFT_{N=16}=
\frac{1}{\sqrt{16}}
\left(\begin{array}{cccccccccccccccc}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & \omega^1 & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6 & \omega^7 & \omega^8 & \omega^9 & \omega^{10} & \omega^{11} & \omega^{12} & \omega^{13} & \omega^{14} & \omega^{15} \\
1 & \omega^2 & \omega^4 & \omega^6 & \omega^8 & \omega^{10} & \omega^{12} & \omega^{14} & 1 & \omega^2 & \omega^4 & \omega^6 & \omega^8 & \omega^{10} & \omega^{12} & \omega^{14} \\
1 & \omega^3 & \omega^6 & \omega^9 & \omega^{12} & \omega^{15} & \omega^3 & \omega^6 & \omega^9 & \omega^{12} & \omega^{15} & \omega^3 & \omega^6 & \omega^9 & \omega^{12} & \omega^{15} \\
1 & \omega^4 & \omega^8 & \omega^{12} & 1 & \omega^4 & \omega^8 & \omega^{12} & 1 & \omega^4 & \omega^8 & \omega^{12} & 1 & \omega^4 & \omega^8 & \omega^{12} \\
1 & \omega^5 & \omega^{10} & \omega^{15} & \omega^5 & \omega^{10} & \omega^{15} & \omega^5 & \omega^{10} & \omega^{15} & \omega^5 & \omega^{10} & \omega^{15} & \omega^5 & \omega^{10} & \omega^{15} \\
1 & \omega^6 & \omega^{12} & \omega^3 & \omega^9 & \omega^{15} & \omega^6 & \omega^{12} & \omega^3 & \omega^9 & \omega^{15} & \omega^6 & \omega^{12} & \omega^3 & \omega^9 & \omega^{15} \\
1 & \omega^7 & \omega^{14} & \omega^6 & \omega^{13} & \omega^5 & \omega^{12} & \omega^4 & \omega^{11} & \omega^3 & \omega^{10} & \omega^2 & \omega^9 & \omega^1 & \omega^8 & \omega^{15} \\
1 & \omega^8 & \omega^1 & \omega^9 & \omega^2 & \omega^{10} & \omega^3 & \omega^{11} & \omega^4 & \omega^{12} & \omega^5 & \omega^{13} & \omega^6 & \omega^{14} & \omega^7 & \omega^{15} \\
1 & \omega^9 & \omega^3 & \omega^{12} & \omega^6 & \omega^{15} & \omega^9 & \omega^3 & \omega^{12} & \omega^6 & \omega^{15} & \omega^9 & \omega^3 & \omega^{12} & \omega^6 & \omega^{15} \\
1 & \omega^{10} & \omega^5 & \omega^{15} & \omega^{10} & \omega^5 & \omega^{15} & \omega^{10} & \omega^5 & \omega^{15} & \omega^{10} & \omega^5 & \omega^{15} & \omega^{10} & \omega^5 & \omega^{15} \\
1 & \omega^{11} & \omega^7 & \omega^3 & \omega^{14} & \omega^{10} & \omega^6 & \omega^2 & \omega^{13} & \omega^9 & \omega^5 & 1 & \omega^{11} & \omega^7 & \omega^3 & \omega^{14} \\
1 & \omega^{12} & \omega^9 & \omega^6 & \omega^3 & \omega^{15} & \omega^{12} & \omega^9 & \omega^6 & \omega^3 & \omega^{15} & \omega^{12} & \omega^9 & \omega^6 & \omega^3 & \omega^{15} \\
1 & \omega^{13} & \omega^{11} & \omega^9 & \omega^7 & \omega^5 & \omega^3 & \omega^1 & \omega^{14} & \omega^{12} & \omega^{10} & \omega^8 & \omega^6 & \omega^4 & \omega^2 & \omega^{15} \\
1 & \omega^{14} & \omega^{13} & \omega^{12} & \omega^{11} & \omega^{10} & \omega^9 & \omega^8 & \omega^7 & \omega^6 & \omega^5 & \omega^4 & \omega^3 & \omega^2 & \omega^1 & \omega^{15} \\
1 & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15} & \omega^{15}
\end{array}
\right)
量子フーリエ変換をテンソル積で表現
IBM Qで実装するにあたり,量子回路がイメージしやすいように,テンソル積の表現に直します。なお,$x_i,y_j$は二進数表記です。
\begin{align}
\ket{x} &\xrightarrow{QFT_N}
\frac{1}{\sqrt{N}}\sum_{y=0}^{N-1} e^{\frac{2\pi i}{N}xy}\ket{y}
=\frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1}e^{\frac{2\pi i}{2^n}xy}\ket{y}
=\frac{1}{\sqrt{2^n}}\sum_{y_1=0}^1 \sum_{y_2=0}^1 \cdots \sum_{y_n=0}^1 e^{2\pi ix \left(\sum_{k=1}^n \frac{y_k}{2^k}\right)}\ket{y_1 y_2 \cdots y_n} \\
&=\frac{1}{\sqrt{2^n}} \sum_{y_1=0}^1 \cdots \sum_{y_n=0}^1
\left(e^{2\pi ix \left(\frac{y_1}{2^1}\right)}\ket{y_1} \right) \otimes
\left(e^{2\pi ix \left(\frac{y_2}{2^2}\right)}\ket{y_2} \right) \otimes
\cdots \otimes
\left(e^{2\pi ix \left(\frac{y_n}{2^n}\right)}\ket{y_n} \right) \\
&=\frac{1}{\sqrt{2^n}} \left[
\left(\sum_{y_1=0}^1 e^{2\pi ix \left(\frac{y_1}{2^1}\right)}\ket{y_1} \right) \otimes
\left(\sum_{y_2=0}^1 e^{2\pi ix \left(\frac{y_2}{2^2}\right)}\ket{y_2} \right) \otimes \cdots \otimes
\left(\sum_{y_n=0}^1 e^{2\pi ix \left(\frac{y_n}{2^n}\right)}\ket{y_n} \right)
\right] \\
&=\frac{1}{\sqrt{2^n}}
\left[
\left(\ket{0} + e^{2\pi ix \left(\frac{1}{2}\right)}\ket{1} \right) \otimes
\left(\ket{0} + e^{2\pi ix \left(\frac{1}{2^2}\right)}\ket{1} \right) \otimes \cdots \otimes
\left(\ket{0} + e^{2\pi ix \left(\frac{1}{2^n}\right)}\ket{1} \right)
\right] \\ \\
&\text{ここで,$n$ビットの$x$を二進数表記すると,$x=x_1 2^{n-1} + x_2 2^{n-2} + x_3 2^{n-3} + \cdots + x_{n-1} 2^1 + x_n 2^0$なので,} \\ \\
&=\frac{1}{\sqrt{2^n}}
\left[
\left(\ket{0} + e^{2\pi i \left\{(x_1 2^{n-1}+x_2 2^{n-2}+ \cdots +x_{n-1})+ \frac{x_n}{2}\right\}}\ket{1} \right) \otimes \cdots \otimes
\left(\ket{0} + e^{2\pi i \left\{(x_1 2^{-1}+x_2 2^{-2}+ \cdots +x_n 2^{-n})\right\}}\ket{1} \right)
\right] \\
&=\frac{1}{\sqrt{2^n}}
\left[
\left(\ket{0} + e^{2\pi i (x_n 2^{-1})}\ket{1} \right) \otimes
\left(\ket{0} + e^{2\pi i (x_{n-1}^{-1} + x_n 2^{-2})}\ket{1} \right) \otimes \cdots \otimes
\left(\ket{0} + e^{2\pi i \left\{(x_1 2^{-1}+x_2 2^{-2}+ \cdots +x_n 2^{-n})\right\}}\ket{1} \right)
\right] \\
&=\frac{1}{\sqrt{2^n}}
\left[
\left(\ket{0} + e^{2\pi i (0.x_n)}\ket{1} \right) \otimes
\left(\ket{0} + e^{2\pi i (0.x_{n-1} x_n)}\ket{1} \right) \otimes \cdots \otimes
\left(\ket{0} + e^{2\pi i (0.x_1 x_2\cdots x_n)}\ket{1} \right)
\right]
\end{align}
上述の式より,$\ket{1}$の係数に着目すると,各量子ビットの重ね合わせ状態に対して,位相シフト演算をすれば良さそうです。
位相行列R
位相行列$R_k$を以下のように定義します。
R_{k}=
\left(\begin{array}{cc}
1 & 0 \\
0 & e^{\frac{2\pi i}{2^k}} \\
\end{array}
\right)
すると,$R_1,R_2,R_3,R_4$は次のようになります。
R_{1}=
\left(\begin{array}{cc}
1 & 0 \\
0 & -1 \\
\end{array}
\right) = Z
,
R_{2}=
\left(\begin{array}{cc}
1 & 0 \\
0 & i \\
\end{array}
\right) = S
,
R_{3}=
\left(\begin{array}{cc}
1 & 0 \\
0 & e^{\frac{\pi i}{4}} \\
\end{array}
\right) = T
,
R_{4}=
\left(\begin{array}{cc}
1 & 0 \\
0 & e^{\frac{\pi i}{8}} \\
\end{array}
\right) = \sqrt{T}
IBM Qで実装する際は,これらのゲートを組み合わせることになります。なお,今回は$R_k$を表現できる制御ゲート(cU1)を使用しました。
IBM Qで実装へ!
いよいよ実装です。式変換があと少し残っていますが,それぞれの場合で書き下します。
1量子ビット(N=2)の場合
このとき,量子フーリエ変換は以下のようにアダマール変換と一致します。
ですので,アダマール変換ゲート$H$を使用すれば良いので割愛します。
\ket{x_1} \xrightarrow{QFT_2}
\frac{1}{\sqrt{2}} \left(\ket{0} + e^{2\pi i(0. x_1)}\ket{1} \right) =
\left\{
\begin{align}
\frac{\ket{0}+\ket{1}}{\sqrt{2}} \,(\text{if} \, x_1=0) \\
\frac{\ket{0}-\ket{1}}{\sqrt{2}} \,(\text{if} \, x_1=1)
\end{align}
\right.
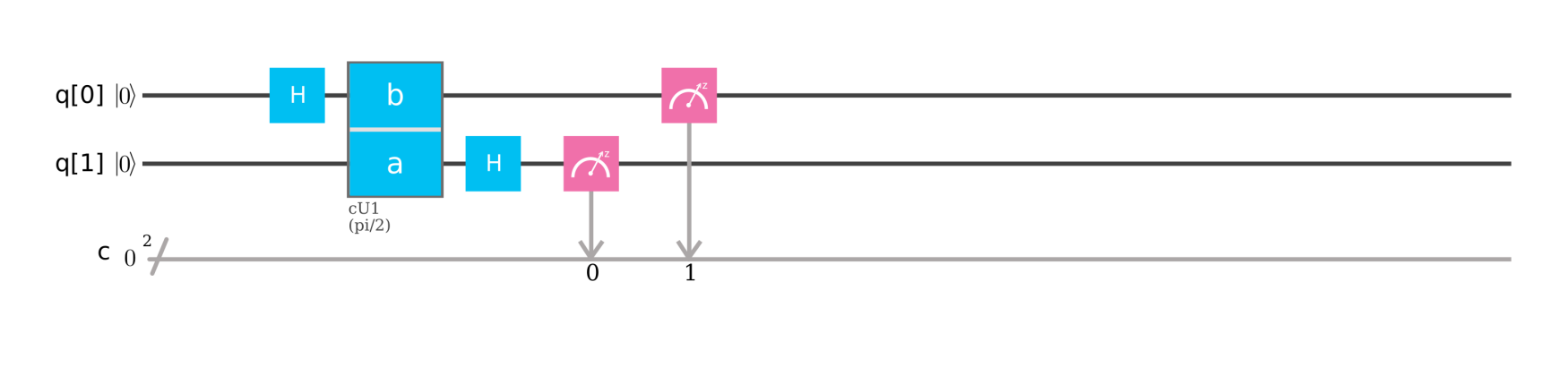
2量子ビット(N=4)の場合
量子フーリエ変換の定義より,下式を満たすゲートを考えます。
\ket{x_1 x_2} \xrightarrow{QFT_4}
\frac{1}{\sqrt{4}}
\left[
\left(\ket{0}+e^{2\pi i(0.x_2)}\ket{1} \right) \otimes
\left(\ket{0}+e^{2\pi i(0.x_1 x_2)}\ket{1} \right)
\right]
1量子ビットに対するアダマール変換が,量子フーリエ変換に一致することを利用して,
次のように変形して定義の式を得ます。使用するのはアダマール変換,制御位相ゲート,(式変形のため恒等変換)です。
$CR_2$は制御$R_2$ゲートであり,IBM QではcU1ゲートを用います。
\begin{align}
\ket{x_1 x_2} &\xrightarrow{H \otimes I}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2}\right)}\ket{1}}{\sqrt{2}}\ket{x_2} \xrightarrow{CR_2}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2}\right)} e^{2\pi i \left(\frac{x_2}{2^2}\right)} \ket{1}}{\sqrt{2}}\ket{x_2} \\
& \xrightarrow{I \otimes H}
\frac{\ket{0}+e^{2\pi i (0.x_1 x_2)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_2)} \ket{1}}{\sqrt{2}}
\end{align}
以上のようにゲートを配置すれば,実装できることがわかりました。
出力されたとき,上位ビットと下位ビットの順序が逆になっていますので,観測した値をレジスタに格納するときだけ注意します。量子フーリエ変換の後にSWAPゲートを用意してもいいかもしれませんね。
IBM Qでは以下のようになります。
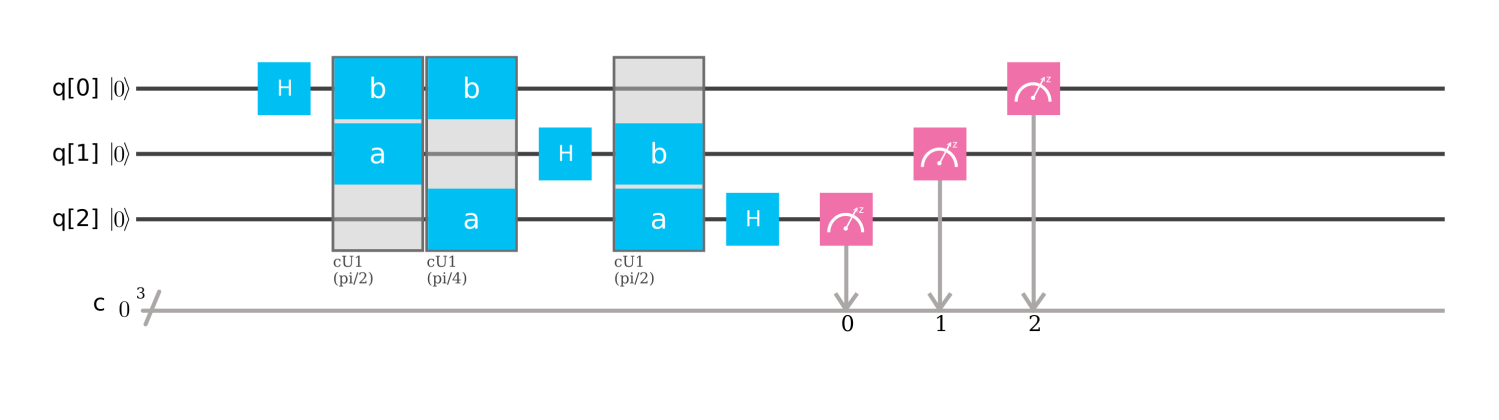
3量子ビット(N=8)の場合
量子フーリエ変換の定義より,下式を満たすゲートを考えます。
\ket{x_1 x_2 x_3} \xrightarrow{QFT_8}
\frac{1}{\sqrt{8}}
\left[
\left(\ket{0}+e^{2\pi i(0.x_3)}\ket{1} \right) \otimes
\left(\ket{0}+e^{2\pi i(0.x_2 x_3)}\ket{1} \right) \otimes
\left(\ket{0}+e^{2\pi i(0.x_1 x_2 x_3)}\ket{1} \right)
\right]
2量子ビットの場合と同様に,ゲートを組みます。
使用するのはアダマール変換,制御位相ゲート,(式変形のため恒等変換)です。
$CR_2,CR_3$はそれぞれ制御$R_2$ゲート,制御$R_3$ゲートであり,IBM QではcU1ゲートを用います。
表記について,例えば$CR_{2,12}$の12では,1を目標ゲート,2を制御ゲートとして表しました。
\begin{align}
\ket{x_1 x_2 x_3} &\xrightarrow{H \otimes I \otimes I}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2}\right)}\ket{1}}{\sqrt{2}}\ket{x_2 x_3}
\xrightarrow{CR_{2,12}} \xrightarrow{CR_{3,13}}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2} + \frac{x_2}{2^2} + \frac{x_3}{2^3} \right)} \ket{1}}{\sqrt{2}}\ket{x_2 x_3} \\
& \xrightarrow{I \otimes H \otimes I}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2} + \frac{x_2}{2^2} + \frac{x_3}{2^3} \right)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_2}{2} \right)} \ket{1}}{\sqrt{2}} \ket{x_3} \\
&\xrightarrow{CR_{2,23}}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2} + \frac{x_2}{2^2} + \frac{x_3}{2^3} \right)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_2}{2} + \frac{x_3}{2^2} \right)} \ket{1}}{\sqrt{2}} \ket{x_3} \\
& \xrightarrow{I \otimes I \otimes H}
\frac{\ket{0}+e^{2\pi i (0.x_1 x_2 x_3)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_2 x_3)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_3)} \ket{1}}{\sqrt{2}}
\end{align}
2量子ビットの場合と同様に,出力されたとき,上位ビットと下位ビットの順序が逆になっていますので,観測した値をレジスタに格納するときだけ注意します。
IBM Qでは以下のようになります。
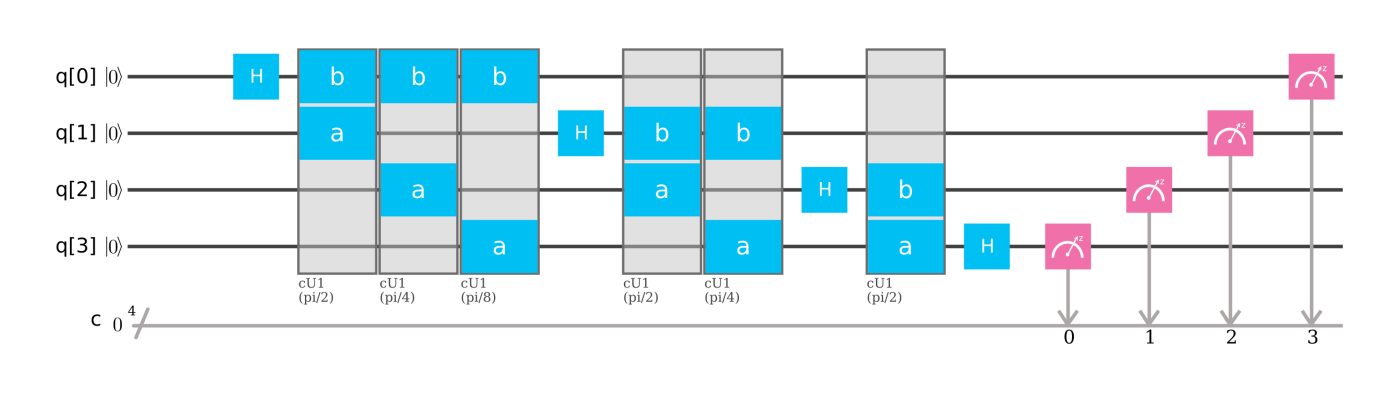
4量子ビット(N=16)の場合
量子フーリエ変換の定義より,下式を満たすゲートを考えます。
\ket{x_1 x_2 x_3 x_4} \xrightarrow{QFT_{16}}
\frac{1}{\sqrt{16}}
\left[
\left(\ket{0}+e^{2\pi i(0.x_4)}\ket{1} \right) \otimes
\left(\ket{0}+e^{2\pi i(0.x_3 x_4)}\ket{1} \right) \otimes
\left(\ket{0}+e^{2\pi i(0.x_2 x_3 x_4)}\ket{1} \right) \otimes
\left(\ket{0}+e^{2\pi i(0.x_1 x_2 x_3 x_4)}\ket{1} \right)
\right]
同様に,ゲートを組みます。
$CR_2,CR_3,CR_4$はそれぞれ制御$R_2$ゲート,制御$R_3$ゲート,制御$R_4$ゲートであり,IBM QではcU1ゲートを用います。
\begin{align}
\ket{x_1 x_2 x_3 x_4} &\xrightarrow{H \otimes I \otimes I \otimes I}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2}\right)}\ket{1}}{\sqrt{2}}\ket{x_2 x_3 x_4}
\xrightarrow{CR_{2,12}} \xrightarrow{CR_{3,13}} \xrightarrow{CR_{4,14}}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_1}{2} + \frac{x_2}{2^2} + \frac{x_3}{2^3} + \frac{x_4}{2^4}\right)} \ket{1}}{\sqrt{2}}\ket{x_2 x_3 x_4} \\
& \xrightarrow{I \otimes H \otimes I \otimes I}
\frac{\ket{0}+e^{2\pi i \left(0.x_1 x_2 x_3 x_4 \right)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i \left(\frac{x_2}{2} \right)} \ket{1}}{\sqrt{2}} \ket{x_3 x_4} \\
&\xrightarrow{CR_{2,23}} \xrightarrow{CR_{3,34}}
\frac{\ket{0}+e^{2\pi i \left(0.x_1 x_2 x_3 x_4 \right)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i \left(0.x_2 x_3 x_4 \right)} \ket{1}}{\sqrt{2}} \ket{x_3 x_4} \\
& \xrightarrow{I \otimes I \otimes H \otimes I}
\frac{\ket{0}+e^{2\pi i (0.x_1 x_2 x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_2 x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (\frac{x_3}{2})} \ket{1}}{\sqrt{2}} \ket{x_4} \\
&\xrightarrow{CR_{2,34}}
\frac{\ket{0}+e^{2\pi i (0.x_1 x_2 x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_2 x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_3 x_4)} \ket{1}}{\sqrt{2}} \ket{x_4} \\
& \xrightarrow{I \otimes I \otimes I \otimes H}
\frac{\ket{0}+e^{2\pi i (0.x_1 x_2 x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_2 x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_3 x_4)} \ket{1}}{\sqrt{2}}
\frac{\ket{0}+e^{2\pi i (0.x_4)} \ket{1}}{\sqrt{2}}
\end{align}
3量子ビットの場合と同様に,出力されたとき,上位ビットと下位ビットの順序が逆になっていますので,観測した値をレジスタに格納するときだけ注意します。
IBM Qでは以下のようになります。
逆量子フーリエ変換して結果を確認
量子フーリエ変換したのち,逆量子フーリエ変換すると,100%の確率で元に戻るはずです。
そこで,4量子ビットの場合を代表として,試してみました。
制御位相ゲートが働く場合も確認するため,入力として$\ket{0000},\ket{1111}$の2パターンで確認しました。
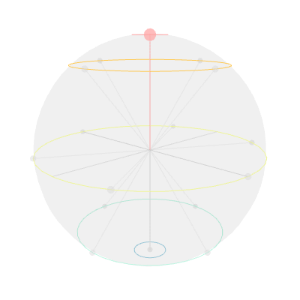
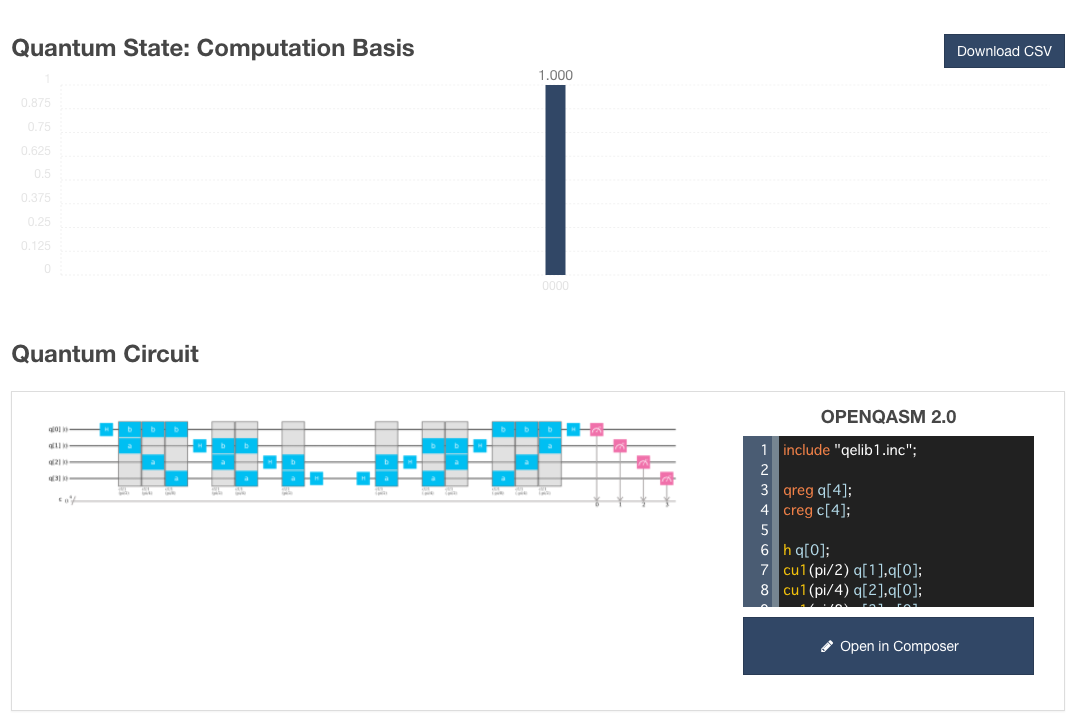
■ $\ket{0000}$の場合
量子回路は以下のようになります。

結果は次のようになりました。
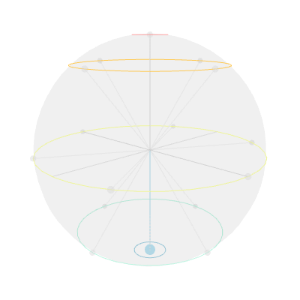
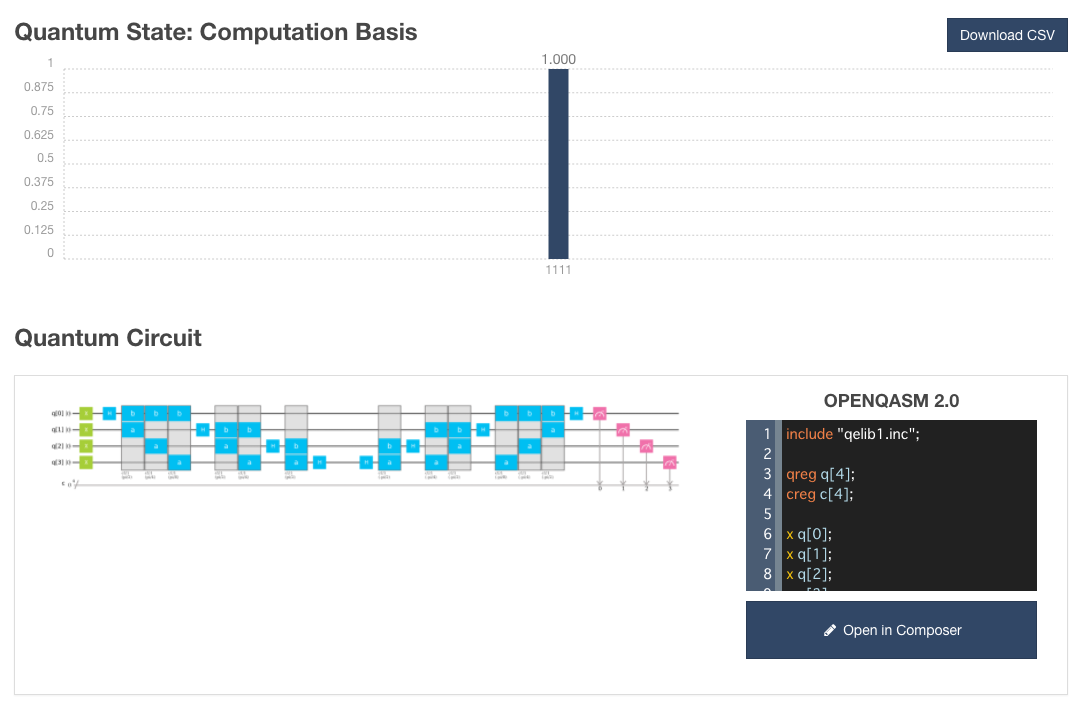
■ $\ket{1111}$の場合
量子回路は以下のようになります。

最後に
ここまで読んでいただきありがとうございました。
今回もシミュレータでしたが,実際に量子計算を試せるというのはワクワクします。
量子フーリエ変換は試せましたので,
今後はショーアのアルゴリズムなどの実装を目標に,少しずつ進められたらと思います。
興味のある方はぜひIBM Q触ってみてください。
(勉強中の身です。誤り等ありましたらご教授いただけると大変嬉しいです。)