この記事は、
「Juliaで学ぶ古典モンテカルロシミュレーション その1:モンテカルロ法による一次元数値積分」
https://qiita.com/cometscome_phys/items/83646da68f1734ea9948
の続きである。
線形代数で考えるマルコフ連鎖
前回までで、ある確率分布関数$P(x)$を用意できれば、局在した被積分関数も精度よく計算できることがわかった。
次の問題は、そのような確率分布関数を常に用意するにはどうすればいいか、ということである。正規分布などの標準的な分布はJuliaにあるので呼び出せば良いが、自分で任意の分布を設定したい時はどうすればよいだろうか?その一つの方法が、マルコフ連鎖モンテカルロ法である。
この記事では、確率の議論を使わずに線形代数を使った考え方で、マルコフ連鎖モンテカルロ法について見てみる。
特に、マルコフ連鎖において確率分布がある分布に収束する原因であるべき乗法について触れ、実際に実装して確かめてみる。
確率分布を得る、とは
ある確率分布$P(x)$に従う変数$x$の分布が欲しい。
$x$が連続変数だと何かと面倒なので、離散変数としよう。つまり、$N$個の$x_i$が何かの分布関数$P(x_i)$に従っていることを考える。
例えば、正規分布であれば、
using Distributions
using Plots
N = 100
x = range(-10,10,length=N)
m = Normal(0,1)
f(x) = pdf(m,x)
plot(x,f)
という分布となる。
確率、というのは(自分にとっては)わかりにくいので、もう少し具体的に考えたい。
重みつきモンテカルロ積分では何回も乱数を振って$x_i$を得る。ここで、$M$回$x_i$を得たとしよう。そして、$M$回の試行で$x_i$を何回得られたかを表す数を$N^M(x_i)$とする。
十分に$M$が大きい時を考える。
もし一様分布であれば、$N^M(x_1)=N^M(x_2)=,\cdots,N^M(x_{M})$となる。正規分布であれば、上のグラフに$M$をかけたものが$N^M(x_i)$となる。
$M$を増減させることを考えると、どんどん増えていく$N^M$よりも、試行回数で割った$N^M/M$の方がわかりやすい。つまり、$P(x_i)$を使った方が良い。まさにこれは確率である。
乱数の回数を1回増やし、$M+1$番目の選ばれた変数を$x_i^{M+1}$とすると、
$$
N^{M+1}(x_i) = N^{M}(x_i) + 1
$$
となる。確率で書けば、
$$
P^{M+1}(x_i) = \frac{N^{M+1}(x_i)}{M+1} = \frac{N^{M}(x_i) + 1}{M+1}
$$
となり、$M$は十分に大きい時$M+1 \sim M$となるので
$$
P^{M+1}(x_i) = P^M(x_i)
$$
が得られる。つまり、一回増やしたところで確率分布が変わらない状態、定常状態である。この状態であれば、常に$x_i$の確率分布は$P(x_i)$である、と言える。
さて、ここまでの議論の中で、"乱数の回数を1回増やし"、の部分が不明であることがわかる。どのように$x_i$を選べば定常状態になるのだろうか?
$M$番目にとっていた変数を$x_j$としよう。
$x_j$は、ある確率$T(j \rightarrow i)$で$x_i$になるとする。
そして、この確率$T$は$M$回めより前の状態に寄らないとする(マルコフ連鎖)。
この時、
$M$番目に$x_j$が選ばれていた確率は$P^M(x_j)$であり、「$x_j$が選ばれていた状態で次が$x_i$になる確率」、すなわち、条件付き確率、は$T(j \rightarrow i)$である。
そして、$M+1$番めに$x_i$が選ばれる確率$P^{M+1}(x_i)$は、
$$
P^{M+1}(x_i) = \sum_j T(j \rightarrow i)P^M(x_j)
$$
と書ける。十分に大きな$M$のとき、$P^{M+1}(x_i) = P^M(x_i)$を使うと、
$$
P(x_i) = \sum_j T_{ij} P(x_j)
$$
となる。ここで、$T(j \rightarrow i) \equiv T_{ij}$とかきかえた。その結果、
$T_{ij}$を行列$T$の成分とみなすことができ、$N$次元のベクトル${\bf y} =(P(x_1),\cdots,P(x_N))^T$を用意すれば、
$$
T {\bf y} = {\bf y}
$$
が$M$が大きい時成り立つ必要がある。このような$T$を作る方法を考えよう。
まず、我々は一様乱数しか使えないとしよう。つまり、$1$回めの試行は一様乱数によって$x_i$が選ばれるとする。
この時の確率分布を$P^1(x_i) = P_{\rm uniform}(x_i)$とする。この分布から作ったベクトルを
${\bf y}^0 = (P_{\rm uniform}(x_1),\cdots,P_{\rm uniform}(x_N))^T$とする。
もし、このベクトル${\bf y}^0$に$T$を$M$回作用させた結果、
$$
T^M {\bf y}^0 \sim {\bf y}
$$
が得られたとすれば、$M+1$回めには
$$
T {\bf y} = {\bf y}
$$
が成り立つことになる。
つまり、
適当な${\bf y}^0$から出発して$T$をたくさん作用させ、最終的に${\bf y}$に収束するような行列$T$を作ることができればよい。
ベクトルの収束とべき乗法
ある同じ行列を何回もかけた時、得られるベクトルは収束するのだろうか?
実は、固有値と固有ベクトルを求める手法であるべき乗法と呼ばれる手法では、全く同じことを行っている。
行列$A$が固有値$\lambda_{n}$と固有ベクトル${\bf y}_{n}$を持つとする:
A {\bf y}_n = \lambda_n {\bf y}_n
この時、任意のベクトル${\bf y}^0$を$A$の固有ベクトルで
{\bf y}^0 = \sum_n c_n {\bf y}_n
で展開できる。$c_n$は展開係数である。
このベクトルに$M$回$A$をかけてみると、
A^M{\bf y}^0 = \sum_n c_n (\lambda_n)^M {\bf y}_n
となる。ここで、固有値$\lambda_n$を絶対値と位相に分けると$\lambda_n = |\lambda_n| e^{i \phi_n}$となり、
A^M{\bf y}^0 = \sum_n c_n |\lambda_n|^M e^{i M \phi_n} {\bf y}_n
が得られる。すべての固有値$\lambda_n$に対して$|\lambda_n|<1$であれば、この操作は収束し、絶対値最大の固有値$\lambda_{max}$を持つ固有ベクトル
\lim_{M \rightarrow \infty} A^M{\bf y}^0 = c_{max} |\lambda_{max}|^M e^{i M \phi_{max}} {\bf y}_{max}
となる。
つまり、行列を複数回かけるだけで絶対値最大固有値を持つ固有ベクトルを得ることができるのである。
べき乗法のテスト
べき乗法のテストをしてみよう。十分な回数行列$A$をかけた時、$M+1$番目のベクトルと$M$番目のベクトルには
{\bf y}^{M+1} = A {\bf y}^M = \lambda_{max} {\bf y}^M
となっているので、内積が${\bf y}^M \cdot {\bf y}^M = 1$と規格化されていれば、
\lambda_{max} = {\bf y}^{M+1} \cdot {\bf y}^M
で絶対値最大の固有値を得ることができる。
まず、乱数によって適当に行列$A$を作ろう。ここで、以後の議論のために、行列要素は$A_{ij}>0$となるように乱数を振ってみる。
using Random
function make_A(n,乱数シード)
Random.seed!(乱数シード)
mat_A = rand(n,n)
return mat_A
end
Juliaではrand(n,n)で$n \times n$の乱数の入った行列を作ってくれるので便利である。
作った行列の固有値を見てみると、
using LinearAlgebra
mat_A = make_A(10,123)
λ,y = eigen(mat_A)
println("λ = ", λ)
println("|λ| = ", abs.(λ))
λ = Complex{Float64}[5.31627+0.0im, -0.186064+0.701151im, -0.186064-0.701151im, 0.81506+0.0im, 0.332553+0.572704im, 0.332553-0.572704im, -0.363697+0.135496im, -0.363697-0.135496im, 0.278787+0.073673im, 0.278787-0.073673im]
|λ| = [5.31627, 0.725419, 0.725419, 0.81506, 0.662255, 0.662255, 0.388117, 0.388117, 0.288357, 0.288357]
となる。この行列の絶対値は$1$を超えているので、このままでは漸化式
{\bf y}^{M+1} = A {\bf y}^M
は発散してしまう。値の発散を避けるために、
{\bf y}^{M+1} = A {\bf y}^M \frac{1}{\sqrt{{\bf y}^M \cdot {\bf y}^M}}
として、毎回ベクトルを規格化することにする。ベクトルの規格化は固有ベクトルの大きさにのみ影響を与えるので、
固有値及び固有ベクトルの成分比には影響を与えない。
十分大きな$M$では、
{\bf y}^{M+1} \cdot {\bf y}^M = \lambda_{max}
となり、この量をモニターしていれば、固有値が得られているかわかる。
さて、実装してみよう。
function べき乗法(M,mat_A,y0)
y = zeros(typeof(y0[1]),length(y0))
yold = zeros(typeof(y0[1]),length(y0))
c = sqrt(dot(y0,y0))
y[:] = y0[:]/c
yold[:] = y0[:]/c
λ = Float64[]
ind = Int64[]
for i in 1:M
y = mat_A*y
push!(λ,dot(y,yold))
c = sqrt(dot(y,y))
y = y/c
yold = y
push!(ind,i)
end
return ind,λ,y
end
ただひたすらに行列をかけて、規格化すればよい。
eigen(A)では絶対値最大の固有値が最初に来るので、それで割ることで精度を見てみると、
N = 10
mat_A = make_A(N,123)
y0 = rand(N)
M = 10
ind,λ,y = べき乗法(M,mat_A,y0)
println("べき乗法の固有値 = ",λ[end])
λe,ye = eigen(mat_A)
println("対角化による絶対値最大固有値 = ",λe[1])
plot(ind,λ/abs(λe[1]))
べき乗法の固有値 = 5.316268942890086
対角化による絶対値最大固有値 = 5.316268947339038 + 0.0im

となり、あっという間に収束していることがわかる。行列のサイズを大きくすると
N = 1000
mat_A = make_A(N,123)
y0 = rand(N)
M = 10
ind,λ,y = べき乗法(M,mat_A,y0)
println("べき乗法の絶対値最大固有値 = ",λ[end])
λe,ye = eigen(mat_A)
println("対角化による絶対値最大固有値 = ",λe[1])
plot(ind,λ/abs(λe[1]))
べき乗法の絶対値最大固有値 = 500.05210910716227
対角化による絶対値最大固有値 = 500.052109107162 + 0.0im
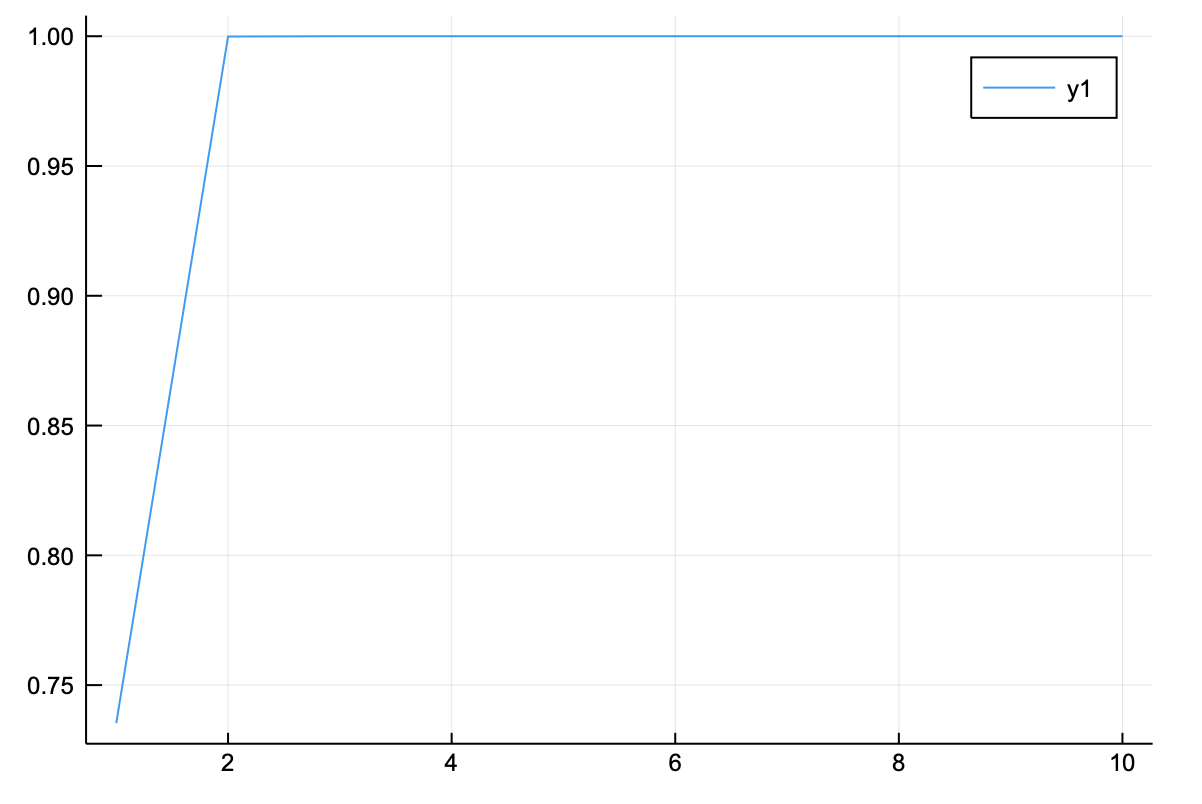
これもあっという間に収束する。この収束の速度は、絶対値最大の固有値と絶対値で二番目に大きい固有値の大きさの比で決まる。
今回の行列では、
println(λe[1:2])
Complex{Float64}[500.052+0.0im, -7.23261+5.99742im]
と非常に大きな差があるため、素早く収束した。
さて、ここまでの計算で気づいたかもしれないが、今考えている行列の固有値の絶対値最大は実数となっている。
これは偶然ではなく、「ペロン=フロベニウスの定理」によって保証されているのである。
https://ja.wikipedia.org/wiki/ペロン=フロベニウスの定理
この定理では、行列要素のすべてが正の実数の場合、固有値の中で絶対値が最大のもの$r$は正の実数であることを示している。
そしてこの$r$は
{\rm min}_i \sum_j A_{ij} \le r \le {\rm max}_i \sum_j A_{ij}
という不等式を満たす。
この不等式を確かめてみよう。
function 部分和(mat_A,N)
和 = zeros(Float64,N)
for i in 1:N
for j in 1:N
和[i] += mat_A[i,j]
end
end
return 和
end
N = 1000
mat_A = make_A(N,123)
和 = 部分和(mat_A,N)
最大値 = maximum(和)
最小値 = minimum(和)
ind,λ,y = べき乗法(M,mat_A,y0)
println("最小値: ",最小値, " べき乗法の絶対値最大固有値: ",λ[end]," 最大値: ",最大値)
最小値: 472.37515410622404 べき乗法の絶対値最大固有値: 500.05210910716227 最大値: 531.3016496577754
となるので、ちゃんと不等式を満たしている。
そして実は、確率分布の生成において考えている行列$T$において、ペロン=フロベニウスの定理を使うことができる。つまり、行列$T$は
T_{ij} > 0
を満たすことができる。なぜならば、$T_{ij}$は確率であるため、常に非負でなければならないからである。
そして、ある$x_j$からすべての状態$x_i$に遷移できる(エルゴート性がある)ことを要請すれば、常に正にできる。
マルコフ連鎖の収束
$T$を何回もかければ絶対値最大の固有値を持つ固有ベクトルに収束することは確認できた。
つまり、
{\bf y}^{M+1} = T {\bf y} = \lambda_{max} {\bf y}
となる行列$T$は存在する。
そして、$\lambda_{max}$はペロン=フロベニウスの定理より正の実数である。
確率分布を生成するためには、$\lambda_{max} = 1$としなければならない。ここで、不等式を使ったはさみうちを使う。つまり、
任意の$i$において
\sum_j T_{ij} = 1
が成りたてば、不等式は
1 \le r \le 1
となり、$\lambda_{max} = 1$となる。
ここで、$\sum_j T_{ij} = 1$という条件は、確率の総和が1であることに他ならない! $x_j$から$x_i$に遷移するとき、すべての$x_j$を考慮すれば
、どれかからは遷移する。つまり、この和が成り立つ。 また、$x_j$は必ずどれかの$x_i$に遷移するので、
\sum_i T_{ij} = 1
も成り立つ。
以上から、$T$が確率である、ということからベクトルは収束することがわかった。
次は、${\bf y}$を収束したベクトルとして持つような$T$を設計する。 なお、この行列$T$は遷移行列と呼ぶことが多い。
遷移行列Tの設計と詳細釣り合い条件
{\bf y} = T {\bf y}
となるような$T$を設計したい。
この式を成分表示すると、
y_i = \sum_j T_{ij} y_j
である。ここで、
\sum_j T_{ji} = 1
を用いれば、
\left(\sum_j T_{ji} \right) y_i = \sum_j T_{ij} y_j
\sum_j T_{ji} y_i = \sum_j T_{ij} y_j
となる。これを満たすような行列$T$を設計すればよい。
一番単純なのは、各$j$において
T_{ji} y_i = T_{ij} y_j
が成り立つように$T$を設計することである。
これを「詳細釣り合い条件」と呼び、様々なマルコフ連鎖モンテカルロ法で使われている。
詳細釣り合い条件を満たす遷移行列$T$の設計
さて、この詳細釣り合い条件を満たした行列$T$を設計するとしよう。
この条件は、
\frac{T_{ji}}{T_{ij}} = \frac{y_j}{y_i}
と比の形で書き直すことができる。そして、それぞれの$T_{ij}$は正の実数であるという条件のみが課されており、
この比さえ保っていればどんな値でもよい。
メトロポリス・ヘイスティングス法
上の比を満たす行列$T$を設計してみよう。
まず、$T_{ij}$は「$x_j$が選ばれていた状態で次が$x_i$になる確率」であるが、これは、
「$x_j$が選ばれていた状態で$x_i$を提案する確率$ g(x_j \rightarrow x_i)$」と「$x_j$が選ばれていた状態で$x_i$を採択する確率$A(x_j \rightarrow x_i)$」の二つ:
T_{ij} = g(x_j \rightarrow x_i) A(x_j \rightarrow x_i)
に分解することができる。
イジング模型の場合、$g(x_j \rightarrow x_i)$は、
$N$個の格子点の中からランダムに一つ選ぶ確率であり、$1/N$となる。この場合、直前の状態が何であってもよいので、
$g(x_j \rightarrow x_i) = g(x_i \rightarrow x_j)$である。
詳細釣り合い条件は、
\frac{g(x_i \rightarrow x_j) A(x_i \rightarrow x_j)}{g(x_j \rightarrow x_i) A(x_j \rightarrow x_i)} = \frac{y_j}{y_i}
\frac{ A(x_i \rightarrow x_j)}{ A(x_j \rightarrow x_i)} = \frac{g(x_j \rightarrow x_i)}{g(x_i \rightarrow x_j)} \frac{y_j}{y_i}
となり、採択確率$A$の比の条件に変化する。
上の比を満たす$A(x_i \rightarrow x_j)$として単純なのは、
$A(x_j \rightarrow x_i) = 1$とおき、
A(x_i \rightarrow x_j) = \frac{g(x_j \rightarrow x_i)}{g(x_i \rightarrow x_j)} \frac{y_j}{y_i}
とするものである。
ただし、$g(x_j \rightarrow x_i) y_j > g(x_i \rightarrow x_j) y_i$では値が1を超えてしまうので、その時には確率1で遷移するとする。つまり、$x_i$から$x_j$への遷移が受け入れられる確率$A(x_i \rightarrow x_j)$は
A(x_i \rightarrow x_j) = {\rm min} \left(1,\frac{g(x_j \rightarrow x_i)}{g(x_i \rightarrow x_j)} \frac{y_j}{y_i}\right)
となる。これがメトロポリス・ヘイスティングス(M-H)法の採択確率である。
単純な場合、つまり、提案確率が対称な場合($g(x_j \rightarrow x_i) = g(x_i \rightarrow x_j)$)、
これは
A(x_i \rightarrow x_j) = {\rm min} \left(1, \frac{y_j}{y_i}\right)
となる。これはいわゆるメトロポリス法の採択確率である。
$y_i$は確率であるので、より大きな確率$y_j$を持つ$x_j$を候補とした場合には間違いなく遷移する、ということを意味している。
熱浴法
次に、別の方法を考えてみよう。
条件
\frac{T_{ji}}{T_{ij}} = \frac{y_j}{y_i}
を満たすためには、
T_{ji} = c y_j
でもよい。つまり、分子同士が等しく、分母同士が等しい場合である。ここで$c$は適当な係数である。
この場合、$x_i$が何であっても、$x_i$から$x_j$へ遷移する確率は$y_j$に比例する。
ただし、行列$T$には
\sum_j T_{ji} = 1
という条件があるので、$c$は
c \sum_j y_j = 1
より
c = \frac{1}{\sum_j y_j}
となる。つまり、遷移行列を
T_{ji} = \frac{y_j}{\sum_j y_j}
と設計することができる。
これが一番基本的な「熱浴法」の遷移行列である。
しかし、このままでは実用的ではないため、以下の方法を用いる。
$L$次元の問題を考える。つまり、変数は$L$次元ベクトル${\bf x} = (x^1,x^2,\cdots,x^L)^T$であり、
あるベクトル${\bf x}$が実現する確率を$P({\bf x})$とする。
また、それぞれの次元での座標$x^i$は離散的になっており、$n$個座標があるとする。
その結果、可能なすべてのベクトルの組み合わせは$N = n^L$という膨大な数になる。
ここでは、簡単のため、$L=2$の場合を考える。この時、${\bf x}=(x^1,x^2)^T$である。
ある座標${\bf x}$を実現するための確率$P({\bf x})$は、
P({\bf x}) = P(x_1|x_2)P(x_2)
と、書くことができる。ここで、$P(x_1|x_2)$は2番目の次元の座標が$x_2$である時に、$x_1$が選ばれる条件付き確率である。
また、$P(x_2)$は、2番目の次元の座標が$x_2$である確率:
P(x_2) = \sum_i P(x_i,x_2)
である。
今、${\bf x} = (x_1,x_2)^T$から${\bf x}' = (x_1',x_2)$へと遷移する場合を考える。この時、
P({\bf x}') = P(x_1'|x_2)P(x_2)
なので、詳細釣り合い条件は
\frac{T_{{\bf x} \rightarrow {\bf x}'}}{T_{{\bf x}' \rightarrow {\bf x}}} = \frac{P({\bf x}')}{P({\bf x})}
= \frac{P(x_1'|x_2)P(x_2)}{P(x_1|x_2)P(x_2)} = \frac{P(x_1'|x_2)}{P(x_1|x_2)}
となる。
よって、遷移行列を
T_{{\bf x} \rightarrow {\bf x}'} = P(x_1'|x_2)
とすれば、詳細釣り合い条件を満たすことができる。
これは、
T_{{\bf x} \rightarrow {\bf x}'} = \frac{P({\bf x}')}{P(x_2)}
とも書けるので、$c = 1/P(x_2)$とした熱浴法(あるいはギブスサンプリング法)である。なお、熱浴法は採択率が常に1のM-H法の一種であることを示すことができる(参考文献参照)。
一般には、条件付き確率$P(x_1'|x_2)$に従ってサンプリングすることが難しいため、熱浴法は適用できる問題が限られる。 例えば、この条件付き確率が正規分布になるようなケースでは、利用されている。
イジング模型では、$x_1$が$\pm 1$の二通りしかとらないために、一様乱数$r$を発生させて、$r < P(+1|x_2)$の時には$x_1=+1$、それ以外では$-1$とすることで、この条件付き確率によるサンプリングを実行できる。 次回以降の記事では、イジング模型での$P(x_1'|x_2)$の値について述べる。
参考文献
C.M.ビショップ,「パターン認識と機械学習 下」 丸善出版 (2012)