モンテカルロ法による一次元数値積分
古典スピン系の模型である、イジング模型の重みつきモンテカルロシミュレーションをやってみよう。
Julia言語を使うことで、びっくりするほど簡単にモンテカルロシミュレーションができることを示してみよう。
一回目のこの記事では、ターゲットとするイジング模型の紹介と、その物理量を計算するためのモンテカルロ法について解説する。
なお、Juliaでは確率分布関数を簡単に生成できるので、一回目では、マルコフ連鎖を使わずに一次元のモンテカルロ積分をやってみる。
バージョン
Julia 1.1
なお、この記事は
https://github.com/cometscome/MC
のJulia 0.6版の記事をJulia 1.1版に書き換えたものである。
ハミルトニアンと分配関数
まず、古典スピン系であるイジング模型のハミルトニアンは
$$
H = -j \sum_{\langle i j \rangle} \sigma_i \sigma_j
$$
である。ここで、$\langle i j \rangle$は、最隣接格子点のみで和を取ることを意味しており、一次元系であれば、$j=i+1$などである。
$\sigma_i$は$i$番目の格子点のスピンを表し、$+1$か$-1$を取る。
統計力学において、物理量$A$の期待値は
$$
\langle A \rangle = \frac{1}{Z} \sum_{\cal C} \left[ \exp \left( -\frac{H({\cal C})}{k_{\rm B} T} \right) A({\cal C}) \right]
$$
と書ける。ここで、$H({\cal C})$は、あるスピン配置${\cal C}$でのハミルトニアン、$A({\cal C})$はその時の物理量$A$の値である。
$k_{\rm B}$はボルツマン定数、$T$は温度である。
$Z$は分配関数であり、
$$
Z = \sum_{\cal C}\exp \left( -\frac{H({\cal C})}{k_{\rm B} T} \right)
$$
と定義されている。
つまり、すべての可能なスピン配置に関して和を取れば、物理量が計算できる。
すべての可能なスピン配置の数${\cal N}$は、$N$個の格子点を持つ系の場合、各サイトで$-1$か$1$の二通りの状態を取れるので、
$$
{\cal N} = 2^N
$$
である。
$10 \times 10$の二次元イジング模型ですら
N=10*10
println(2.0^N)
1.2676506002282294e30
$10^{30}$もの配置の数がある。こんなに膨大な数を足しあげるのは現実的ではない(時にはやらなければならないこともあるが)。
そのため、そのまま足し上げずに済む方法を考える必要がある。
膨大な数の効率的な足しあげは高次元積分を行うのとほとんど等しいので、以下では、高次元積分の数値的実行法について見てみる。
モンテカルロ法
次に、乱数を使ってこの物理量の計算を試みてみよう。
モンテカルロ法とは、高次元の積分を効率的に計算するアルゴリズムの一つである。
ある高次元積分を
$$
I = \int d{\bf x} P({\bf x}) f({\bf x})
$$
とする。ここで、${\bf x}$は${\cal N}$次元ベクトルであり、積分の次元は${\cal N}$である。以下で、様々な方法で積分を実行してみる。
数値積分
簡単のため、1次元積分${\cal N}=1$を考える:
$$
I = \int_{x_{\rm min}}^{x_{\rm max}} dx P(x) f(x)
$$
この積分を数値的に実行するためには、$dx$を微小な間隔だとみなして足し上げればよい。足し上げの総数を$n$とすると、
$$
dx = \frac{x_{\rm max} - x_{\rm min}}{n-1}
$$
とし、
$$
x_i = (i-1)dx + x_{\rm min}
$$
とすれば、
$$
I \sim \sum_{i=1}^{n} dx P(x_i) f(x_i)
$$
で積分を計算できる。
さて、以下の積分:
$$
I = \int_{-\infty}^{\infty} dx e^{-x^2/\xi^2}
$$
を実行してみよう。解析解は
$$
I = \xi \sqrt{\pi}
$$
である。
$\xi=0.1$の時の被積分関数は
using Plots
n = 100
x = range(-1,1,length=n)
ξ = 0.1
f(x) = exp(-x^2/ξ^2)
plot(x,f)
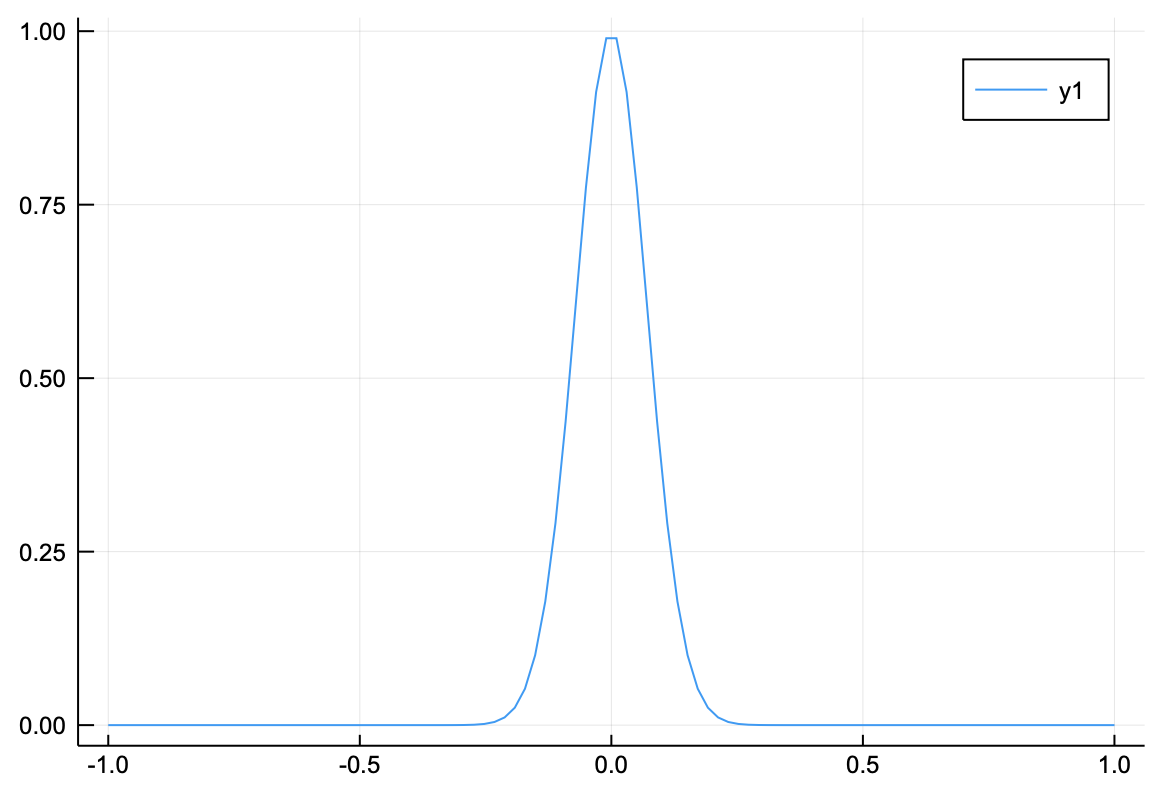
である。単純に足しあげて積分をしてみよう。
単純な積分をするfunctionを以下に定義する。Juliaではfunctionの名前にUnicodeが使えるので、日本語を使うことができる。
function 積分(n,f,xmin,xmax)
dx = (xmax-xmin)/(n-1)
和 = 0.0
for i in 1:n
xi = (i-1)*dx+xmin
和 += f(xi)
end
和 = 和*dx
return 和
end
試しに刻みの数を100として解析解を比べてみると
n = 100
x = range(0,1,length=n)
ξ = 0.1
f(x) = exp(-x^2/ξ^2)
解析解= ξ*sqrt(π)
xmin = -1.0
xmax = 1.0
和 = 積分(n,f,xmin,xmax)
println("解析解 = ", 解析解, " 数値和 = ",和)
解析解 = 0.1772453850905516 数値和 = 0.1772453850905516
となる。
刻み幅を増やしていくと、数値積分と解析解の比は
function 刻み幅依存性(ξ,dn)
和 = zeros(Float64,20)
xmin = -1.0
xmax = 1.0
f(x) = exp(-x^2/ξ^2)
vecn = Int64[]
for i in 1:20
n = i*dn
和[i] = 積分(n,f,xmin,xmax)
push!(vecn,n)
end
return 和,vecn
end
ξ=0.01
和,vecn = 刻み幅依存性(ξ,20)
解析解= ξ*sqrt(π)
plot(vecn,和/解析解)
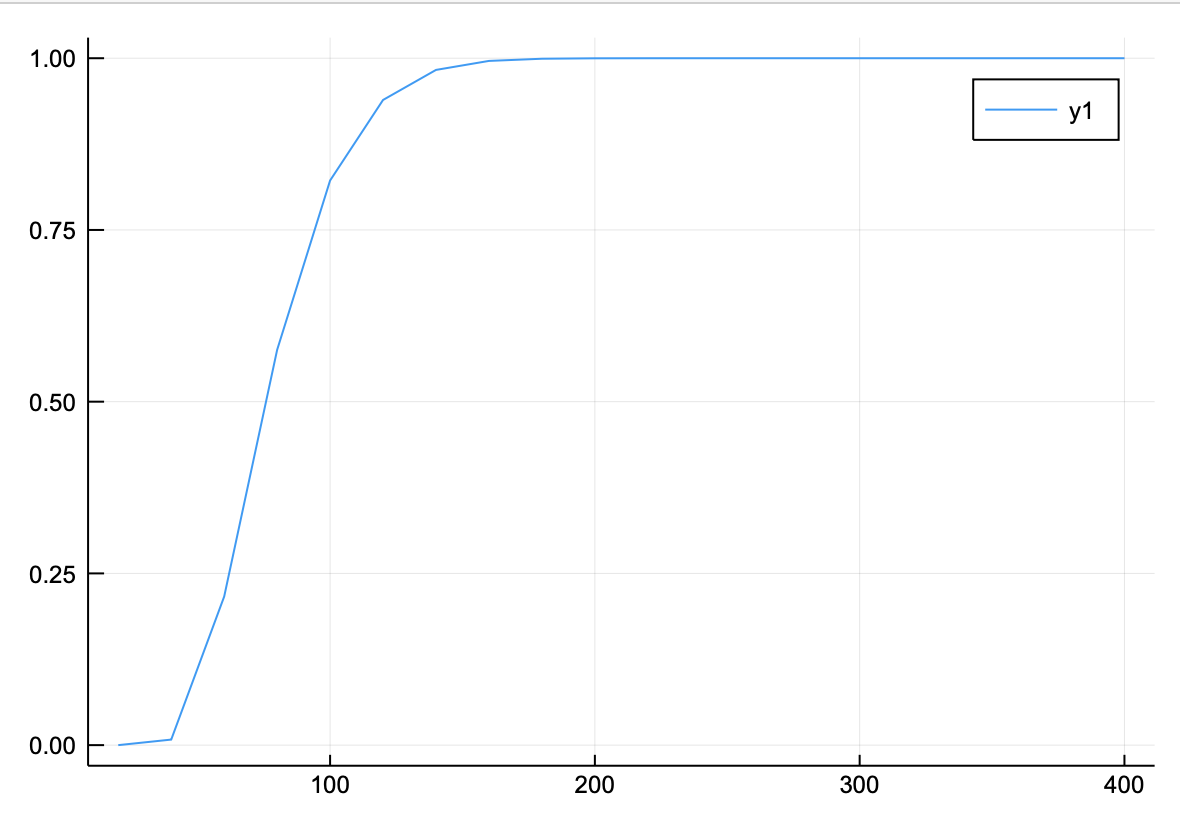
となる。だんだんと近づいていく。さらに、$\xi = 0.001$とすると、
ξ=0.001
和,vecn = 刻み幅依存性(ξ,100)
解析解= ξ*sqrt(π)
plot(vecn,和/解析解)
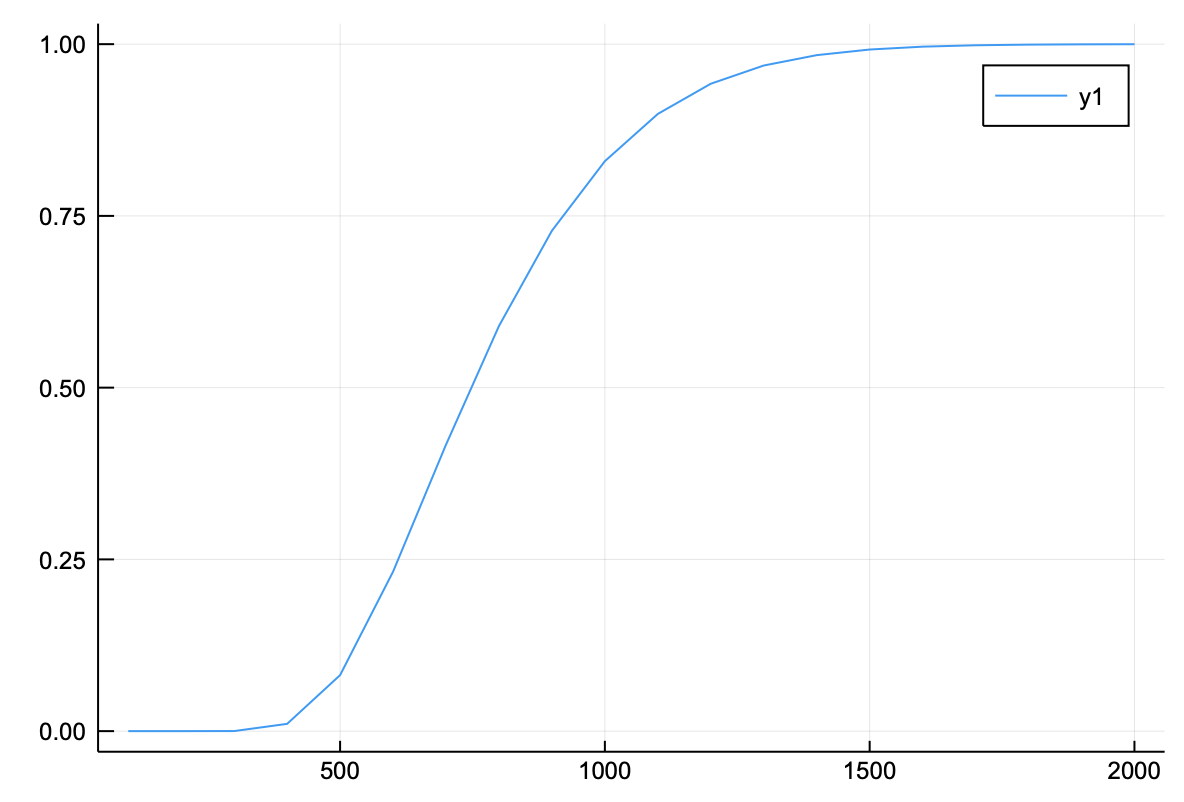
となり、必要な点の数は増える。
単純モンテカルロ法
次に、単純モンテカルロ法を考えてみよう。
積分
$$
I = \int_{-\infty}^{\infty} dx e^{-x^2/\xi^2}
$$
を、一様に生成される乱数$x_i$を用いて計算してみよう。
まず、被積分関数が1のとき、
$$
I = \int_{x_{min}}^{x_{max}} dx = x_{max} - x_{min}
$$
であるが、これを$n$個の$x_i$のランダムな和で計算しようとすると、
$$
I \sim \frac{x_{max} - x_{min}}{n} \sum_{i = 1}^n 1
$$
とすればよい。つまり、
$$
I \sim \frac{x_{max}-x_{min}}{n} \sum_{i=1}^n e^{-x_i^2/\xi^2}
$$
を計算すれば、積分が近似できる。
では、実際にやってみよう。
function モンテカルロ積分(n,f,xmin,xmax)
和 = 0.0
for i in 1:n
xi = (xmax-xmin)*rand()+xmin
和 += f(xi)
end
和 = 和*(xmax-xmin)/n
return 和
end
とモンテカルロ積分を定義して、解析解との比のサンプル数依存性を見てみると、
function サンプル数依存性(ξ,dn)
和 = zeros(Float64,20)
xmin = -1.0
xmax = 1.0
f(x) = exp(-x^2/ξ^2)
vecn = Int64[]
for i in 1:20
n = i*dn
和[i] = モンテカルロ積分(n,f,xmin,xmax)
push!(vecn,n)
end
return 和,vecn
end
using Random
Random.seed!(123)
ξ=0.01
和,vecn = サンプル数依存性(ξ,300)
解析解= ξ*sqrt(π)
plot(vecn,和/解析解)
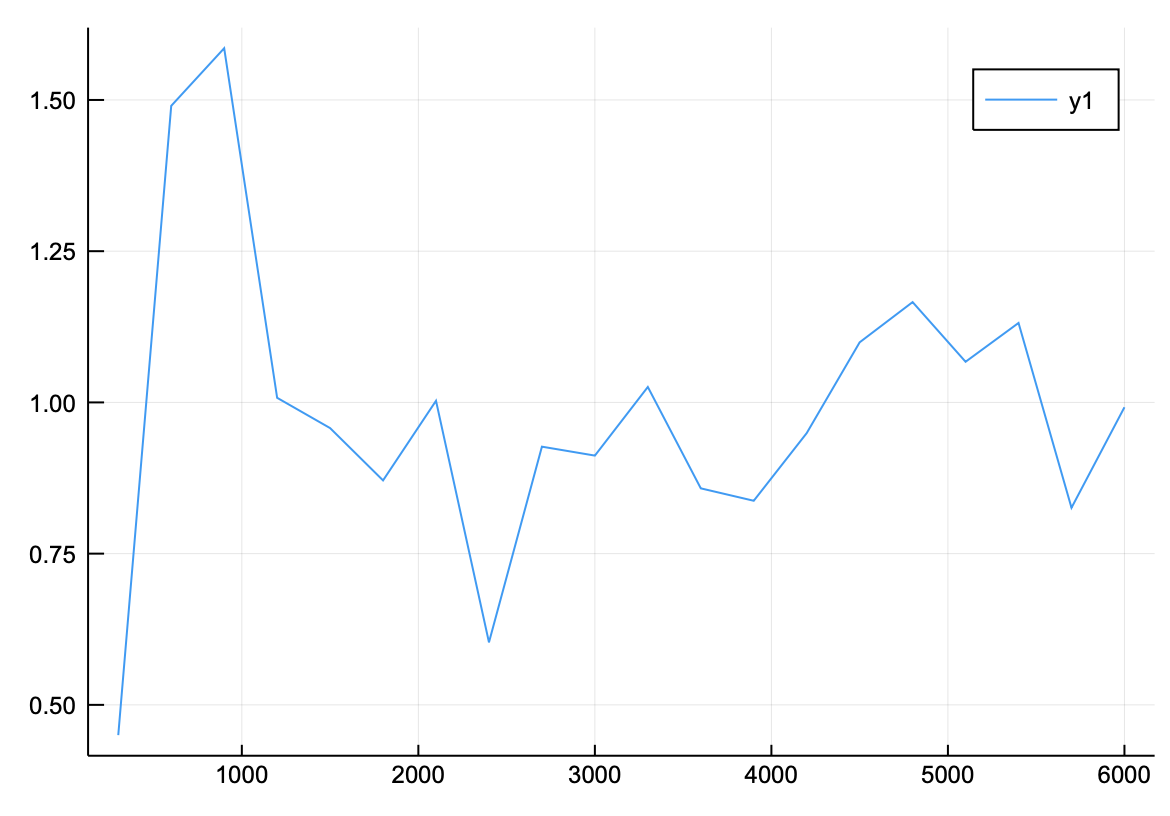
となる。6000個もとっているのもかかわらず、普通の積分より精度が低いことがわかる。もっと増やしてみると、
ξ=0.01
和,vecn = サンプル数依存性(ξ,10000)
解析解= ξ*sqrt(π)
plot(vecn,和/解析解)
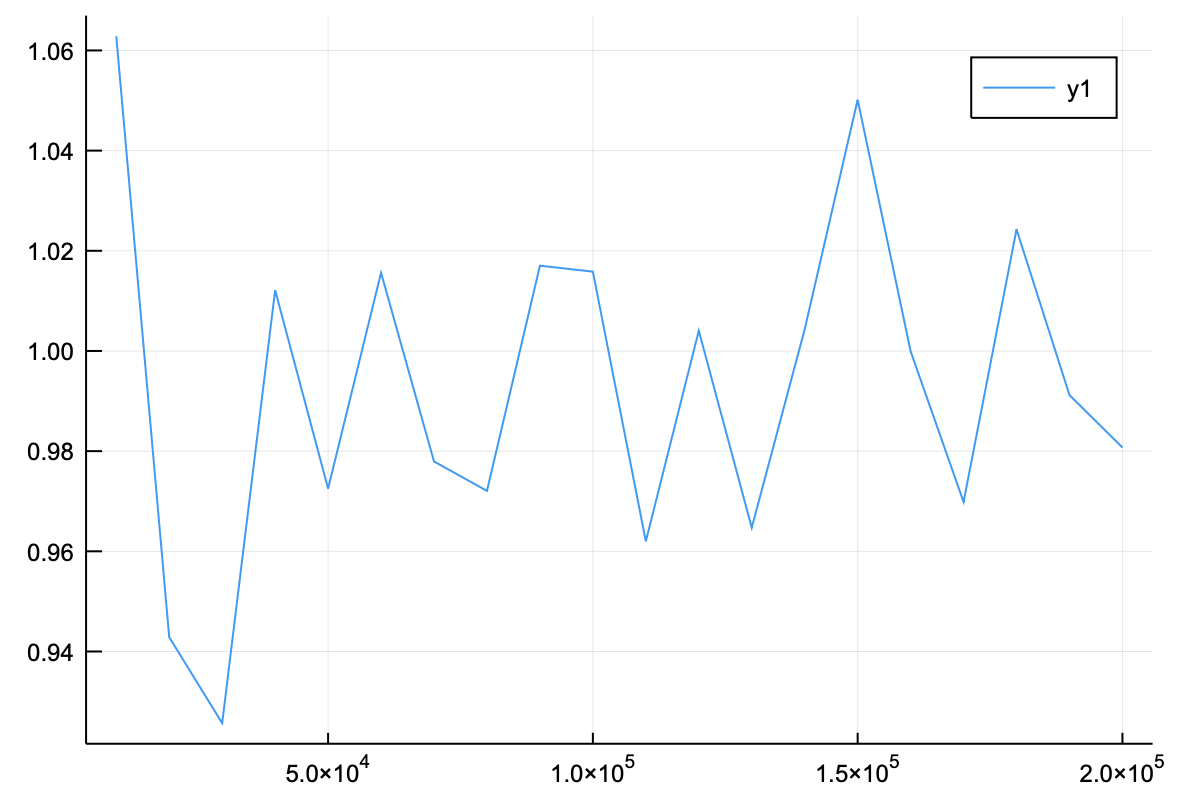
となり、精度が上がるが、それでも普通に数値積分するのと比べて精度が悪い。
さらに$\xi = 0.001$とすると、
ξ=0.001
和,vecn = サンプル数依存性(ξ,10000)
解析解= ξ*sqrt(π)
plot(vecn,和/解析解)
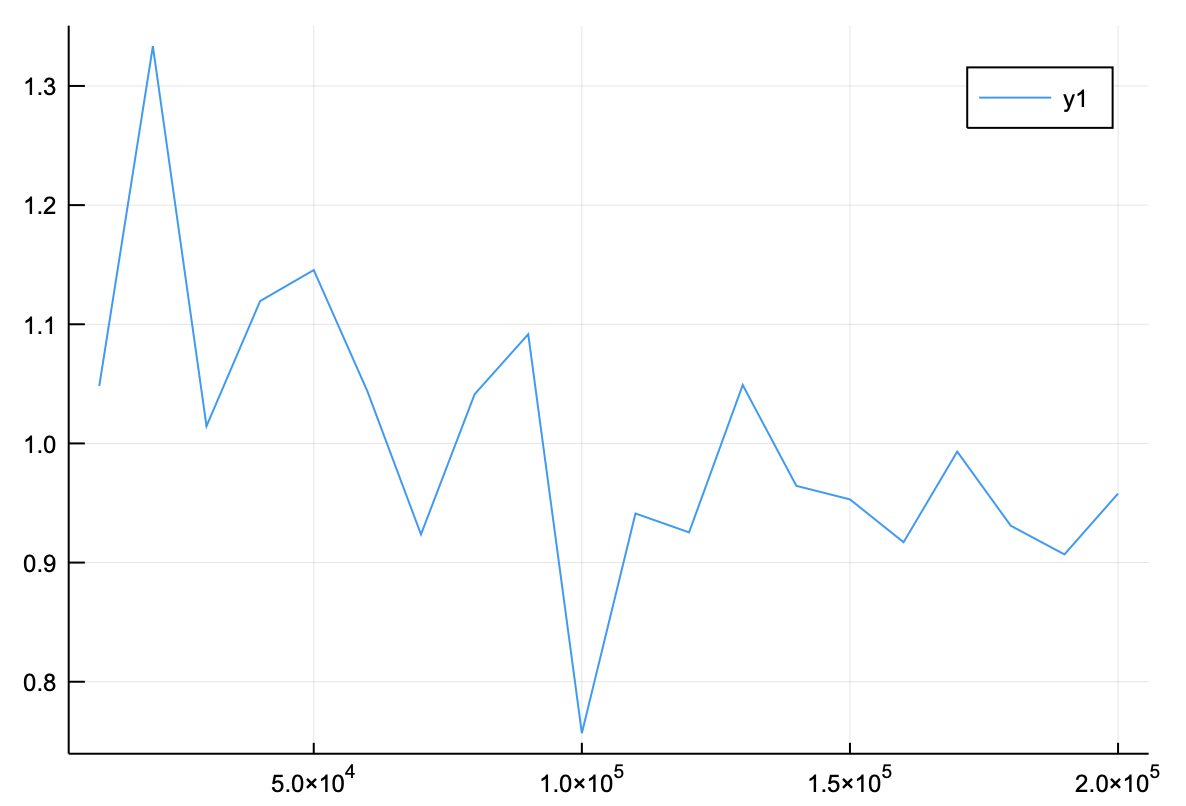
全然ダメである。
重みつきモンテカルロ法
上でやったモンテカルロ法がよくないのは、関数が原点付近に局在しているにもかかわらず、$x_i$を適当に生成させて和を取ったからである。
これを改善するために、乱数を偏らせるのはどうだろうか。つまり、本当にランダムに$x_i$をとるのではなく、ある確率分布$P(x_i)$に従って
$x_i$を生成させることを考える。
積分
$$
I = \int_{-\infty}^{\infty} dx e^{-x^2/\xi^2}
$$
を
$$
I = \int_{-\infty}^{\infty} dx P(x) \frac{e^{-x^2/\xi^2}}{P(x)}
$$
として、変数$x_i$の確率分布を$P(x_i)$として、つまり、$x_i$は確率$P(x_i)$で出現するとして、計算することにする。
つまり、積分を
$$
I \sim \frac{1}{n}\sum_{i=1}^n \frac{e^{-x_i^2/\xi^2}}{P(x_i)}
$$
と近似する。$P(x)$は確率分布なので、
$$
\int_{-\infty}^{\infty} dx P(x) = 1
$$
となるように規格化しておく。
Juliaでは、好きな乱数分布を取ることができる。これは、
using Distributions
を使えば実現できる(もし入っていなければ、]を押してパッケージモードにしてからadd Distributionsを行う)。例えば、平均0、分散0.01の正規分布は
x = range(-1,1,length=100)
m = Normal(0,0.01)
f(x) = pdf(m,x)
I = 積分(100,f,-1,1)
println(I)
plot(x,f)
0.9841320345809936
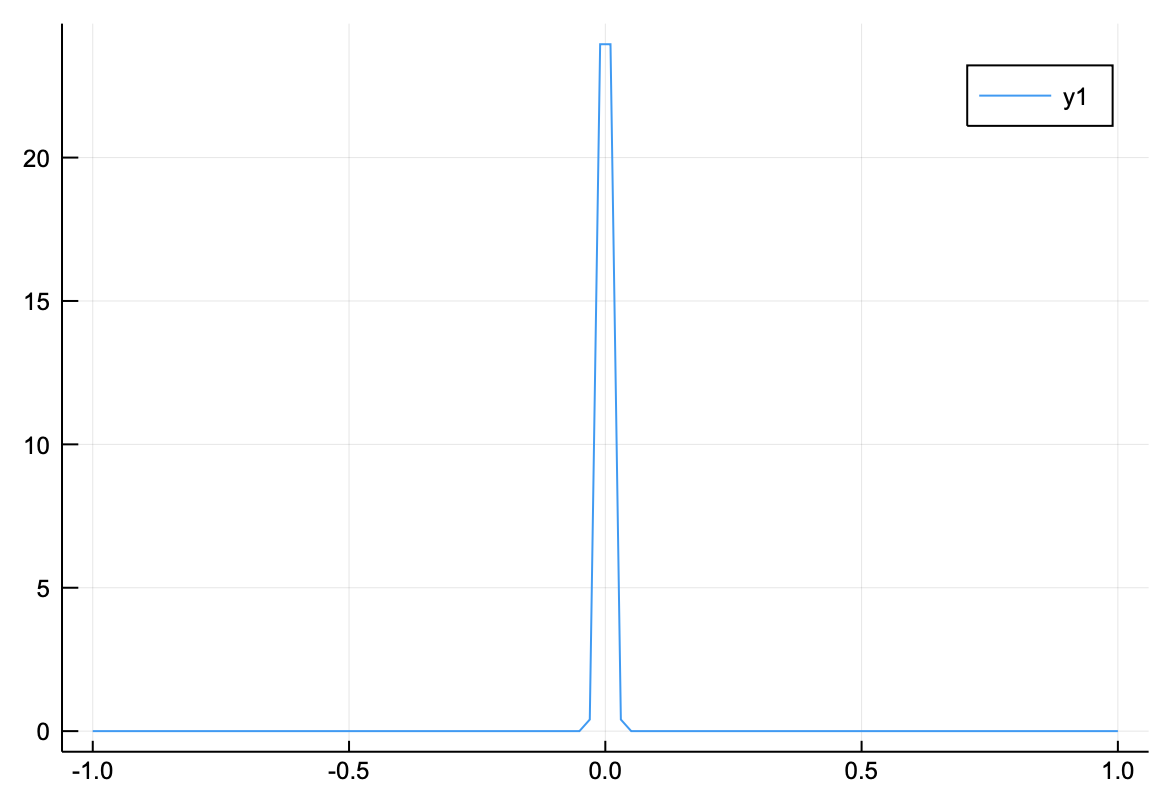
となる。よって、
function 重みつきモンテカルロ積分(n,f,xmin,xmax,m)
和 = 0.0
for i in 1:n
xi = rand(m)
和 += f(xi)/pdf(m,xi)
end
和 = 和/n
return 和
end
これを使って、重みとして正規分布を使った場合と、単純なモンテカルロ法を使った場合と、数値積分した結果の三つを比較してみよう。
function 重みつきのサンプル数依存性(ξ,dn,m)
和 = zeros(Float64,20)
xmin = -10.0
xmax = 10.0
f(x) = exp(-x^2/ξ^2)
vecn = Int64[]
for i in 1:20
n = i*dn
和[i] = 重みつきモンテカルロ積分(n,f,xmin,xmax,m)
push!(vecn,n)
end
return 和,vecn
end
m = Normal(0,0.01)
ξ=0.01
n = 30
和1,vecn = 重みつきのサンプル数依存性(ξ,n,m)
和2,vecn = サンプル数依存性(ξ,n)
和3,vecn = 刻み幅依存性(ξ,n)
解析解 = ξ*sqrt(π)
plot(vecn,[和1/解析解,和2/解析解,和3/解析解],label=["Normal distribution","Uniform distribution","Numerical integration"])
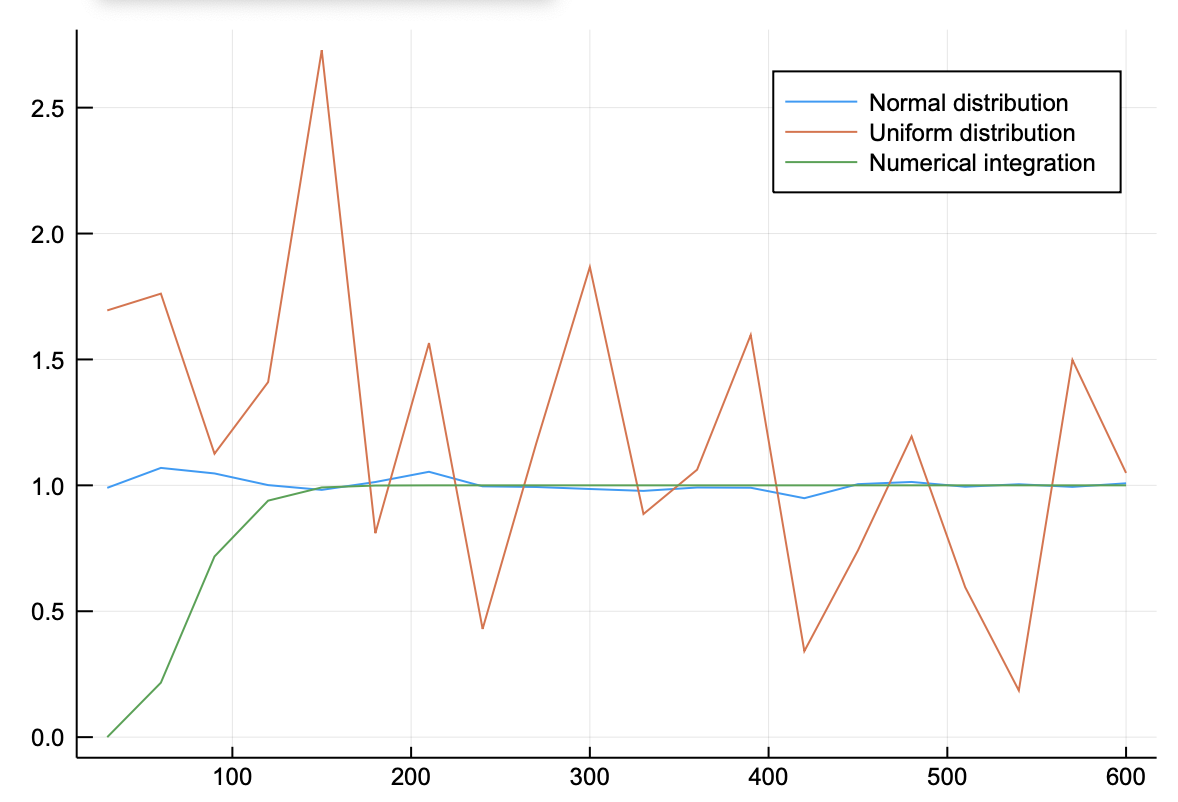
600個取るまでもなく、積分の精度は良い。$\xi=0.001$とすると
m = Normal(0,0.001)
ξ=0.001
n = 30
和1,vecn = 重みつきのサンプル数依存性(ξ,n,m)
和2,vecn = サンプル数依存性(ξ,n)
和3,vecn = 刻み幅依存性(ξ,n)
解析解 = ξ*sqrt(π)
plot(vecn,[和1/解析解,和2/解析解,和3/解析解],label=["Normal distribution","Uniform distribution","Numerical integration"])
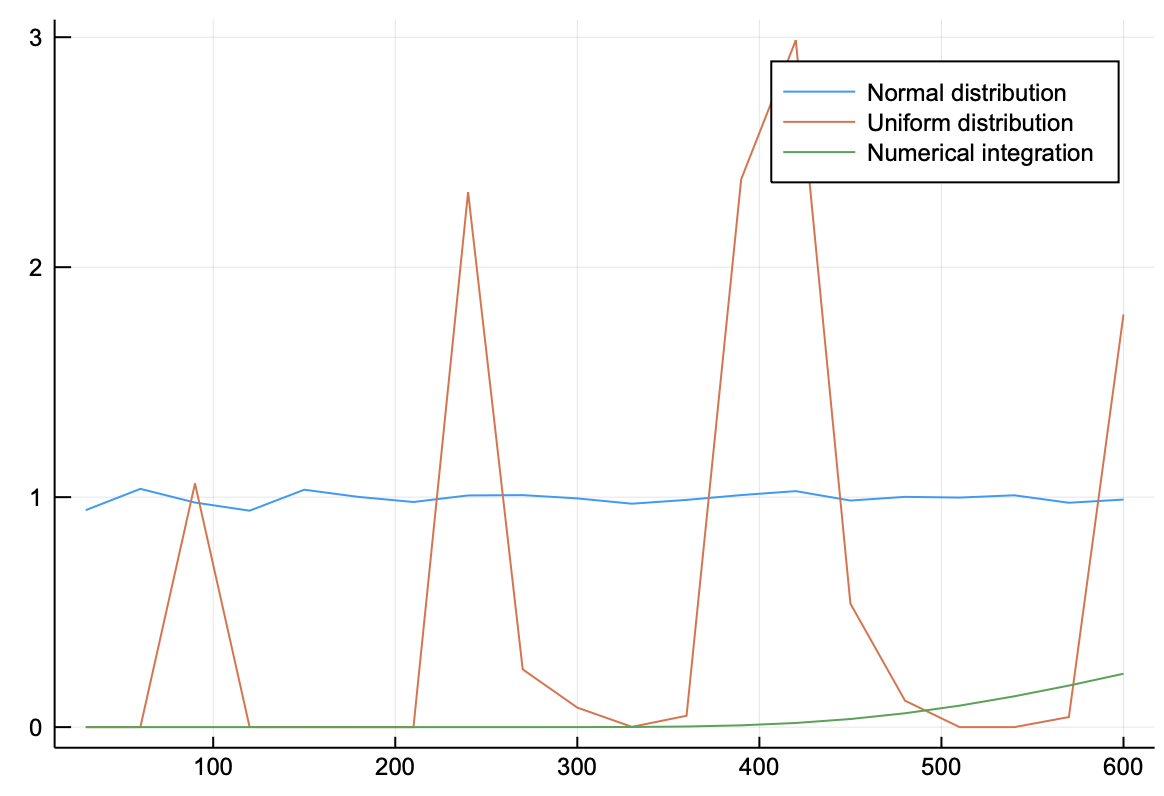
となる。確率分布関数を$\xi$によって変化させているため、重みつきモンテカルロ法は常に良い精度を出す。
次の問題としては、あらかじめ確率分布がわかっていない場合に、どのように計算するか、である。次回以降では、マルコフ連鎖モンテカルロ法を使って計算してみる。