水素原子に対するSchrödinger方程式を実空間差分法で数値的に解いてみる

@dc1394 さんの記事
水素原子に対するSchrödinger方程式を有限要素法で数値的に解いてみる（C++とJuliaのソースコード付き）
にインスパイアされて、実空間差分法でJuliaで解いてみることにしました。

Juliaのバージョン

Julia 1.5.3

解くべき微分方程式

解くべき微分方程式は水素原子に対するSchrödinger方程式で、

\left(-\frac{1}{2} \frac{d^2}{dr^2}-\frac{1}{r}\frac{d}{dr} -\frac{1}{r} \right) \psi(r) = E \psi(r)

という動径座標の微分方程式を解きます。境界条件は

\psi(r_c) = 0

とします。

微分演算子の差分化

さて、微分演算子を差分化します。

$f(r_i+a)$と$f(r_i-a)$の$r_i$まわりのテイラー展開：

f(r_i+a) = f(r_i) + \frac{df}{dr}|_{r = r_i}  a + \frac{1}{2} \frac{d^2f}{dr^2}|_{r = r_i}  a^2 +\cdots

f(r_i-a) = f(r_i) -\frac{df}{dr}|_{r=r_i}  a + \frac{1}{2} \frac{d^2f}{dr^2}|_{r = r_i}   a^2 + \cdots

から、一階微分は

\frac{df}{dr}|_{r = r_i} = \frac{f(r_i+a) -f(r_i-a) }{2a}

となり、二階微分は

\frac{d^2f}{dr^2}|_{r = r_i} = \frac{f(r_i+a) -2f(r_o)+ f(r_i-a)}{a^2}

となります。

空間の差分化は$i = 1,2,\cdots,N$として、

r_i = a i - \frac{a}{2}

とします。系の半径は$R = aN$のとします。この時、最初の点の座標は$r_1 = a/2$、最後の点の座標は$r_N = a N -a/2$となります。さて、$i=1$のとき、一階微分は

\frac{df}{dr}|_{r = a/2} = \frac{f(3a/2) -f(-a/2) }{2a}

となりますが、$f(-a/2)$は未定義です。しかし、$r<0$の領域は回転対称性があるので$r$と同じ値になるはずです。つまり、$f(-a/2)=f(a/2)$ですね。
$i = N$の時、$f(a N + a/2)$の値が必要になります。いま、ディスク状の領域を考えているため、$r>R$での解はゼロであるとすると、$f(aN+a/2)=0$とおくことができます。
一階微分と二階微分を

\frac{df}{dr}|_{r = r_i} = \sum_j c_{ij} f(r_j)

\frac{d^2f}{dr^2}|_{r = r_i} = \sum_j d_{ij} f(r_j)

を書くとしますと、
係数$c_{ij}$と$d_{ij}$は、$i=1$のとき
$$
c_{1j} = \frac{1}{2a} \left[ \delta_{2j} - \delta_{1j} \right]
$$
$$
d_{1j} = \frac{1}{a^2} \left[ \delta_{2j} - 2\delta_{1j}+ \delta_{1j} \right]
$$
となり、$i=N$のとき
$$
c_{Nj} = \frac{1}{2a} \left[ - \delta_{N-1 j} \right]
$$
$$
d_{Nj} = \frac{1}{a^2} \left[ - 2\delta_{N j}+ \delta_{N-1 j} \right]
$$
となり、それ以外のとき
$$
c_{ij} = \frac{1}{2a} \left[ \delta_{i+1 j} - \delta_{i-1 j} \right]
$$
$$
d_{ij} = \frac{1}{a^2} \left[ \delta_{i+1 j} - 2\delta_{i j}+ \delta_{i-1 j} \right]
$$
となります。

これを実装しますと

function calc_cij(i,j,a,N)
    cij = 0.0
    if i==1
        cij = ifelse(j==2,1.0,0.0)        
        cij += ifelse(j==1,-1.0,0.0)
    elseif i==N
        cij = ifelse(j==N-1,-1.0,0.0)
    else
        cij = ifelse(j==i+1,1.0,0.0)
        cij += ifelse(j==i-1,-1.0,0.0)
    end
    cij = cij/(2a)
    return cij
end
    
function calc_dij(i,j,a,N)
    dij = 0.0
    if i==1
        dij += ifelse(j==2,1.0,0.0)
        dij += ifelse(j==1,-1.0,0.0) #-2+1
    elseif i==N
        dij += ifelse(j==N,-2.0,0.0)        
        dij += ifelse(j==N-1,1.0,0.0)
    else
        dij += ifelse(j==i+1,1.0,0.0)
        dij += ifelse(j==i,-2.0,0.0)
        dij += ifelse(j==i-1,1.0,0.0)
    end
    dij = dij/(a^2)
    return dij
end

となります。

行列の作成

これで微分演算子を差分化できましたので、ハミルトニアン行列は

function make_Hr(a,N,n)
    mat_Hr = zeros(Float64,N,N)
    for i in 1:N
        r = a*i -a/2
        mat_Hr[i,i] = -1/r
        for dr in -1:1
            j = i + dr
            if 1 <= j <= N
                cij = calc_cij(i,j,a,N)
                dij = calc_dij(i,j,a,N)
                mat_Hr[i,j] += -(dij/2 + cij/r)
            end
        end
    end
    return mat_Hr
end

となります。
結果を見るためのコードは

using LinearAlgebra 
using Plots
N = 1000
rc = 30
rcs = [30,60,120]
nmax = 10
for i = 1:length(rcs)
    rc = rcs[i]
    a = rc/N
    n = 0
    mat_Hr = make_Hr(a,N,n)

    ε,ψ = eigen(mat_Hr)
    ε = sort(ε)
    if i==1
        plot(ε[1:nmax],label="rc = $rc")
    else
        plot!(ε[1:nmax],label="rc = $rc")
    end
    
end
savefig("eigen.png")

です。

結果

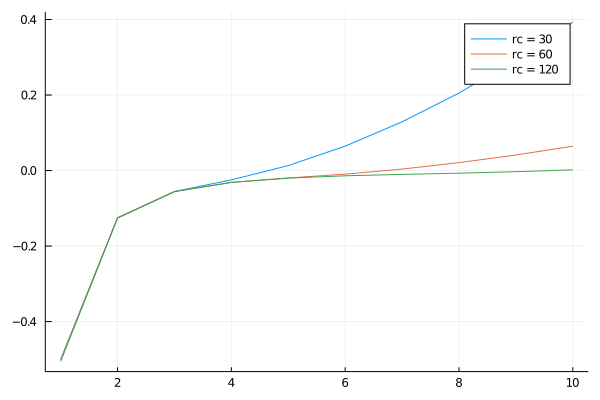
得られた結果は

です。
@dc1394 さんの記事
水素原子に対するSchrödinger方程式を有限要素法で数値的に解いてみる（C++とJuliaのソースコード付き）
の厳密解と比較してみると、rc=120なら良さそうです。