自動微分を使って量子力学の逆問題を解いてみる
量子力学の問題を解く時、通常、あるポテンシャルがある時の電子の状態を求めます。一方、何らかの実験などで電子密度だけ求まっているときに、その電子密度を出すようなポテンシャルを求めることは可能でしょうか? ホーヘンベルク・コーンの定理によれば、「ある系の基底状態の電子密度ρが決まると、それを基底状態にもつ外部ポテンシャルがもし存在すれば(v-表示可能性の仮定)それはただ1通りに定まる。」だそうです。ということは、相互作用のない簡単な系であれば、計算で確かめられるかもしれません。
Juliaで自動微分を使って、1次元の簡単な系についてやってみましょう。
相互作用のないN電子系
時間依存しない1次元系を考えます。量子力学の従う1電子はシュレーディンガー方程式
\left[ -\frac{\hbar^2}{2m} \frac{d^2}{d x^2} + V(x) \right] \psi_n(x) = \epsilon_n \psi_n(x)
を解くことで振る舞いを知ることができます。$N$個の相互作用しない電子の場合には、
\sum_{k=1}^N \left[- \frac{\hbar^2}{2m} \frac{d^2}{d x_k^2} + V(x_k) \right] \Psi_n(x_1,\cdots,x_N) = E_n \Psi_n(x_1,\cdots,x_N)
となりますが、$\Psi_n$は$\psi_{n_1}(x_1) \cdots \psi_{n_N}(x_N)$の線型結合が解です。また、固有値は$E_n = \sum_{i}^N \epsilon_{n_i}$となります。こちらで述べましたように、電子はフェルミオンですから、基底状態のエネルギーは$\epsilon_1 < \epsilon_2 < \cdots < \epsilon_N$となるエネルギーを用いて
E_0 = \sum_{i=1}^N \epsilon_{i}
と書けます。この時、電子密度は
\rho(x) = \sum_{i=1}^N |\psi_i(x)|^2
となります。
問題設定
電子密度$\rho(x)$だけわかっている時に、ポテンシャル$V(x)$を決定できるでしょうか?
通常は、
「ポテンシャル$V(x)$を決める」 -> 「シュレーディンガー方程式を解く」 -> 「電子密度$\rho(x)$を求める」
という流れですが、
「電子密度$\rho(x)$を知っている」 -> 「計算した結果$\rho(x)$となるようなポテンシャル$V(x)$を求める」
をしたいわけです。逆問題ですね。
例えば、
こんな電子密度を持つような$V(x)$を求められるでしょうか。
問題の整理
簡単のために、1次元系を離散化してしまいましょう。長さ$L$の系を$M$点で離散化すると、2階微分は
\frac{d^2 \psi(x)}{d x^2} \Big|_{x = x_i} \sim \frac{1}{(\Delta x)^2} (\psi(x_{i+1}) - 2 \psi(x_i) + \psi(x_{i-1}))
となりますから、1粒子のシュレーディンガー方程式は
H(\vec{V}) \vec{\psi}_n = \epsilon_n \vec{\psi}_n
という固有値問題となります。行列が$\vec{V}$に依存していますから、固有ベクトル$\vec{\psi}_n$も$\vec{V}$に依存しており、電子密度も
\vec{\rho}_{\vec{V}} = \sum_{n=1}^N |\vec{\psi}_n(\vec{V})|^2
と$\vec{V}$に依存しています。
そして、問題は、ある電子密度$\vec{\rho}$が与えられた時、loss関数:
{\cal L}(\vec{V}) = \sum_{k=1}^{M} |[\vec{\rho}]_k - [\vec{\rho}_{\vec{V}}]_k |^2
が最小となるような$\vec{V}$を求める問題に帰着されます。
自動微分
${\cal L}(\vec{V})$を計算するためには、行列の固有値問題を解く必要があります。つまり、${\cal L}(\vec{V})$を最小化するために$\partial {\cal L}(\vec{V})/\partial \vec{V}$を計算したければ、固有ベクトルの微分を計算しなければなりません。通常のよくあるような関数であれば微分は自動微分で簡単にできそうですが、計算が複雑そうな固有値問題においても自動微分はできるのでしょうか?
結論から言うと、可能です。例えば、こちらを参照してみてください(英語)。
JuliaではZygoteを使って簡単に微分が計算できますから、問題なく${\cal L}(\vec{V})$を最小化できます。
コード
行列の作成と電子密度の計算
ハミルトニアンとポテンシャルを使って電子密度を計算するには、
using LinearAlgebra
using Optim
using Zygote
using Plots
function make_H(N,L)
Δx = L/(N+1)
H = zeros(Float64,N,N)
for i=1:N
x = i*Δx
j = i+1
dij = -1/Δx^2
if 1 ≤ j ≤ N
H[i,j] += dij
end
j=i
dij = 2/Δx^2
if 1 ≤ j ≤ N
H[i,j] += dij
end
j=i-1
dij = -1/Δx^2
if 1 ≤ j ≤ N
H[i,j] += dij
end
end
return H
end
function calc_rho(H0,V,numstates)
N,_ = size(H0)
H = H0 + Diagonal(V)
e,v = eigen(H)
rho_n = zeros(N)
for n=1:numstates
rho_n += abs.(v[:,n]).^2
end
return rho_n
end
という関数を使います。
最適化
最適なポテンシャルを用いるにはOptim.jlを用います。また、loss関数の微分はZygote.jlを用います。
function main()
L = 1
N = 100
xs = range(0,L,length=N)
Vamp = 100
xi = 0.1
V = sin.(π*xs/L)+exp.(-(xs.-L/4).^2 ./xi^2)+cos.(4*π*xs/L).^2
V *= Vamp
numstates = 10
H0 = make_H(N,L)
rho_output = calc_rho(H0,V,numstates)
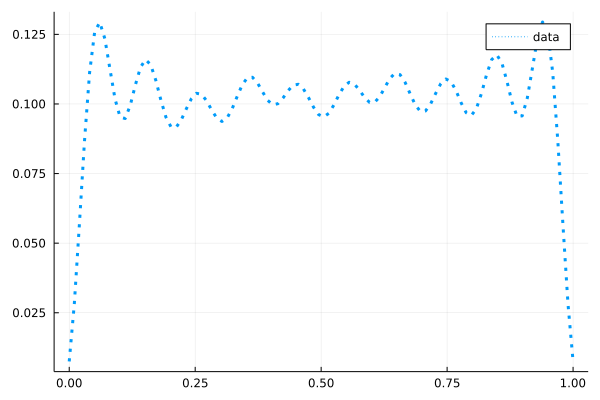
p1 = plot(xs,rho_output,label="data",lw=3, ls=:dot)
savefig(p1,"rho_output.png")
function loss(V)
rho = calc_rho(H0,V,numstates)
return sum(abs.(rho-rho_output))
end
function dlossdV!(G,V)
G .= loss'(V)
end
Vini = rand(N)
results = optimize(loss, dlossdV!, Vini, iterations=100000)
println("minimum = $(results.minimum) with in "*
"$(results.iterations) iterations")
show(results)
Vr = Optim.minimizer(results)
rho_estimated = calc_rho(H0,Vr,numstates)
Vr0 = Vr[N ÷ 2]
V0 = V[N ÷ 2]
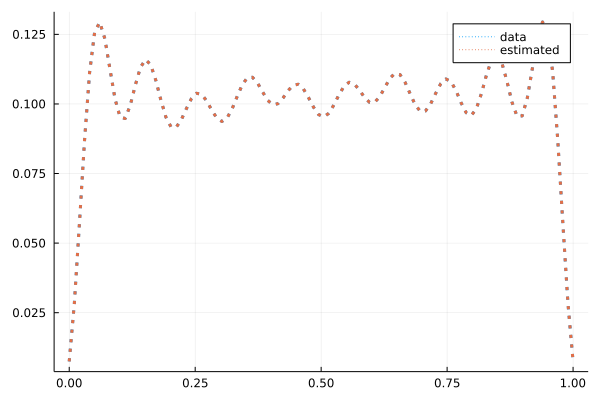
plot!(p1,xs,rho_estimated,label="estimated",lw=3, ls=:dot)
savefig(p1,"rho_estimated.png")
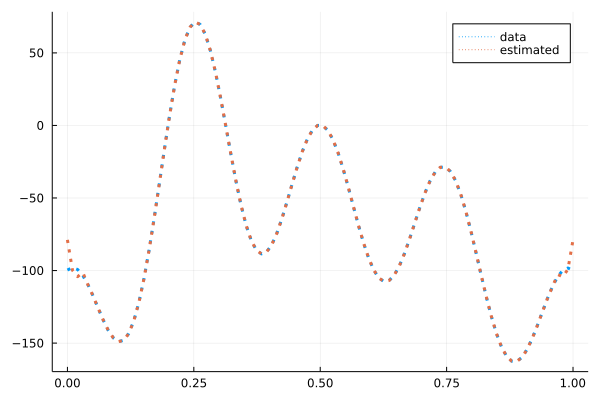
p2 = plot(xs,V .- V0,label="data",lw=3, ls=:dot)
plot!(p2,xs,Vr .- Vr0,label="estimated",lw=3, ls=:dot)
savefig(p2,"potential.png")
end
main()
結果
得られた結果を示します。得られた電子密度は
となりました。電子密度はほぼ完全に再現しています。
その時のポテンシャルは
となります。端の部分以外はバッチリ合っていますね。