5次元超格子を2次元平面に射影してペンローズタイル準結晶を作ってみよう in Juliaの続編です。
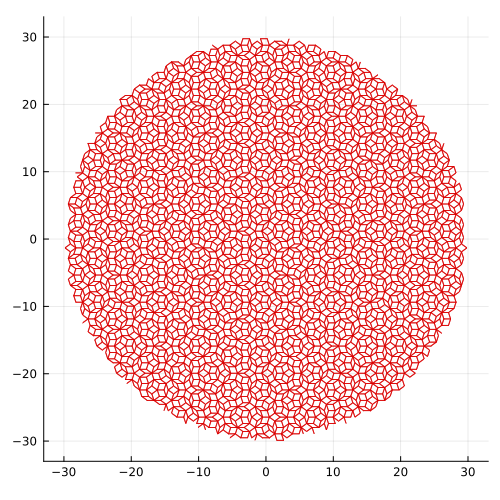
適当な形のいくつかのタイリングを空間に敷き詰めるとき、周期的に並ぶ場合とそうじゃない場合があります。有名なものはペンローズタイルです(下図)。
このペンローズタイルは、太い菱形と細い菱形からできています。また、図をよくよく見ると、太い菱形の向きは5通り、細い菱形の向きは5通りあり、全部で10種類の菱形からできています。
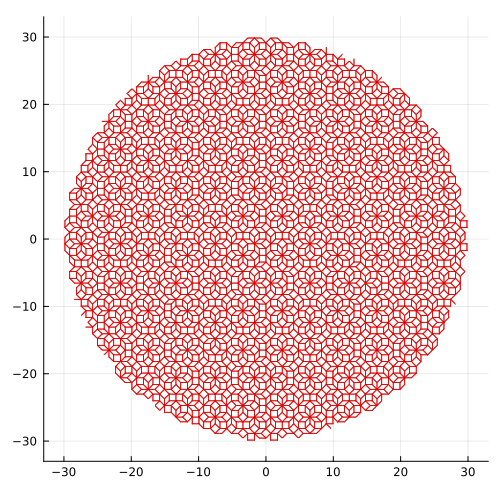
また、準周期タイリングの有名なものととして、 Ammann–Beenkerタイルがあります(下図)。
これは、正方形と菱形からできています。図をよく見ると、正方形は、正方形が45度傾いているものと合わせて2つ、菱形は横になっているものが2つ、縦になっているものが2つで、全部で6種類あります。
ペンローズタイルの10種類の10、Ammann–Beenkerタイルの6種類の6という数字はどこから来ているのでしょうか?
実は、ペンローズタイルは5次元の超格子の2次元への射影、Ammann–Beenkerタイルは4次元の超格子の2次元への射影から作られているという事実から来ているのです。これについてみていきましょう。
そして、この事実を用いることで効率的に準周期タイルを求めるDual-Grid法について説明し、そのアルゴリズムをJuliaで実装してみます。なお、上の二つの図形は後半で述べるコードから生成されたものです。
N次元超格子とタイルの種類
N次元超格子
まず、N次元の超格子を定義します。N次元空間に互いに直交するN本のベクトル$\vec{A}_i$を用意します。このN本のベクトルを使って格子点の座標を定義するには、
R = K_0 \vec{A}_0 + \cdots K_{N-1} \vec{A}_{N-1}
とします。ここで、$K_{0},\cdots,K_{N-1}$はN個の整数で、
\vec{K}^T = (K_0,K_2,K_3,\cdots,K_{N-1})
となっています。
一つの格子点$\vec{K}$を考えます。N次元空間中で、この格子点の隣の点は、例えば、
\vec{K}_1^T = (K_{0}-1,K_1,K_2,\cdots,K_{N-1})
や
\vec{K}_2^T = (K_{0},K_1-1,K_2,\cdots,K_{N-1})
などがあります。考えた格子点と隣の点を全部で4つ見つけてきて線を結んでみます。すると、当然それはN次元空間中の2次元の正方形となります。例えば、
\vec{K}_0^T = (K_{0},K_1,K_2,\cdots,K_{N-1})\\
\vec{K}_1^T = (K_{0}-1,K_1,K_2,\cdots,K_{N-1}) \\
\vec{K}_2^T = (K_{0},K_1-1,K_2,\cdots,K_{N-1}) \\
\vec{K}_3^T = (K_{0}-1,K_1-1,K_2,\cdots,K_{N-1})
という4点を選んできて線を結ぶと、正方形になります。これは、1番めと2番めの軸を動かして得られた正方形ですが、N本の軸のどれか2つを選べばそれぞれ異なる方向を向いた正方形が得られます。
物理空間への射影
さて、このN次元空間中に、2次元平面を用意します。この2次元平面の座標を$x,y$とした時、
(x,y,0,0,\dots)
というものを2次元平面とします。つまり、N次元空間中の1番めと2番めの座標以外は0とすることで、平面を定義します。
この平面を「物理空間」と呼ぶことにします。
さて、先ほど超格子で作った正方形を、この2次元平面に射影することを考えます。正方形を作る4点を平面に射影するわけですから、射影されたものは四角形です。ただし、超格子が2次元平面に対してどのように傾いているかによって、その四角形の形状は変わるでしょう。正方形を作るにあたって、N次元中の超格子の軸の選び方はいくつかあり、それによって正方形の向きは変わります。ですので、射影された四角形の形状は当然変わります。ただし、軸を選びさえすれば、どの座標であってもいつも同じ形です。
つまり、N本の軸から2つの軸を選んできて得られる正方形の数の分だけ、射影された空間に四角形が現れます。つまり、組み合わせ$N!/(2!(N-2)!)$です。そして、5次元であれば10、4次元であれば6が得られます。これがペンローズタイルとAmmann–Beenkerタイルのタイルの種類となっているわけですね。
物理空間でのタイル
N次元空間の超格子から作った正方形が二次元の物理空間に射影されることでタイルになることはわかりました。次は、自分が作りたいタイルができるようにN次元超格子を設定しましょう。N次元超格子は$\vec{A}_i$というN本のベクトルによって定義されています。正方形をなす4つの点は超格子の点ですから、N本のベクトルがどのように物理空間に射影されているかが分かればタイルの形状がわかることになります。物理空間へ射影するためには、単純にN次元ベクトルの3番め以降の値をゼロにします。つまり、
\vec{A}_i = \left( \begin{matrix}
A_{1i} \\
A_{2i} \\
\vdots \\
A_{Ni}
\end{matrix} \right) \rightarrow \left( \begin{matrix}
A_{1i} \\
A_{2i}
\end{matrix} \right) \equiv \vec{a}_i
という射影を行います。ここで、小文字のベクトル$\vec{a}$は2次元のベクトルとします。超格子から作った正方形を構成する4点は、この射影によって
\vec{r}_{\rm 2D}^{l} = \sum_{j=0}^{N-1} K_{j}^l \left( \begin{matrix}
A_{1i} \\
A_{2i}
\end{matrix} \right)
という2次元のベクトルとなります。ここで、$l=0,\cdots,3$は正方形をなす点を区別するインデックスです。正方形の線分を表すベクトルは2つのベクトルの差を取ればいいので、
\vec{r}_{\rm 2D}^{0} - \vec{r}_{\rm 2D}^{1} = \left( \begin{matrix}
A_{1n} \\
A_{2n}
\end{matrix} \right) \\
\vec{r}_{\rm 2D}^{0} - \vec{r}_{\rm 2D}^{2} = \left( \begin{matrix}
A_{1m} \\
A_{2m}
\end{matrix} \right)
となります。ここで、$n$,$m$は正方形を作るためにとった$m$本目及び$n$本目の軸とします。この二つのベクトルから作られる平行四辺形が、タイリングのタイルとなります。
さて、ペンローズタイルの場合は太い菱形と細い菱形の組み合わせでできています。これらの菱形を構成する線分は、5本の星型のベクトル$\vec{d}_j (j = 0,\cdots,4)$:
\vec{d}_j = \left( \begin{matrix}
\cos j \theta \\
\sin j \theta
\end{matrix} \right)
に平行です。ここで、$\theta = 2\pi/5$です。これら5本のベクトルが5次元空間の超格子を示す5本のベクトルの射影になっていればいいということですから、
\vec{A}_j = \left( \begin{matrix}
\cos j \theta \\
\sin j \theta \\
A_{3j} \\
A_{4j} \\
A_{5j}
\end{matrix} \right)
のような形のベクトルになっていれば、ペンローズタイルのタイルを構成できます。文献によれば、
\vec{A}_j = \sqrt{\frac{2}{5}}\left( \begin{matrix}
\cos j \theta \\
\sin j \theta \\
\cos 2j \theta \\
\sin 2j \theta \\
1/\sqrt{2}
\end{matrix} \right)
とすると、ペンローズタイルを作ることができて、長さが1で互いに直交するベクトルとなるそうです。ただし、$\sqrt{2/5}$が掛かっているために、2次元に射影した時の線分の長さは1ではなくなっていますので注意してください。なお、最初の2成分はタイルのベクトルを決めるものですが、残りの3成分を自由に決めてもタイルを構成する2次元ベクトルに影響がありません。この残りの3成分をうまく決めると、準周期系ではなく、様々な周期を持つ周期系にすることができます。
N次元超格子の超平面と2次元物理空間の断面
物理平面として$(x,y,0,\cdots,0)$を考えましたが、超格子の全ての格子点を射影してしまうと個数は無限個あるわけですからタイルにはなりません。そのため、射影する超格子の点を選ぶ必要があります。一番単純な方法は、N次元超格子と2次元物理空間が交わった場所の近辺の格子点をとってくることです(格子点がちょうど物理平面上にあることもありますが、そうではないことの方が多いでしょう)。高次元空間をイメージすることは難しいので、3次元空間で考えてみることにします。
まず、物理空間を地面として、それに対して超格子は斜めになっているわけです。ですので、ピサの斜塔のように斜めに立った塔を思い浮かべてください。この塔の$K_0$階に立っているとします。もちろん、斜めに傾いています。この時、この階の床に平行な面を考え、それを塔の外にどこまでも広げていくとします。塔の外に広げていくと、最後には地面に刺さります。2次元の平面に対して刺さっていますので、この断面は1次元の直線です。
この平行な面を超平面と呼ぶと、超平面を表す式は
(K_0 + s_0) \vec{A}_0 + \sum_{j=1}^{N-1} (\theta_{j}+s_j) \vec{A}_j
となります。ここで、$\theta_{j}$は実数で、5次元空間であれば、4つのパラメータとなります。つまり、N次元空間の一つのベクトルを固定して、残りのベクトルを自由に動かしているわけです。3次元空間であれば、まさにこれは斜塔の床に平行な面になっていますね。また、$s_0$は斜塔の床を少しだけ嵩上げするために導入されたパラメータです。この超平面は、$\vec{A}_0$に垂直な平面です。言い換えれば、$\theta_j$をいくら動かしても、超平面上の点の$\vec{A}_0$成分は常に$(K_0 + s_0)$で変化しません。$s_j$はそれぞれの軸を少しシフトするもので、このシフトの仕方によって得られるタイリングパターンが変化します。
次に、物理空間$(x,y,0,\cdots,0)$とこの超平面の断面を考えます。$\theta_j$をいくら動かしても$\vec{A}_0$成分が変わらないのであれば、断面を表す直線のどこであっても常に$\vec{A}_0$が変わらないことを意味しています。さらに、超平面は$\vec{A}_0$に垂直ですので、物理空間上の断面を表す直線も$\vec{A}_0$に垂直になっているはずです。物理空間における直線の式を
\alpha \left( \begin{matrix}
\vec{a}_0 \\
0 \\
\vdots \\
0
\end{matrix} \right)+ \theta_0 \left( \begin{matrix}
\vec{a}_0^{\perp} \\
0 \\
\vdots \\
0
\end{matrix} \right)
とおきます。ここで、$\vec{a}_0$は$\vec{A}_0$を物理空間に射影したもので、すでに上で定義しています。$\vec{a}_0^{\perp}$は$\vec{a}_0$に垂直なベクトルです。$\theta_0$が実数で、これを動かすことで$\vec{a}_0$に垂直な直線を考えることができます。超平面と物理空間の断面を考えるので、二つの式が同時に成り立つ必要があり、
(K_0 + s_0) \vec{A}_0 + \sum_{j=1}^{N-1} (\theta_{j}+s_j) \vec{A}_j = \alpha \left( \begin{matrix}
\vec{a}_0 \\
0 \\
\vdots \\
0
\end{matrix} \right)+ \theta_0 \left( \begin{matrix}
\vec{a}_0^{\perp} \\
0 \\
\vdots \\
0
\end{matrix} \right)
となるような$\alpha$を求めればよいわけです。ここで、左から$\vec{A}_0^T$をかけると、
K_0 + s_0 = \alpha \vec{a}_0^T \vec{a}_0
となるので、
\alpha = \frac{1}{\vec{a}_0^T \vec{a}_0}(K_0 + s_0)
となります。
断面同士の交点
超平面と物理空間の断面は直線になりました。超平面を定義するときに超格子の一つの軸を選んで一つの整数($K_0$など)を選んでいましたから、物理空間との断面において、一つの整数が決まっています。元々、超格子の点を4つ選んで正方形を作ってタイルを作成することを考えれば、整数をもう一つ選ぶことができれば、
\vec{K}_0^T = (K_{0},K_1,K_2,\cdots,K_{N-1})\\
\vec{K}_1^T = (K_{0}-1,K_1,K_2,\cdots,K_{N-1}) \\
\vec{K}_2^T = (K_{0},K_1-1,K_2,\cdots,K_{N-1}) \\
\vec{K}_3^T = (K_{0}-1,K_1-1,K_2,\cdots,K_{N-1})
という4つの格子点を選ぶことができます。ということで、超平面をもう一つ用意します。今後は先ほど選んだ軸と異なる軸です。2番めの軸を選んで整数を$K_1$と決めたとすると、超平面と物理空間との断面は先ほどと同じように
\left( \begin{matrix}
\vec{r} \\
0 \\
\vdots \\
0
\end{matrix} \right) =
\frac{1}{\vec{a}_1^T \vec{a}_1}(K_1 + s_1) \left( \begin{matrix}
\vec{a}_1 \\
0 \\
\vdots \\
0
\end{matrix} \right)+ \theta_1 \left( \begin{matrix}
\vec{a}_1^{\perp} \\
0 \\
\vdots \\
0
\end{matrix} \right)
となります。ここで、$\vec{r}$は直線上の点です。
この断面と先ほどの断面の交点は
\frac{1}{\vec{a}_1^T \vec{a}_1}(K_1 + s_1)
\vec{a}_1 + \theta_1
\vec{a}_1^{\perp} = \frac{1}{\vec{a}_0^T \vec{a}_0}(K_0 + s_0)
\vec{a}_0
+ \theta_0
\vec{a}_0^{\perp}
となり、$\theta_0$と$\theta_1$が決まります。具体的には、
\left( \begin{matrix}
\vec{a}_0^{\perp} &
-\vec{a}_1^{\perp}
\end{matrix} \right)
\left( \begin{matrix}
\theta_0 \\
\theta_1
\end{matrix} \right) = \frac{1}{\vec{a}_1^T \vec{a}_1}(K_1 + s_1)
\vec{a}_1 -\frac{1}{\vec{a}_0^T \vec{a}_0}(K_0 + s_0)
\vec{a}_0
とすると、$\theta_0$と$\theta_1$に関する連立方程式になっていますので、、$\theta_0$と$\theta_1$を求めることができます。その結果、交点の座標$\vec{r}^T = (x,y)$が求まります。
物理空間に一番近い超格子
断面同士の交点を求めたので、その交点においては、二つの整数(自分で選んだ二つの軸に関する整数。$K_0$や$K_1$など)が決まっています。そして、この交点は超平面の上の点です。つまり、
\left( \begin{matrix}
\vec{r} \\
0 \\
\vdots \\
0
\end{matrix} \right) = (K_0 + s_0) \vec{A}_0 + (K_1 + s_1) \vec{A}_1+ \sum_{j=2}^{N-1} (\theta_{j}+s_j) \vec{A}_j \equiv \vec{R}
という式が成り立ちます。そして、超格子のベクトルがそれぞれ直交することを利用すれば、$\theta_j$は
\theta_j + s_j=
\vec{A}_j^T \vec{R}
と求めることができます。$\theta_j$は通常実数ですので、この交点は超格子の格子点上にはありません。従って、一番近い格子点を見つける必要があります。そこで、
K_j = [\theta_j]
とします。ここで、$[]$はガウス記号です。つまり、それを超えない最大の整数となります。4.4なら4、3.2なら3、-2.1なら-2、-1.9なら-1です。これで、格子点の座標$K_0,\cdots,K_{N-1}$を見つけることができました。あとは、
\vec{K}_0^T = (K_{0},K_1,K_2,\cdots,K_{N-1})\\
\vec{K}_1^T = (K_{0}-1,K_1,K_2,\cdots,K_{N-1}) \\
\vec{K}_2^T = (K_{0},K_1-1,K_2,\cdots,K_{N-1}) \\
\vec{K}_3^T = (K_{0}-1,K_1-1,K_2,\cdots,K_{N-1})
という4点を用意して、物理空間に射影しましょう。
コード
全体のアルゴリズム
準周期タイルの点を求める全体のアルゴリズムは以下の通りです
- N次元の軸から2つの軸を選んだ組み合わせを生成する。$N!/(2!(N-2)!)$通り。これがタイルの種類となる(向きが違うタイルは異なる種類とみなした場合)。
- ある軸の組み合わせを考え、それぞれの軸における整数を2つ決める
- その整数から作られる超平面と物理空間での断面同士の交点を表すベクトル$\vec{R}$を求める
- $\theta_j = \vec{A}_j^T \vec{R} -s_j$を行い、ベクトル$\vec{R}$を各格子ベクトル$\vec{A}_j$の和として表す。
- $K_j = [\theta_j]$として、N個の整数の組を一つ決める。
- 上述したように、N次元空間中の正方形を用意するため、N個の整数の組を4つ用意する。
- 4つの超格子点をそれぞれ物理空間に射影することで、タイルの2次元平面内の座標を入手する
- 2.に戻り、全ての組み合わせに対して、2.-7.を実行する。
コード
それでは、Juliaを使ってタイルを作ってみましょう。アルゴリズムのそれぞれの部分を作成していきます。
組み合わせの作成は、
pairs = []
for i=0:n-1
for j=i+1:n-1
push!(pairs,(i,j))
end
end
でできます。これを
for pair in pairs
i1 = pair[1]
i2 = pair[2]
for k1 = -kmax:kmax
for k2 =-kmax:kmax
のようにすれば組み合わせのループができます。そして、アルゴリズムの2.の整数を選ぶのは、k1とk2というループです。
3.の交点を求める関数を作成します。超平面と物理空間との断面は直線です。二つの超平面がそれぞれ物理空間と断面を作り、それらの交点を求めることになります。
断面を表す直線は、ペンローズの場合には、
\frac{5}{2}(K_j + \gamma_j) \vec{d}_j + \theta_j (\vec{d}_{j+1} - \vec{d}_{j-1})
Ammann–Beenkerの場合には
2 (K_j + \gamma_j) \vec{d}_j + \theta_j \vec{d}_{j+2}
です。ここで、$j = 0,\cdots,N-1$ですが、$j+1$や$j-1$などで範囲を超える場合には周期境界条件を課してインデックスを戻すようにします。つまり、ペンローズでは
i1p = ifelse(i1 == n-1,0,i1 + 1)
i1m = ifelse(i1 == 0,n-1,i1 - 1)
i2p = ifelse(i2 == n-1,0,i2 + 1)
i2m = ifelse(i2 == 0,n-1,i2 - 1)
Ammann–Beenkerでは
i1p = i1 + 2
i1p += ifelse(i1p >= n,-n,0)
i2p = i2 + 2
i2p += ifelse(i2p >= n,-n,0)
です。ペンローズの場合、2次元平面での5つのベクトルは
d(j) = (sqrt(2/5))*[cos(j*Θ),sin(j*Θ)]
Ammann–Beenkerでは
d(j) = (1/sqrt(2))*[cos(j*θAB),sin(j*θAB)]
です。これらを用います。
結局、ペンローズの場合の交点を求める関数は
function find_intersection(n,i1,i2,k1,k2,gamma)
i1p = ifelse(i1 == n-1,0,i1 + 1)
i1m = ifelse(i1 == 0,n-1,i1 - 1)
i2p = ifelse(i2 == n-1,0,i2 + 1)
i2m = ifelse(i2 == 0,n-1,i2 - 1)
dpm1 = d(i1p) .- d(i1m)
dpm2 = d(i2p) .- d(i2m)
M = [dpm1 -dpm2]
b = (5/2)*((k2 + gamma[i2+1])*d(i2) .- (k1 + gamma[i1+1])*d(i1))
θ = M \ b
r = (5/2)*(k1 + gamma[i1+1])*d(i1) + θ[1]*dpm1
return r
end
となります。Ammann–Beenkerでは
function find_intersectionAB(n,i1,i2,k1,k2,gamma,factor)
i1p = i1 + 2
i1p += ifelse(i1p >= n,-n,0)
i2p = i2 + 2
i2p += ifelse(i2p >= n,-n,0)
dpm1 = d(i1p)# .- d(i1m)
dpm2 = d(i2p)# .- d(i2m)
M = [dpm1 -dpm2]
b = (1/factor^2)*((k2 + gamma[i2+1])*d(i2) .- (k1 + gamma[i1+1])*d(i1))
θ = M \ b # solve M*θ = b
r = (1/factor^2)*(k1 + gamma[i1+1])*d(i1) + θ[1]*dpm1
return r
end
です。
残りはそのまま実装すればよいので、全体コードで紹介することにします。
全体コード
以上から、ペンローズタイルの点を見つけるコードは
g1 = 0.1
g2 = 0.7
g3 = -0.98
g4 = 0.43
g5 = -(g1+g2+g3+g4)
const gamma = Float64[g1,g2,g3,g4,g5] #5次元空間中でどの位置に2次元平面を置くかのパラメータ。和がゼロだとペンローズタイルになる。
using LinearAlgebra
using Plots
const Θ = 2π/5
d(j) = (sqrt(2/5))*[cos(j*Θ),sin(j*Θ)] #ペンローズタイルを構成する5本のベクトル
function project(K) #探してきた5次元格子点を2次元平面へ射影する
R2d = zeros(Float64,2)
for j=0:4
R2d .+= (K[j+1]+gamma[j+1])*d(j)
end
return R2d
end
function make_aj()
n = 5
abar = Vector{Vector{Float64}}(undef,n)
for j=0:n-1
ϕj = 2π*j/5
abar[j+1] = sqrt(2/5)*[cos(ϕj),sin(ϕj),cos(2ϕj),sin(2ϕj),sqrt(1/2)]
end
return abar
end
function find_intersection(i1,i2,k1,k2,gamma)
Minv = [
sin(i2*Θ) -sin(i1*Θ)
-cos(i2*Θ) cos(i1*Θ)
] ./sin((i2-i1)*Θ)
r = Minv*[k1-gamma[i1+1],k2-gamma[i2+1]]
return r
end
function find_intersection(n,i1,i2,k1,k2,gamma)
i1p = ifelse(i1 == n-1,0,i1 + 1)
i1m = ifelse(i1 == 0,n-1,i1 - 1)
i2p = ifelse(i2 == n-1,0,i2 + 1)
i2m = ifelse(i2 == 0,n-1,i2 - 1)
dpm1 = d(i1p) .- d(i1m)
dpm2 = d(i2p) .- d(i2m)
#println(dot(d(i1),dpm1))
#println(dot(d(i2),dpm2))
#println(dot(d(i1),d(i1)))
M = [dpm1 -dpm2]
b = (5/2)*((k2 + gamma[i2+1])*d(i2) .- (k1 + gamma[i1+1])*d(i1))
θ = M \ b
r = (5/2)*(k1 + gamma[i1+1])*d(i1) + θ[1]*dpm1
#println(r)
r = (5/2)*(k2 + gamma[i2+1])*d(i2) + θ[2]*dpm2
#println(r)
#println(dot(d(i1),r),"\t",k1 + gamma[i1+1])
return r
end
const abar = make_aj()
function main()
n = 5
kmax = 60
rmax = 30
rfactor = sqrt(2/5)
rmax *= rfactor #rescale
#=
for j=1:n
for i=1:n
println("$i $j ",dot(abar[i],abar[j]))
end
end
=#
pairs = []
for i=0:n-1
for j=i+1:n-1
push!(pairs,(i,j))
end
end
println(pairs)
θs = zeros(Float64,n)
Kset = Set()
#rvalues = Array{Float64,1}[]
Kvalues = Array{Int64,1}[]
vertexvalues = Array{Float64,1}[]
Ks = Vector{Vector{Int64}}(undef,4)
R = zeros(Float64,n)
isum = 0
for pair in pairs
#pair = pairs[1]
i1 = pair[1]
i2 = pair[2]
for k1 = -kmax:kmax
for k2 =-kmax:kmax
isum += 1
#println("$i1 $i2 $k1 $k2")
r = find_intersection(n,i1,i2,k1,k2,gamma)
R = [r[1],r[2],0,0,0] #physical space
#println(dot(abar[i1+1],R),"\t",k1 + gamma[i1+1])
for i=0:n-1
#println(gamma[i+1])
#println("$i ",k1 + gamma[i+1])
θs[i+1] = dot(abar[i+1],R) -gamma[i+1]
if i == i1
θs[i+1] = k1
elseif i == i2
θs[i+1] = k2
end
end
K = round.(θs,RoundDown)
Ks[1] = K[:]
Ks[2] = K[:]
Ks[2][i1+1] += -1
Ks[3] = K[:]
Ks[3][i2+1] += -1
Ks[4] = K[:]
Ks[4][i1+1] += -1
Ks[4][i2+1] += -1
for i=1:4
Ki = Ks[i]
ksub = issubset([Ki],Kset)
if ksub == false
R .= 0
for i=0:n-1
R .+= Ki[i+1]*abar[i+1]
end
R2d = R[1:2] #rescale
if norm(R2d) < rmax
push!(Kset,Ki)
push!(vertexvalues,R2d[:]) #ペンローズタイルの格子点
push!(Kvalues,Ki[:])
end
end
end
end
end
end
num = length(Kvalues)
println(length(Kvalues),"個のPenroseタイルの頂点を見つけました!")
end
main()
これで、vertexvaluesにタイルの点が格納されることになります。図として描きたい場合には、5次元超格子を2次元平面に射影してペンローズタイル準結晶を作ってみよう in Juliaと同じコードを使いまして、結局、プロットするところまで含めた全体のコードは
g1 = 0.1
g2 = 0.7
g3 = -0.98
g4 = 0.43
g5 = -(g1+g2+g3+g4)
const gamma = Float64[g1,g2,g3,g4,g5] #和がゼロだとペンローズタイルになる。
using LinearAlgebra
using Plots
const Θ = 2π/5
d(j) = (sqrt(2/5))*[cos(j*Θ),sin(j*Θ)] #ペンローズタイルを構成する5本のベクトル
function make_aj()
n = 5
abar = Vector{Vector{Float64}}(undef,n)
for j=0:n-1
ϕj = 2π*j/5
abar[j+1] = sqrt(2/5)*[cos(ϕj),sin(ϕj),cos(2ϕj),sin(2ϕj),sqrt(1/2)]
end
return abar
end
function find_intersection(n,i1,i2,k1,k2,gamma)
i1p = ifelse(i1 == n-1,0,i1 + 1)
i1m = ifelse(i1 == 0,n-1,i1 - 1)
i2p = ifelse(i2 == n-1,0,i2 + 1)
i2m = ifelse(i2 == 0,n-1,i2 - 1)
dpm1 = d(i1p) .- d(i1m)
dpm2 = d(i2p) .- d(i2m)
M = [dpm1 -dpm2]
b = (5/2)*((k2 + gamma[i2+1])*d(i2) .- (k1 + gamma[i1+1])*d(i1))
θ = M \ b
r = (5/2)*(k1 + gamma[i1+1])*d(i1) + θ[1]*dpm1
return r
end
const abar = make_aj()
function main()
n = 5
kmax = 60
rmax = 30
rfactor = sqrt(2/5)
rmax *= rfactor #rescale
pairs = []
for i=0:n-1
for j=i+1:n-1
push!(pairs,(i,j))
end
end
println(pairs)
θs = zeros(Float64,n)
Kset = Set()
Kvalues = Array{Int64,1}[]
vertexvalues = Array{Float64,1}[]
Ks = Vector{Vector{Int64}}(undef,4)
R = zeros(Float64,n)
isum = 0
for pair in pairs
#pair = pairs[1]
i1 = pair[1]
i2 = pair[2]
for k1 = -kmax:kmax
for k2 =-kmax:kmax
isum += 1
r = find_intersection(n,i1,i2,k1,k2,gamma)
R = [r[1],r[2],0,0,0] #physical space
for i=0:n-1
#println(gamma[i+1])
#println("$i ",k1 + gamma[i+1])
θs[i+1] = dot(abar[i+1],R) -gamma[i+1]
if i == i1
θs[i+1] = k1
elseif i == i2
θs[i+1] = k2
end
end
K = round.(θs,RoundDown)
Ks[1] = K[:]
Ks[2] = K[:]
Ks[2][i1+1] += -1
Ks[3] = K[:]
Ks[3][i2+1] += -1
Ks[4] = K[:]
Ks[4][i1+1] += -1
Ks[4][i2+1] += -1
for i=1:4
Ki = Ks[i]
ksub = issubset([Ki],Kset)
if ksub == false
R .= 0
for i=0:n-1
R .+= Ki[i+1]*abar[i+1]
end
R2d = R[1:2] #rescale
if norm(R2d) < rmax
push!(Kset,Ki)
push!(vertexvalues,R2d[:]) #ペンローズタイルの格子点
push!(Kvalues,Ki[:])
end
end
end
end
end
end
num = length(Kvalues)
println("isum = $isum")
println(length(Kvalues),"個のPenroseタイルの頂点を見つけました!")
fphop = open("hopindices_"*string(num)*".in","w") #あるペンローズの点における隣り合った点を格納する
fphopnum = open("hopnum_"*string(num)*".in","w") #あるペンローズの点における隣り合った点の数
fpK= open("Kvalues_"*string(num)*".in","w") #5次元座標K
fpxy= open("dotxy_"*string(num)*".in","w") #2次元射影座標(ペンローズタイルになる)
R2dj = zeros(Float64,2)
maxhop = 16
hopindices = zeros(Int64,maxhop,num)
hopnum = zeros(Int64,num)
for i=1:length(Kvalues)
#r = rvalues[i][:] #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
R2d = vertexvalues[i][:] #ペンローズタイルの格子点
Kxy = Kvalues[i][:] #見つけたK
jcount = 0
for j=0:n-1
R2dj .= R2d .+ d(j) #+方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
hopindices[jcount,i] = jhop
end
end
for j=0:n-1
R2dj .= R2d .- d(j) #-方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
hopindices[jcount,i] = jhop
end
end
if jcount == 0
else
for j=0:n-1
print(fpK,Kxy[j+1],"\t")
end
println(fpK,"\t")
println(fpxy,R2d[1],"\t",R2d[2])
println(fphop,"\t")
println(fphopnum,jcount)
hopnum[i] = jcount
end
end
close(fphop)
close(fphopnum)
close(fpK)
close(fpxy)
println("ファイル記録済み。プロット開始。")
c = "red"
lw = 0.5
plot(size=(500,500), legend=false)
for i=1:length(Kvalues)
R2d = vertexvalues[i][:]/rfactor #rescale
for l=1:hopnum[i]
j = hopindices[l,i]
R2dj = vertexvalues[j][:]/rfactor#rescale
plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
rmaxr = 1.1*rmax/rfactor
plot!(xlim=(-rmaxr,rmaxr), ylim=(-rmaxr,rmaxr))
plot!(aspect_ratio=:equal)
savefig("pen_"*string(num)*".pdf")
end
main()
となります。なお、コード上では前回の記事と合わせるためにgammaを使っていますが、これはこの記事では$s_j$のことです。前回の記事でも述べたように、ペンローズタイルにするには、この$s_j$は
\sum_{j=0}^{4} s_j = 0
となるように決めます。コードはJulia 1.8で動作確認をしています。
Ammann–Beenkerタイルのプロットは、このコードを修正して作ってみてください。