突然ですが、準結晶というものを知っていますか?
結晶というのは原子が周期的に規則正しく並んでいます。一方、アモルファスというものもあって、これは原子がぐちゃぐちゃに並んでいます。
準結晶はその中間のようなもので、規則がある感じで並んでいるのにどこにも周期性がない物質です。
この物質は実際に見つかっていて、2011年にノーベル化学賞が得られています(解説)。
この記事では、高次元空間を射影することによって準結晶を作る方法について解説し、Julia言語によるペンローズタイリング作成用のコードを示します。
ペンローズタイル
実際の物質は3次元ですが、2次元の準結晶として有名なものとして、ペンローズタイルがあります。
こんな感じです。
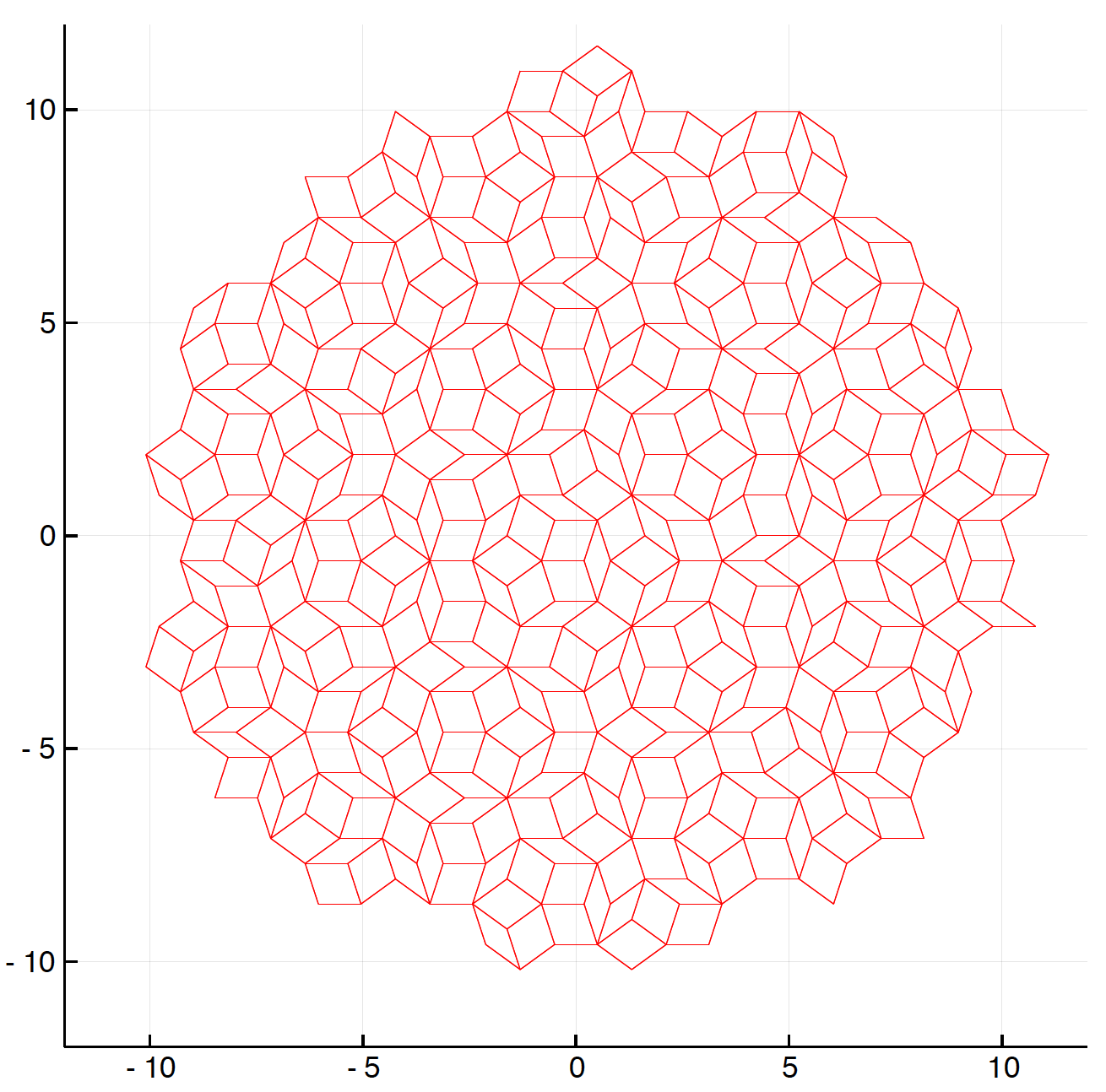
さて、このペンローズタイルを作る方法はいくつかありまして、一番有名なのは、三角形を黄金比で分割して作る方法です。こちらに解説があります(英語)。
他にも方法はあります。
準結晶は規則正しく周期的に並んでいませんが、実はより高次元の結晶の低次元への射影として理解することができます。
例えば、2次元に規則正しく並んでいる正方格子を考えてみましょう。この正方格子を横切るように斜めに直線を引きます。すると、この直線上の点はもちろん1次元です。この直線の近くにある格子点を、この直線上へ射影してみます。
すると、射影された点は周期的には並んでいません。これが準結晶です。動画つき解説(英語)
ペンローズタイリングは、5次元で規則正しく並んでいる超立方格子を2次元平面へ射影することで作られることが知られています(解説(英語))。
5次元空間上の格子
5次元を想像することは難しいですよね。1次元が一つの数字、2次元が二つの数字、3次元が三つの数字を使うことで「場所」を指し示すことができるわけですから、5次元空間は5個の数字を並べれば5次元空間中の場所を指し示すことができるはずです。
この5次元空間上の規則正しく並ぶ格子を考えます。格子を考えるならば、整数を考えれば良いです。例えば、2次元格子であれば、その座標は(i,j)で表すことができます。京都や札幌やマンハッタンの住所みたいなものです。
ですので、5次元空間上の格子の点は
K^T = [K_0,K_1,K_2,K_3,K_4]
と表すことができます。ここでTは転置です。
これは、
R_0^T = [1,0,0,0,0],\\ R_1^T = [0,1,0,0,0], \\
R_2^T = [0,0,1,0,0], \\
R_3^T = [0,0,0,1,0], \\
R_4^T = [0,0,0,0,1]
という5本のベクトルを使って、
R = \sum_{j=0}^{4} K_j R_j
を作れば、5次元空間上の場所を指し示すことができることを意味しています。
低次元の面
次に、低次元への射影について考えます。5次元は大変なので、3次元空間を考えてみましょう。
この3次元空間の中で、平面に射影することを考えます。3次元空間中での任意の平面はどのように特徴付けられるでしょうか?
これは、平行ではない2本の3次元ベクトルd_1,d_2を用意し、その二つのベクトルが作る平行四辺形を考えれば良いです。
この平行四辺形を無限に敷き詰めてやれば、平面が完成します。この平面上の点を指し示すためには、用意した2本のベクトルを使えばよくて、
R_{2d} = x d_1 + y d_2
とすれば良いです。xとyを連続的に動かすことによって、3次元空間のベクトル$R_{2d}$は平面上を動きます。
低次元射影
さて、この平面にはない三次元上の点Rを考えてみます。このベクトルが平面に落とす影を考えてみましょう。
この影は、Rにどのくらいd_1方向成分とd_2方向成分が含まれているかを調べれば良いので、
R_{prod} = (d_1^T R) d_1 + (d_2^T R) d_2
が平面に落とした影を表すベクトルです。三次元空間のベクトルはもともと3本のベクトルからなる:
R = \sum_{j=0}^2 K_j R_j
ことを考えれば、
R_{prod} = \sum_{j=0}^2 K_j (d_1^T R_j) d_1 + \sum_{j=0}^2 K_j (d_2^T R_j) d_2 \\
= x d_1 + y d_2
となります。ここで、x,yは
x = K_0 (d_1^T R_0) + K_1 (d_1^T R_1) + K_2 (d_1^T R_2) \\
y = K_0 (d_2^T R_0) + K_1 (d_2^T R_1) + K_2 (d_2^T R_2)
です。さらに、$r^T = (x,y)$という2次元ベクトルを用意すると、
r = K_0 R_{prod}^0 + K_1 R_{prod}^1 + K_2 R_{prod}^2
と3本の2次元ベクトルを使って書くことができることがわかります。ここで、$[R_{prod}^j]^T =(
(d_1^T R_j),(d_2^T R_j))$です。
このように書くと、もともとの3次元空間における点$[K_0,K_1,K_2]$が射影された時にどのようになっているかがわかりやすくなっています。3本の射影されたベクトルを重みK_jで足せば良い、ということになります。
ペンローズタイリングを特徴づけるベクトル
ペンローズタイリングについて考えます。このタイルは、上の図をよく見ると、5種類の線が繋がってできていることがわかります。5種類の線をベクトルで表すと、
d_j^T =[\cos j \theta, \sin j \theta]
となります。ここで、$\theta = 2\pi/5$です。つまり、半径1の円の上にある正五角形の頂点を表すベクトルです。
ペンローズタイリングで出てくるこの5本のベクトルを「5次元空間から射影されてきた5本のベクトル」とみなしてみましょう。すると、2次元平面上のペンローズタイルの頂点は
r_{prod} = \sum_{j=0}^4 K_j d_j
と書けます。こう書くと、$K_j$は5次元空間を指し示す場所であることがわかります。
ここで、$K_j$には何の制約もかけていないことに注意してください。つまり、$K_j$は座標を示す実数です。
したがって、適当な実数を選んで$r_{prod}$を計算すると、ペンローズタイルには「なりません」。
ここで、ペンローズタイルが5次元空間の格子が射影されてできたものであると仮定します。
すると、$K_j$は整数でなければなりません。
射影
ペンローズタイルを作るのに全ての整数$K_j$を使ってはいけません。なぜなら、全ての整数を使って良いのであれば、無限個あるわけですから、ペンローズタイルのようなパターンは作れません。
つまり、整数$K_j$を制限する必要があります。
ここで、2次元空間上に直線を引いて準結晶を作る方法について思い出してみましょう。
直線を引いた後、その直線に一番近い二次元格子のみを直線に向かって射影することで、1次元準結晶を作ることができます。
つまり、5次元空間上に2次元平面を作って、その2次元平面に一番近い5次元格子点のみを2次元に射影すれば、ペンローズタイルができるはずです。
2次元平面
まず、5次元空間中の2次元平面を作ります。3次元の時と同様に考えると、何らかの5次元ベクトルを2本用意し、そのベクトルがなす平行四辺形を敷き詰める感じで面を作れば良いはずです。つまり、2本のベクトルを$D_1$,$D_2$とすると、
R_{prod} = x D_1 + y D_1
の形になれば良いはずです。
ペンローズタイルにするためには、射影した5本の単位ベクトル$R_j$が$d_j$にならなければなりません。つまり、
これを満たすためには、
d_j^T = [D_1^T R_j,D_2^T R_j]
となる$D_1$,$D_2$を求めれば良いのですが、$D_1^T R_j = [D_1]_j$ですので、
D_1^T = [1,\cos(\theta),\cos(2\theta),\cos(3\theta),\cos(4\theta)] \\
D_2^T = [0,\sin(\theta),\sin(2\theta),\sin(3\theta),\sin(4\theta)]
というベクトルになります。
つまり、
[R_{prod}]_j = x \cos(j \theta) + y \sin (j \theta) = d_j^T r
となります。ここで、$r^T = (x,y)$とおきました。
rを自由に動かすことで、5次元空間中の2次元平面上の点を表現することができます。
さて、2次元平面を作ったのは良いのですが、その位置はどのようにしておけばいいでしょうか。
好きな場所に平面を作りたいので、
[R_{prod}]_j = d_j^T r + \gamma_j
という5次元ベクトル$\gamma^T = [\gamma_0,\gamma_1,\gamma_2,\gamma_3,\gamma_4]$を導入しておきます。これは、2次元空間をカットする直線の位置をずらすのと同じです。
そして、完全に任意に$\gamma$を取ってしまうと、この論文にありますように、一般化ペンローズタイルになってしまいます。普通のペンローズタイルを作る場合には、$\sum_j \gamma_j = 0$となるような$\gamma$を用意すれば良いらしいです。
近接している点の入手
次に、作った平面上に一番近い5次元格子点を探しましょう。
これは、$[R_{prod}]_j$
が実数ですから、この実数を切り上げか切り下げして整数にすれば、一番近い格子点になるはずです。厳密には一番近いのは四捨五入だと思いますが、どれをとっても本質的に変わらないはずですので、切り上げた点を$K_j$とします。つまり、$[R_{prod}]_j = 3.843$なら、$K_j = 4$とします。
つまり、rを指定し、そこから得られた5つの実数を切り上げて5つの整数を作ります。これを$K_j$とします。
この$K_j$を使えば、
r_{prod} = \sum_{j=0}^4 K_j d_j
はペンローズタイルの頂点になります。
ここで一つ注意点です。$\gamma$は$\sum_j \gamma_j =0$を満たすものであれば何でも良いように思えますが、実はそうではありません。特に、$\gamma=0$はダメです。($\gamma=0$がダメだということに気がつくまでに数時間が溶けました。)
詳細な理論については省きますが、
d_j^T r + \gamma_j
が整数となるような$r$の集まりは直線になり、整数の値が異なるたびに異なる直線ができます。また、jが5種類あるので5種類の角度の異なる直線があります。これらをペンタグリッドと呼びます(参考(日本語))。
ペンローズタイルを作るためには、この5種類の直線が常に2本で交点が作られる必要があります。つまり、一つの点に3本以上の直線が交わってはいけない、ようです。交わっていない状況を作る$\gamma$のことをregularと呼ぶようです。$\gamma=0$とするとregularにならず、そのためペンローズタイルが作れません。
Juliaでの実装
これでもうプログラムで実装することができます。
やるべきことは、2次元座標$r$を適当に動かして、その時の5つの整数$K_j$を作ることだけです。
rを少し動かしても同じ整数が出てしまうことから、重複なしで点を集めるようにする必要はあります。
バージョン
Julia 1.4
コード
以下にコードを示します。ここでは、rを円領域にしました。全体のコードは最後に示します。
nr = 1000
ntheta = 500*20
rmax = 5
rs = range(0,rmax,length=nr)
thetas = range(0,2π,length=ntheta+1)
rvalues = Array{Float64,1}[]
Kvalues = Array{Int64,1}[]
vertexvalues = Array{Float64,1}[]
Kset = Set()
fp= open("penrose.in","w")
for ir = 1:nr
for it = 1:ntheta
theta = thetas[it]
x = rs[ir]*cos(theta)
y = rs[ir]*sin(theta)
r = [x,y] #5次元空間中の2次元平面を指し示す座標
Kxy = zeros(Int64,5) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点K
for j=0:4
Kxy[j+1] = K(j,r)
end
if issubset([Kxy],Kset) == false #まだ見つけていないKのセットが見つかった場合
R2d = project(Kxy) #ペンローズタイルの格子点
push!(rvalues,r[:]) #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
push!(vertexvalues,R2d[:]) #ペンローズタイルの格子点
push!(Kvalues,Kxy[:])
push!(Kset,Kxy[:]) #見つけたKを格納する。
println(fp,R2d[1],"\t",R2d[2])
end
end
end
close(fp)
num = length(Kvalues)
println(length(Kvalues),"個のペンローズタイルの頂点を見つけました!")
JuliaにはSetという型がありますので、これを使えば重複なしで点を集めることができます。これで、vertexvaluesの中にペンローズタイルの頂点が格納されました。
このコードでは、dを計算する関数とKを作る関数、そして射影する関数を以下のように定義しました。
Θ = 2π/5
d(j) = [cos(j*Θ),sin(j*Θ)] #ペンローズタイルを構成する5本のベクトル
g1 = 0.1
g2 = 0.7
g3 = -0.98
g4 = 0.43
g5 = -(g1+g2+g3+g4)
const gamma = Float64[g1,g2,g3,g4,g5] #5次元空間中でどの位置に2次元平面を置くかのパラメータ。和がゼロだとペンローズタイルになる。
function K(j,r) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点Kjを探す
round(d(j)'*r+gamma[j+1],RoundUp)
end
function project(K) #探してきた5次元格子点を2次元平面へ射影する
R2d = zeros(Float64,2)
for j=0:4
R2d .+= K[j+1]*d(j)
end
return R2d
end
描画
どうせなら点だけではなく描画もしたいですよね。
一つの点から周りの点に向かって線を引くことにします。どの点が周りの点かどうか判断するためには、周りの点がベクトルdを足して移動できるかどうかを調べれば良いです。そこで、
fphop = open("hopindices_"*string(num)*".in","w") #あるペンローズの点における隣り合った点を格納する
fphopnum = open("hopnum_"*string(num)*".in","w") #あるペンローズの点における隣り合った点の数
fpK= open("Kvalues_"*string(num)*".in","w") #5次元座標K
fpxy= open("dotxy_"*string(num)*".in","w") #2次元射影座標(ペンローズタイルになる)
fpr= open("project_r_"*string(num)*".in","w") #5次元空間中の2次元平面の座標r
R2dj = zeros(Float64,2)
c = "red"
lw = 0.5
plot(size=(500,500), legend=false)
for i=1:length(Kvalues)
r = rvalues[i][:] #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
R2d = vertexvalues[i][:] #ペンローズタイルの格子点
Kxy = Kvalues[i][:] #見つけたK
jcount = 0
for j=0:4
R2dj .= R2d .+ d(j) #+方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
for j=0:4
R2dj .= R2d .- d(j) #-方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
if jcount == 0
else
for j=0:4
print(fpK,Kxy[j+1],"\t")
end
println(fpK,"\t")
println(fpxy,R2d[1],"\t",R2d[2])
println(fpr,r[1],"\t",r[2])
println(fphop,"\t")
println(fphopnum,jcount)
end
end
close(fphop)
close(fphopnum)
close(fpK)
close(fpxy)
close(fpr)
plot!(xlim=(-rmax*3,rmax*3), ylim=(-rmax*3,rmax*3))
plot!(aspect_ratio=:equal)
savefig("pen_"*string(num)*".pdf")
としました。
全体コード
全体のコードは
using LinearAlgebra
using Plots
Θ = 2π/5
d(j) = [cos(j*Θ),sin(j*Θ)] #ペンローズタイルを構成する5本のベクトル
g1 = 0.1
g2 = 0.7
g3 = -0.98
g4 = 0.43
g5 = -(g1+g2+g3+g4)
const gamma = Float64[g1,g2,g3,g4,g5] #5次元空間中でどの位置に2次元平面を置くかのパラメータ。和がゼロだとペンローズタイルになる。
function K(j,r) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点Kjを探す
round(d(j)'*r+gamma[j+1],RoundUp)
end
function project(K) #探してきた5次元格子点を2次元平面へ射影する
R2d = zeros(Float64,2)
for j=0:4
R2d .+= K[j+1]*d(j)
end
return R2d
end
function pen()
nr = 1000
ntheta = 500*20
rmax = 5
rs = range(0,rmax,length=nr)
thetas = range(0,2π,length=ntheta+1)
rvalues = Array{Float64,1}[]
Kvalues = Array{Int64,1}[]
vertexvalues = Array{Float64,1}[]
Kset = Set()
fp= open("penrose.in","w")
for ir = 1:nr
for it = 1:ntheta
theta = thetas[it]
x = rs[ir]*cos(theta)
y = rs[ir]*sin(theta)
r = [x,y] #5次元空間中の2次元平面を指し示す座標
Kxy = zeros(Int64,5) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点K
for j=0:4
Kxy[j+1] = K(j,r)
end
if issubset([Kxy],Kset) == false #まだ見つけていないKのセットが見つかった場合
R2d = project(Kxy) #ペンローズタイルの格子点
push!(rvalues,r[:]) #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
push!(vertexvalues,R2d[:]) #ペンローズタイルの格子点
push!(Kvalues,Kxy[:])
push!(Kset,Kxy[:]) #見つけたKを格納する。
println(fp,R2d[1],"\t",R2d[2])
end
end
end
close(fp)
num = length(Kvalues)
println(length(Kvalues),"個のペンローズタイルの頂点を見つけました!")
fphop = open("hopindices_"*string(num)*".in","w") #あるペンローズの点における隣り合った点を格納する
fphopnum = open("hopnum_"*string(num)*".in","w") #あるペンローズの点における隣り合った点の数
fpK= open("Kvalues_"*string(num)*".in","w") #5次元座標K
fpxy= open("dotxy_"*string(num)*".in","w") #2次元射影座標(ペンローズタイルになる)
fpr= open("project_r_"*string(num)*".in","w") #5次元空間中の2次元平面の座標r
R2dj = zeros(Float64,2)
c = "red"
lw = 0.5
plot(size=(500,500), legend=false)
for i=1:length(Kvalues)
r = rvalues[i][:] #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
R2d = vertexvalues[i][:] #ペンローズタイルの格子点
Kxy = Kvalues[i][:] #見つけたK
jcount = 0
for j=0:4
R2dj .= R2d .+ d(j) #+方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
for j=0:4
R2dj .= R2d .- d(j) #-方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
if jcount == 0
else
for j=0:4
print(fpK,Kxy[j+1],"\t")
end
println(fpK,"\t")
println(fpxy,R2d[1],"\t",R2d[2])
println(fpr,r[1],"\t",r[2])
println(fphop,"\t")
println(fphopnum,jcount)
end
end
close(fphop)
close(fphopnum)
close(fpK)
close(fpxy)
close(fpr)
plot!(xlim=(-rmax*3,rmax*3), ylim=(-rmax*3,rmax*3))
plot!(aspect_ratio=:equal)
savefig("pen_"*string(num)*".pdf")
end
pen()
となります。これによって、最初の図を描いたのでした。
注意点
注意点としては、rの点を離散的に動かしている都合上、nrとnthetaは十分大きく取らなければ格子点を見落とすことになります。ですので、rmaxの値を大きくした場合にはそれに応じてnrとnthetaを大きく撮る必要があります。
ここは無駄なことをしている気もするので、もう少し改善するアルゴリズムはあるかもしれません。
遊び方
冒頭に定義してある$\gamma$を色々といじることで様々なペンローズタイルが出てきます。
追記
rの動かし方について、やはり上のやり方は効率的ではないですね。
ペンタグリッドを使ったrの探索方法についてもここに書いておきます。
5本のペンタグリッドのうち2本を選ぶ方法は
pairs = [(0,1),(0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)]
の10通りです。
そこで、2本を選んできて、その交点周辺のrを持ってくれば、過不足なくペンローズタイルが得られると予想されます。
sとmの二種類を選んだ時、適当な整数K_sとK_mで表現される交点の座標は
d_s^T r + \gamma_s = K_s \\
d_m^T r + \gamma_m = K_m
を満たすrです。これは2x2の逆行列の計算をすれば求めることができます。
つまり、
pairs = [(0,1),(0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)]
dr = 1/10000
rs = Array{Float64,1}[[0,0],[dr,0],[-dr,0],[0,dr],[0,-dr]]
kmax = 20
Θ = 2π/5
for pair in pairs
i1 = pair[1]
i2 = pair[2]
d1 = d(i1)
d2 = d(i2)
M = [
cos(i1*Θ) sin(i1*Θ)
cos(i2*Θ) sin(i2*Θ)
]
Minv = inv(M)
for k1 = -kmax:kmax
for k2 =-kmax:kmax
r = Minv*[k1-gamma[i1+1],k2-gamma[i2+1]]
# r = k1*d1 + k2*d2
for ir = 1:5
r2 = r + rs[ir]
if norm(r2) <= rmax
ksub = findpen!(r2,rvalues,Kvalues,vertexvalues,Kset,fp)
end
end
end
end
end
とすればOKです。ここで、
function findpen!(r,rvalues,Kvalues,vertexvalues,Kset,fp)
Kxy = zeros(Int64,5) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点K
for j=0:4
Kxy[j+1] = K(j,r)
end
ksub = issubset([Kxy],Kset)
if ksub == false #まだ見つけていないKのセットが見つかった場合
R2d = project(Kxy) #ペンローズタイルの格子点
push!(rvalues,r[:]) #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
push!(vertexvalues,R2d[:]) #ペンローズタイルの格子点
push!(Kvalues,Kxy[:])
push!(Kset,Kxy[:]) #見つけたKを格納する。
println(fp,R2d[1],"\t",R2d[2])
end
return ksub
end
を定義しました。
新しいコードの全体は
using LinearAlgebra
using Plots
const Θ = 2π/5
d(j) = [cos(j*Θ),sin(j*Θ)] #ペンローズタイルを構成する5本のベクトル
g1 = 0.1
g2 = 0.7
g3 = -0.98
g4 = 0.43
g5 = -(g1+g2+g3+g4)
const gamma = Float64[g1,g2,g3,g4,g5] #5次元空間中でどの位置に2次元平面を置くかのパラメータ。和がゼロだとペンローズタイルになる。
function K(j,r) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点Kjを探す
round(d(j)'*r+gamma[j+1],RoundUp)
end
function project(K) #探してきた5次元格子点を2次元平面へ射影する
R2d = zeros(Float64,2)
for j=0:4
R2d .+= K[j+1]*d(j)
end
return R2d
end
function findpen!(r,rvalues,Kvalues,vertexvalues,Kset,fp)
Kxy = zeros(Int64,5) #5次元空間中の二次元平面上のr=(x,y)という点に一番近いj次元方向の格子点K
for j=0:4
Kxy[j+1] = K(j,r)
end
ksub = issubset([Kxy],Kset)
if ksub == false #まだ見つけていないKのセットが見つかった場合
R2d = project(Kxy) #ペンローズタイルの格子点
push!(rvalues,r[:]) #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
push!(vertexvalues,R2d[:]) #ペンローズタイルの格子点
push!(Kvalues,Kxy[:])
push!(Kset,Kxy[:]) #見つけたKを格納する。
println(fp,R2d[1],"\t",R2d[2])
end
return ksub
end
function pen()
nr = 1000
ntheta = 1000
rmax = 10
rs = range(0,rmax,length=nr)
thetas = range(0,2π,length=ntheta+1)
rvalues = Array{Float64,1}[]
Kvalues = Array{Int64,1}[]
vertexvalues = Array{Float64,1}[]
Kset = Set()
fp= open("penrose.in","w")
pairs = [(0,1),(0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)]
dr = 1/10000
rs = Array{Float64,1}[[0,0],[dr,0],[-dr,0],[0,dr],[0,-dr]]
kmax = 20
Θ = 2π/5
for pair in pairs
i1 = pair[1]
i2 = pair[2]
d1 = d(i1)
d2 = d(i2)
M = [
cos(i1*Θ) sin(i1*Θ)
cos(i2*Θ) sin(i2*Θ)
]
Minv = inv(M)
for k1 = -kmax:kmax
for k2 =-kmax:kmax
r = Minv*[k1-gamma[i1+1],k2-gamma[i2+1]]
# r = k1*d1 + k2*d2
for ir = 1:5
r2 = r + rs[ir]
if norm(r2) <= rmax
ksub = findpen!(r2,rvalues,Kvalues,vertexvalues,Kset,fp)
end
end
end
end
end
close(fp)
num = length(Kvalues)
println(length(Kvalues),"個のペンローズタイルの頂点を見つけました!")
fphop = open("hopindices_"*string(num)*".in","w") #あるペンローズの点における隣り合った点を格納する
fphopnum = open("hopnum_"*string(num)*".in","w") #あるペンローズの点における隣り合った点の数
fpK= open("Kvalues_"*string(num)*".in","w") #5次元座標K
fpxy= open("dotxy_"*string(num)*".in","w") #2次元射影座標(ペンローズタイルになる)
fpr= open("project_r_"*string(num)*".in","w") #5次元空間中の2次元平面の座標r
R2dj = zeros(Float64,2)
maxhop = 7
hopindices = zeros(Int64,maxhop,num)
hopnum = zeros(Int64,num)
for i=1:length(Kvalues)
r = rvalues[i][:] #2次元平面上でのr=(x,y)。格子点はこれに一番近い整数のKから作られる。
R2d = vertexvalues[i][:] #ペンローズタイルの格子点
Kxy = Kvalues[i][:] #見つけたK
jcount = 0
for j=0:4
R2dj .= R2d .+ d(j) #+方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
hopindices[jcount,i] = jhop
end
end
for j=0:4
R2dj .= R2d .- d(j) #-方向を探す
jhop = findfirst(x -> norm(x-R2dj) < 1e-12,vertexvalues) #あるペンローズ格子点の隣り合った点を探す。
if jhop != nothing
jcount += 1
print(fphop,jhop,"\t")
hopindices[jcount,i] = jhop
#plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
if jcount == 0
else
for j=0:4
print(fpK,Kxy[j+1],"\t")
end
println(fpK,"\t")
println(fpxy,R2d[1],"\t",R2d[2])
println(fpr,r[1],"\t",r[2])
println(fphop,"\t")
println(fphopnum,jcount)
hopnum[i] = jcount
end
end
close(fphop)
close(fphopnum)
close(fpK)
close(fpxy)
close(fpr)
println("ファイル記録済み。プロット開始。")
c = "red"
lw = 0.5
plot(size=(500,500), legend=false)
for i=1:length(Kvalues)
R2d = vertexvalues[i][:]
for l=1:hopnum[i]
j = hopindices[l,i]
R2dj = vertexvalues[j][:]
plot!([R2d[1],R2dj[1]], [R2d[2], R2dj[2]], color=c, lw=lw)
end
end
plot!(xlim=(-rmax*3,rmax*3), ylim=(-rmax*3,rmax*3))
plot!(aspect_ratio=:equal)
savefig("pen_"*string(num)*".pdf")
end
pen()
となります。