フィボナッチ数列は再帰関数の題材として適切なのか

はじめに

プログラミングを始めたての頃、フィボナッチ数列を題材に再帰関数を書いてみるという経験をした方は多いのではと思います。
再帰関数は漸化式のような数式で表せる場合などに用いられることがあります。そしてフィボナッチ数列は漸化式で表すことができ、知名度も高いので再帰関数のサンプルとなっています。
ただこのフィボナッチ数列には一癖も二癖もあり、再帰関数の題材としてどうなの？って思ったのでそのことについてpythonで解説していきます。

実装

まずは何も考えず

フィボナッチ数列は以下の漸化式で与えられます。

\begin{align}
F_0 &= 0 \\
F_1 &= 1 \\
F_{n+2} &= F_n + F_{n+1}  \quad (n ≥ 0) \\
\end{align}

ではこれを再帰関数を用いて書いていきます。

def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

解説すると再帰関数のベースケースとしてn==0, n==1を与え、それ以外は直前の2項の和を返り値としています。
実際に実行してみるとうまく計算できてそうです。

fibonacci(5)
5
fibonacci(10)
55

さてこれで全く問題なそうに見えますが...

問題点① 処理遅い問題

先ほど書いた関数の引数に100を与えてみます。

fibonacci(100)

...
...
...

CPUが100%に張り付いて処理が終わらなくなってしまいました。

なぜこうなってしまったかについて解説します。
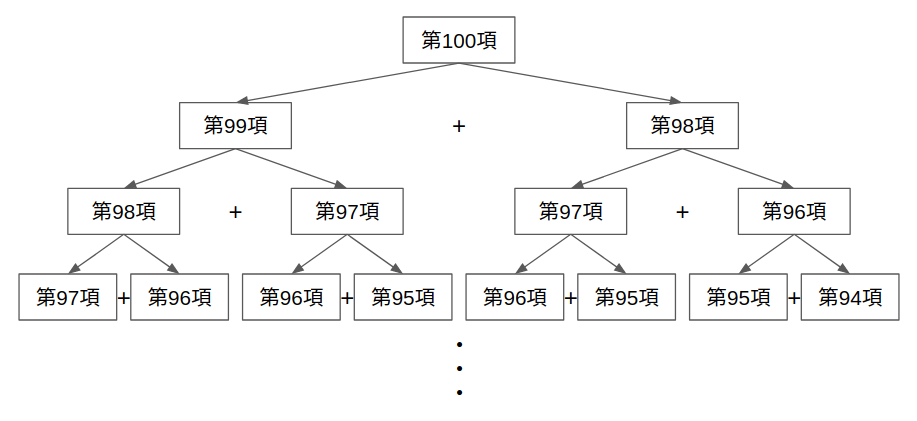
実際には以下の図のように第100項を求めるのに第99項と第98項の結果を求めて、またその第99項を求めるのに第98項と第97項の結果を求めて...という処理を繰り返します。

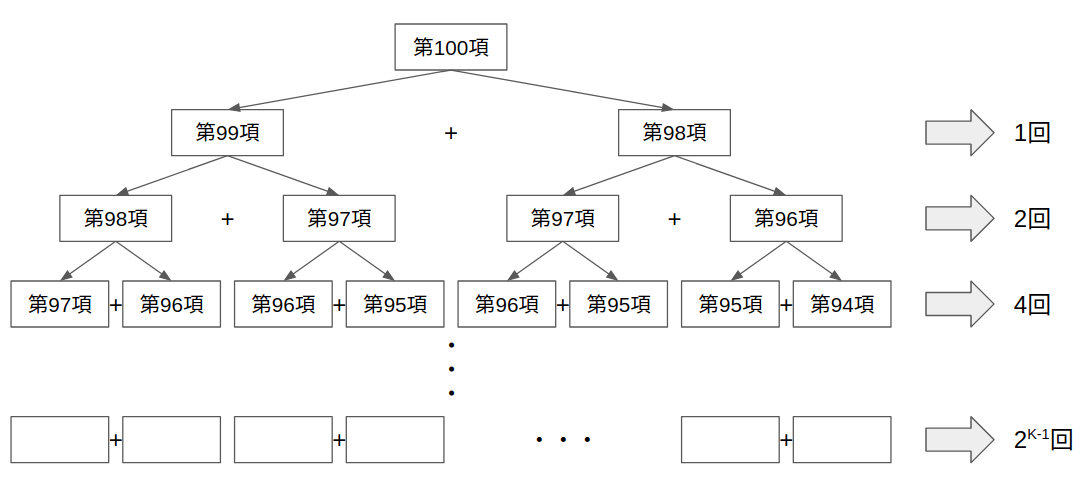
必要な足し算の回数は下に行くに連れて倍々で増えていくのでk段目で行われる足し算の回数は$2^{k-1}$回になります。(正確にはベースケースに到達する速度が左右の枝で異なるので微妙に違う)
計算量(オーダー)は$O(2^n)$となります。

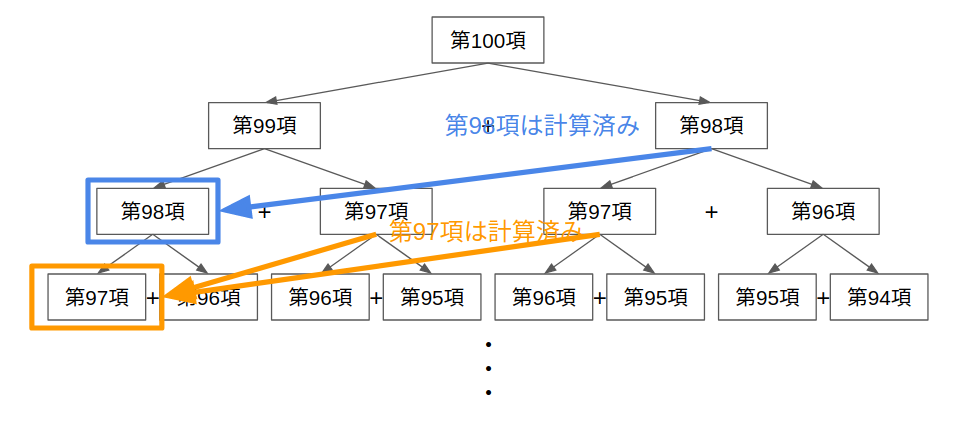
この計算量を減らすべく、上記の図で重複している項に注目します。例えば第98項は、第100項を求めるときと第99項を求めるときで2回登場しています。どちらかの計算結果を用いることで計算量を減らせそうです。常に左枝の項から計算するとすると第$k-2$項は第$k-1$項を求めるときにすでに計算済みということが言えます。図で説明すると右枝の項は左枝の項を求めるときにどこかですでに計算済みということです。

$k<=1$のとき(ベースケース)と第$k-2$項を求めるときはキャッシュを参照するように書き換えています。

cache = {0: 0, 1: 1}  # ベースケースのキャッシュを作成
def fibonacci(n):
    if n <= 1:
        return cache[n]
    else:
        cache[n - 1] = fibonacci(n - 1)
        return cache[n - 1] + cache[n - 2]

実行してみるとすぐさま結果を返してくれます。

fibonacci(100)
354224848179261915075
fibonacci(500)
139423224561697880139724382870407283950070256587697307264108962948325571622863290691557658876222521294125

最初に書いたプログラムでは関数内で最大2回、自分自身を呼び出すため計算量が$O(2^n)$となっていましたが、今回は最大でも1度しか呼び出すことがありません。計算量は$O(n)$となります。また図の左端の項のみを求めていくだけでという点からもそれがわかるかと思います。

さてこれで一見落着と思いきや...

問題点② スタックオーバーフロー

さて先程のプログラムを用いて第1000項を求めます。

fibonacci(1000)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 5, in fibonacci
  File "<stdin>", line 5, in fibonacci
  File "<stdin>", line 5, in fibonacci
  [Previous line repeated 995 more times]
  File "<stdin>", line 2, in fibonacci
RecursionError: maximum recursion depth exceeded in comparison

エラーとなりました。これはスタックオーバーフローです。関数内で自身を呼び出すことで際限なくスタックが積み重なっていることが原因です。回避策としては以下の2つがあるかと思います。

• 上限を増やす
• 再帰末尾による最適化

それぞれ見ていきます。

上限を増やす

これはとてもシンプルです。標準ライブラリのsysのsetrecursionlimitに上限とするスタック数を入力します。

import sys
sys.setrecursionlimit(1500)

ではもう一度第1000項を求めてみます。

fibonacci(1000)
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875

エラーとならず実行できました。
ただこれは上限が決まっている場合に限られるので第2000項を求めようとすると当然エラーになります。使用するメモリなども考慮するとむやみにここを増やすことは得策とは言えません。何よりエレガントではないです。

再帰末尾による最適化

再帰末尾による最適化はこの記事を書くための調査をするまで全く知らなかったのですが、計算途中の値がそれ以上使用されない場合にスタックを新規で作成せず、再利用してくれるようです。
この記事を参考にさせていただきました。https://qiita.com/pebblip/items/cf8d3230969b2f6b3132

ただpythonはこの再帰末尾による最適化に対応してないので自分で作成する必要があります。
pythonの再帰末尾による最適化はこの記事を参考にしました。http://tanihito.hatenablog.com/entry/20110119/1295459297
以下のプログラムは上記リンクの抜粋になります。解説は省略しますが、このtail_recursiveというデコレータをつけるとその関数は再帰末尾による最適化に対応できます。

from functools import wraps

def tail_recursive(func):
   self_func = [func]
   self_firstcall = [True]
   self_CONTINUE = [object()]
   self_argskwd = [None]

   @wraps(func)
   def _tail_recursive(*args, **kwd):
       if self_firstcall[0] == True:
           func = self_func[0]
           CONTINUE = self_CONTINUE
           self_firstcall[0] = False
           try:
               while True:
                  result = func(*args, **kwd)
                   if result is CONTINUE:  # update arguments
                      args, kwd = self_argskwd[0]
                   else:  # last call
                       return result
           finally:
               self_firstcall[0] = True
       else:  # return the arguments of the tail call
           self_argskwd[0] = args, kwd
           return self_CONTINUE

   return _tail_recursive

そもそも今回取り上げているフィボナッチ数列は再帰末尾による最適化を利用するための計算途中の値を利用しないということが難しいです。これは「第$n$項を求めるには、第$n-1$項と第$n-2$項が必要で、第$n-1$項を求めるには第$n-2$項と第$n-3$項が...」という考え方を元にプログラムを書いており、たとえば、第100項を求める際の第99項と第98項が計算途中の値として必要になるためです。

ということで元にしている考え方を変える必要があります。
「第$k$項と第$k+1$項の計算結果用いて第$k+2$項を求めるという処理を、$k=0$から$k=n$(第n項が求まる)まで繰り返す」という考え方であれば計算結果を引数に再帰関数を実行できるので良さそうです。それでは、プログラムを書いてみます。

def fibonacci(n):

    @tail_recursive
    def fibonacci_recursive(k, fk, fk_1):
        if k == n:
            return fk
        else:
            return fibonacci_recursive(k + 1, fk_1, fk + fk_1)

    return fibonacci_recursive(0, 0, 1)

プログラムを解説します。
現在計算しているのが第何項なのかという値を変数k、第$k$項と第$k+1$項の値をそれぞれ変数fk、fk_1とおいています。
kがnに到達したら、計算終了です。@tail_recursiveは再帰末尾による最適化に対応するためのデコレータです。

それでは実行してみます。

fibonacci(10000)
33644764876431783266621612005107543310302148460680063906564769974680081442166662368155595513633734025582065332680836159373734790483865268263040892463056431887354544369559827491606602099884183933864652731300088830269235673613135117579297437854413752130520504347701602264758318906527890855154366159582987279682987510631200575428783453215515103870818298969791613127856265033195487140214287532698187962046936097879900350962302291026368131493195275630227837628441540360584402572114334961180023091208287046088923962328835461505776583271252546093591128203925285393434620904245248929403901706233888991085841065183173360437470737908552631764325733993712871937587746897479926305837065742830161637408969178426378624212835258112820516370298089332099905707920064367426202389783111470054074998459250360633560933883831923386783056136435351892133279732908133732642652633989763922723407882928177953580570993691049175470808931841056146322338217465637321248226383092103297701648054726243842374862411453093812206564914032751086643394517512161526545361333111314042436854805106765843493523836959653428071768775328348234345557366719731392746273629108210679280784718035329131176778924659089938635459327894523777674406192240337638674004021330343297496902028328145933418826817683893072003634795623117103101291953169794607632737589253530772552375943788434504067715555779056450443016640119462580972216729758615026968443146952034614932291105970676243268515992834709891284706740862008587135016260312071903172086094081298321581077282076353186624611278245537208532365305775956430072517744315051539600905168603220349163222640885248852433158051534849622434848299380905070483482449327453732624567755879089187190803662058009594743150052402532709746995318770724376825907419939632265984147498193609285223945039707165443156421328157688908058783183404917434556270520223564846495196112460268313970975069382648706613264507665074611512677522748621598642530711298441182622661057163515069260029861704945425047491378115154139941550671256271197133252763631939606902895650288268608362241082050562430701794976171121233066073310059947366875

第10000項でも一瞬で計算できます。
これでスタックオーバーフロー問題も克服できたかに思えますが...

普通にfor文で書いてみる

先程の再帰末尾による最適化に対応する際に「第$k$項と第$k+1$項の計算結果用いて第$k+2$項を求めるという処理を、$k=0$から$k=n$(第n項が求まる)まで繰り返す」という考え方でプログラムを書きました。
勘のいい方だとお気づきかと思いますが、これってただのfor文の考え方と一緒なんですよね。
ということで以下にフィボナッチ数列をfor文で書いてみました。

def fibonacci(n):
    fk, fk_1 = 0, 1
    for k in range(n):
        fk, fk_1 = fk_1, fk + fk_1
    return fk

変数の意味は、先程と同様で現在計算しているのが第何項なのかという値を変数k、第$k$項と第$k+1$項の値をそれぞれ変数fk、fk_1とおいています。(kは使っていませんが。)
実行してみます。

fibonacci(10000)
33644764876431783266621612005107543310302148460680063906564769974680081442166662368155595513633734025582065332680836159373734790483865268263040892463056431887354544369559827491606602099884183933864652731300088830269235673613135117579297437854413752130520504347701602264758318906527890855154366159582987279682987510631200575428783453215515103870818298969791613127856265033195487140214287532698187962046936097879900350962302291026368131493195275630227837628441540360584402572114334961180023091208287046088923962328835461505776583271252546093591128203925285393434620904245248929403901706233888991085841065183173360437470737908552631764325733993712871937587746897479926305837065742830161637408969178426378624212835258112820516370298089332099905707920064367426202389783111470054074998459250360633560933883831923386783056136435351892133279732908133732642652633989763922723407882928177953580570993691049175470808931841056146322338217465637321248226383092103297701648054726243842374862411453093812206564914032751086643394517512161526545361333111314042436854805106765843493523836959653428071768775328348234345557366719731392746273629108210679280784718035329131176778924659089938635459327894523777674406192240337638674004021330343297496902028328145933418826817683893072003634795623117103101291953169794607632737589253530772552375943788434504067715555779056450443016640119462580972216729758615026968443146952034614932291105970676243268515992834709891284706740862008587135016260312071903172086094081298321581077282076353186624611278245537208532365305775956430072517744315051539600905168603220349163222640885248852433158051534849622434848299380905070483482449327453732624567755879089187190803662058009594743150052402532709746995318770724376825907419939632265984147498193609285223945039707165443156421328157688908058783183404917434556270520223564846495196112460268313970975069382648706613264507665074611512677522748621598642530711298441182622661057163515069260029861704945425047491378115154139941550671256271197133252763631939606902895650288268608362241082050562430701794976171121233066073310059947366875

再帰末尾による最適化に対応したプログラムと全く同じ結果です。

なんと短くて読みやすいことでしょう。
処理が遅かったりスタックオーバーフローが発生するということもありません。
もしかしてこっちのほうがいいのでは...

まとめ

再帰関数は、プログラミングに対する理解を深めることができ、またその記述はとてもエレガントです。
ただ"再帰関数が使える＝再帰関数を使うべき"としてしまうのは間違いだと言えそうです。すくなくともフィボナッチ数列では、for文で書いた初項から計算するプログラムのほうが恒久的です。また最初に漸化式であれば再帰関数を用いる場合があるとしましたが、一般項を求めることができるならそれを元にプログラムすることで今回提起した問題が発生することが少なくなりそうです。(可読性という問題が発生する可能性はありますが)
再帰関数の学習のみというスコープではフィボナッチ数列はいい題材かもしれませんが、実運用まで考えると(フィボナッチ数列を実運用？)あまり適切ではない気がしました。

以上フィボナッチ数列は再帰関数の題材として適切なのかでした。

参考文献

以下の記事を参考にさせていただきました。
https://qiita.com/pebblip/items/cf8d3230969b2f6b3132
https://qiita.com/ryo2132/items/4bedeec846d0427f1ac7
http://tanihito.hatenablog.com/entry/20110119/1295459297