問題
2×2 のマス目の左上からスタートした場合, 引き返しなしで右下にいくルートは 6 つある.
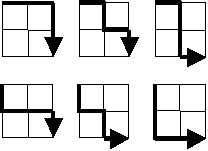
では, 20×20 のマス目ではいくつのルートがあるか.
http://odz.sakura.ne.jp/projecteuler/index.php?cmd=read&page=Problem%2015
回答方針1
組み合わせの数でも求められるけど、せっかくなので別なアルゴリズムを試したい。
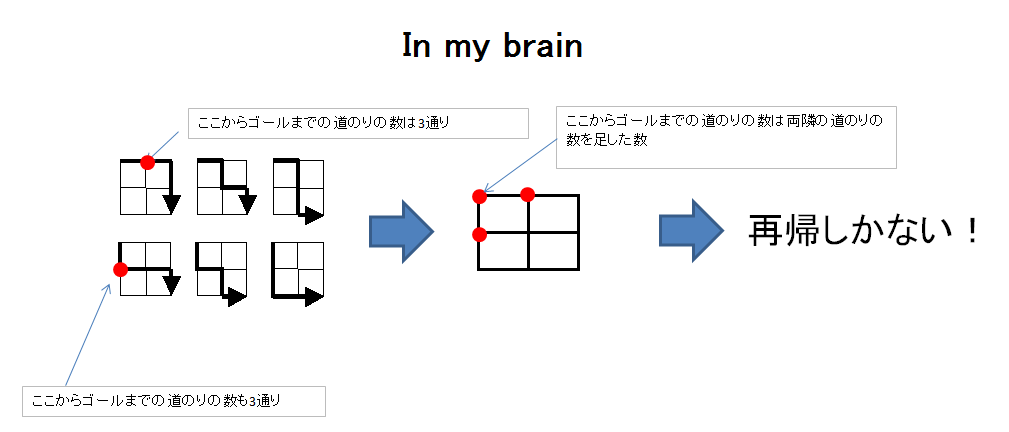
あるマスからゴールまでの道のりの数は、当該マスに隣接する進行方向の2マスそれぞれからのゴールまでの道のりの数の和に等しい。
→再起しかない!
コード1
def f(L,a,b):
if not L[a][b]:
if a == len(L)-1 or b == len(L)-1:
L[a][b] = 1
else:
L[a][b] = f(L,a+1,b) + f(L,a,b+1)
return L[a][b]
def main():
#(x,y) = (2,2)
(x,y) = (20,20)
L = [[0 for i in range(0,y+1)] for j in range(i,x+1)]
ans = f(L,0,0)
#print ans
回答方針2
ウェブを調べると、ゴールまでの道のりの数ではなく、起点からの道のりの数をfor文でどんどん求めいくやり方が見受けられた。実際に試してみたがfor文のほうが遥かに速かった。
少し考察したところ、アルゴリズムとして当該やり方の方が効率良さそうである。
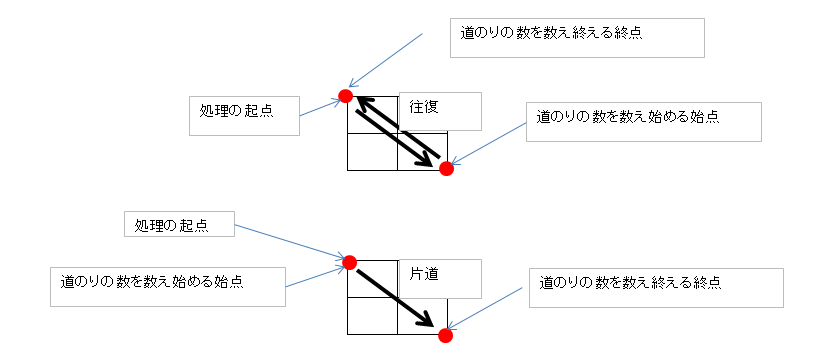
せっかくなので、対称性も勘案して半分だけ求めるようにしてみた。

コード2
def g(L,a,b):
if a == 0:
return 1
elif a == b:
return L[a-1][b]*2
else:
return L[a-1][b]+L[a][b-1]
def main2():
seq = range(21)
L = [[0 for i in seq] for j in seq]
for a in seq:
for b in seq[a:]:
L[a][b] = g(L,a,b)
#print L[20][20]