データの統計解析と可視化の演習3（Kaggleのタイタニック）

概要

-「その2」のつづきとなります。Kaggleのタイタニック号のデータを使って、統計解析とデータの可視化をしていきます。
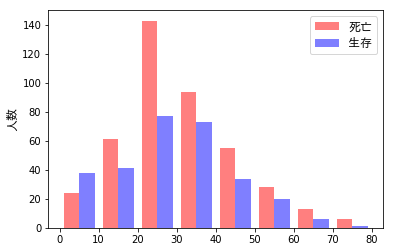
- 前回の「その2」では、次のようなヒストグラムを作成しました。今回は、各階級（年齢範囲）の死亡率／生存率についてグラフを作成していきます。また、各階級（年齢範囲）と性別による死亡率についても求めていきます。

準備

データを読み込みます。詳細については「その1」を参照してください。

from IPython.display import display
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
df = pd.read_csv('train.csv')

ビン分割（各年齢階級の度数を求める）

df.plot.hist() では、内部で各年齢階級の度数を計算してヒストグラムを描いてくれました。今回は、データフレーム上で各階級の度数、つまり、0歳より大きく10歳以下（これを (0, 10] のように表記）の人数、10歳より大きく20歳以下（これを (0, 10]）の人数・・・を計算していきます。

この処理（ビン分割）は、次のように pd.cut() を利用して行なうことができます。

bins = list(range(0,81,10))
s = pd.cut(df['Age'], bins).value_counts().sort_index()
display(s)

実行結果

(0, 10]      64
(10, 20]    115
(20, 30]    230
(30, 40]    155
(40, 50]     86
(50, 60]     42
(60, 70]     17
(70, 80]      5
Name: Age, dtype: int64

この実行結果からは「年齢が0歳より大きく10歳以下の人は 64名 いた」といったことが分かります。

コード中の list(range(0,81,10)) では、[0, 10, 20, 30, 40, 50, 60, 70, 80] というリストを生成します。これを cut の第2引数として与えることで任意の階級でのビン分割をしてくれます。境界の扱いは「 $0<x\le10$、 $10<x\le20$、・・・、$70<x\le80$ 」のようになります（オプションで right=False を指定すると「$0\le x<10$、 $10\le x<20$、・・・、$70\le x<80$」となります）。

各年齢階級の死亡／生存の度数を求める

各階級の生存者数と死亡者数を求めていきます。

df0= df[df['Survived']==0]
df1= df[df['Survived']==1]
bins = list(range(0,81,10))
s0 = pd.cut(df0['Age'], bins).value_counts().sort_index()
s1 = pd.cut(df1['Age'], bins).value_counts().sort_index()
dfx = pd.DataFrame({'死亡':s0, '生存':s1})
dfx = dfx.assign( **{'全体': lambda p: p.sum(axis=1)} )
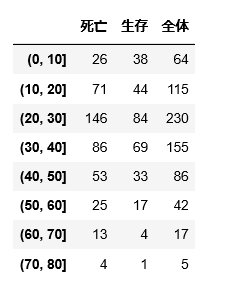
display(dfx)

上記のように各階級ごとの生存者数、死亡者数を求めることができました。

各年齢階級の死亡率／生存率を求める

生存／死亡の人数を割合（確率）に変換します。

t = dfx.apply( lambda p: p/p[-1] , axis=1 )
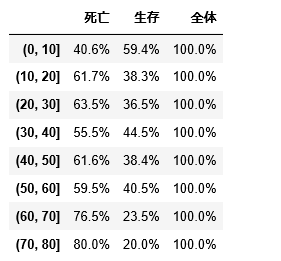
display(t.applymap( lambda p: '{0:>5.1%}'.format(p))) # 百分率に変換

このように割合に変換することで「60代、70代の死亡率が高い」といったことがはっきりと分かりますね。

各年齢階級の死亡率／生存率をグラフで表現

各階級の死亡率／生存率をグラフにしていきます。積み上げ式の横方向の棒グラフを使用します。最初の2行はグラフで日本語を表示するためのものです（詳しくは「その2」を参照してください）。

積み上げ式の横棒グラフは barh(stacked=True) で描画できます。

from matplotlib.font_manager import FontProperties
fp= FontProperties(fname='ipaexg.ttf', size=12);

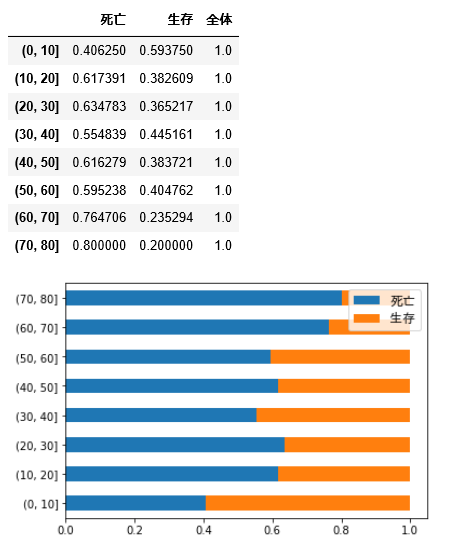
t = dfx.apply( lambda p: p/p[-1] , axis=1 )
display(t)
col = ['死亡','生存'] 
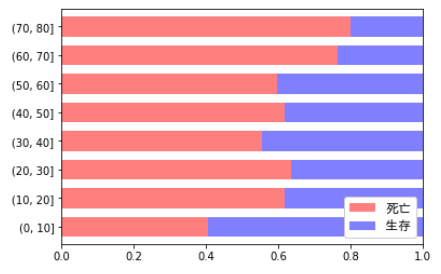
t[col].plot.barh(stacked=True)
plt.legend(col, prop=fp)
plt.show()

デフォルト状態では、いまいち美しくないので整形します。凡例の位置設定、透明度設定などを行なってきます。

col = ['死亡','生存'] 
t[col].plot.barh(stacked=True, color=['r','b'], alpha=0.5, width=0.7)
plt.xlim(0,1)
plt.legend(col, prop=fp, loc='lower right').get_frame().set_alpha(1.0)
plt.show()

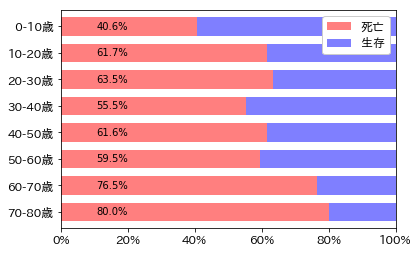
さらに整形していきます（X軸をパーセント表示にして、Y軸の表記を「XX-XX歳」に変えて低年齢のほうがグラフ上部にくるようにして、バー上に死亡率を表示するようにします）。

最終

%matplotlib inline

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from IPython.display import display

fp= FontProperties(fname='ipaexg.ttf', size=12);

df = pd.read_csv('train.csv')
df0= df[df['Survived']==0]
df1= df[df['Survived']==1]

bins = list(range(0,81,10))
s0 = pd.cut(df0['Age'], bins).value_counts().sort_index()
s1 = pd.cut(df1['Age'], bins).value_counts().sort_index()
dfx = pd.DataFrame({'死亡':s0, '生存':s1})
dfx = dfx.assign( **{'全体': lambda p: p.sum(axis=1)} )

t = dfx.apply( lambda p: p/p[-1] , axis=1 )
t = t.iloc[::-1]
col = ['死亡','生存'] 
ax = t[col].plot.barh(stacked=True, color=['r','b'], alpha=0.5, width=0.7)

ax.set_xlim(0,1)
plt.legend(col, prop=fp).get_frame().set_alpha(1.0)

# X軸のラベルを % に変換
vals = ax.get_xticks()
ax.set_xticklabels(['{0:.0%}'.format(x) for x in vals], fontproperties=fp)

# Y軸のラベルを XX-XX歳 に設定
ylabels = [ '{0:>2}-{1:>2}歳'.format(p,p+10) for p in range(0,71,10)]
ylabels.reverse()
ax.set_yticklabels(ylabels, fontproperties=fp)

# バー上に 死亡率を表示
tmp = t['死亡'].tolist();
for i in range(len(tmp)):
    plt.text(0.2, i, '{:>4.1%}'.format(tmp[i]), ha='right', va='center')

plt.show()

性別ごとに各年齢階級の死亡率を求める

性別と年齢を与えたときの死亡割合を計算してみます。この情報は予測「入力（年齢・性別）$\to$ 出力（死亡確率）」にも利用することができます。

import pandas as pd
from IPython.display import display

df = pd.read_csv('train.csv')

df_male   = df[df['Sex']=='male']    # 男性
df_female = df[df['Sex']=='female']  # 女性
df0male   = df_male  [df_male  ['Survived']==0]  # 男性・死亡
df0female = df_female[df_female['Survived']==0]  # 女性・死亡

bins = list(range(0,81,10))
#> [0, 10, 20, 30, 40, 50, 60, 70, 80]
g = ['{0:>2}-{1:>2}歳'.format(bins[i],bins[i+1]) for i in range(len(bins)-1)]
#> [' 0-10歳', '10-20歳',・・・,'60-70歳', '70-80歳']

pFormat = lambda x: '{:>5.1%}'.format(x) if not pd.isnull(x) else 'N/A'

s_male   = pd.cut(df_male  ['Age'], bins, labels=g).value_counts().sort_index()
s0male   = pd.cut(df0male  ['Age'], bins, labels=g).value_counts().sort_index()
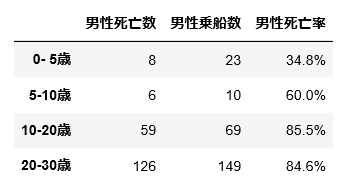
dfxa = pd.DataFrame({'男性死亡数':s0male, '男性乗船数':s_male})
dfxa['男性死亡率'] = ( dfxa['男性死亡数'] / dfxa['男性乗船数'] ).apply(pFormat)
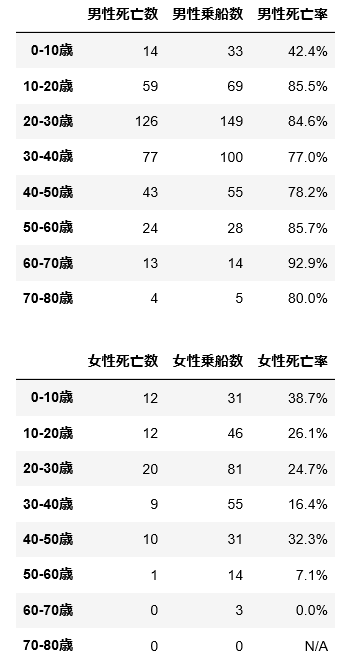
display(dfxa) # 男性 年齢別の死亡数、乗船数、死亡率

s_female = pd.cut(df_female['Age'], bins, labels=g).value_counts().sort_index()
s0female = pd.cut(df0female['Age'], bins, labels=g).value_counts().sort_index()
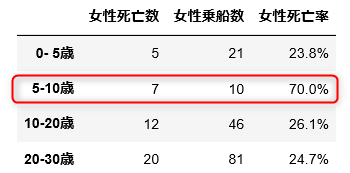
dfxb = pd.DataFrame({'女性死亡数':s0female, '女性乗船数':s_female})
dfxb['女性死亡率'] = ( dfxb['女性死亡数'] / dfxb['女性乗船数'] ).apply(pFormat)
display(dfxb) # 女性 年齢別の死亡数、乗船数、死亡率

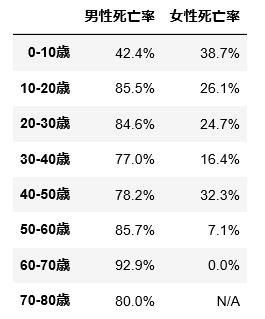
dfx = pd.DataFrame({'男性死亡率':dfxa['男性死亡率'], '女性死亡率':dfxb['女性死亡率']})
display(dfx)

この結果から、最も高い確率（92.9%）で死亡フラグが立つのは「男性・60-70歳」ということが分かります。逆に最も確率が低いのは「女性・60-70歳」ですが、3名分のサンプルから計算した値なので信頼性は低いです。なお「女性・70-80歳」については乗船情報が存在しないため N/A（Not Available：利用不可）としています。

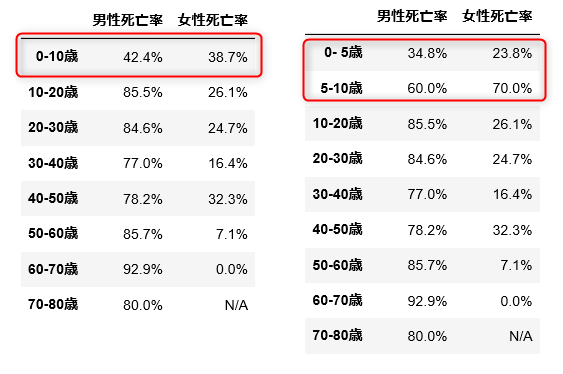
ところで「その1」のなかで低年齢者の死亡率が「極めて低い」ということに気付きました。ただ、ここでの結果では「0-10歳」の死亡率が「極めて」低いということはありません。次のように 0-10歳 の階級を2つに分割して再度計算してみます。

#bins = list(range(0,81,10))
bins = [0, 5, 10, 20, 30, 40, 50, 60, 70, 80]

こうすることで、次に示すように「女性／男性・0-5歳」は死亡率がかなり低いこと、「女性・5-10歳」では死亡率が70%と非常に高いことが新たに浮かんできました。

統計解析する場合には、このように階級の切り方にも十分に注意する必要があります。