「ひともすなるRustといふものをしてみむと」思いたちました。「The Rust Programming language」を読んでみると、とても良くできているように見えます。C/C++プログラムをRustに移植したら安定性が増すのでは?
ただ、C/C++に比べてパフォーマンスはどうでしょうか。複雑なロジックの記述が可能でしょうか?
Rustに詳しい人にとってはそんなことは自明なのでしょうが、長年C/C++を触ってきたけれどもRustのことは何も知らない私にとっては、やはり自分の体で感じないと分かった気になれません。
そこで思いついたのが、6x6盤オセロの完全解1を求めるC++プログラムをRustに移植することです。
元のプログラムは、Deep Learning をオセロで検証する過程で制作したものです。ビット演算やCPUの組込み関数を操作するようなマシン語レベルに近い記述が含まれているため、Rustの性能を測る良い基準になりそうです。またクラスをジェネリック引数にしたテンプレートでクラスを記述するという、やや複雑なロジックも用いていますので、Rustの記述性能を実感できると期待しました。
ここでは、C++からRustへの移植に際して、当初に設定した課題とRustに対する(C++と比較した)評価を紹介します。Rustに詳しい方からすれば課題設定が的外れに見えるかも知れませんが、Rustの素人のこととお許しください。あくまでもC++ユーザ側からの評価です。なお、使用したコンパイラとOSは、以下です。
- C++: g++ (v8.3.0)
- Rust: v1.48.0
- OS: debian 10.7
長くなりますので最初に検証結果を示します。詳しい内容は後で説明します。
なお、関連するコードはGitHubにアップロードしました
検証結果
| 課題 | 内容 | Rustへの評価 |
|---|---|---|
| 課題1 | テンプレートクラスの記述(static関数のみ) | ◎ |
| 課題2 | テンプレートクラスの記述 | ◯ |
| 課題3 | ビルトイン関数 | ◯ |
| 課題4 | 実行性能 | ◯ (C++の96%) |
| 追加比較 | バイナリサイズ | ◯ |
| 総合評価 | 今後の充実への期待もこめて | ◎ |
私が最も重視していた実行性能は、C++の96%(実行時間が1.04倍)でした。全く遜色ない性能です。科学技術計算にRustを利用することも考慮できる水準です。Rustの安定性を考慮すると、Rustが利用される分野が大きくなっていくでしょう。
この記事を書いた時点では、実行性能がC++に比べて74%と記述していましたが、Rustの検証用プログラムにinlineアトリビュートを加えたところ、パーフォーマンスが大幅に向上しました。これについてはインライン展開の項で説明します。
検証課題の説明と評価
課題1. クラスを引数にしたテンプレートでクラスを記述する(static関数のみのクラス)
最初に、ここで言うC++のクラスとは、classとstructの両方を含むことを断っておきます(アクセス権以外の違いはありませんから)。
何故、表題のようなロジックが必要なのか。それは、図1のようにオセロ盤にも様々な種類があるからです2。ところが、アルゴリズムの多くの部分はオセロ盤のサイズにかかわらず共通です。盤のサイズによる違いは、いくつかの定数とビット操作を行うたった4個の関数に凝縮されてしまうのです。
そのため、6x6盤のオセロの完全解を求めるプログラムの整合性を、4x4盤のプログラムを使って検証することができます。なにしろ、4x4盤のオセロは1ミリ秒以内に解けますが、6x6盤はi7-3770Kのマシンで4264688秒、すなわち、ほとんど50日かかってしまいます。50日たってから間違いが見つかったら悲惨です。
ちなみに、4x4盤の解は後手白番の10目勝ち3、6x6盤は後手白番の4目勝ちです4。
通常のオセロ(8x8盤)は64マスを持っています。これに駒を置かれているのを1、置かれていないのを0で表現すると、オセロの局面は黒番と白番双方にそれぞれ64ビット(=8バイト)を与えれば局面が表現できることになります(厳密に言うと、これに加えてどちらの手番かを表わす変数が必要)。8バイトはuint64_t(unsigned long long)で表せますから、オセロはビット演算とたいへん親和性があるのです。
C++のプログラムは、全体としてはリスト1のような形になっています。盤のサイズに依存するクラス(構造体)のうち「struct B36」を、リスト2(関数定義は一部だけ)に示します。また、8x8盤(struct B64)と4x4盤(struct B16)の一部はリスト3に示します。
課題1は、Bnn(nn=16, 36, 64)とBitOpを、Rustで実装することです。
// 「...」は煩雑のため省略することを表しています(言語仕様ではありません)
struct B16{...}; //4x4盤に特有な定数とビット操作関数
struct B36{...}; //6x6盤(今回のメイン)
struct B64{...}; //8x8盤(本来の目的)
// [課題1] 2個のstatic関数を持つクラス(Bnnで定義されたビット操作関数を呼ぶ)
// T=B16, B36, B64
template <class T>
class BitOp {
public:
// 局面に対する候補手を求める
static uint64_t getCandidates(uint64_t, uint64_t);
// 打つ前の盤面を打ち手後の盤面に変更する
static int turnOver(int, uint64_t*, uint64_t*);
};
// [課題2] 計算の主体となるクラス(BitOp<T>の関数を呼ぶ)
// T=B16, B36, B64
template <class T>
class Board {
private:
//インスタンス変数
Nodelet initial;
...
public:
...
// 最初の局面を設定してcalcNode()を呼ぶ
// calcNode()の終了後に後処理
int getBestResult(
uint64_t bp = T::INITIAL_BP,
uint64_t wp = T::INITIAL_WP,
int turn = 0,
int alpha = -(T::CELLS + 1),
int beta = T::CELLS + 1
);
// 1局面を計算する(再帰的)
// 計算の核となる関数(BetOp<T>のstatic関数を参照する)
int calcNode(int *pTurn, uint64_t *pInturn, uint64_t *pOpponent,
int alpha, int beta, int pass);
...
};
struct B36 {
constexpr static int SIZE = 6;
constexpr static int CELLS = SIZE * SIZE;
constexpr static uint64_t MASK = 0x0000000FFFFFFFFF;
constexpr static uint64_t INITIAL_BP = 1081344;
constexpr static uint64_t INITIAL_WP = 2113536;
constexpr static int INITIAL_MOVE = 22;
constexpr static uint64_t RV_MASK0 = 0x000000079E79E79E;
constexpr static uint64_t RV_MASK1 = 0x000000003FFFFFC0;
constexpr static uint64_t RV_MASK2 = 0x000000001E79E780;
//4個のstatic関数
static uint64_t getUpward(int, uint64_t, uint64_t, uint64t);
static uint64_t getDownward(int, uint64_t, uint64_t, uint64t);
static uint64_t reverseUpward(int, uint64_t, uint64_t, int64_t, uint64_t);
static uint64_t reverseDownward(int, uint64_t, uint64_t, int64_t, uint64_t);
};
uint64_t B36::getUpward(int inc, uint64_t mask, uint64_t inturn, uint64_t opponent)
{
uint64_t w = opponent & mask;
uint64_t t = w & (inturn << inc);
t |= (w & (t << inc));
t |= (w & (t << inc));
t |= (w & (t << inc));
t |= (w & (t << inc));
return (t << inc);
}
...
struct B16 {
constexpr static int SIZE = 4;
constexpr static int CELLS = SIZE * SIZE;
constexpr static uint64_t MASK = 0x000000000000FFFF;
constexpr static uint64_t INITIAL_BP = 576;
constexpr static uint64_t INITIAL_WP = 1056;
constexpr static int INITIAL_MOVE = 11;
...
};
struct B64 {
constexpr static int SIZE = 8;
constexpr static int CELLS = SIZE * SIZE;
constexpr static uint64_t MASK = 0xFFFFFFFFFFFFFFFF;
constexpr static uint64_t INITIAL_BP = 34628173824;
constexpr static uint64_t INITIAL_WP = 68853694464;
constexpr static int INITIAL_MOVE = 37;
...
};
課題1のRustによる実装
Rustによる実装をリスト4に示します。Rustでは、盤面のサイズに依存する部分(trait BitOpBase)と共通部分(trait BitOp)をそれぞれのtraitに分けることで、とても明快な表現ができます。
明快な表現が可能である要因のひとつは、Rustのtraitでは「Associated Constants」を使用できることです。これは、C++にはなかった機能です。
リスト2で定義しているC++の構造体B36、およびリスト3に一部を示したB16とB64ですが、これらは同じ名前の定数と同じプロトタイプの関数を持っているというだけです。共通のインタフェース(完全仮想関数を含むクラス)を実装しているわけではありません。その原因は、C++では「仮想定数のようなもの」を持ったインタフェースを定義できないからです。
これに対して、RustのAssociated Constantsは定数の実装を要求します。このため、
impl<T: BitOpBase> BitOp for T {
のようにtrait境界を設定できるのです。C++より表現力が高いと言えるでしょう。C++に比べた評価は「◎」です。
//盤のサイズに依存する定数と関数を含むtrait(実際の定義はリスト5)
pub trait BitOpBase {
const SIZE : i32;
const CELLS : i32;
const MASK : u64;
const INITIAL_BP : u64;
const INITIAL_WP : u64;
const INITIAL_MOVE : i32;
const RV_MASK0 : u64;
const RV_MASK1 : u64;
const RV_MASK2 : u64;
fn get_upward(inc : i32, mask : u64, inturn : u64, opponent : u64) -> u64;
fn get_downward(inc : i32, mask : u64, inturn : u64, opponent : u64) -> u64;
fn reverse_upward(inc : i32, mask : u64, tmask : u64, inturn : u64, opponent : u64) -> u64;
fn reverse_downward(inc : i32, mask : u64, tmask : u64, inturn : u64, opponent : u64) -> u64;
}
//盤のサイズに依存しない関数を持つtrait
pub trait BitOp {
fn get_candidates(inturn : u64, opponent : u64) -> u64;
fn reverse(rmove : i32, pt : &mut u64, po : &mut u64) -> i32;
// 以下[課題3]に対応する関数(リスト9を参照)
...
}
// BitOpのうちBitOpBaseの定数と関数を参照する部分の実装
impl<T: BitOpBase> BitOp for T {
// 局面に対する候補手を求める
// inturn:手番の盤面
// opponent:相手番の盤面
// 戻り値:候補手の盤面(全候補手を盤面に配置する)
fn get_candidates(inturn : u64, opponent : u64) -> u64 {
let candidates : u64 =
T::get_upward(1, T::RV_MASK0, inturn, opponent)
| T::get_downward(1, T::RV_MASK0, inturn, opponent)
| T::get_upward(T::SIZE, T::RV_MASK1, inturn, opponent)
| T::get_downward(T::SIZE, T::RV_MASK1, inturn, opponent)
| T::get_upward(T::SIZE - 1, T::RV_MASK2, inturn, opponent)
| T::get_downward(T::SIZE - 1, T::RV_MASK2, inturn, opponent)
| T::get_upward(T::SIZE + 1, T::RV_MASK2, inturn, opponent)
| T::get_downward(T::SIZE + 1, T::RV_MASK2, inturn, opponent);
(!(inturn | opponent)) & candidates
}
...
}
use super::bitop::BitOpBase;
pub struct B36;
impl BitOpBase for B36 {
const SIZE : i32 = 6;
const CELLS : i32 = B36::SIZE * B36::SIZE;
const MASK : u64 = 0x0000000FFFFFFFFF;
const INITIAL_BP : u64 = 1081344;
const INITIAL_WP : u64 = 2113536;
const INITIAL_MOVE : i32 = 22;
const RV_MASK0 : u64 = 0x000000079E79E79E;
const RV_MASK1 : u64 = 0x000000003FFFFFC0;
const RV_MASK2 : u64 = 0x000000001E79E780;
//(改訂版で追加)実行速度が大幅に向上しました
#[inline]
fn get_upward(inc : i32, mask : u64, inturn : u64, opponent : u64) -> u64 {
let w : u64 = opponent & mask;
let mut t : u64 = w & (inturn << inc);
t |= w & (t << inc);
t |= w & (t << inc);
t |= w & (t << inc);
t |= w & (t << inc);
t << inc
}
...
}
課題2. クラスを引数としたテンプレートでクラスを記述する(インスタンス変数を含むクラス)
表題の表現が少し分かりにくいのですが、普通のクラスをtemplateで定義するだけです。ただし、テンプレートの引数が普通の型ではなくクラス(Rustではtrait)です。
課題2のRustによる実装
ところが、これが意外に方法がわかりませんでした。要は
struct Board<T> {
node_count : u64,
...
}
のように宣言したいのですが、ジェネリック引数Tがスカラー型ではなくtraitであるため、対応するクラス変数がないのです。そのためにコンパイルエラーが出てしまいます。
何とか見つけたのは、「std::marker::PhantomData」を使う方法です。結果として、リスト7のような形になりました。一応これで使えるのですが、なんだかしっくりきません。あまりにもテクニカルにすぎるような気がします。極めてよくあるパターンですから、リスト6のような形でもコンパイルエラーを出さないような仕様に変えてほしいものです。
評価が「◎」でなく「◯」なのは、これが理由です。
use std::marker::PhantomData;
...
pub struct Board<T> {
node_count : u64,
...
_marker : PhantomData<T>, //完全なダミー変数
}
impl<T: BitOpBase + BitOp> Board<T> {
pub fn new() -> Self {
Board{
node_count : 0u64,
...
_marker : PhantomData::<T> //幻の定数
}
}
pub fn get_best_result_with_ab(&mut self, bp : u64, wp : u64, turn : i32,
alpha : i32, beta : i32) -> i32 {
...
}
fn calc_node(&mut self, pturn : &mut i32, pinturn : &mut u64, popponent : &mut u64,
alpha : i32, beta : i32, current_pass : i32) -> i32 {
...
}
...
}
課題3. ビルトイン関数の実装
// [課題3] g++のビルトイン関数を呼ぶ
// 1であるビットの総数を求める
inline int bitcount(uint64_t m) {
return __builtin_popcountll((int64_t)m);
}
// 下位から数えて最初に1となるビットの位置を求める
inline int lsb(uint64_t m) {
return __builtin_ctzll((int64_t)m);
}
いままで示したC++のプログラムリスト中には出ていないのですが、Boardクラスの中でリスト8に示す2種類のビルトイン関数を使用しています5。この関数はgcc/g++独自のものですが、C++20では対応する関数が導入されています。ビルトイン関数は最終的にはCPUの1命令に解決されるため6、計算速度の向上に寄与することが期待できます。
このようなCPUのアーキテクチャに依存した関数が、Rustでも使えるのでしょうか?
下の表が答えです。これを使ってリスト9のように実装しました。Rustには何でもそろっているようですね。感心しました。
| gcc/g++ | C++20 | Intel CPU | Rust |
|---|---|---|---|
| __builtin_popcountll | popcount | popcnt | std::arch::x86_64::_popcnt64 |
| __builtin_ctzll | count_zero | tzcnt | std::arch::x86_64::_tzcnt_u64 |
pub trait BitOp {
...
// u64の全64bitのうち1であるbitの総数を求める
// cpuの組み込み関数をコールする
#[cfg(target_arch = "x86_64")]
fn bitcount(x: u64) -> i32 {
unsafe {
std::arch::x86_64::_popcnt64(x as i64)
}
}
#[cfg(target_arch = "x86_64")]
fn lsb(x: u64) -> i32 {
unsafe {
std::arch::x86_64::_tzcnt_u64(x) as i32
}
}
}
課題4. 実行性能
Rustと比較するべきは、数あるLLではなくC++です。利用される局面ではパフォーマンスが何よりも重要になるはずです。私は、よく考えられた仕様により生産性が向上することを考慮して、C++の50%の実行速度を基準に置きました。これ以上の性能があれば、C++の代わりにRustを使う局面が多くなると思います。
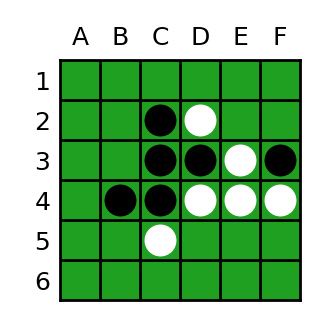
そこで、C++とRustの比較を行うわけですが、フルに計算すると50日かかってしまいますから、途中から始めます。図3は黒白双方が4手づつ打った局面で、次が黒の手番です。この局面が完全解の途中の局面であることは、フル計算の過程であらかじめ分かっています。
ちなみに、初手からこの局面までの手順はリスト10の「|」までです。
e4 c5 b4 e3 c2 d2 f3 f4|f5 b3
a3 c1 d5 e5 d1 e1 e2 a5 c6 a4
a6 e6 b5 b6 a2 b2 d6 f6 b1 a1
pa f2 f1
です。Rustのメインプログラムはリスト11です。ここで、「alpha」と「beta」という変数を使っています。これは「アルファ・ベータ法」というもので、囲碁や将棋のような「二人零和有限確定完全情報ゲーム」の解法には必須のアルゴリズムです。alphaとbetaは、このアルゴリズムの鍵となる変数です。
alpha と beta の値にも、フル計算で得られた値を使っています。その値を使わない場合には、5倍以上の計算時間が必要です。
fn main() -> Result<(), ()> {
let bp : u64 = 1753344;
let wp : u64 = 81854976;
let turn : i32 = 0;
let alpha : i32 = -6;
let beta : i32 = -2;
let mut board : Board<B36> = Board::<B36>::new();
let result : i32 = board.get_best_result_with_ab(bp, wp, turn, alpha, beta);
println!("Result = {}", result);
println!("initial = {}", board.get_initial());
println!("Final = {}", board.get_final());
println!("Moves = {}", board.get_move_list_string());
println!("Elapsed = {}", board.get_elapsed());
Ok(())
}
結果を以下に示します。
| Rustの計算時間 | C++の計算時間 | 性能比 |
|---|---|---|
| 755.4 sec (当初977.1 sec) | 725.8 sec | 96% (当初74%) |
C++に対する性能比は96%です。十分な性能です。
なお、Rustでは「--release」でコンパイルしています。また、「--target-cpu=native」のオプションをつけてコンパイルしても実行時間は全く変わりませんでした。Rustの「--release」は、かなりの水準まで最適化されているようです。
当初の計算ではC++との性能比が74%でした。これでも十分高速なのですが、まだ速くなるような気がしていたので、いくつかの観点から調査しました。その結果、性能比は96%まで向上しました。キーになったのは「インライン展開」です
インライン展開
(2021-03-02:追加)
記事を書いた当初の計算では、C++に対する速度比が74%でしたので、速度低下の原因を探ることにしました。
検証プログラムには、BitOpBaseというtrait(リスト4)にget_upward、get_downward、reverse_upward、reverse_downwardという、ビット操作のみで構成される関数があります。これらの関数は、C++においては、ほぼ1対1で機械語命令に対応します。そこで、速度の差がここにあるのではないかと考え、Rustのアセンブリ出力を見てみました。
リスト12は、get_upward関数の実装(リスト5参照)をアセンブリ出力したものです。全く無駄な部分がなく、綺麗にコンパイルされています。ところが、問題はこの関数の参照側にあったのです。
<bitop::b36::B36 as bitop::bitop::BitOpBase>::get_upward:
mov rax, rcx
mov ecx, edi
and rsi, rax
shl rdx, cl
and rdx, rsi
mov rax, rdx
shl rax, cl
and rax, rsi
or rax, rdx
mov rdx, rax
shl rdx, cl
and rdx, rsi
or rdx, rax
mov rdi, rdx
shl rdi, cl
and rdi, rsi
or rdi, rdx
mov rax, rdi
shl rax, cl
and rax, rsi
or rax, rdi
shl rax, cl
ret
get_upward関数は、BitOp traitのget_candidates関数から参照されています。この関数のアセンブリ出力を比較してみたとき気付いたのですが、C++ではget_upwardがインライン展開されていたのです。うかつでした。
get_upwardのように、機械語にほぼ1対1に変換されるような関数は、よほど長くならない限りインライン展開するべきなのです。ところが、最近のg++は面倒見がよくて、勝手にインライン展開してくれます。そのため、私はRustのコンパイルオプションに、明示的にインライン展開の指示が必要なことに気づきませんでした。
Rustのコンパイラは、指示がないとインライン展開しない方針のようです。これでは、関数呼び出しのオーバーヘッドが避けられません。早速、当該の4個の関数にインラインアトリビュート(#[inline])をつけてコンパイルしたところ(リスト5参照)、C++に対する速度比が74%から96%に改善しました。
追加比較. バイナリサイズ
(この項未完)
あとがき
長くなりました。もし、最後まで読んで頂けた方がおられましたら、たいへん感謝します。コードの詳細はGitHubをご覧ください。
最後にRustの改善を期待したいことを書いておきます。
- traitを引数としたジェネリックなstruct(リスト6)
- 関数のデフォルト引数
今回のテーマを実行してみて、Rustはとても良く出来ていると感じました。上の2項目以外ほとんど不満がありません。
変更履歴
2021-04-24: 検証に使用したOSの記述を追加しました
2021-03-02: Rustの検証プログラムを修正し、C++に対する性能比が74%から96%に改善しました。これに従い、記事の内容を修正しました
2021-02-04: 関連するコードをGitHubにアップロードしました
-
先手も後手も最善手を選択した場合の手順を求めること。最初に6x6盤の完全解を求めたのは www.feinst.demon.co.ukの記事が最初のようです(このページは既にアーカイブされてしまっています)。2004年ごろの計算でSGIを使って2週間かかったそうです。今回の計算(とはいえ、CPUは8年前のもの)では7週間かかっていますから、彼らの計算はとても速いといえます。当時のSGIのマシンは、スーパーと言われていたころだと思いますから、速いのも納得できます。なお、この記事はマス目の配置が我々と異なっています(左上をB2にしている)。また、初手の打ち方も違いますので、それを考慮して変換すると、今回の計算結果と完全に一致します ↩
-
これ以外にも、マスの数が偶数でさえあれば、盤のサイズはいくらでも拡張できます。 ↩
-
4x4盤は最後に連続パスで終了しているため、2目が空白です。駒数の差だけなら白番の8目勝ちですが、オセロのルールでは空白は勝者のものとされるため、白番の10目勝ちになります ↩
-
古いCPUとはいえ6x6盤で50日もかかるぐらいですから、8x8盤の完全解は計算できていません。ただ、人間よりはるかに強いプログラム同士の対戦結果から推測して、引分けになるのではないかと言われています ↩
-
使用しているg++のバージョンは8.3.0です。C++20仕様のビット操作関数が導入されるのは9.3からです。そのためリスト8では、C++20の関数ではなく、g++のビルトイン関数を使用しています ↩
-
Qiitaの2016年Advent Calendarにビット演算を扱った記事があります ↩