CUDAは、NVIDIAのGPUを使って並列計算を行うためのフレームワークである。しかし、CPUを使った普通の計算に比べて、手順がややこしく、必ずしも汎用的とは言えない。そのため、それを使いこなすには、様々なサンプルに適用してみて感覚を磨く以外に方法はない。この例も、そのひとつである。
ここでは、KdV方程式と呼ばれる非線形の偏微分方程式
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + \delta^2 \frac{\partial^3 u}{\partial x^3} = 0 \tag{1}$$
を、CUDAを使って解き、CPUを使った計算と性能を比較してみる。なお、検証を行ったホストは、CPUがi7-3770、GPUがGTX680である。また、使用したCUDAのバージョンは8.0である。
KdV方程式は、ソリトンを記述する方程式である。ソリトンは孤立波であって、どこまでも安定的な波である。線形の波動方程式では、孤立波は時間とともに広がってしまい安定的に存在することはできないから、物理的にソリトンの振舞いはとても興味深い。数学的にもKdV方程式は深く研究されていて、非線形方程式の理論を構築する端緒にもなっている。
KdV方程式を数値的に最初に解いたのは、ZabuskyとKruskalの論文である(以下Z&Kと呼ぶ)。ここでは、Z&Kの論文の手法を踏襲して、CUDAプログラムに落とし込みを行う。
KdV方程式の解法
周期的境界条件
KdV方程式において、変数$t$は時間を、変数$x$は位置を表わす。解は
$$ u = u(t,x) $$
と、時間と位置の2変数の関数である。Z&Kは、まず、位置方向に周期=2の周期的境界条件
$$ u(t,x+2) = u(t,x) $$
を適用した。数値計算では無限の空間で計算を行うことはできないから、周期的境界条件を要請することはとても多い。
位置と時間の離散化
次に、連続量のままでは数値的に解けないから、変数の離散化を行う。
$$ u_i^j = u(i\Delta{t},j\Delta{x}) \tag{2}$$
ここで、位置方向は周期的境界条件があるので、全部で$N$個の点だけを考える(多くの表記はZ&Kに従っているが、$N$の定義だけ異なる。Z&Kでは、点の個数は$2N$個である)。周期的境界条件は、
$$ u_i^{N} = u_i^0 $$
になる。ここで、空間メッシュは、$\Delta{x} = 2/N$である。
時間メッシュ$\Delta{t}$は、時間をどこまで計算するかによって、適宜決める必要がある。大きすぎると数値計算が発散し、小さすぎると計算時間が膨大になる。
漸化式
数値計算では、微分方程式を数列(2)に対する漸化式に変換する。Z&Kは、
$$u_{i+1}^j = u_{i-1}^j + 2\Delta{t}f_i^j \tag{3}$$
$$f_i^j = - \frac{1}{6\Delta{x}}(u^{j+1}_i + u^j_i + u^{j-1}_i)(u^{j+1}_i - u^{j-1}_i)\\
- \frac{\delta^2}{2\Delta{x}^3}(u^{j+2}_i - 2u^{j+1}_i + 2u^{j-1}_i - u^{j-2}_i) \tag{4}$$
を用いている。この表式は、$\Delta{t}$、$\Delta{x}$共に2次の精度である。(3)式は、$\{u_{i-1}^j\}_j$、$\{u_{i}^j\}_j$を用いて、$\{u_{i+1}^j\}_j$を計算する表式である。すなわち、各時刻($t=i\Delta{t}$)ごとのスナップショット$\{u_i^k\}_{k=0,N-1}$を時間順に、逐次的に求めることが(3)式の意味である。
なお、(3)式では、$i+1$のデータを得るために、$i$と$i-1$のデータが必要なのだが、第1ステップだけは、$i-1$のデータが無い。このため、以下のプログラム中では、第1ステップだけ($i=0$、$\{u_0^j\}_j$は初期条件)、
$$u_{i+1}^j = u_{i}^j + \Delta{t}f_i^j \tag{5}$$
を使用している(Z&Kが第1ステップでどんな表式を使ったかについては、論文中に記載がない)。
パラメータと初期状態
KdV方程式の解は、パラメータ$\delta$の値や初期状態によって、まったく異なる様相を示す。Z&Kは、パラメータとして
$$\delta = 0.022$$
初期状態として、
$$u(0,x) = \cos(\pi{x})$$
を選んでいる。この場合にKdV方程式の特徴的な様相が現れる、という主張をしている。
CPUバージョンのプログラム
漸化式(3)を解くための、プログラム断片を以下に示す。
doStepOnCPU()関数において、2次元数列に対する漸化式を解く。配列u[j]は、jが位置方向の添字を表わす。時間方向については、u[j]とum1[j]が時間方向の役割($u_{i-1}^j$、$u_{i}^j$、$u_{i+1}^j$)を交互に担っている。また、calculateDerivatives()関数は(4)式を計算する関数、setInitialCondition()は初期条件をu[j]にセットする関数である。
kdvpは、(4)式中の各項の係数を格納するクラスで、
$$kdvp.a = (\frac{1}{6\Delta{x}})(\frac{\Delta{t}}{\pi}), $$
$$kdvp.b = (\frac{\delta^2}{2\Delta{x}^3})(\frac{\Delta{t}}{\pi})$$
である。なお、(3)式中の$\Delta{t}$を係数に含めている。また、Z&Kでは$T_B=1/\pi$を時間の基準に選んでいるので、この計算では$1/\pi$を時間単位に選ぶこととし、係数に組み込んでいる。
/**
* KdV方程式の右辺f_i^jを計算する
* N: 位置方向の計算点の数
* uu: 従属変数(位置方向の数列)、N個の配列
* ff: 右辺(位置方向の数列)、N個の配列
* kdvp: 係数を格納するクラス
*/
void KdV2::calculateDerivatives(double *uu, double *ff) {
for(int j=0; j<N; j++) {
double p1 = uu[(j + 1)%N];
double m1 = uu[(j - 1 + N)%N];
double p2 = uu[(j + 2)%N];
double m2 = uu[(j - 2 + N)%N];
ff[j] = - kdvp.a * (p1 + uu[j] + m1) * (p1 - m1)
- kdvp.b * ((p2 - m2) - 2*(p1 - m1));
}
}
/**
* CPUを使う計算
* N: 位置方向の計算点の数
* u[j]: u_i^j、N個の配列
* um1[j]: u_{i-1}^j、N個の配列
* counter: 時間方向の計算度数
* nSteps: 計算度数の上限
* result: 結果を格納するクラス
*/
void KdV2::doStepOnCPU() {
if (counter == 0) {
calculateDerivatives(u, f);
double* ub = um1;
um1 = u;
u = ub;
for(int j=0; j<N; j++) {
u[j] = um1[j] + f[j];
}
calculateDerivatives(u, f);
counter = 1;
}
for(; counter<nSteps; counter++) {
double* ub = um1;
um1 = u;
u = ub;
for(int j=0; j<N; j++) {
u[j] += 2*f[j];
}
calculateDerivatives(u, f);
}
result.setAll(u);
}
GPUに対するプログラム
上記のdoSteoOnCPU()関数を、GPUを使用するように変更したのが、以下のdoStepOnGPU()関数である。この2つの関数は同じインタフェースを持っているので、簡単に計算時間を比較できる。これらのプログラムは、GitHubで公開している。
/**
* GPUから呼ばれる(__device__)インライン(__inline__)関数
*/
__inline__ __device__ double derivative(unsigned tid, int N, cnl::KdVParam kdvp, double* a) {
double p1 = a[(tid + 1)%N];
double m1 = a[(tid - 1 + N)%N];
double p2 = a[(tid + 2)%N];
double m2 = a[(tid - 2 + N)%N];
return - kdvp.a * (p1 + a[tid] + m1) * (p1 - m1)
- kdvp.b * ((p2 - m2) - 2*(p1 - m1));
}
/**
* CPUから呼ばれる(__global__)GPU上の関数
*/
__global__ void kdv2_step(long nSteps, int N, cnl::KdVParam kdvp, double* um1) {
unsigned tid = threadIdx.x;
double f;
// 共有メモリを割付
extern __shared__ double a[];
double s;
double sm1 = um1[tid];
//第1ステップ
//共有メモリに代入する。それぞれのスレッドが自分の担当する位置に振幅の値を代入するので、
//結果的に共有メモリの全エリアに代入が行われる。
//そのため、__suncthreads()で代入が完了するのを待っている
a[tid] = sm1;
__syncthreads();
//2軒両隣までの共有メモリを参照して、方程式の右辺を計算する。
//後に共有メモリへの代入があるため、__suncthreads()ですべての参照が完了するのを待つ
f = derivative(tid, N, kdvp, a);
__syncthreads();
a[tid] = s = sm1 + f;
__syncthreads();
f = derivative(tid, N, kdvp, a);
__syncthreads();
nSteps--;
for(int i=0; i<nSteps; i++) {
double sb = sm1;
sm1 = s;
a[tid] = s = sb + 2*f;
__syncthreads();
f = derivative(tid, N, kdvp, a);
__syncthreads();
}
um1[tid] = s ;
}
/**
* GPUを使う計算
* N: 位置方向の計算点の数
* u[j]: u_i^j、N個の配列
* gu[j]: u[j]に対応する、GPU上のグローバル配列
* counter: 時間方向の計算度数
* nSteps: 計算度数の上限
* result: 結果を格納するクラス
*/
void KdV2::doStepOnGPU() {
size_t unit = N * sizeof(double);
//GPU上のグローバルメモリを、double✕N個分確保する
double* gu;
checkCudaErrors(cudaMalloc((void**)&gu, unit));
//初期状態を入れた配列u[i]を、GPU上のメモリにコピーする
checkCudaErrors(cudaMemcpy(gu, u, unit, cudaMemcpyHostToDevice));
//GPUのグローバル関数
//グリッドサイズ=1
//ブロックサイズ=N
//共有メモリサイズ=double✕N
kdv2_step<<<1, N, unit>>>(nSteps, N, kdvp, gu);
//カーネルプログラムの実行終了を待つ(この場合は、後のcudaMemcpy()でブロッキングされるので、無くても良い)
cudaDeviceSynchronize();
//計算結果(GPUのグローバルメモリ)をシステムメモリにコピーする
checkCudaErrors(cudaMemcpy(result.head(), gu, unit, cudaMemcpyDeviceToHost));
//GPUメモリを開放する
checkCudaErrors(cudaFree(gu));
counter += nSteps;
}
CUDAプログラムの概略
ここで、CUDAプログラムの概略をまとめておく。CUDAでは、CPU側とGPU側を別々のコンピュータのようにみなして、CPU側をホスト、GPU側をデバイスと呼ぶ。これは、CPUとGPUが別々の筐体上に存在するような大規模システムを考慮しているからだろう。
カーネル関数の参照
デバイス上で動くプログラムをカーネル(またはカーネルプログラム)と呼ぶ。ホストからカーネルを呼ぶときに使用する関数の参照は、
関数名<<<グリッドサイズ,ブロックサイズ,共有メモリサイズ>>>(引数リスト)
のように記述する。共有メモリを使用しない場合は、共有メモリサイズを省略可能である。<<<...>>>は、関数定義や関数宣言では必要ない。あくまでも、参照の際にだけ必要な付加的記述である。関数定義や関数宣言では、そのかわりに__global__宣言が必要である。また、ホストから直接呼ばれないで、カーネルの中でのみ参照される関数は、__device__宣言が必要である。
並列処理とスレッド
デバイス上では、いくつものカーネルプログラム単位が並行して動くので、その単位をスレッドと呼ぶ。GTX680を例にとると、最大16384個のスレッドを同時に実行することができる。
ブロックとはスレッドの集合であり、1つのブロックにスレッドが何個含まれるのかをブロックサイズと呼ぶ。同じく、グリッドはブロックの集合であり、1つのグリッドにブロックが何個含まれるのかをグリッドサイズと呼ぶ。
何故、中間的なブロックというまとまりが存在するかについては、いくつかの理由があるが、最大の理由は、同じブロックに所属するスレッドが「同期できる」からである。
KdV方程式においては、ひとつの位置をひとつのスレッドに割り当てている。(4)式から分かるように、ひとつの時刻の計算において、前の時刻における2軒両隣りまでのデータを必要とする。従って、次の時刻の計算を始める前に、前の時刻の計算が終わっていなければならない。これがスレッドの同期である。
スレッドの同期を行うためには、
__syncthreads()
を挿入する。kdv2_step()関数の中では、共有メモリの参照と書込みの直後に同期を行っていることに注意して頂きたい。連続する参照や連続する書込みの場合は、それぞれの最後の処理の後に同期を行えばよい。
このように、KdV方程式では全てのスレッドを同期しなければならないため、ブロックを1個しか使えない。このため、N=256の場合には同時に実行できるスレッドは256個に止まり、最大16384個の1.6%しか利用できないから、あまり効率的な並列処理ではない。
なお、cudaDeviceSynchronize()は、全てのブロックの実行終了を待つために挿入しているが、そもそもブロック数が1個であるうえ、cudaMemcpy()でブロッキング(カーネルプログラムの終了を待つ)されるため、この場合は無くても構わない。
同期の問題
上でも述べたが、共有メモリへの書込みと参照が入れ替わるごとに同期を行う必要がある。困ったことに、同期が適切に行われていなくてもエラーは出ない。ただ、計算結果が正しくないだけである。そのため、手間であっても、同じ手順をCPUで行う関数をあらかじめ用意して、計算結果を比較することが大事である。
共有メモリとグローバルメモリ
カーネルで利用できるメモリには共有メモリとグローバルメモリがある。共有メモリを利用する方が遥かに高速であるが、利用できるサイズに制限がある。GTX680では、1ブロックあたり49152バイトの共有メモリが利用できる。KdV方程式では、ひとつの時刻におけるスナップショットを共有メモリに割り当てているので、N=256の場合、2048バイトの共有メモリを使用している。
ホストプログラムからカーネルへのデータの移行、またはその逆については、外部メモリを利用する必要がある。KdV方程式の場合では、初期条件を適用した、$t=0$のスナップショットのデータ$\{u_0^k\}_k$を、カーネルへ転送している。そのため、カーネルの呼び出しの前にグローバルメモリの確保(cudaMalloc)とホストメモリからデバイスメモリへのコピー(cudaMemcpy)が必要である。
計算結果である最後のスナップショットは、逆にデバイスメモリからホストメモリにコピーを行い、最後にメモリの開放(cudaFree)を行う。
エラー処理
cudaMalloc()、cudaMemcpy()、cudaFree()等の関数のエラーを捕捉するために、checkCudaErrors()という関数を利用している。この関数のヘッダファイルは、CUDAのサンプルディレクトリ以下に含まれている(/usr/local/cuda/samples/common/inc)。
threadIdx
threadIdxは、グローバルオブジェクトであり、その値はスレッドのIDを示す。本来のスレッドIDは3次元だが、この場合は1次元分だけしか使用していないので、threadIdx.xの要素だけが意味を持つ。この他に、blockIdxというブロックのIDを格納するオブジェクトもあるが、ここではブロックを1個しか使わないので意味はない。
threadIdx.xは、0からN-1までである。共有メモリの中でthreadIdx.x番の要素だけが、このスレッドの担当であり、書込みの責任を持っている。
extern __shared__
カーネル関数内で使用する共有メモリを宣言する。関数の参照の際に、スレッドの数だけのdoubleのエリアを宣言している。
共有メモリの代わりにグローバルメモリを使用しても良いが、メモリアクセスの速度が全く違うので、一般的には共有メモリを使う方が速い。ただし、キャッシュがうまくヒットしてグローバルメモリでも速くなる場合があるので、一概に断定することはできない。
計算結果
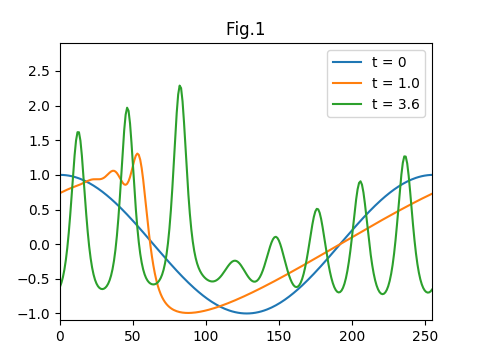
得られた結果を図1に示す。これはそれぞれ、初期状態、t=1.0、ならびに、t=3.6の振幅($u(t,x)$)である。ちょうど、Z&Kの図1に対応している。計算に影響がある時間メッシュはdt=1e-5を使用している。なお、ここで使用している時間の単位は、$T_B=1/\pi$であることにご注意頂きたい($T_B$という名前は、Z&Kで使われている)。
各時刻のスナップショットを繋いで動画にしたのが、図2である(mp4の方がファイルサイズが4分の1以下になるのだが、Qiitaにアップロード出来ないので、モーションGIFを使っている)。t=10までの結果をGIFアニメーションにしている。左からきた振幅の小さい波が、右側の振幅の大きい波とぶつかるも、すり抜けると元の形に戻っているのが分かる。また、時間がたっても波の形が崩れないのがソリトンの特徴である。
CPUとGPUの性能比較
位置方向メッシュ(N)を、N=256、N=512、N=1024の3種類に取り、CPUとGPUの計算時間を比較したのが下図である。全てt=(0,10)の計算であり、10回の試行による平均を取った。
| N | dt | GPU (GTX680) |
CPU (i7-3770) |
性能比 |
|---|---|---|---|---|
| 256 | 1e-5 | 0.827 sec | 2.330sec | 2.81 |
| 512 | 1e-5 | 1.078 sec | 4.624 sec | 4.29 |
| 1024 | 1e-5 | 1.676 sec | 9.161 sec | 5.47 |
| 256 | 1e-6 | 5.464 sec | 22.913 sec | 4.19 |
| 512 | 1e-6 | 7.949 sec | 45.656 sec | 5.74 |
| 1024 | 1e-6 | 13.779 sec | 91.080 sec | 6.61 |
Nの値は計算量に比例するため、CPUの計算時間はNの値に比例する。ところが、GPUでは、Nの値が4倍になっても計算時間が2倍程度にしかなっていない。これは、カーネルプログラムの並列度が大きくなるからである。一般にはブロックサイズとグリッドサイズが大きいほど、並列度が大きくなる。
ただし、カーネルプログラムが完全に並列に動作するわけではない。1つのブロックに含まれるスレッドであっても、完全に並列に動くのはワープ(Warp)と呼ばれる32個のスレッドだけである。異なったワープは同じ箇所の命令であっても異なるステップで実行されるため、ブロックサイズが大きくなることによるオーバーヘッドが存在する。そのため、スレッドが完全に並列であればNの値によらず実行時間が一定であるはずなのに、N=256とN=1024で2倍ほど時間がかかってしまう(この他にメモリ転送の時間の寄与もある。メモリ転送の時間はNに比例する)。
あとがき
KdV方程式をCUDAで解いてみた。位置と時間に対する偏微分方程式は、ある大きさのベクトルを逐次的に解いていくという、ある意味では並列処理に適した問題である。ただ、GPUの構造のためにブロックを1個しか使えないという制限があり、並列処理を限定的にしか使用できない。
そのような制限があっても、3倍から6倍程度のパーフォーマンスの改善がみられた。オーダーでの改善というわけにはいかなかったが、大量の数値計算をしなければならない場合には、これはやはり大きなことで、一定の意味がある。
ここで使った偏微分方程式の数値解法は、あくまでもZ&Kの時代の方法で、今となっては実用的ではない。現代では、$\Delta{t}$や$\Delta{x}$に対して4次の精度の表式(ここ使ったのは2次の精度)を使うのが普通である。ただ、その場合でも、GPUを利用することにより、やはり同じ程度のパーフォーマンスの改善を見込むことができる。
補遺
更新履歴
2018-05-09: 提示したプログラムをGitHubで公開した
2017-08-19: 章立ての変更、字句修正。表式(3)、(4)の導出について「補遺で説明する」ような記述があったが、削除した。これは別の記事で説明する予定