概要
時系列分析のライブラリを実際に使ってみました。
(statsmodels.api.tsa)
本記事は、筆者が時系列分析の理論を勉強してて、
理解を定着させるために書いた自己満の記事です。
分析概要
下記の(定常性を持つ)ARモデルでデータを作成し、
それをstatsmodelsライブラリ「ARMA」でパラメータ推定を行いました。
また、定常性を持つかをADF検定で行ってみました。
- 作成データ:下記モデルAR(1)で日単位のデータを作成(2018/1/1〜2019/12/31)
$y_{t}=2+0.8y_{t-1}$ - 学習モデル:定数項ありAR(1) ※ARMA(1,0)
- 学習方法:最尤推定
前提
-
ARモデル(自己回帰モデル Auto-Regression)
下記のように、時点tの値が過去直近時点(t-1)〜(t-p)の値の線型結合で表されるモデル。
$u_{t}$は誤差項であり、ホワイトノイズ(平均0の正規分布)。
(t-p)までで表される場合、AR(p)モデルと表記する。
今回はAR(1)モデルでデータを作成し、AR(1)モデルでパラメータ推定を行う。
$y_{t}=c+a_{1}y_{t-1}+a_{2}y_{t-2}+\ldots +a_{p}y_{t-p}+u_{t}$ -
定常性
「全時点において、平均が一定で、k時点前との共分散がkにのみ依存する」場合、
その時系列は「定常性を持つ」という。
今回の分析対象であるAR(1)モデルの場合、
定常性を持つ条件は下記の通りである。
「$y_{t}のモデル式における、y_{t-1}$の係数$a_{1}$ が $|a_{1}| < 1$を満たす。」 -
DF検定
単位根検定と呼ばれる検定の一つ。
対象の時系列をAR(1)と仮定し、
(帰無仮説を「単位根である」とし)
対立仮説を「定常性である」として行う検定。
検定量は標準正規分布。 -
ADF検定(拡張DF検定)
DF検定がAR(1)のみであるのに対し、
それを拡張させ、AR(p)でも適用できるようにした検定。
DF検定と同様に、
対立仮説は「定常である」であり、
検定量は標準正規分布。
分析詳細(コード)
1. ライブラリインポート
import os
import pandas as pd
import random
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import display
import statsmodels.api as sm
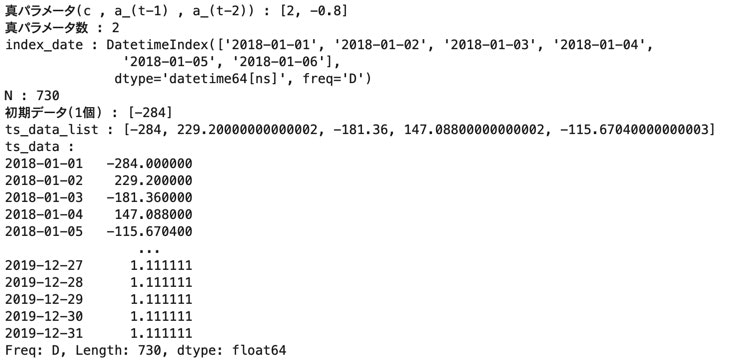
2. データ作成
データ;ts_data
# 真パラメータ (定常にするため全て1未満)
params_list = [2 , -0.8]
params_num = len(params_list)
print("真パラメータ(c , a_(t-1) , a_(t-2))" , ":" , params_list)
print("真パラメータ数" , ":" , params_num)
# 時系列データ作成
index_date = pd.date_range('2018-01-01' , '2019-12-31' , freq='D')
N = len(index_date)
init_y_num = params_num - 1
init_y_list = [random.randint(-1000 , 1000) for _ in range(init_y_num)]
print("index_date" , ":" , index_date[:6])
print("N" , ":" , N)
print("初期データ({}個)".format(init_y_num) , ":" , init_y_list)
ts_data_list = list()
for i in range(N):
if i < init_y_num:
ts_data_list.append(init_y_list[i])
else:
y = params_list[0] + sum([params_list[j+1] * ts_data_list[i-(j+1)] for j in range(params_num - 1)])
ts_data_list.append(y)
print("ts_data_list" , ":" , ts_data_list[:5])
ts_data = pd.Series(ts_data_list , index=index_date)
print("ts_data" , ":")
print(ts_data)
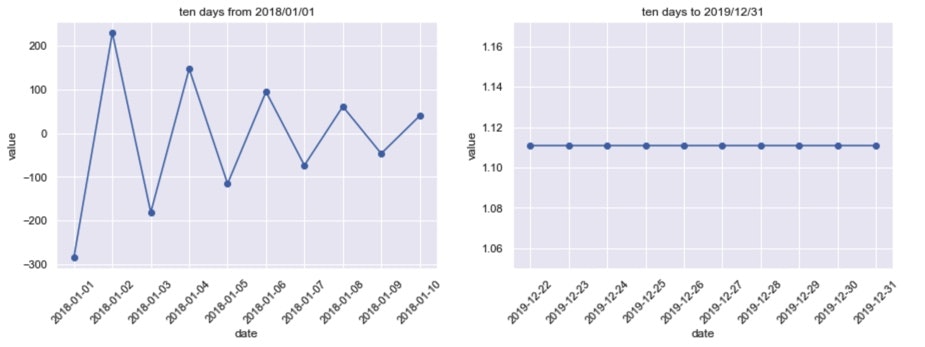
3. グラフ化(折れ線)_データ確認
# グラフ作成
fig = plt.figure(figsize=(15 ,10))
data = ts_data[:10]
ax_1 = fig.add_subplot(221)
ax_1.plot(data.index , data , marker="o")
plt.title("ten days from 2018/01/01")
plt.xlabel("date")
plt.ylabel("value")
plt.xticks(rotation=45)
data = ts_data[-10:]
ax_2 = fig.add_subplot(222)
ax_2.plot(data.index , data , marker="o")
plt.title("ten days to 2019/12/31")
plt.xlabel("date")
plt.ylabel("value")
plt.xticks(rotation=45)
plt.show()
4. ARモデル学習
下記3種のデータでモデル学習し、結果を確認。
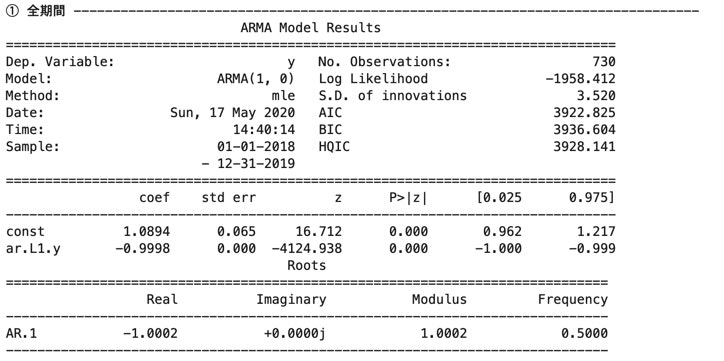
① 全期間(2018/1/1 ~ 2019/12/31)
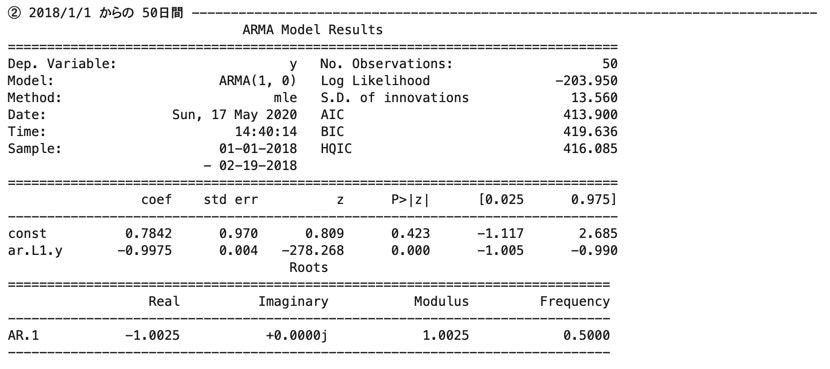
② 2018/1/1 からの 50日間
③ 2019/12/31 までの 50日間
# AR学習結果_学習データ① (全期間)
print("① 全期間" , "-" * 80)
data = ts_data
arma_result = sm.tsa.ARMA(data , order=(1 , 0)).fit(trend='c' , method='mle')
print(arma_result.summary())
print()
# AR学習結果_学習データ② (2018/1/1 からの 50日間)
print("② 2018/1/1 からの 50日間" , "-" * 80)
data = ts_data[:50]
arma_result = sm.tsa.ARMA(data , order=(1 , 0)).fit(trend='c' , method='mle')
print(arma_result.summary())
print()
# AR学習結果_学習データ③ (2019/12/31 までの 50日間)
print("③ 2019/12/31 までの 50日間" , "-" * 80)
data = ts_data[-50:]
arma_result = sm.tsa.ARMA(data , order=(1 , 0)).fit(trend='c' , method='mle')
print(arma_result.summary())
print()

…

①と②について係数(coef)を比較すると、
定数項(const)と$y_{t-1}$の係数(ar.L1.y)共に、
①の方が真のモデルに近い。
③に関してはログにて「対象時系列は定常性を持たない。定常性の時系列を入力すべき。」と出力された。
①〜③の結果より、
始めの時点の方が後の時点に比べ、上手くモデルにフィット出来ている形になった。
何故だろう?
5. ADF検定
4.と同様のデータ①〜③について、ADF検定を行う。
P値を確認し、どれ程の有意水準で帰無仮説を棄却する形になるか確認。
※対立仮説:対象時系列は定常性を持つ。
# AR学習結果_学習データ① (全期間)
print("① 全期間" , "-" * 80)
data = ts_data
result = sm.tsa.stattools.adfuller(data)
print('value = {:.4f}'.format(result[0]))
print('p-value = {:.4}'.format(result[1]))
print()
# AR学習結果_学習データ② (2018/1/1 からの 50日間)
print("② 2018/1/1 からの 50日間" , "-" * 80)
data = ts_data[:50]
result = sm.tsa.stattools.adfuller(data)
print('value = {:.4f}'.format(result[0]))
print('p-value = {:.4}'.format(result[1]))
print()
# AR学習結果_学習データ③ (2019/12/31 までの 50日間)
print("③ 2019/12/31 までの 50日間" , "-" * 80)
data = ts_data[-50:]
result = sm.tsa.stattools.adfuller(data)
print('value = {:.4f}'.format(result[0]))
print('p-value = {:.4}'.format(result[1]))
print()
全て検定値(value)が絶対値的にとても大きく、
P値(p-value)が0.0になっている。
有意水準を1%にしたとしても、
①〜③全て、帰無仮説が棄却される形となった。
(全てp値が0.0であり、比較的意味の無い比較かもしれないが、)
検定量の絶対値を比較すると、
① > ② > ③
であり、(データが完全にAR(1)なので)
ADF検定の結果としても始めの時点の方がより正しく評価されている感じになった。
まとめ
モデル学習結果とADF検定より、
始めの時点の方が正しく評価される形であった。
特に③のモデル学習結果については、全くの想定外であった。
何故そのような結果になったのか、因果関係について筆者はまだ理解出来ていない。
勉強を続けていくうちに分かればいいなと思っている。