【論文紹介】地味にすごいSqueeze and Excitation Networks

この記事について

この記事は2017年の論文Squeeze-and-Excitation Networks[1]について、紹介していきます。

イギリスのOxford大学と、中国のChinese Academy of Scienceによる論文で，

imageNetのコンテスト(ILSVRC)で前年より25%精度を向上させ、数あるモデルの中から2017年の1位を獲得したSENetを基にしています．

この論文は、今まで十分に考慮されていなかった、チャンネル間の相関を明示的に取り除くことで、2017年の1位を叩き出しました。比較的少ないパラメタで1%近く向上させ，かつ，どんなモデルにも適用可能ということで，強力なツールです．

コード

コードだけ見たい人はこちらから!

titu1994さんのKerasでの実装
moskomuleさんのPyTorchの実装
筆者によるCaffeでの実装

モデル

モデルのアイデア

筆者は，多変量解析における多重共線性(Multi Collinearity)と呼ばれる問題を意識して，モデルを組んでいると思います．

多重共線性は，説明変数間に相関がある際に，決定係数が相関がない場合に比べて大きくなるという現象がみられ，悪影響を及ぼします．

有効な対策として，より影響が弱い説明変数を取り除くことが行われます．
それを実装したのが，SENetです．

##モデルの中身
このSENetは，全体のArchitectureというより，一部のBlockを改善・提案しています．

このSE Blockは下図のようになっています．

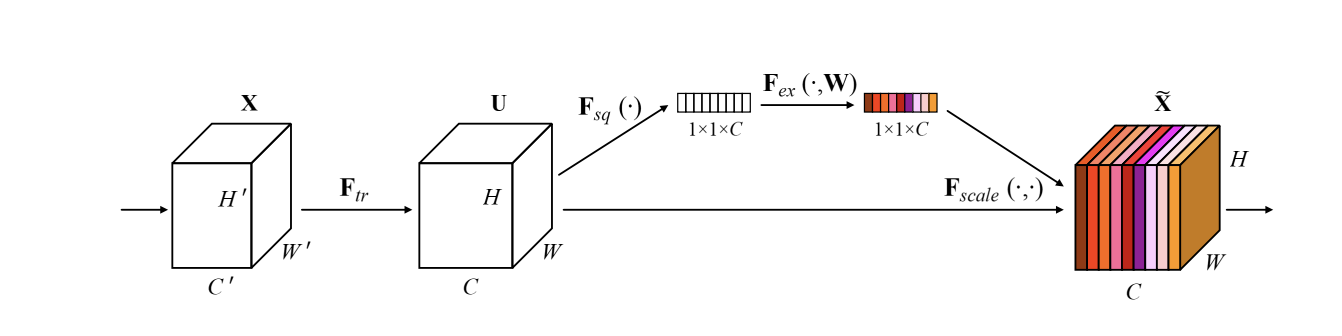
{F_{tr}} : Original \\
{F_{sq}} : Squeeze\ Operation \\ 
{F_{ex}} : Excitation\ Operation \\

上のSqueeze OperationとExcitation OperationがSE Blockの中身になります．

Squeeze Operationは，全体の特徴分布を見るために，チャンネルごとに，特徴をGlobal Average Pooling[2]で，凝縮(Embeddding)しています．

次に，Excitation Operationで，チャンネルごとの重み・荷重を出すために，2層のNNを通して，チャンネル間の相関を計算しています．

最後に，得られた重みを下のチャンネルに掛けることで，再度，チャンネルをスケーリングして，チャンネル間の相関を取り除いた特徴マップを生成しています．

実装のポイント

実装は下図です．

パッと見た感じだと，めちゃくちゃシンプルですが，

Squeeze Operationは一番シンプルなGlobal Average Poolingを用いているが，筆者曰く，より効率の良い空間情報を抽出できるものがあれば，性能が上がるのではと書いてました．しかし，実行時間とのトレードオフだと思います．

Excitation Operationでは，Inceptionなどで用いられる1x1Convと，全結合層を入れています．

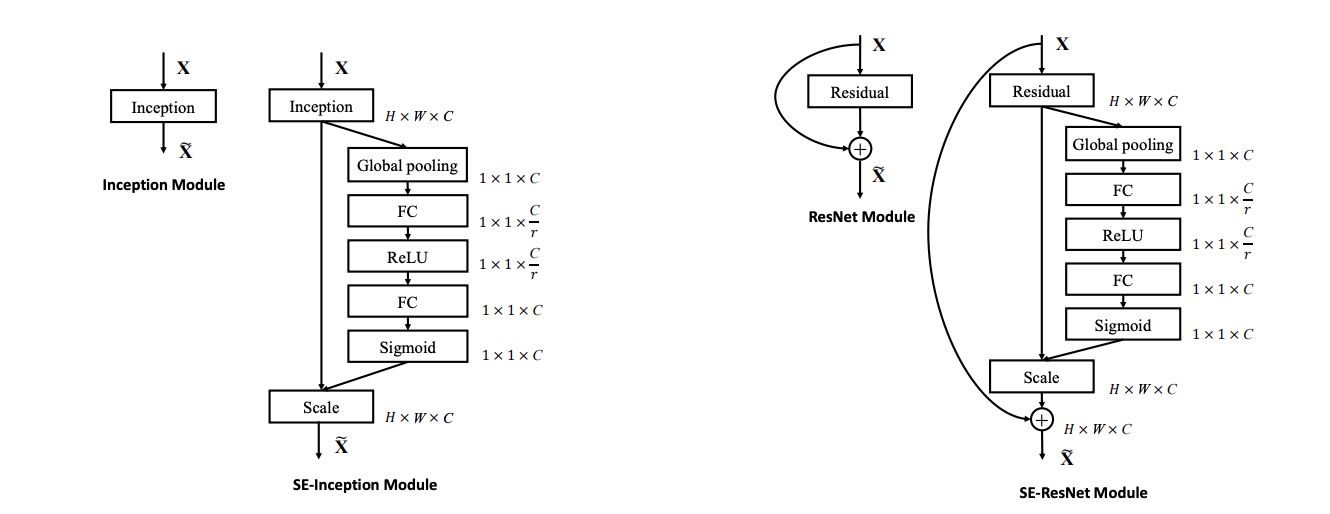
これらを，それぞれのModuleの最後に組み合わせていくのが基本です．
下の図は，ResNetとResNeXtの実装です．

###パラメタ数
上の図のように，全てのModuleにSE Blockを入れると10％増になるのですが，
最終層は効果が薄く(<0.1%)，最終層のModuleのSE Blockを取り除くと，4%増で済むようです．

Pytorch

torch-senet.py

class SELayer(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y.expand_as(x)

Pytorch Issueにあるように、Global Average Poolingにちょっと注意が必要です。

Tensorflow

tf-senet.py

from tensorflow.keras import layers
import tensorflow.keras.backend as K
 
def squeeze_excite_block(tensor, ratio=16):
    input_feature = tensor
    channel_axis = 1 if K.image_data_format() == "channels_first" else -1
    filters = init._keras_shape[channel_axis]
    se_shape = (1, 1, filters)

    se = GlobalAveragePooling2D()(input_feature) 
    se = Reshape(se_shape)(se) 
    se = Dense(filters // ratio, activation='relu', kernel_initializer='he_normal', use_bias=False)(se)
    se = Dense(filters, activation='sigmoid', kernel_initializer='he_normal', use_bias=False)(se)

    if K.image_data_format() == 'channels_first':
        se = Permute((3, 1, 2))(se)

    x = multiply([init, se])
    return x

最終結果

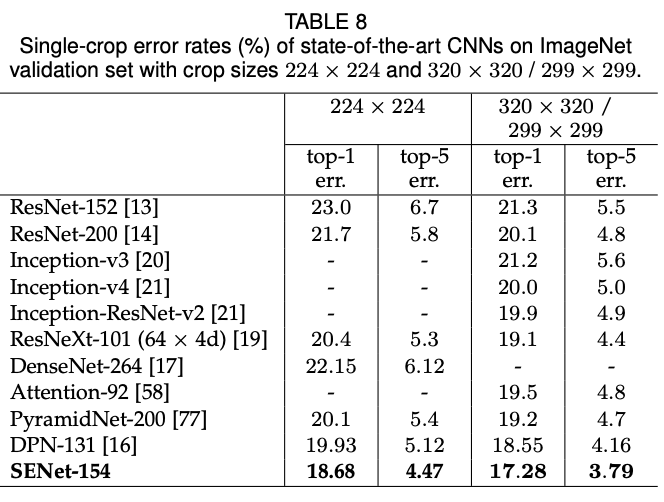
ImageNetの2017のコンペティションでベストの結果を出しています．
ResNeXtに，複数のスケールと複数のCroppingの戦略を用いて，複数モデルの平均を取っています．
結果はそれぞれの大きさのクロップされた画像に対するAccuracyの比較．

様々な実験

一番面白かった議論

複数の異なるクラス(金魚，パグという犬，飛行機，崖)でlayerごとのSENetの役割を，活性化関数の活性化の具合で比較し，浅いレイヤーでの役割と，深いレイヤーでの役割が異なることを言及しています．

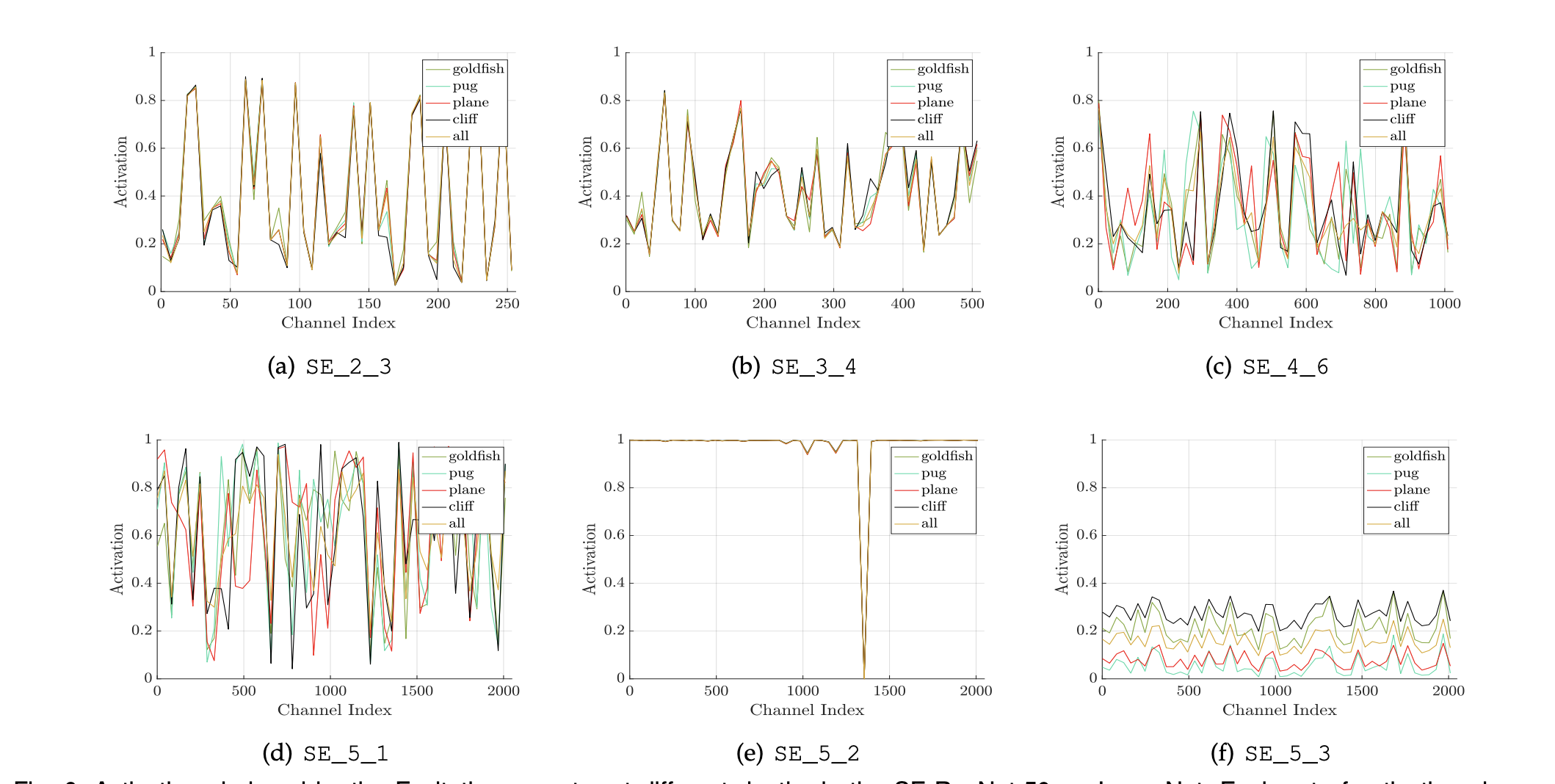
すなわち，浅いレイヤー(SE_2_3)では，特徴マップがクラスごとに共有されるため，よく似た活性化を表しています．
それに対して，深いレイヤー(SE_5_3)に対しては，特徴マップがクラス特有のものになっており，活性化関数はクラスによって活性化のは異なります．したがって，このネットワーク全体を通して，SE Blockの効果は蓄積されていくという風に筆者は締め括っています．

他にも，以下のような実験をしているのですが，興味があればぜひ，論文を一読ください．

• SE Blockのどれくらい圧縮するかのパラメタrの最適な値 -> 16が最強
• Squeeze OperationのGlobal Average PoolingとGlobal Max Poolingの比較 -> GAPが良さそう
• Excitation Operationの最適な活性化関数 -> sigmoidが良さそう
• SE Blockをどこに置くか -> 前や，並列にするもの同程度に効果的
• 全体のどこにSE Blcokを置くとより効果的か -> どれもプラスの効果で，組み合わせたものがベスト

感想

応用範囲が広いのも納得でき，Squeeze OperationのGlobal Average Poolingのところも，Excitation Operationの1x1 ConvとNNの部分もさらなる改善ができそう．

引用

• (論文)Squeeze-and-Excitation Networks
• (論文)Network in Network　GlobalAveragePoolingと1x1Convを導入