はじめに
GRAPH-BERTの論文を読んだので簡単に内容をまとめておきたいと思います。
論文: GRAPH-BERT: Only Attention is Needed for Learning Graph Representations
公式リポジトリ: https://github.com/jwzhanggy/Graph-Bert
注意事項として、必ずしも私が正しい理解をできている保証はありません。論文も公式実装も易しめなので気になった方は公式をご覧ください。
論文概要
GRAPH-BERTとは、**グラフデータをBERTで学習しようというGraph Neural Network(GNN)**です。
GRAPH-BERTはBERTに倣った以下のアーキテクチャをグラフデータに関して適用し、グラフノードのEmbeddingの自動獲得や、ノード分類タスクでの精度向上・学習効率向上を実現しています。
- Transformerを複数層重ねたEncoderを使う
- ラベル(教師データ)を用いずにモデルの事前学習を行う
- ラベルあり学習やタスク指向のファインチューニングを可能な構造にしている
またGRAPH-BERTは、グラフ全体から、リンクを持たない局所的なサブグラフ(linkless subgraph batching)群の構成に変換するアルゴリズムを考案し、サブグラフを入力コンテキストとして学習することで、GNN特有の問題(※1)を回避したとしています。
(※1)グラフはリンクに依存するため、ミニバッチ学習が困難、層の深さがある限界まで達するとパフォーマンス低下(suspended animation problem や over-smoothing problem)、等の問題がGNNあるあるだそうです。
GRAPH-BERTは具体的には「Transformerを50層重ねて深層にしてもパフォーマンスは落ちなかった」と報告しています。
データセット
paperの引用関係を表すグラフデータセット3種類(cora、citeseer、pubmed)を公式では使用しています。
どのようなデータ構造かについて以下簡単に説明します。
※公式リポジトリにも説明書きがありますので、そちらを読んだ方が早いかもしれません。
データセットはノード情報とリンク情報で構成されます。グラフ数=1のグラフデータを表していて、全体で1つのグラフを構築します。
- ノード
- 1ノードが1つのpaperを表しており、各ノードには特徴量とラベルが付与されている。
- 特徴量:各paper内で登場する語彙のBag-of-Wordsベクトル。語彙は数千程度まで削減済み。
- ※ノードが画像のデータセットだったら画素情報などでもOK。基礎的な特徴量ベクトル。
- ラベル:そのpaperの分野クラス。
- リンク
- paper間の引用・被引用関係を表している。citing paper → cited paper、という有向エッジ。
モデルアーキテクチャ
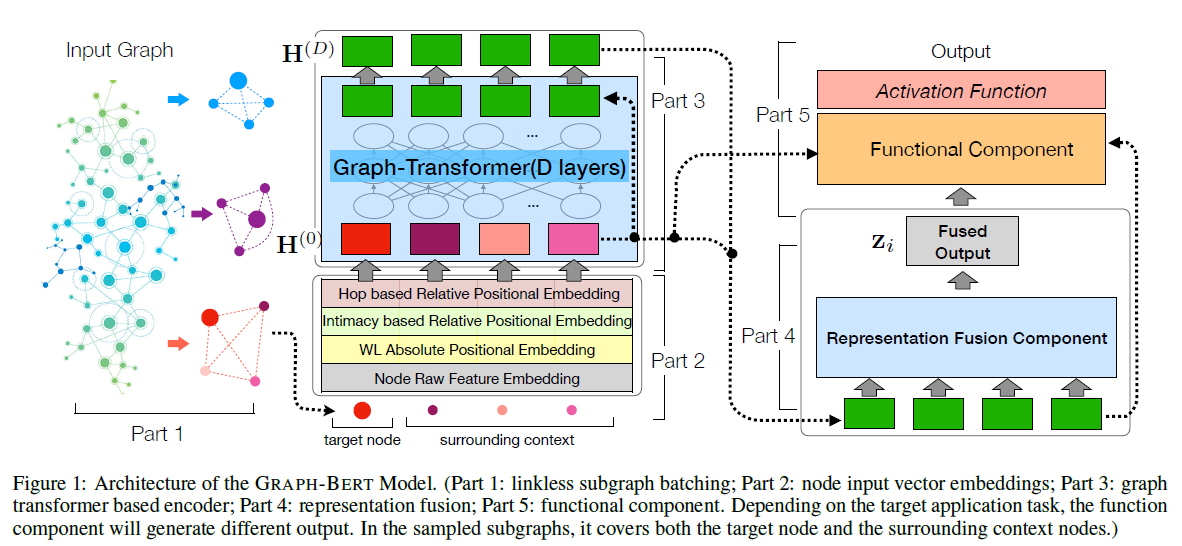
モデルアーキテクチャのキモは何といってもサブグラフとNode Embedding層であり、この考案がグラフデータをTransformer層に入力するための重要な工夫・テクニックと言えるでしょう。引用したFigure 1のPart 1と2の部分ですね。
サブグラフ(グラフバッチ)
本論文ではグラフの親密度行列(Intimacy Matrix)$\mathrm{S}$を定義し、これに基づいたアルゴリズムでサブグラフをサンプリングしています。全ノードの集合を$\mathcal{V}$とし、親密度行列を$\mathrm{S}^{|\mathcal{V}| \times |\mathcal{V}|}$としたとき、$\mathrm{S}(i, j)$はノード$v_i$と$v_j$間の親密度スコアを表します。
$\mathrm{S}$の定義はページランクアルゴリズムがベースとなっていますが、詳細は省きます。
各ノード$v_i \in \mathcal{V}$に対し親密度スコアが上位$k$個のノードを選択し、親密度が高い順に並べたものを「$v_i$の学習コンテキスト」とみなしてサブグラフ$g_i$と定義します。これを全ノードに対して実施し、サブグラフ群 $\mathcal{G} = \{ g_1, g_2, \cdots, g_{|\mathcal{V}|} \}$を獲得します。
サブグラフ$g_i$はいわゆるノード群ですが、リンクを持たないグラフ(linkless subgraph)とみなすことができます。
サブグラフ$g_i$=ノード$v_i$の学習コンテキストですので、$g_i$と$v_i$は一対一で対応しています。
このサブグラフ情報を利用しながら、下記のPositional Embeddingを作成していきます。
Node Embedding
各ノードを4種類のEmbeddingに埋め込んでいます。
4種類のEmbeddingとは、ノードの特徴量をほぼそのまま使うEmbeddingと、グラフやサブグラフ内におけるノードの位置情報を埋め込む3種類のPositional Embeddingです。
学習を行うとき、入力シーケンス(コンテキスト、自然言語でいう一文)はサブグラフ内のノードを並べたものになります。
よって「各ノードを埋め込む」とは、「入力コンテキスト$g_i$内におけるノード$v_j$のふるまいを埋め込む」操作になります。Figure 1のtarget nodeが$v_i$、surrounding contextがそれぞれ$v_j$にあたります。
Emebeddingは簡単にまとめると下記の表のイメージです。
Transformer層のhidden_sizeが$d_h$のとき、各Embeddingはどれも$d_h$次元であり、最終的にはこれらのEmbeddingをsumして次のTransformer層へ渡しています。
| Embedding名 | 概要と意図 |
|:-----------------|:-------------------|:------------------|
| Node Raw Feature Embedding | データセットとして与えられているノード特徴量。ベースとなる。 |
| Weisfeiler-Lehman Absolute Role Embedding | グラフ全体に対する構造的役割。大域的な特徴。 |
| Intimacy based Relative Positional Embedding | サブグラフ内での順序位置。局所的な特徴。 |
| Hop based Relative Distance Embedding | サブグラフ内のノード間の全体グラフでの距離。大域と局所のつなぎ的役割。 |
詳細を以下記述します。興味のない方は読み飛ばしていただいて大丈夫だと思います。
Node Raw Feature Embedding
\mathrm{e}_j^{(x)} = \mathrm{Embed} (\mathrm{x}_j) \in \mathbb{R}^{d_h \times 1}
入力データセットに記述されているノードの特徴量 $\mathrm{x}_j$ をシンプルに$d_h$次元に埋め込みます。全結合層に掛けるでもよし、画像ならCNNに掛けるでもよし、です。
Weisfeiler-Lehman Absolute Role Embedding
\begin{align}
\mathrm{e}_j^{(r)} &= \mathrm{Position \mathrm{-} Embed} (\mathrm{WL}(v_j)) \\
&= \Biggl[ sin \Biggl( \frac{\mathrm{WL}(v_j)}{10000^{\frac{2l}{d_h}}} \Biggr), cos \Biggl( \frac{\mathrm{WL}(v_j)}{10000^{\frac{2l+1}{d_h}}} \Biggr) \Biggr]_{l=0}^{ \bigl[\frac{d_h}{2} \bigr]} \;\; \in \mathbb{R}^{d_h \times 1}
\end{align}
Weisfeiler-Lehmanアルゴリズムに従ってグラフデータ全体における構造的な役割のラベルをノードに付与し、それを埋め込みます。大域的な情報のEmbeddingです。
ラベリング$\mathrm{WL}(v_j)$は、サブグラフは全く関係なく、グラフ全体から各ノードに対して事前算出されます。
Weisfeiler-Lehman Graph Kernelの参考:
Learning Convolutional Neural Networks for Graphs - Slide Share
※Positional Embedding(3種類とも)の算出式で出てくる$\mathrm{Position \mathrm{-} Embed} ( \cdot )$は、おそらくTransformerの論文で登場するPositional Encodingと同じです。ベクトル中の位置を明示的にエンコーディングして表現します。具体的にはsinとcosを$l$回計算したものを並べて$d_h$次元ベクトルにしてしまおうという関数になります。
Intimacy based Relative Positional Embedding
\mathrm{e}_j^{(p)} = \mathrm{Position \mathrm{-} Embed} (\mathrm{P}(v_j)) \in \mathbb{R}^{d_h \times 1}
サブグラフ$g_i$内のノードを$v_i$に対する親密度スコアが高い順に整列させ、その中におけるノード$v_j$の位置を埋め込みます。局所的な情報のEmbeddingです。
※おそらく${P}(v_j)$は、$v_i$に近い$v_j$から$1,2,3,...,k$となります。
Hop based Relative Distance Embedding
\mathrm{e}_j^{(d)} = \mathrm{Position \mathrm{-} Embed} (\mathrm{H}(v_j;v_i)) \in \mathbb{R}^{d_h \times 1}
$v_j$から$v_i$へのホップ距離$\mathrm{H}(v_j;v_i)$を埋め込みます。このホップ距離は、サブグラフ内ではなく元のグラフ(グラフ全体)を用いて数えます。
大域的な情報であるAbsolute Role Embeddingと局所的な情報であるIntimacy based Relative Positional Embeddingのバランスを取るためのEmbeddingと言えます。
Transformer層
一般的なBERTと同様のTransformer層です。公式実装はhuggingface/transformersのBertEncoderを使用しています。
import torch
from transformers.modeling_bert import BertPreTrainedModel, BertPooler
from code.MethodBertComp import BertEmbeddings, BertEncoder
BertLayerNorm = torch.nn.LayerNorm
class MethodGraphBert(BertPreTrainedModel):
data = None
def __init__(self, config):
super(MethodGraphBert, self).__init__(config)
self.config = config
self.embeddings = BertEmbeddings(config)
self.encoder = BertEncoder(config)
self.pooler = BertPooler(config)
self.init_weights()
最終層
Figure 1のPart 4に示されるように、まずはTransformer層の出力をRepresentation Fusion Componentに通してFused Outputを計算します。Fusionはシンプルに、出力された$k+1$個のベクトルの平均をとるだけです。
その後、Part 5に示されるように、タスクに合わせて全結合層などに通して最終出力とし、loss計算などを行います。
この全結合層を変えることでタスク指向のファインチューニングが可能なアーキテクチャになっています。
学習方法
教師なし事前学習タスク
論文で提案しているGRAPH-BERTの教師なし事前学習は以下の2つです。
- ノード特徴復元(Node Raw Attrubute Reconstrucstion)
- ノード再構成(Graph Structure Recovery)
教師ありファインチューニングのタスク
事前学習済みのモデルからファインチューニングするにしろ、事前学習していないモデルを最初から学習させるにしろ、教師あり学習のタスクは以下の2つです。
- ノード分類(Node Classification)
- ノードクラスタリング(Graph Clustering)
精度
事前学習なし+教師あり学習
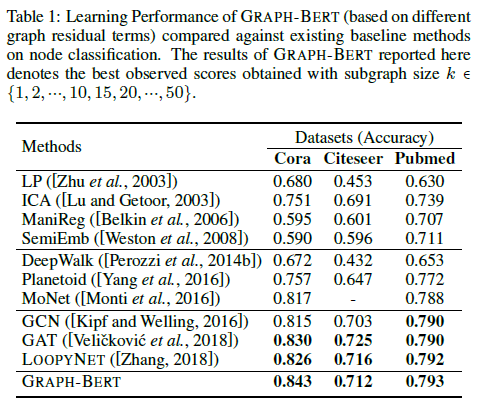
GRAPH-BERTは事前学習を行わなくても、その構造自体からグラフに対する有効性はあります。ということを示すため、事前学習なしの教師あり学習結果がTable 1に示されています。
ノード分類タスクにおいてCora, Citeseer, Pubmedデータセットでほぼほぼ既存のベースライン(SOTA含む)よりも良い精度を達成しています。Citeseerについてはちょっと低いですが。
事前学習あり+ファインチューニング
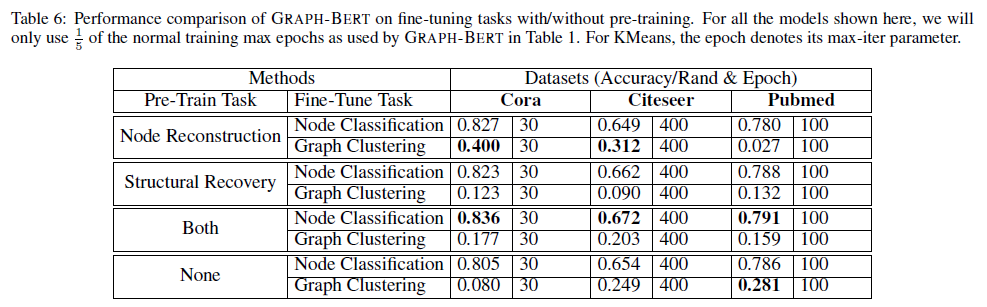
事前学習+ファインチューニングの効果については、Table 6にまとめられています。
ファインチューニングの有効性に関する議論
論文の5.4節では以下のような言及がなされています。早く学習が収束するための事前学習という印象です。
- 十分なEpoch数で教師あり学習するならば、事前学習の有無にかかわらずGRAPH-BERTは良い精度を出す。
- 教師あり学習を$\frac{1}{5}$のEpoch数にした場合は、事前学習を行うことにより、(事前学習なし+元のEpoch数で学習する場合と比べて)遜色ない精度になる。つまり良い初期解を事前学習により与えることが可能である。
- 事前学習を2タスクとも実行すれば、事前学習なしの場合(ただし十分なEpoch数の$\frac{1}{5}$)よりも精度は高くなる。
ここでTable 1とTable 6を比較すると、事前学習+少ないEpoch数でのファインチューニングよりも、事前学習なし+十分なEpoch数での教師あり学習の方が、精度は高いことが窺えます。
同じノード分類タスクでの精度をまとめると以下の表のようになります。
| Methods of GRAPH-BERT | Cora acc | Citeseer acc | Pubmed acc |
|---|---|---|---|
| 事前学習なし、教師あり学習のみ | 0.843 | 0.712 | 0.793 |
| 事前学習あり+ファインチューニング(2タスクとも実施) | 0.836 | 0.672 | 0.791 |
個人的な意見
果たして事前学習は必要なのか?
事前学習+ファインチューニングについての性能は、「早期に収束できるような良い初期解を、事前学習により与えることが可能である」というもの。
逆に言えば、引用した5.4節の前半でも触れられていますが、十分なEpoch数学習するならば事前学習する必要は特にない、ということです。
仮に多様なタスクに対して事前学習でかなり精度が上がるのであれば、事前学習+ファインチューニングも意味があると思いますが、本論文を読む限りそこまで意味があることとは言えないと感じました。
別データへの転用可能性は?
例えば大規模データで事前学習して別の小規模データでファインチューニングや転移学習をしたい、というシーンは多々あると思います。異なるデータセットに適用できると嬉しいですよね。
しかし本論文では、異なるデータセットでファインチューニングし精度を見るような実験は行われていないようです。実験中は一貫して、全体で1つのグラフである(グラフ数=1の)データセットを扱っています。
似たようなグラフだと分かっている他のグラフにも通用するパラメータは獲得できているのでしょうか?それとも最初に学習したグラフのノードについてしか通用しないのでしょうか?他のデータセットへの適用性がとても気になります。
Pubmedで事前学習したモデルをCoraでファインチューニングするとどうなるか、など知りたいところです(^^;)
GRAPH-BERTの本旨は何か
以上のような点が気になり、一般的なBERTのような、
- 大規模データで汎用モデルを事前学習し、少量データでファインチューニングする
- 事前学習で汎用的なEncoderの素を獲得することにより、各タスクでSOTAを達成する
といった趣旨のものではないのだなという感想を持ちました。“GRAPH-BERT”という論文名から勝手に期待しすぎてしまったのかもしれません。
せっかくならBERTのようにグラフデータの大規模事前学習済み汎用モデルが欲しいところですが、「自然言語」や「画像」のように人間の共通認識的な特徴量がグラフ自体には無いので(ノードがどのようなデータかに依存するわけで、グラフは構造でしかない)、難しいんだろうなと思います。
グラフデータをTransformer(BERT)で学習できるようにしてみたら、結構良い精度が出たよ!というのが本旨なんだと思いました。
※もしも「そうじゃないよー」「いやこう思うなぁ」など、私と違うような意見感想等ありましたらぜひ知りたいのでコメントくださると幸いです。
おまけ:公式実装コードを動かしてみる
4つのスクリプトが丁寧なことに用意されているのでそれを使用しましょう。
- script_1_preprocess.py:前処理用スクリプト
- script_2_pre_train.py:教師なし学習用スクリプト
- script_3_fine_tuning.py:教師あり学習用スクリプト
- script_4_evaluation_plots.py:script_2やscript_3で得られた実験結果(result)を可視化するためのスクリプト
公式リポジトリには、最も小規模なcoraデータセットとその関連コードのみが上がっています。
またscript_1で作成できる3種類のEmbeddingデータについても、coraデータセットに対応した分はリポジトリに上がっていますので、これをわざわざ動かさなくてもscript_2から実行できるようになっています。
python script_2_pre_train.py
またスクリプト内では、if 1:とif 0: によって実行するパート(タスクや手法など)を分別・管理しているので、学習に使用するデータセット名やハイパーパラメータと合わせて編集してから実行すると良いかと思います。
参考文献
-
BERT
-
GNN特有の問題(suspended animation problemやover-smoothing problem)についての参考論文