「大石泉すき」アドベントカレンダー 5日目を担当させていただきます。
はじめてのアドベントカレンダー参加です。気合が入ります。
今回はQRコードを既存のライブラリに頼ることなく、一から作成する手順を紹介していきます。既存のライブラリが充実している今では特に役立つというわけでもありませんが、QRコードってこんな感じに作られるんだなーという感じの読み物としてご覧ください。
本記事の内容について
データとして「大石泉すき」というテキストを格納したQRコードを作り、それを既存のQRコードリーダーで読み取らせるところまでを解説していきます。QRコードの仕様については必要な部分だけに絞って解説します。
参考にしたサイト
まず、この記事はオリジナルではなく、webで似たようなことをやっているサイトの情報を元に後追いでチャレンジしたものになります。
QRコードをつくってみる(http://www.swetake.com/qrcode/qr1.html)
本記事ではここを参考にしつつも詰まったところを重点的に解説していきます。
また、QRコードを実装する上では規格となるJISの情報は欠かせません。JISのサイトにて規格書を読むことができます(印刷は不可)。直接飛ぶURLが得られないので、「JISX0510」でデータベース検索してください。参照したバージョンは2018年に更新された「X0510 : 2018」です。
その他沢山のサイトで情報を得ましたので、本記事の最後で紹介します。
QRコードの種類を決める
一概にQRコードとは言っても、実はたくさんの種類があります。コンパクトでマス目の大きいものから、めちゃくちゃ大きくて目の細かいやつまで、実に40以上のバージョンがあります。
何が違うのかといえば、基本的には2点、容量と誤り訂正力の強さです。容量は5バイトから約3700バイトまで、誤り訂正は全体の7%~30%まで一部が読み取れずともリカバリしてくれます。
今回は「大石泉すき」というテキストを含むだけのシンプルなコードを作りたいので、小さいものを選択します。具体的にはバージョン2-Hと呼ばれる、一辺25マスのQRコードです。容量は16バイトになります(規格書P.31表7)。また、誤り訂正力は30%と最も高いものを選択しました。
漢字やひらがななら9文字入ります。「アナスタシアすき」はセーフ。「イヴ・サンタクロースすき」は残念ながら入りません。
このバージョンの場合の全体データ構成は以下のようになります。
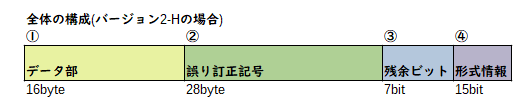
こんな形をしています。
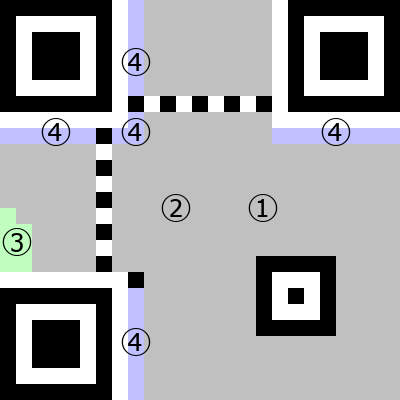
3つの隅にある大きな目玉みたいな模様が「位置検出パターン」(と隣接する白い「分離パターン」)。それらをつなぐ横断歩道みたいな模様が「タイミングパターン」、右下側にある小さな目玉が「位置合せパターン」です。これらは「機能パターン」と呼ばれ、常に色が決まっています。
一方、格納するデータによって変わるのが符号化領域です。以下3種類になります。
| 番号 | 容量 | 詳細 |
|---|---|---|
| ①データ部 | 128bit | 格納するデータの情報と、その種類を識別するための情報が含まれます |
| ②誤り訂正記号 | 224bit | ①,②の部分が一定数読み取り失敗しても正しくデータを読み取れるようにします |
| ④形式情報 | 15bit | 誤り訂正レベルやマスクの情報を格納します。また、この情報自身も一部欠けてもいいように②とは別の誤り訂正情報を含みます。 |
他のタイプのQRコードには他にも「型番情報」っていうのがあったりしますが、今回のには無いので割愛します。また、それ以外に以下の部分があります。
| 番号 | 容量 | 詳細 |
|---|---|---|
| ③残余ビット | 7bit | 図形の余り部分。ビット0で埋めます |
これらを作れればQRコード完成です。道のりは長いですが、お付き合いください。
QRに込めるデータを用意する
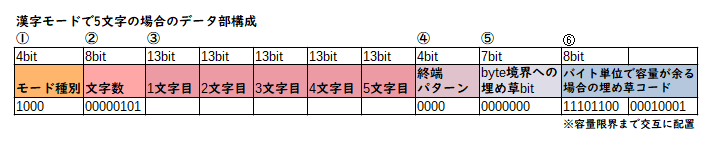
データ部の詳しい構成は以下の通りになります。
モード種別
QRコードでは容量が貴重なので、入れるデータ種別に特化したモードがいくつか用意されています。今回は漢字に特化した漢字モードを選択します。Shift-JISの文字コードに含まれる文字しか使えませんが、今回はこれで十分です。漢字モードを表す識別コードは1000(2進)です。なお別のモードを使えばUnicodeの文字列を使うことができます。
文字数
漢字モードの場合は8ビットで文字列の長さを格納します。別のモードでは9ビットだったり10ビットだったりと異なります。今回は5文字なので00000101ですね。
文字データ
対象となる文字の種類はShift-JISに依存しています(最近はUTF-8が随分普及したのであまり使わなくなりましたね……)。Shift-JISでは1文字を16ビットで表現しますが、全部で約7000文字強なので、13ビット(213=8096)で表すことができます。以下の手順でShift-JISの文字コードを専用の13ビットコードに変換します。
| 条件 | 変換手順 |
|---|---|
| 文字コードが0x8140~0x9FFC の範囲の場合 |
1. 0x8140を引く 2.上位バイトに0xC0を足す 3.上位バイトに下位バイトを加算 |
| 文字コードが0xE040~0xEBBF の範囲の場合 |
1. 0xC140を引く 2.上位バイトに0xC0を足す 3.上位バイトに下位バイトを加算 |
処理が2種類に分かれているのはShift-JIS自体が大きく2つの区画(厳密には4つ)に分かれているからですね。(参考) (または規格書P.89)
これにより、「大石泉すき」は以下のように変換されます。
| 文字 | Shift-JIS(16進) | 13ビットコード(2進) |
|---|---|---|
| 大 | 0x91E5 | 0110010100101 |
| 石 | 0x90CE | 0101111001110 |
| 泉 | 0x90F2 | 0101111110010 |
| す | 0x82B7 | 0000100110111 |
| き | 0x82AB | 0000100101011 |
終端パターン
ここがデータの終わりだよ、ということを示すための情報。4ビットで0000固定。ただし、残り容量が3ビット以下の場合は一部または全部を削ってはみ出さないようにします。
埋め草ビット
~~草生える。~~ここまでの処理で合計ビット数が8の倍数にならないとき、8の倍数になるまで埋め草ビット=ビット0で埋めます。今回はここまで4+8+13*5+4=81なので7ビットを埋めます。0000000
埋め草バイト
ここまでの処理で、まだ容量が余っている場合は、容量いっぱいまで11101100と00010001を交互に埋めていきます。
最終的に
今までの内容をまとめると
1000 00000101 0110010100101 0101111001110 0101111110010 0000100110111 0000100101011 0000 0000000 11101100 00010001 11101100 00010001 11101100
8ビット毎に整理すると
10000000 01010110 01010010 10101111 00111001 01111110 01000001 00110111 00001001 01011000 00000000 11101100 00010001 11101100 00010001 11101100
10進整数に変換して
128 86 82 175 57 126 65 55 9 88 0 236 17 236 17 236
できました。
誤り訂正符号を計算する(とてもつらい)
ここが最難関でした。QRコードではデータの一部(つまり黒か白か)が正しく読み取れなくてもデータが正しくデコードできるように、リード・ソロモン符号(以下RS符号)という方式で誤り訂正符号を付加します。この計算方法がもう数学苦手勢にはたいへんにつらいです。
非常に長い節となっておりますので、まずはここを飛ばして最後まで読んでみるのがいいかもしれません。
問題
いろいろと端折って言いますと、ここで解かなければいけない問題は以下のものです。
原始多項式x^8+x^4+x^3+x^2+1を用いた \\拡大ガロア体GF(2^8)において \\
N = 44, K = 16 \\
I(x) = d_1x^{15}+d_2x^{14}+d_3x^{13}+d_4x^{12}+d_5x^{11}+d_6x^{10}+d_7x^9+d_8x^8 + \\ d_9x^7+d_{10}x^6+d_{11}x^5+d_{12}x^4+d_{13}x^3+d_{14}x^2+d_{15}x+d_{16}
\\
G(x) =
x^{28}+α^{168}x^{27}+α^{223}x^{26}+α^{200}x^{25}+α^{104}x^{24}+α^{224}x^{23}+α^{234}x^{22}+α^{108}x^{21}+ \\
α^{180}x^{20}+α^{110}x^{19}+α^{190}x^{18}+α^{195}x^{17}+α^{147}x^{16}+α^{205}x^{15}+α^{27}x^{14}+ \\α^{232}x^{13}+
α^{201}x^{12}+α^{21}x^{11}+α^{43}x^{10}+α^{245}x^{9}+α^{87}x^{8}+α^{42}x^{7}+ \\
α^{195}x^{6}+α^{212}x^{5}+
α^{119}x^{4} +α^{242}x^{3}+α^{37}x^{2}+α^{9}x +α^{123}
\\としたとき \\
P(x) = x^{N-K} I(x) \quad mod \quad G(x)
\\
を求めよ
...
...
...
は? 意味わかんないですけど?
アホみたいな高次多項式を目のあたりにして、「むーりぃー」と叫びながら逃げ出したくなるわけですが、当然ながら、解けるように作られているのです。一つずつ説明しながら進めたいと思います。
GF2について
まず問題に着手する前に、GF(2)と呼ばれる数学の概念について説明が必要だと思います。私も覚えたてなのでろくに説明できませんが、簡単にいうと、「数字を0と1の二種類しか持たない、特殊な計算ルールを持つ世界」のことを指します。この世界では足し算と引き算のルールは以下のようになります。
足し算
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
引き算
| - | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
はい、足し算と引き算は全く同じ結果になります。またこの結果でわかる方が多いと思いますが、これはビットのXOR(排他的論理和)と合致しています。このあたり、計算機にとっても都合のいいところがあります。これをどんどん拡張することで、いろいろな応用ができるようになります。
ちなみにGFとはGalois Fieldの略で、日本語だとガロア体、あるいは有限体などと呼ばれます。
原始多項式とGF(28)について
原始多項式とは、GF(pm)を拡張して応用する際に使われる特別な多項式のことです。GF(2)を拡張する際にも用いられます(p=2,m=1)。
GF(28)とは、GF(2)を拡張した、これもまた特殊な計算ルールが存在する世界のことです。GF(2)では0と1の2個の数値しか含みませんでしたが、GF(28)では28=256個の数値を含みます。こちらは8ビットの演算に対してとても都合がいいのでよく使われるようです。
GF(2)をGF(28)に拡張する際に、原始多項式を使いますが、原始多項式にもいくつか種類があり、RS符号の計算を行う場合、どれを使うかで計算結果が変わってくるため、QRコード作成の際にはx8+x4+x3+x2+1を使うよ、と明確に指示されているわけですね。
αってなに?
関数G(x)に登場するαとは、原始多項式F(x)=x8+x4+x3+x2+1の根、すなわちF(x)=0としたときの解のことです。そしてGF(28)に含まれる256個の数値(専門用語で元ともいう)を構成するとても重要な存在です。αのもつ性質がこの問題を解くために必要になるため、長いですがじっくり解説していきます。
αはF(α)=0を満たすので、以下の式が成立します。
α^8+α^4+α^3+α^2+1 = 0 \tag{1}
このとき、各項の係数はすべてGF(2)の世界に属します。すなわち、0と1の2種類の値しかとらず、足し算と引き算の結果はどちらもXORに等しい、ということです。それを踏まえて(1)を変形します。
α^8 = α^4+α^3+α^2+1 \tag{2}
ちょっと「ん?」と思うかもしれませんが、移項した際にマイナスが付かないのは誤りではありません。足し算と引き算が同じなのですから、この世界では+/-の区別はないといって差し支えありません(α8=1α8=(0-1)α8=-α8)。
αの累乗を求める
αの累乗はとても大切な性質を持っています。そのことを語るために、まずはae(eは0以上の整数)をどんどん計算していきます。α8はα4+α3+α2+1に等しいので、α9,α10,α11は
α^9 = α^5 + α^4 + α^3 + α \\
α^{10} = α^6 + α^5 + α^4 + α^2 \\
α^{11} = α^7 + α^6 + α^5 + α^3 \\
となりますね。α12では
\begin{align}
α^{12} &= α^8 + α^7 + α^6 + α^4 \\
&= (a^4 + a^3 + a^2 + 1) + a^7 + a^6 + a^4 \\
&= a^7 + a^6 + (1+1)a^4 + a^3 + a^2 + 1 \\
&= a^7 + a^6 + a^3 + a^2 + 1
\end{align}
3行目ですが、αの係数では1+1=0が成立するので、α4の項は消滅します。もうわかっちゃうと思うのですが、α8が置き換えられるおかげで、αの次数がいくら高くなろうとも、たかだかα7以下の最大8項に置き換えることができます。
α^e = b_1α^7 + b_2α^6 + b_3α^5 + b_4α^4 + b_5α^3 + b_6α^2 + b_7α + b_8
b1~b8はGF(2)に属する数値(0か1)です。ビット演算感がでてきましたね。
そしてずっとαの次数を上げていくと、
α^{255} = 1
を得ることができます。α0 = 1ですので、αeは255個周期でループするようになっています。
長くなってしまいましたが、ここで一番大事なことを言います。
αeについてeが0~254である範囲において、係数b1~b8はそれぞれ一意に定まる
つまりeとb1~b8はそれぞれ1:1対応できるということです。以下の表のようになります。
| e | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 9 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| ... | ||||||||
| 217 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 218 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 219 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| ... | ||||||||
| 252 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 253 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 254 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
全部はながすぎるので一部のみ記載しました。ここやここ(リンク先表4)に掲載されています。
また、以下に表を生成するコードを付けておきます。見たい人だけ。
表の生成プログラム
# e 0, 1, 2, 3, 4, 5, 6, 7, 8
buffer = [1, 0, 0, 0, 0, 0, 0, 0, 0]
print('e b1 b2 b3 b4 b5 b6 b7 b8 d10')
for e in range(1, 255):
# バッファを右シフトする
buffer = [0] + buffer[0:8]
if buffer[8]:
buffer[8] = 0
# a^8が発生したのでa^4+a^3+a^2+a^0に置換する
added = [1, 0, 1, 1, 1]
for i in range(len(added)):
# GF(2)において桁同士の加算はXORに等しい(そして繰り上げもない)
buffer[i] = buffer[i] ^ added[i]
n = sum([buffer[i] * (2 ** i) for i in range(8)])
print(e, list(reversed(buffer[:8])), n)
なおMaximaならたった5行で書けます(GFを扱うライブラリがある)
load("gf")$
gf_set_data(2, x^8+x^4+x^3+x^2+1)$
binmap(n) := makelist(coeff(gf_exp(x, n), x^k), k, 7, 0, -1)$
exp2num(n) := lreduce(lambda([x,y],2*x+y), binmap(n))$
for n : 0 thru 254 do print(n, binmap(n), exp2num(n));
αeについて、同じ値をeあるいはb1~b8の2通りの表現で表せることが分かりましたので、本記事では以降、それぞれe表現、b表現と呼ぶことにします。この2つの表現の使い分けが鍵になります。
αの累乗どうしの演算について
αの累乗どうしの演算の法則について説明します。
まずは掛け算です。
二つの値αiとαjを掛ける場合、
α^iα^j = α^{i+j} \tag{3}
となります。これはまあ高校数学でも習う範囲なので問題ないと思います。後で使います。
次は足し算と引き算です。
α^i + α^j = ? \\
α^i - α^j = ?
この計算はe表現ではできません。でも、b表現ならできます。
α^i = b_{i1}α^7+b_{i2}α^6+b_{i3}α^5+b_{i4}α^4+b_{i5}α^3+b_{i6}α^2+b_{i7}α+b_{i8} \\
α^j = b_{j1}α^7+b_{j2}α^6+b_{j3}α^5+b_{j4}α^4+b_{j5}α^3+b_{j6}α^2+b_{j7}α+b_{j8} \\
とおくと \\
\begin{align}
α^i + α^j = α^i - α^j &= (b_{i1} \oplus b_{j1})α^7 + (b_{i2} \oplus b_{j2})α^6 + (b_{i3} \oplus b_{j3})α^5 \\
&+ (b_{i4} \oplus b_{j4})α^4 + (b_{i5} \oplus b_{j5})α^3 + (b_{i6} \oplus b_{j6})α^2 \tag{4} \\ &+ (b_{i7} \oplus b_{j7})α + (b_{i8} \oplus b_{j8})
\end{align}
〇の中に+はXOR(排他的論理和)を表す記号です。
これはすなわち、e表現での足し算,引き算はb表現での係数毎のXORに等しいことを表しています。もっと簡単に言えば表における8ビットどうしのXORに等しいです。
(3)式と(4)式により必要な道具はそろいました。
dってなに?
次に関数I(x)に出てくる係数dについて説明します。
もう一回I(x)を書いておきますね。
I(x) = d_1x^{15}+d_2x^{14}+d_3x^{13}+d_4x^{12}+d_5x^{11}+d_6x^{10}+d_7x^9+d_8x^8 + \\ d_9x^7+d_{10}x^6+d_{11}x^5+d_{12}x^4+d_{13}x^3+d_{14}x^2+d_{15}x+d_{16}
d1~d16はRS符号によって保護したいデータ、すなわち先だって求めた16バイト分のデータを含んでいる、それぞれが1つにつき8ビット分の情報を持つ変数αの高次式です。定義を書くと以下のようになります。
d = b_1α^7 + b_2α^6 + b_3α^5 + b_4α^4 + b_5α^3 + b_6α^2 + b_7α^1 + b_8
はい、αeに対応するb表現と同じものです。よって、入力データは8ビット毎にそれぞれd=αeの形に変換することができます。ちょっとやってみましょう。
データの最初の4バイト分は10000000 01010110 01010010 10101111でしたね。これを対応表を見ながら変換してみる(右側から左側のeの値を求める)と、
d_1 = α^7 \\
d_2 = α^{219} \\
d_3 = α^{148} \\
d_4 = α^{97}
(すみませんがd3,d4は表を省略した都合上載ってません)
同様にすべてのデータを変換してしまいます。ただ1点だけ注意が必要です。データが00000000の場合だけはαe=0となるeは存在しないので、これについてはαeの形で表すのは諦めて項自体を削ってしまうことにします。
結果としてI(x)は以下のようになります。
I(x) = α^{7}x^{15}+α^{219}x^{14}+α^{148}x^{13}+α^{97}x^{12}+α^{154}x^{11}+α^{167}x^{10}+α^{191}x^9+α^{185}x^8 + \\ α^{223}x^7+α^{241}x^6+0x^5+α^{122}x^4+α^{100}x^3+α^{122}x^2+α^{100}x+α^{122}
d11に対応するデータが00000000だったので、x5の項が消えました。
剰余P(x)を求める
ここで求めたい関数P(x)を思い出します。
\begin{align}
P(x) &= x^{N-K} I(x) \quad mod \quad G(x) \\
&= x^{28} I(x) \quad mod \quad G(x)
\end{align}
なのでx28I(x)を別の関数で置きなおします。
M(x) = x^{28}I(x) \\
= α^{7}x^{43}+α^{219}x^{42}+α^{148}x^{41}+α^{97}x^{40}+α^{154}x^{39}+α^{167}x^{38}+α^{191}x^{37}+α^{185}x^{36} + \\ α^{223}x^{35}+α^{241}x^{34}+0x^{33}+α^{122}x^{32}+α^{100}x^{31}+α^{122}x^{30}+α^{100}x^{29}+α^{122}x^{28}
そんでもってG(x)を改めて書きますと、
G(x) =
α^{0}x^{28}+α^{168}x^{27}+α^{223}x^{26}+α^{200}x^{25}+α^{104}x^{24}+α^{224}x^{23}+α^{234}x^{22}+α^{108}x^{21}+ \\
α^{180}x^{20}+α^{110}x^{19}+α^{190}x^{18}+α^{195}x^{17}+α^{147}x^{16}+α^{205}x^{15}+α^{27}x^{14}+ \\α^{232}x^{13}+
α^{201}x^{12}+α^{21}x^{11}+α^{43}x^{10}+α^{245}x^{9}+α^{87}x^{8}+α^{42}x^{7}+ \\
α^{195}x^{6}+α^{212}x^{5}+
α^{119}x^{4} +α^{242}x^{3}+α^{37}x^{2}+α^{9}x +α^{123}
まだまだ圧が強いですが、大分すっきりしました。
ところで多項式に対する剰余の求め方はどうやるのでしょうか。高校生の時に数Ⅱ-Bあたりでやったような気もします。思い出しがてら関数m(x) = x2+3x+1 を g(x)=x-1 で割った余りを求めてみます。
まず割られる側の式を置きますよね。
x^2 + 3x + 1
そんで割る側の式の次数と係数を割られる側に合わせますよね。
\begin{align}
& x^2 + 3x + 1 \\
-)& x^2 - x \hspace{2pc} ←xg(x)
\end{align}
そして引き算しますよね。最高次数の項を消します。
4x + 1
で、また同じように、
\begin{align}
& 4x + 1 \\
-)& 4x - 4 \hspace{2pc} ←4g(x)
\end{align}
残ったものが割る側の次数を下回ったのでここで終わります。したがって、余りは5となります。g(x)の最大次数の係数が1のときはこんな風にやりやすいんですよね。
P(x)も全く同じ方法で得ることができます。それでは実際にM(x)をG(x)で割るところを最初だけやってみます(すみませんが流石に全部は長大すぎて書ききれません)。
まずは互いの最大次数の項を確認します。M(x)はα7x43、G(x)はα0x28ですね。よって同じ値に合わせるためにG(x)にα7x15を掛けます。
\begin{align}
& α^{7}x^{43}+α^{219}x^{42}+α^{148}x^{41}+... \\
& α^{7}α^{0}x^{43}+α^{7}α^{168}x^{42}+α^{7}α^{223}x^{41}+... \hspace{2pc} ←α^7x^{15}G(x)
\end{align}
ここで式(3)を使用します。αの累乗どうしの掛け算は指数の足し算ですので、整理すると
\begin{align}
& α^{7}x^{43}+α^{219}x^{42}+α^{148}x^{41}+... \\
-)& α^{7}x^{43}+α^{175}x^{42}+α^{230}x^{41}+... \hspace{2pc} ←α^7x^{15}G(x)
\end{align}
この引き算の際に式(4)を使用します。累乗どうしの引き算は8ビットのXORを取るのでしたね。α219 - α175についてはα(01010110 xor 11111111) = α10101001 = α135ですね。α148 - α230 = α01010010 xor 11110100 = α10100110 = α207 ...。e表現(指数値)からb表現(2進数)へ変換する際、およびb表現からe表現に変換する際はかならず表を参照してくださいね(そのまま10進数<->2進数変換してはダメー)
あとはもう、どんどん最高次数の項を消す作業を繰り返すだけです。注意点としては、(3)式を使った後、指数が255以上になった場合はα255=1を利用して指数が255未満になるように修正してください。
最終的に割られる側がx28を下回った時点で終了し、R(x)は以下のように求まります。
R(x) = α^{248}x^{27}+α^{159}x^{26}+α^{237}x^{25}+α^{105}x^{24}+α^{12}x^{23}+α^{215}x^{22} \\
+α^{172}x^{21}+α^{102}x^{20}+α^{113}x^{19}+α^{149}x^{18}+α^{233}x^{17}+α^{135}x^{16}\\
+α^{51}x^{15}+α^{42}x^{14}+α^{233}x^{13}+α^{7}x^{12}+α^{44}x^{11}+α^{236}x^{10}+α^{216}x^{9} \\
+α^{159}x^{8}+α^{64}x^{7}+α^{70}x^{6}+α^{11}x^{5}+α^{0}x^{4}+α^{51}x^{3}+α^{5}x^{2}+a^{60}x^{1}+a^{168}
欲しかったもの(RS符号)は、このR(x)の各係数部分の指数値です。よって
248 159 237 105 12 215 172 102 113 149 233 135 51 42 233 7 44 236 216 159 64 70 11 0 51 5 60 168
できました。しんどかった。
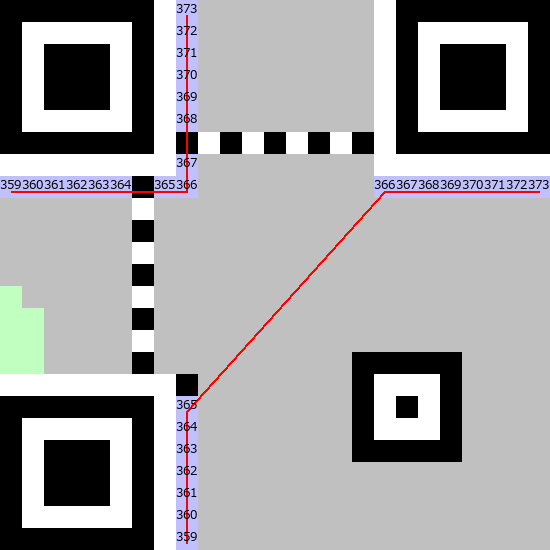
データと誤り訂正符号をマスに配置する
ここまでで、大体60~70%といったところです。あともうちょっとです。
なんとか作成したデータと誤り訂正記号を、画像の番号の通りに1ビットずつ配置していきます。データ16バイト・誤り訂正記号28バイトなので44*8=352ビットです。図の351のところまで埋めます。
残りの部分も色(0 or 1)を入れていきます
白い部分は明モジュールといって、ビット0を入れます。
黒い部分は暗モジュールといって、ビット1を入れます。
緑色の部分は残余ビットといって、端数の部分なのでビット0を入れます。
紫色の部分は最後に記入するのですが、現時点でどういう値を入れておくのがいいのかわからなかったので、仮に値TBDを入れておきます。詳しい方どうか教えてください。(規格書(P.45)には「一時的に空にしなければならない」と書いてありますが、空ってなんなんだ……)
図の紫部分だけ仮置きですが、一通り図形が出来上がりました。
適切なマスクを選ぶ(つらい)
QRコードにはデータの内容によって非常に読み取りづらいパターンが生成されるのを防ぐために、「マスク」という機能があります。それぞれ異なる8通りのパターンを使って、配置された白黒のパターンを部分的に反転させ、一番読み取りやすそうなパターンを最終的に生成するためのものです。
なので、QRコードを作るソフトウェア(エンコーダ)では、8通りのマスクを全て試してみて、一番良いものを選択しなければなりません。
マスク種別
マスクの種類は以下の8種類です。(算出式は省略。詳細は規格書P.49)

マスク対象に含む部分
- データ部分
- 誤り訂正符号
マスク対象に含まない部分(上に挙げたもの以外)
- 機能パターン(位置検出,タイミング,位置合せ)
- 形式情報
- 残余ビット
評価
それぞれのマスクを適用した後、4種類の評価基準によって、点数評価を行います。評価は減点方式で、失点が一番少ないものを実際に使用することになります。
評価対象はQRコード全体となります。
(ただ、まだ色が決まっていない部分があるのでそれをどうするのかが不透明……)
評価基準は以下のとおりです(規格書P.53表11)。
| 評価番号 | 評価内容(ざっくり) | 減点方法(ざっくり) |
|---|---|---|
| 1 | 横あるいは縦に5個以上連続する同色のマスがある場合減点 減点は一番長い連続数で1回だけ評価 (同じマスに対して2度減点しない) |
5連続で-3 6連続で-4 7連続で-5 ... |
| 2 | 2x2サイズの同色ブロック(明・暗両方)がある場合減点 一部重複していても全部カウントする |
1つにつき-3 ※1 |
| 3 | 暗:明:暗:明:暗=1:1:3:1:1のパターン(※2)に隣接する4連続の明モジュールがある場合減点 | 1つにつき-40 |
| 4 | 暗モジュールの割合が偏っている場合は減点 | 50%から誤差5%以内は減点なし。誤差5%増える毎に-10 |
ここの説明はとてもざっくり書いたので、正確な内容については規格書のほうを参照してください。
※1 3隅にある位置検出パターンの内側にある黒い3x3の暗モジュールパターンについても必ず減点(計-36点)します。しますが、この部分にはマスクが掛からないので、8つ全てのマスクの評価で等しく減点されるため、マスクの選択結果に影響はありません。
※2 3隅にある大きな位置検出パターンのことを指しています。
実際に評価してみたところ、減点が発生したのは評価1と評価2だけで、評価3と4については8つのマスク全てにおいて減点なしでした。**評価3については形式情報の部分に値TBDとかいう値を入れてしまったせいで、まったく評価が機能しなくなってしまいましたが、これはどうなんでしょうね……**やっぱり明モジュールを入れとくのが妥当なのか……?
今回最少失点で選択されたのはマスクパターン111(上の画像の右下)でした。
そして選択されたマスクを実際に適用します。
形式情報を計算する
最後に残った部分を埋めます。残ったのは「形式情報」と言われる部分です。
形式情報に含まれるのは以下の2つです。
- 誤り訂正レベル(2bit)
10 - 選択したマスクパターン番号(3bit)
111
誤り訂正レベルは今回は'H'を選択したので10です。他のレベルについては規格書(P.54表12)を参照してください。
この5ビットの情報10111をもとに、BCH符号を算出します。これもRS符号と同じような誤り訂正符号の一種です。「また数学かー」と思われるかもしれませんが、同じような処理の流れで、しかもこっちは大分簡単なので大丈夫です。
BCH符号
こちらの場合も関数I(x)とG(x)が定義されており、以下のような問題を解きます。
N = 15, K=5 \\
I(x) = 1x^4 + 0x^3 + 1x^2 + 1x + 1 \\
G(x) = x^{10} + x^8 + x^5 + x^4 + x^2 + x + 1 \\
において \\
P(x) = x^{N-K}I(x) \quad mod \quad G(X) \\
を求めよ
I(x)の各係数は誤り訂正レベルとマスク番号のビットを並べたものです。
今回はとてもありがたいことに、全ての係数が0か1なので、非常に計算がしやすいです。
結果だけ書くと0000101001が得られます。
これを既にある5bitの後ろに連結し、規定のマスク101010000010010とのXORを取って完成です。
\begin{array}{c}
\begin{align}
& 101110000101001 \\
\oplus & 101010000010010 \\
\hline
& 000100000111011
\end{align}
\end{array}
規格書のP.76表C.1には正解の値が載っていますが、ちゃんと一致しています。よかった。
形式情報をマスに配置する
最後に今求めた形式情報の15ビットを、未だ空いている部分に書き込みます。
同じものを2か所別の場所に書き込む必要があります。
QRコード画像を作る
最後に画像にして完了です。等倍で画像を作って補間なしで拡大するのが一番楽っぽい。
周囲に最低4マス分のクワイエットゾーン(白い余白)を付け加えるのを忘れずに。
完成!!なかなかの道のりでした!
動作確認
さて、作ったものはちゃんと読み取れるでしょうか。
できてるー。
iPad、Androidタブレット、Windows用のフリーソフトで試してみましたが、いずれも問題なく読み取れました。こんなにすんなり行くとは思ってませんでした。
ちなみに、最初形式情報にマスクをかけるのを忘れてそのまま出力したんですが、それでもちゃんと読み取ってくれてました。デコーダ側が頑張ってなんとかしてくれているのでしょうか。
感想
実際にQRコードを作る過程を体験することにより、かつて読んで首を傾げた記事「QRコードを人力で読み取る」も「あー、なんとなくできそう」という気持ちになることができました。
本記事を読んでQRコードって意外と簡単に作れるんだ、と思っていただけたら幸いです。
今回作成したソースコード(言語はPython)はちょっと長くなってしまったので外部のサイト(Github)においてあります。煮るなり焼くなりどうぞ。(QRコードを名刺にでも貼るといいんじゃないかな、P的に)
「大石泉すき」と表示するQRコードの生成プログラム
参考リンク
参考にさせてもらったサイトや、本記事に関連して読んでみるのを推奨するリンクを貼っておきます。
QRコード全般
QRコードをつくってみる
: 今回一番参考にさせていただいたサイト
QRコードドットコム
: QRコードを開発したデンソーのサイト。QRコードについておおまかに理解できる
QRコード Deep Dive ーデータ符号化とか誤り訂正とかー
: 本記事をほぼ書き終わったところでみつけたページ(灯台元暗し)。執筆前にQiita内の記事は探したはずなのになぜ見逃したのか、これがわからない。
Creating a QR Code step by step
: (英語)QRコードの作成の過程を1ステップごとに詳細な情報と共に図示してくれるすごいサイト。
RS符号関連
ガロア体と拡大体
: ガロア体について分かりやすい記事1
ガロア体講座
: ガロア体について分かりやすい記事2
ウィキペディア - リード・ソロモン符号
: 説明例で使っている式がQRコードで使うものと同じなので大変参考になります
Reed–Solomon codes for coders
: 英語ですが、全般的に説明されているので読める方は是非
その他
CRC-32
: CRC-32についての説明スライドです。データ破損チェックによく使われるCRCもまたガロア体を利用した技術です。合わせて読むと理解が深まります、多分。
大石泉 (おおいしいずみ)とは【ピクシブ百科事典】
: 大石泉って誰だよ、という方に