本記事はFusic Advent Calendar 2018の18日目の記事です。
昨日は@kawano-fusicがOJTで作った社内の振返り会システムを全力で振り返っていました。振返りは大事ですね。
最近の世の中はQRコードで溢れています。
Webサイト行くにもQRコード、飛行機乗るにもQRコード、友達になるにもQRコード、電子決済するにもQRコード、猫も杓子もQRコード、QRコード…。
Fusic Advent Calendar 2018 16日目で@gorogoroyasuが触れていましたが、先日リリースされたOpenCV4.0でもQRコードまわりの強化がなされているようです。
ですが、このQRコードの仕組みを知っている人はあまりいません。
単にマーカーと生のビット列を並べてあるだけなんて思ってやしませんか?
もしそう思っていたならば、この脳みそがとろけそうな複雑さに驚愕するでしょう。
今回は、QRコードにDeepにDiveして、データ符号化や誤り訂正について解説してみようと思います!
実務的にはあんまり役には立たないかもしれませんが、単に技術的な読み物として純粋にQRコードを楽しんで、QRコードスゲェ!となってくれれば幸いです。
面白いですよ、QRコード。
QRコードの特徴
まずは手始めに、QRコードはどんな特徴を持っているのかを見ていきましょう。
高速で安定した読み取り性能
QR = Quick Response の略なだけあって、高速に読み取ってくれます。
(今のコンピューターの性能だと多少効率悪くても人間には高速に感じそうですが、誕生したのが1994年なので…)
また、回転したり歪んだりしても安定して読み取れるようにもなっています。
存在感のある位置検出パターン/位置合わせパターンはもちろんですが、大きくあと2つあります。
- 目立つ3つの隅のシンボルもあるし、よーく見ると白黒が交互に現れるラインが…
- 白ばっかり、黒ばっかりのQRコードって見たことなくないですか?
詳しくはまた後ほど。
大量のデータ格納
安定した読み取り性能を持つため、かなり大きなQRコードの作成も可能です(最大で177x177)。
また、格納する文字の種類によって効率的にデータを収められるようになっているため、
英数字(+一部の主要な記号)であれば、最大の177x177のQRコードで4,296文字が格納できます。
177x177 = 31,329[bit] ≒ 3,916[byte] < 4,296[文字]
このデータ符号化手法についても後ほど解説します。
汚れ・破損に強い
QRコードには、「リード・ソロモン符号」を使った誤り訂正方式を採用しています。
QRコードに限らず、地デジやCD, DVDなんかにも使われている一般的なものです。
仕様として誤り訂正のレベルは4段階用意されていますが、最大30%欠損しても読み取れてしまいます。
この誤り訂正の内容についてもできる限り解説してみます。
実は日本製
これはちょっと有名かもしれませんが、QRコードはデンソー(現在は分離しデンソーウェーブ)が開発したものです。
そのため、かなや漢字(Shift_JIS)が格納できる仕様があったりします。
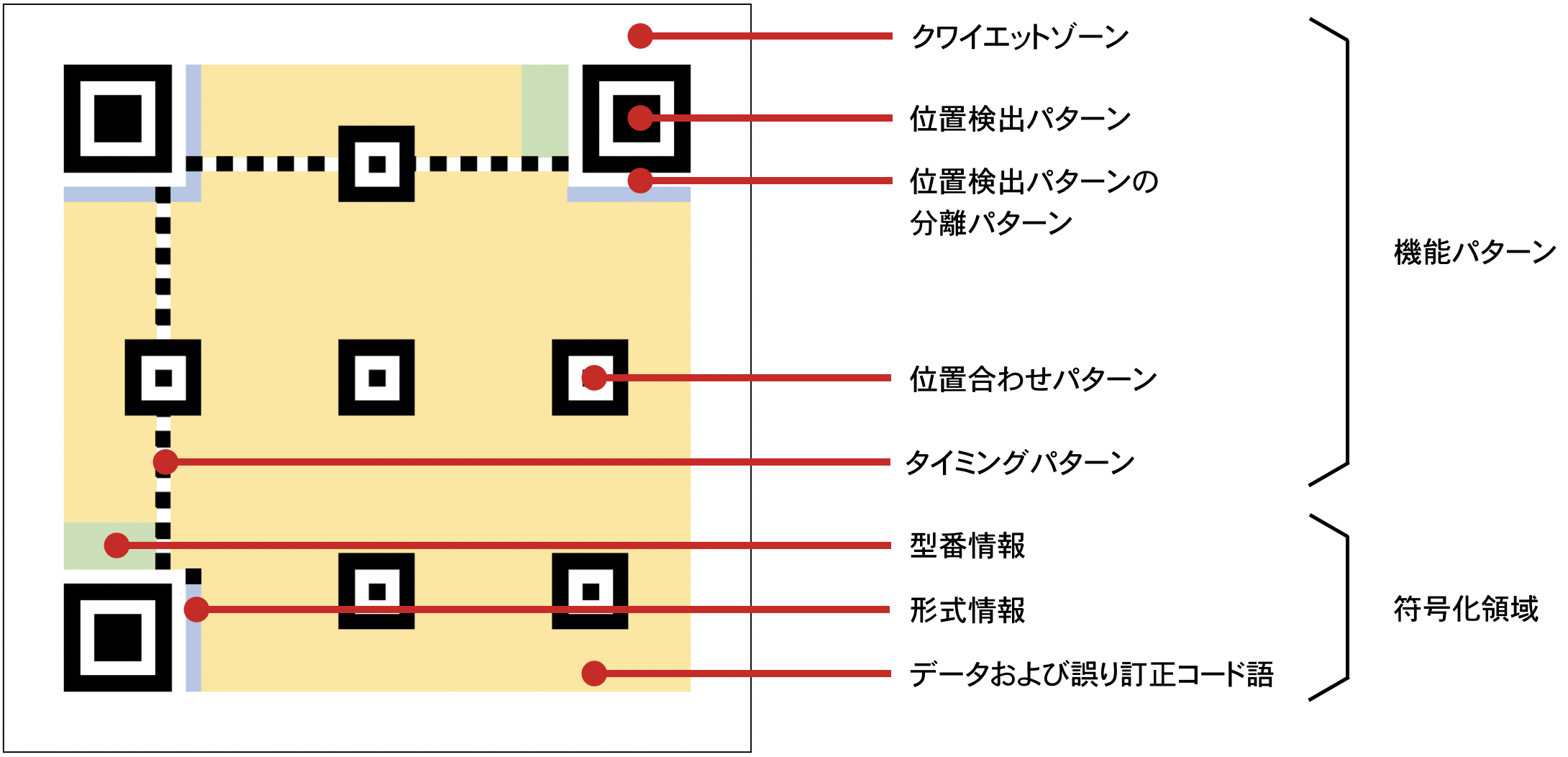
QRコードの構造
機能パターン
画像からの読み取りを行いやすくするためにある領域です。
クワイエットゾーン
シンボルを囲むセル4つ分の空白領域です。
周囲のノイズからシンボルを切り離すことで読み取るべき領域を明確にします。
位置検出パターン
シンボルの3つの隅に配置された7x7のパターンです。
1つの隅にこのパターンが無いので、シンボルの位置と同時に向きも分かってしまいます。
360度どの方向からスキャンしても、このパターンの中心を通る場合は必ず黒白黒白黒の比率が1:1:3:1:1になります。
画像から読み取る際は、これを目印に位置検出パターンを認識します。
また、位置検出パターンの周囲にある分離パターンも、検出のしやすさに地味に貢献しています。
位置合わせパターン
大きなシンボルになると出現する、5x5のパターンです。
斜め上から読み取られてシンボルが台形になったり、ちょっと歪んだりしていた場合に変形を補正するために使われます。
タイミングパターン
言われないと気づかない、白黒が交互に現れるライン。
こちらも同様に変形の補正用です。
符号化領域
データを持っている領域です。
型番情報
QRコードのバージョンの情報を持っている領域です。
バージョンといっても、ここではシンボルの大きさを表します。
21x21のバージョン1から、4セル刻みで177x177のバージョン40まで存在します。
ただし、型番情報を持っているのはバージョン7からです。
7未満は小さいので、型番情報がなくてもセルの数を数えるやり方で十分ということではないかと。
ちなみに、2箇所に存在していますが同じ値が入っています。
汚れなどで片方が読めなくなっても大丈夫なように冗長化しています。
形式情報
誤り訂正レベルとマスク識別子の情報を持っている領域です。
誤り訂正レベルは訂正できるエラーの数を決めます。レベルは4段階用意されています。
マスク識別子はデータ格納時に適用するマスクパターンの種類を表します。このマスクによって読み取り性能を向上させます。
詳細は後ほど。
こちらも冗長化されており、左上の位置検出パターンの周囲の領域と、他の2か所を合わせたものには同じ値が入ります。
データおよび誤り訂正コード語
QRコードの仕様に沿って符号化されたデータとそれに対する誤り訂正コードが入っています。
以降は、このデータの符号化手法と誤り訂正方式について解説していきます。
データ符号化
さて、ようやく本題です。
QRコードは、情報を詰め込むために独自の手法でデータを符号化しています。
符号化データは、次の要素を順に並べたものです。
- モード指示子
- 文字数指示子
- データコード語
- 終端パターン
- 埋め草ビット
- 埋め草コード語
- 誤り訂正コード語
ここでは、それぞれの要素を順に解説していきます。
モード指示子
QRコードでは、少しでも多くのデータを格納するため、扱う文字種によって詰め込み方を変えます。
これを符号化モードと呼び、以下の4種類が用意されています。
そして、この符号化モードを表す4ビットのデータがモード指示子です。
| 符号化モード | モード指示子 | 扱えるコード | 必要なビット数 | 補足 |
|---|---|---|---|---|
| 数字モード | 0001 | 0-9 | 10ビット/3文字 | |
| 英数字モード | 0010 | 0-9, A-Z, 空白, $, %, *, +, -, ., /, :
|
11ビット/2文字 | 小文字のアルファベットは扱えない。 |
| 8ビットモード | 0100 | すべての文字 | - | バイナリがそのまま入れられるのでオールマイティ。 |
| 漢字モード | 1000 | JIS X 0208で規定される漢字集合 | 13ビット/1文字 | 漢字、2バイトのひらがな・カタカナ・英数字など。半角文字は扱えない。 |
文字数指定子
その名の通り、格納される文字数を指定するものです。
バージョンと符号化モードによって格納できる文字の最大数が決まるため、それに合わせて文字数指示子に使われるビット数が変わります。
1ビット単位で節約してやろうという気合が表れていますね!
| バージョン | 数字モード | 英数字モード | 8ビットモード | 漢字モード |
|---|---|---|---|---|
| 1-9 | 10 | 9 | 8 | 8 |
| 10-26 | 12 | 11 | 16 | 10 |
| 27-40 | 14 | 13 | 16 | 12 |
データコード語
符号化モードごとに符号化の手法が異なります。
数字モード
データを3文字ずつに区切り、それぞれを3桁の数字とみなして10ビットで表します。
余りが出たら、1桁なら4ビット、2桁なら7ビットで表します。
例)
12345
-> 123 45
-> 0001111011 0101101
英数字モード
このモードでは、各文字に数値が割り当てられています。
| 文字 | 対応する値 |
|---|---|
| 0-9 | 0-9 |
| A-Z | 10-35 |
| 空白 | 36 |
| $ | 37 |
| % | 38 |
| * | 39 |
| + | 40 |
| - | 41 |
| . | 42 |
| / | 43 |
| : | 44 |
そして、データを2文字ずつに区切り、それぞれを45進数的に解釈して11ビットで表します。
つまり、1文字目の値に45を掛け、2文字目の値を加えます。
余りが出たら、対応する値を6ビットの値にします。
例)
A/B
-> A/ B
-> 10x45+43 11
-> 00111101101 001011
8ビットモード
バイナリそのままです。
漢字モード
各文字のShift_JIS表現を以下のように変換します。
- 上位バイトが0x81-0x9fなら0x81を、0xe0-0xebなら0xc1を引き、結果に0xc0を掛ける
- 下位バイトから0x40を引き、1.に加える
- 結果を13ビットで表す
例)
あい
-> 0x82a0 0x82a2
-> (0x01 x 0xc0 + 0x60) (0x01 x 0xc0 + 0x62)
-> 0x120 0x122
-> 0000100100000 000010010010
(補足)符号化モードの混在
途中で符号化モードを切り替えることも可能です。
その場合、モード指示子 -> 文字数指示子 -> データコード語を繰り返していくことになります。
ただ、むやみに符号化モードを切り替えるとモード指示子と文字列指示子のオーバーヘッドによって却ってサイズが大きくなる可能性があるので注意が必要です。
そのあたりを完全に最適化しようと思うと…ものすごくめんどくさいコードが見えます。
終端パターン
データコード語のあとに付け加えて終端を示すパターンです。具体的には0000の4ビット。
データ容量の残りが4ビット未満であれば、溢れた部分は省略可能です。
埋め草ビット
QRコードでは8ビット(バイト)単位でデータを格納していくので、きれいに8ビットごとに区切れるようにする必要があります。
そのため、終端パターンまでのデータサイズが8で割り切れるように、埋め草ビットとして0を追加します。
埋め草コード語
QRコードが格納可能なバイト数はバージョンと誤り訂正レベルによって決まります。
埋め草ビットまでのデータのバイト数が格納可能なバイト数に満たない場合は、埋め草コード語と呼ばれるビット列で埋めていきます。
具体的には、11101100と00010001を交互に追加していきます。
誤り訂正コード語
埋め草コード語までのデータに対する、誤り訂正のためのデータです。
詳細は後述。
誤り訂正符号
誤り訂正の概要
QRコードには、「リード・ソロモン符号」と呼ばれる誤り訂正符号が採用されています。
全体的なイメージを持ってもらうために、ひとまず概要だけ説明します。
端的に一つの式で表すと、次のようになります。
\boldsymbol{m^{\mathrm{T}}}\times \boldsymbol{G}\times \boldsymbol{H} = \boldsymbol{O}
- $\boldsymbol{m}$ : QRコードに持たせたいメッセージ(モード指示子 - 埋め草コード語)のベクトル(1バイト/要素)。$\mathrm{T}$はあまり気にしなくて大丈夫です。計算できるように転置しているだけなので。
- $\boldsymbol{G}$ : 生成行列
- $\boldsymbol{H}$ : 検査行列
データを格納するとき
$\boldsymbol{m^{\mathrm{T}}}$に生成行列$\boldsymbol{G}$を掛け合わせると、$\boldsymbol{m}$は誤り訂正機能付符号に変換されます。
$\boldsymbol{m}$対応する誤り訂正符号を生成してくっつけるイメージです。
今後の説明のために、以下のように$\boldsymbol{x}$を定義しておきます。
\boldsymbol{x^{\mathrm{T}}} = \boldsymbol{m^{\mathrm{T}}}\times \boldsymbol{G}
QRコードには、この$\boldsymbol{x}$が格納されています。
データを読み取るとき
読み取ったデータを以下のように定義します。
\boldsymbol{y} = \boldsymbol{x} + \boldsymbol{e}
$\boldsymbol{e}$は各要素のエラーをベクトルにしたものです。
誤りなく読み取れれば$\boldsymbol{e} = 0$なので$\boldsymbol{y} = \boldsymbol{x}$となり、
\boldsymbol{y^{\mathrm{T}}}\times \boldsymbol{H} = 0
そうでなければ、
\boldsymbol{y^{\mathrm{T}}} \times \boldsymbol{H} \neq 0
となります(設定した誤り訂正能力の範囲内では)。
さらに、エラーが検出された場合、頑張って計算すればエラーの数や位置、内容まで特定することができます。謎の技術ですね。
検査行列
一旦、$\boldsymbol{x}$は天から授かったものとして置いておいて、
先に検査行列を使ってどのように誤り訂正を行うのかを見ていきましょう。
リード・ソロモン符号では、誤り行列は以下の$n\times2t$行列として定義されます。
$n$は$\boldsymbol{x}$の長さ、$2t$は誤り訂正符号の長さ(つまり$n-2t$が本来のデータの長さ)になります。
また、説明は長くなるので省略しますが、$t$は訂正可能なエラーの数になります。
$\alpha$は今のところは深く考えなくて大丈夫です。便宜的に置いている未知数で、エラー情報を求める過程で消えてなくなります。
値が何にせよ$\alpha^{0} = 1$なので、法則性が見えてきますね。
\begin{eqnarray}
\boldsymbol{H} = \left(
\begin{array}{ccccc}
1 & 1 & \ldots & 1 & 1 \\
1 & \alpha & \ldots & \alpha^{ 2t-2 } & \alpha^{ 2t-1 } \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
1 & \alpha^{n-2} & \ldots & \alpha^{ (n−2)(2t−2) } & \alpha^{ (n−2)(2t−1) } \\
1 & \alpha^{n-1} & \ldots & \alpha^{ (n−1)(2t−2) } & \alpha^{ (n−1)(2t−1) }
\end{array}
\right)
\end{eqnarray}
QRコードからデータを読み取るときを考えます。
読み取ったデータ$\boldsymbol{y}$に検査行列$\boldsymbol{H}$を掛けて求めたベクトルを$\boldsymbol{s}$と定義すると、
以下の式が成り立ちます。
\begin{align}
\boldsymbol{s^{\mathrm{T}}} &= \boldsymbol{y^{\mathrm{T}}} \times \boldsymbol{H} \\
&= (\boldsymbol{x^{\mathrm{T}}} + \boldsymbol{e^{\mathrm{T}}}) \times \boldsymbol{H} \\
&= \boldsymbol{x^{\mathrm{T}}} \times \boldsymbol{H} + \boldsymbol{e^{\mathrm{T}}} \times \boldsymbol{H} \\
&= 0 + \boldsymbol{e^{\mathrm{T}}} \times \boldsymbol{H} \\
&= \boldsymbol{e^{\mathrm{T}}} \times \boldsymbol{H}
\end{align}
$\boldsymbol{s}$と$\boldsymbol{H}$の値は分かっているので、そこから$\boldsymbol{e}$を求める問題になります。
$\boldsymbol{e}$が分かれば、$\boldsymbol{x} = \boldsymbol{y} - \boldsymbol{e}$から正しいデータ$\boldsymbol{x}$ が分かるのでめでたしめでたしです。
ただし、残念ながら単純には求められません。
$\boldsymbol{e}$は$n$次のベクトル、$\boldsymbol{H}$は$n\times2t$行列です。
つまりは未知数が$n$個、方程式が$2t$個の連立方程式と同等なわけですが、$n - 2t$が本来のデータの長さを表すので、$n > 2t$。未知数が多すぎます(ちなみに$\boldsymbol{H}$のランクは$2t$です)。
どうやって求めるのかというと…先ほど、さらっと「$t$は訂正可能なエラーの数になる」と書きました。
つまり、未知数は$n$個あるものの、本当に求める必要のある未知数は最大でも$t$個で、それ以外は$0$です(それ以上のエラーがあるときは訂正不可能なので諦める)。
そのためにはまず、エラーがいくつあるのか、エラーがどこにあるのかを特定しなければなりません。
それができれば、あとは普通に解けるはずです。
エラーの数を特定する
エラーの数を$j$個とし、$\boldsymbol{e}$の$p_0, p_1, \ldots, p_{j-1}$番目にエラーがあるとします。
$\boldsymbol{e}$の$p_0, p_1, \ldots, p_{j-1}$番目以外は$0$なので、$\boldsymbol{s^{\mathrm{T}}} = \boldsymbol{e^{\mathrm{T}}} \times \boldsymbol{H}$を展開すると次のようになります。
\begin{eqnarray}
\left\{
\begin{array}{l}
s_0 &=& e_{ p_0 } &+& e_{ p_1 } &+& \cdots &+& e_{p_{j-2}} &+& e_{p_{j-1}}\\
s_1 &=& e_{ p_0 }\alpha^{ p_0 } &+& e_{ p_1 }\alpha^{ p_1 } &+& \cdots &+& e_{p_{j-2}}\alpha^{p_{j-2}} &+& e_{p_{j-1}}\alpha^{p_{j-1}}\\
\vdots\\
s_{(2t-2)} &=& e_{ p_0 }\alpha^{ (2t-2)p_0 } &+& e_{ p_1 }\alpha^{(2t-2)p_1} &+& \cdots &+& e_{p_{j-2}}\alpha^{(2t-2)p_{j-2}} &+& e_{p_{j-1}}\alpha^{(2t-2)p_{j-1}}\\
s_{(2t-1)} &=& e_{ p_0 }\alpha^{ (2t-1)p_0 } &+& e_{ p_1 }\alpha^{(2t-1)p_1} &+& \cdots &+& e_{p_{j-2}}\alpha^{(2t-1)p_{j-2}} &+& e_{p_{j-1}}\alpha^{(2t-1)p_{j-1}}\\
\end{array}
\right.
\end{eqnarray}
結論から書くと、$j=t$から1つずつ$j$の値を小さくしていき、次の行列式が最初に0以外の値になったときの$j$の値がエラーの数になります。
\begin{vmatrix}
s_0 & s_1 & \ldots & s_{j-1} \\
s_1 & s_2 & \ldots & s_{j} \\
\vdots & \vdots & \ddots & \vdots \\
s_{j-1} & s_{j} & \ldots & s_{ 2j-2 } \\
\end{vmatrix}
なぜそうなるのか。
この行列式を次のように変形します。どうやってこの等式を導き出したのかもはやわかりませんが、計算してみるとたしかに合っています。
\begin{vmatrix}
s_0 & s_1 & \ldots & s_{j-1} \\
s_1 & s_2 & \ldots & s_{j} \\
\vdots & \vdots & \ddots & \vdots \\
s_{j-1} & s_{j} & \ldots & s_{ 2j-2 } \\
\end{vmatrix}
=
\begin{vmatrix}
1 & 1 & \cdots & 1\\
\alpha^{p_0} & \alpha^{p_1} & \cdots & \alpha^{p_{j-1}}\\
\vdots & \vdots & \ddots & \vdots\\
\alpha^{p_0(j-1)} & \alpha^{p_1(j-1)} & \cdots & \alpha^{p_{j-1}(j-1)}\\
\end{vmatrix}
\times
\begin{vmatrix}
e_{p_0} & 0 & \cdots & 0\\
0 & e_{p_1} & \cdots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \cdots & e_{p_{j-1}}\\
\end{vmatrix}
\times
\begin{vmatrix}
1 & \alpha^{p_0} & \cdots & \alpha^{p_0(j-1)}\\
1 & \alpha^{p_1} & \cdots & \alpha^{p_1(j-1)}\\
\vdots & \vdots & \ddots & \vdots\\
1 & \alpha^{p_{j-1}} & \cdots & \alpha^{p_{j-1}(j-1)}\\
\end{vmatrix}
右辺の両端の行列式は$0$になることはありません。
なので、この行列式が$0$になるということは、右辺真ん中の行列式が$0$になるということです。
右辺真ん中の行列式を計算してみると次のようになります。
\begin{vmatrix}
e_{p_0} & 0 & \cdots & 0\\
0 & e_{p_1} & \cdots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \cdots & e_{p_{j-1}}\\
\end{vmatrix}
=
e_{p_0}e_{p_0}\ldots e_{p_{j-1}}
$j$をエラーの数よりも大きく設定すると、$e_{p_0}e_{p_0}\ldots e_{p_{j-1}}$の中に$0$が混ざることになり、結果として行列式が$0$になります。
そのため、$j=t$から1つずつ$j$の値を小さくしていき、行列式が$0$以外になったときの$j$の値がエラーの数になります。
エラーの位置を特定する
ここでは次の式を考えます。
f(z) = w_{j}z^{j} + w_{(j-1)}z^{(j-1)} + w_{(j-2)}z^{(j-2)} + \cdots + w_{2}z^{2} + w_{1}z^{1}+1
$j$次の式なので解が最大$j$個あるはずですが、この解がエラー位置に対応する$\alpha$の逆数(つまり$\alpha^{-p_0},\alpha^{-p_1},\cdots ,\alpha^{-p_{j-2}},\alpha^{-p_{j-1}}$)となるような$w_j, w_{j-1}, \ldots, w_1$を求めます。
$w_j, w_{j-1}, \ldots, w_1$をうまく求められれば、$z$に$1, \alpha^{-1},\alpha^{-2},\cdots,\alpha^{-(n-1)}$を順次入力していき、$0$になるものがあればそれがエラー位置だ!という寸法です。
さて、$w_j, w_{j-1}, \ldots, w_1$の求め方ですが、ここでは結論だけ…。
頑張って展開すると成り立つはずです。
ちなみに、左辺の右側の行列は、エラーの数を求めるときに出てきた行列式と中身が同じですね。
\begin{pmatrix}
w_{j} & w_{(j-1)} & w_{(j-2)} & \cdots & w_{2} & w_{1}
\end{pmatrix}
\begin{pmatrix}
s_0 & s_1 & \ldots & s_{j-1} \\
s_1 & s_2 & \ldots & s_{j} \\
\vdots & \vdots & \ddots & \vdots \\
s_{j-1} & s_{j} & \ldots & s_{2j-2} \\
\end{pmatrix}
=
-1
\times
\begin{pmatrix}
s_{j} \\
s_{j+1} \\
\vdots \\
s_{2j-1}
\end{pmatrix}
エラーの内容を特定する
ここまでで、求めるエラーの数と位置、つまり、$\boldsymbol{e}$の中のどの要素を未知数とすればよいのかが分かりました。
未知数の数が減ったので、$\boldsymbol{s^{\mathrm{T}}} = \boldsymbol{e^{\mathrm{T}}} \times \boldsymbol{H}$から求められるようになりました。
具体的には、以下の式を解くことになります。
\begin{pmatrix}
1 & 1 & 1 & \ldots & 1 & 1 \\
\alpha^{ p_0 } & \alpha^{ p_1 } & \alpha^{ p_2 } & \ldots & \alpha^{p_{j-2}} & \alpha^{p_{j-1}} \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
\alpha^{(j-2) p_0 } & \alpha^{(j-2) p_1 } & \alpha^{(j-2) p_2 } & \ldots & \alpha^{(j-2) p_{j-2}} & \alpha^{(j-2) p_{j-1}} \\
\alpha^{(j-1) p_0 } & \alpha^{(j-1) p_1 } & \alpha^{(j-1) p_2 } & \ldots & \alpha^{(j-1) p_{j-2}} & \alpha^{(j-1) p_{j-1}} \\
\end{pmatrix}
\times
\begin{pmatrix}
e_{ p_0 } \\
e_{ p_1 } \\
\vdots \\
e_{p_{j-2}} \\
e_{p_{j-1}} \\
\end{pmatrix}
=
\begin{pmatrix}
s_0 \\
s_1 \\
\vdots \\
s_{(j-2)} \\
s_{(j-1)} \\
\end{pmatrix}
かなり長かったですが、検査行列$\boldsymbol{H}$からエラーの特定ができました!
生成行列
ここでやりたいことは、
\boldsymbol{m^{\mathrm{T}}}\times \boldsymbol{G}\times \boldsymbol{H} = \boldsymbol{O}
の$\boldsymbol{G}$を求めることです。
QRコードに格納するのは$\boldsymbol{m^{\mathrm{T}}}\times \boldsymbol{G}( = \boldsymbol{x^{\mathrm{T}}})$なので、$\boldsymbol{x}$には$\boldsymbol{m}$が含まれていなければならないという条件付きです。
いくら誤り訂正ができても、元のデータが分からなければ意味がないですからね。
で、今回は$\boldsymbol{G}$を求めるのではなく、$\boldsymbol{m}$から$\boldsymbol{x}$を求めることを考えてみます。
(理論的には$\boldsymbol{G}$は存在するはずですが…。)
リード・ソロモン符号となる条件
まずは、$\boldsymbol{x}$がリード・ソロモン符号となる条件を考えてみましょう。
\boldsymbol{x^{\mathrm{T}}}\times \boldsymbol{H} = \boldsymbol{O}
を盛大に展開すると、次の式になります。
この方程式をすべて満たす$\boldsymbol{x}$がリード・ソロモン符号というわけです。
\begin{eqnarray}
\left\{
\begin{array}{l}
x_0 &+& x_1 &+& \cdots &+& x_{n-2} &+& x_{n-1} &=& 0 \\
x_0 &+& \alpha x_1 &+& \cdots &+& \alpha^{n-2} x_{n-2} &+& \alpha^{n-1}x_{n-1} &=& 0 \\
\vdots\\
x_0 &+& \alpha^{(2t-2)} x_1 &+& \cdots &+& \alpha^{(2t-2)(n-2)} x_{n-2} &+& \alpha^{(2t-2)(2n-1)}x_{n-1} &=& 0 \\
x_0 &+& \alpha^{(2t-1)} x_1 &+& \cdots &+& \alpha^{(2t-1)(n-2)} x_{n-2} &+& \alpha^{(2t-1)(2n-1)}x_{n-1} &=& 0 \\
\end{array}
\right.
\end{eqnarray}
これらの方程式を共通化すると、以下のようになります(エラー位置特定で出てきた$f(z)$とは無関係です)。
f(z) = z^0 x_0 + z^1 x_1 + \cdots + z^{n-2} x_{n-2} + z^{n-1}x_{n-1} = 0
混乱してしまいそうになりますが、ここでは$\boldsymbol{x}$は決まった値なので、$f(z)$は$z$を変数に持つ単純なn-1次の多項式です。
$z$に$\alpha^0, \alpha^1, \cdots , \alpha^{2t-2}, \alpha^{2t-1}$をそれぞれ入れていくと、元の式になりますね。
ということは、$\alpha^0, \alpha^1, \cdots , \alpha^{2t-2}, \alpha^{2t-1}$は$f(z) = 0$の解なので、以下のように変形できるはずです。
f(z) = (z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})Q(x)
$Q(x)$は$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$を括りだした残りを適当に置いているだけなので気にしなくていいです。
注目すべきは、$f(z)$は$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$で割り切れるという点です。
これを満たしていれば、$\boldsymbol{x}$はリード・ソロモン符号です。
リード・ソロモン符号の生成
条件が分かったところで、その条件を満たすように$\boldsymbol{m}$からリード・ソロモン符号$\boldsymbol{x}$を作ってみましょう。
まず、$\boldsymbol{m}$から以下の関数を作ります。$k$は$\boldsymbol{m}$の長さ(バイト数)です。
m(z)=z^0 m_0 + z^1 m_1 + \cdots + z^{k-2} m_{k-2} + z^{k-1}m_{k-1}
これをいろいろ変形して先ほどの$f(z)$の形に持っていく方針で行きます。
$f(z)$はn-1次関数だったので、まず次数を揃えるために両辺に$z^{n-k}$を掛けます。
かなり前に出てきましたが$n-2t = k$だったので、$z^{n-k} = z^{2t}$です。
z^{2t}m(z)=z^{2t}m_0 + z^{2t+1} m_1 + \cdots + z^{2t+k-2} m_{k-2} + z^{2t+k-1}m_{k-1}
次数が揃ったので、$f(z)$を意識しておもむろに右辺を$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$で割ってみます。
商を$Q(z)$, 余りを$R(z)$とすると、
z^{2t}m(z) = (z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})Q(z)+R(z)
$R(z)$を左辺に移動させると…
z^{2t}m(z) - R(z) = (z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})Q(z)
右辺がまさに$f(z)$になるじゃないですか!
つまり、$z^{2t}m(z) - R(z)$はリード・ソロモン符号の条件を満たしています。
ではこの$z^{2t}m(z) - R(z)$の内容を詳しく見て見るために、$R(z)$について考えてみましょう。
$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$の次数は$2t$なので、$R(z)$の次数はは$2t-1$以下です。
そのため、以下のように書けます。
R(z)=r_0 z^0 + r_1 z^1 + \cdots + r_{2t-2} z^{2t-2} + r_{2t-1} z^{2t-1}
なので、$z^{2t}m(z) - R(z)$は以下のようになります。
z^{2t}m(z) - R(z) = -r_0 z^0 - r_1 z^1 - \cdots - r_{2t-2} z^{2t-2} - r_{2t-1} z^{2t-1} + m_0 z^{2t} + m_1 z^{2t+1} + \cdots + m_{k-2}z^{2t+k-2} +m_{k-1}z^{2t+k-1}
これと、
\begin{align}
f(z) &= z^0 x_0 + z^1 x_1 + \cdots + z^{n-2} x_{n-2} + z^{n-1}x_{n-1} \\
&= x_0 z^0 + x_1 z^1 + \cdots + x_{n-2} z^{n-2} + x_{n-1} z^{n-1} \\
&= x_0 z^0 + x_1 z^1 + \cdots + x_{n-2} z^{2t+k-2} + x_{n-1} z^{2t+k-1}
\end{align}
は対応するので、
\boldsymbol{x} = (-r_0,-r_1, \cdots , -r_{2t-2},-r_{2t-1}, m_0,m_1, \cdots ,m_{k-2},m_{k-1})
ということです。
なんと、$\boldsymbol{m}$がそのまま含まれてるじゃないですか!
そして、$(-r_0,-r_1, \cdots , -r_{2t-2},-r_{2t-1})$すなわち、「$\boldsymbol{m}$に対応する多項式に$z^{2t}$を掛けて、$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$で割ったときの各項の係数」が誤り訂正符号です!!
ガロア体
さて、誤り訂正符号の求め方を解説してきましたが、
このまま実装するのは大変です。$t=10$とかなっているときに$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$なんてまともに展開したいですか?
そこで、実際は「ガロア体」というものを利用して比較的簡単に実装できるようにしています。
ガロア体は、ざっくりいうと四則演算ができる有限集合です。
ここでいう四則演算のルールは普通のやつでなくても、独自に定義したもので大丈夫です。
ガロア体であるための条件はいろいろありますが、割愛しちゃいます。
一例を出すと、${0, 1}$は2進数的な演算を考えるとガロア体になります($GF(2)$という名前が付いています)。
$1+1 = 0$, $0-1 = 1$, $1 \times 1 = 1$といった具合です。
このガロア体、何が便利かって、有限集合なので計算するときに有限個の値しか出てこないんです。
同じ結果が得られるなら、無限個の値が出てくる実数の世界で計算するより、有限個の値しか扱わないでいいガロア体の世界で計算したほうが簡単だよね、ということです。
ちなみに、リード・ソロモン符号で使われるガロア体には、256個の値しか出てきません。1バイトのすべての値を表すのにぴったりな数ですね。
ガロア拡大体
そのガロア体はガロア拡大体$GF(2^8)$と呼ばれるのですが、なんと多項式の集合になります。
具体的には、係数が$GF(2)$で、(最高)次数が7の多項式の集合です。
つまり、以下のように1バイトの範囲で取りうる値が一対一で$GF(2^8)$の各要素に紐付けられます。
(00000000) \to 0\alpha^7 + 0\alpha^6 + 0\alpha^5 + 0\alpha^4 + 0\alpha^3 + 0\alpha^2 + 0\alpha + 0 \\
(00000001) \to 0\alpha^7 + 0\alpha^6 + 0\alpha^5 + 0\alpha^4 + 0\alpha^3 + 0\alpha^2 + 0\alpha + 1 \\
\vdots \\
(11111111) \to 1\alpha^7 + 1\alpha^6 + 1\alpha^5 + 1\alpha^4 + 1\alpha^3 + 1\alpha^2 + 1\alpha + 1 \\
ところで、ガロア体は四則演算可能なのでした。
足し算は問題ありません。
係数が$GF(2)$なので、各項の係数同士を足しても$GF(2)$に収まります。
例えば、次のような感じです。
(1\alpha^7 + 0\alpha^6 + 0\alpha^5 + 1\alpha^4 + 0\alpha^3 + 1\alpha^2 + 1\alpha + 1) + (1\alpha^7 + 1\alpha^6 + 0\alpha^5 + 0\alpha^4 + 1\alpha^3 + 0\alpha^2 + 0\alpha + 1) = 0\alpha^7 + 1\alpha^6 + 0\alpha^5 + 1\alpha^4 + 1\alpha^3 + 1\alpha^2 + 1\alpha + 0
しかし、掛け算をしようとするとこのままでは問題が…。
7次の多項式同士を掛け算すると14次の項が出てくる可能性がありますよね。
そこで、$\alpha$を次のように定義します。
\alpha^8+\alpha^4+\alpha^3+\alpha^2+1=0
そうすると$\alpha^8=\alpha^4+\alpha^3+\alpha^2+1$となるので、8次以上の項はこれを使って7次以下に落とすことができます。
かなり雰囲気的な説明になってしまいましたが、ちゃんと四則演算可能な気がしますよね(実際可能なんですが)。
αを10進数の世界と紐付ける
唐突ですが、$\alpha^0$から$\alpha^{255}$までを$\alpha^8=\alpha^4+\alpha^3+\alpha^2+1$を使って7次以下に落とし、対応するビット列、さらにその10進数表現を見ていきましょう。
| α | 7次以下に落とす | 対応するビット列 | 10進数表現 |
|---|---|---|---|
| $\alpha^0$ | $1$ | (0,0,0,0,0,0,0,1) | 1 |
| $\alpha^1$ | $\alpha$ | (0,0,0,0,0,0,1,0) | 2 |
| $\alpha^2$ | $\alpha^2$ | (0,0,0,0,0,1,0,0) | 4 |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $\alpha^7$ | $\alpha^7$ | (1,0,0,0,0,0,0,0) | 128 |
| $\alpha^8$ | $\alpha^4+\alpha^3+\alpha^2+1$ | (0,0,0,1,1,1,0,1) | 29 |
| $\alpha^9$ | $\alpha^5+\alpha^4+\alpha^3+\alpha$ | (0,0,1,1,1,0,1,0) | 58 |
| $\alpha^{10}$ | $\alpha^6+\alpha^5+\alpha^4+\alpha^2$ | (0,1,1,1,0,1,0,0) | 116 |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $\alpha^{254}$ | $\alpha^7+\alpha^3+\alpha^2+\alpha$ | (1,0,0,0,1,1,1,0) | 142 |
| $\alpha^{255}$ | $1$ | (0,0,0,0,0,0,0,1) | 1 |
途中省略していますが、$\alpha^0$から$\alpha^{254}$までに出てくるビット列はすべてユニークです。
そして、$\alpha^{255} = 1$ということは、ここから先はループするということを表しています。
ガロア体をリード・ソロモン符号の計算に使う
今まで出てきた数式の中で、いたるところに$\alpha$が出てきました。
これを$GF(2^8)$の$\alpha$として考えていきます。
例えば、$(z-\alpha^0)(z-\alpha^1) \cdots (z-\alpha^{2t-2})(z-\alpha^{2t-1})$なんかもまともに展開すると各項の係数がスゴいことになりますが、
$GF(2^8)$で計算すると、例えば$t=5$のときは次のようにスッキリします。
z^{10}+\alpha^{251}z^9+\alpha^{67}z^8+\alpha^{46}z^7+\alpha^{61}z^6+\alpha^{118}z^5+\alpha^{70}z^4+\alpha^{64}z^3+\alpha^{94}z^2+\alpha^{32}z^1+\alpha^{45}z^0
こんな感じでどんどん演算していけば、誤り訂正符号付きデータである$\boldsymbol{x} = (-r_0,-r_1, \cdots , -r_{2t-2},-r_{2t-1}, m_0,m_1, \cdots ,m_{k-2},m_{k-1})$も、それぞれ$\alpha^0$から$\alpha^{254}$を使って表せます。
そして最後に、先ほど出した表から対応する10進数表現を参照すれば、QRコードに格納する実際の値が得られます!
データの格納
ようやくQRコードに格納すべきデータが求められるようになりました。
あとはデータを格納するだけです。
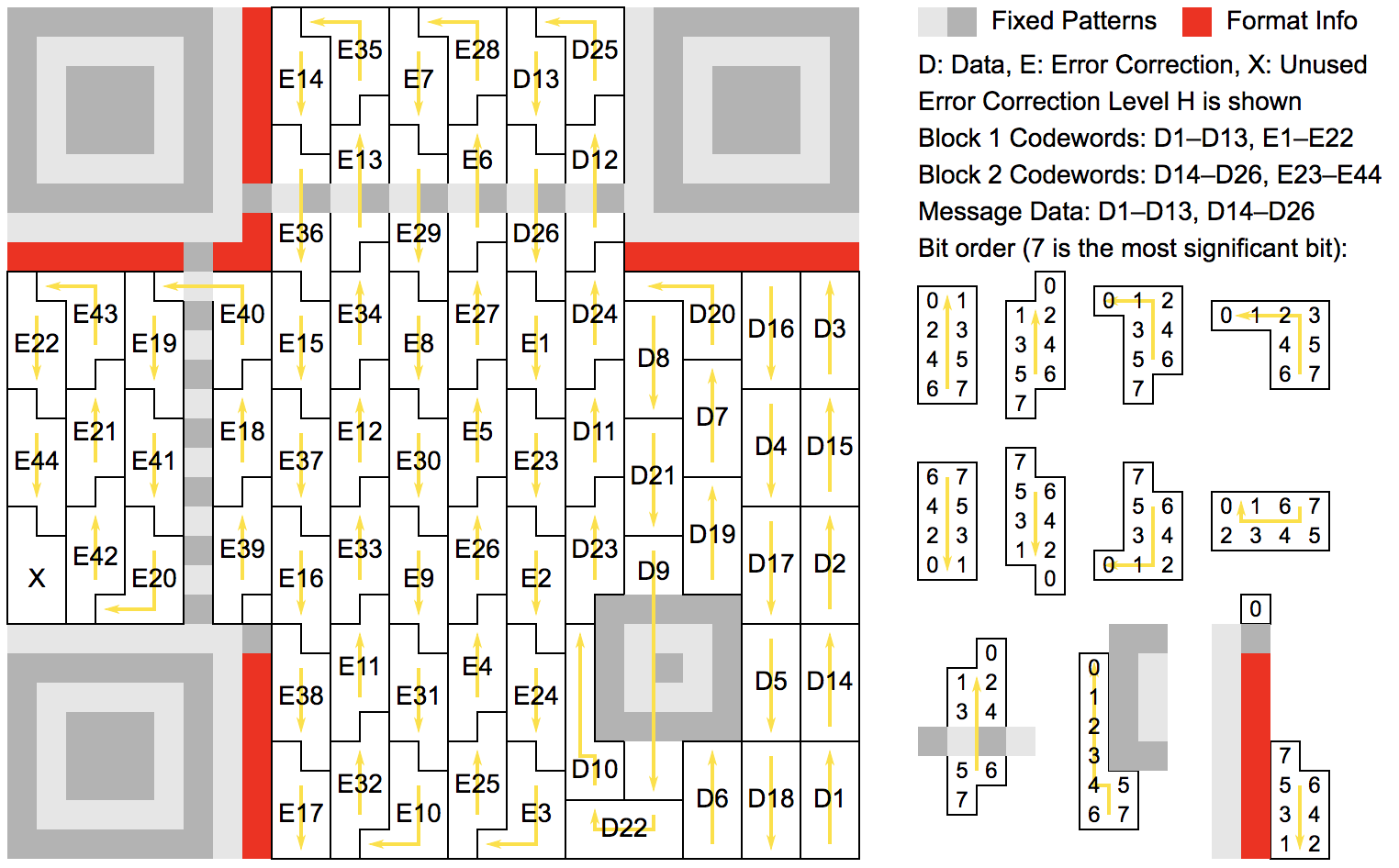
データの配置
格納データに対して一気に誤り訂正符号をくっつけようとすると計算が大変なことになるので、分割して計算していきます。
例としてバージョン3、誤り訂正レベルH(30%)の場合を見てみましょう。
格納できるデータ量や分割数、分割したデータに対する誤り訂正符号の長さなどは、バージョンと誤り訂正レベルごとに仕様で定められていますが、
今回の例の場合は、格納できるデータ量は26バイト、分割数が2です。分割した各13バイトにそれぞれ22バイトの誤り訂正符号が付きます。
分割したデータとそれに対する誤り訂正符号を合わせてRSブロックと呼びます。
格納できるデータ量は誤り訂正符号含めては70バイト、そのうち純粋なデータは26バイトです。
これを2つに分割して13バイトずつとし、それぞれ誤り訂正符号を計算します。
RSブロックのデータ、誤り訂正ブロックの各バイトに以下のように名前を付けます。
| RSブロック | データ | 誤り訂正符号 |
|---|---|---|
| 1 | D1, D2, ..., D13 | E1, E2, ..., E22 |
| 2 | D14, D15, ..., D26 | E23, E24, ..., E44 |
これを配置していくのですが、単純に並べるわけではないんです。
RSブロック1の1番目のデータバイト、RSブロック2の1番目のデータバイト、...、RSブロックnの1番目のデータバイト、
RSブロック1の2番目のデータバイト、RSブロック2の2番目のデータバイト、...、RSブロックnの2番目のデータバイト、
...
RSブロック1の1番目の誤り訂正バイト、RSブロック2の1番目の誤り訂正バイト、...、RSブロックnの1番目の誤り訂正バイト、
RSブロック1の2番目の誤り訂正バイト、RSブロック2の2番目の誤り訂正バイト、...、RSブロックnの2番目の誤り訂正バイト、
...
という順番で格納していきます。
推測ですが、こうやって各RSブロックを分散して配置することで読み取り不可になる可能性を下げようとしているのではないかと思います。
単純に並べてしまうとRSブロックのバイト同士が近くなるので、例えばインクがポタっと落ちたりしたら一発で読み取り不可になったり。
今回の例の具体的な格納場所は英語版のWikipediaにあります。
マスクの適用
単純にデータを格納しただけでは、位置検出パターンに似た模様が出現したり、白黒のバランスが悪くなったりして読み取り性能に悪影響を及ぼす可能性があります。
そのような事態を防ぐため、適当なパターンでマスクします。
マスクパターンは以下の8種類が用意されています。
| マスクパターン参照子 | マスク条件 |
|---|---|
| 000 | (i+j) mod 2 = 0 |
| 001 | i mod 2 = 0 |
| 010 | j mod 3 = 0 |
| 011 | (i+j) mod 3 = 0 |
| 100 | ((i div 2) + (j div 3)) mod 2 = 0 |
| 101 | (ij) mod 2 + (ij) mod 3 = 0 |
| 110 | ((ij) mod 2 + (ij) mod 3) mod 2 = 0 |
| 111 | ((ij) mod 3 + (i + j) mod 2) mod 2 = 0 |
実際にどんなパターンになるかも、英語版のWikipediaにありました。
(式が若干違いますが、結果は同じです。)

どのマスクパターンを選択するかは、実際にそれぞれ適用してみて望ましくないパターンに失点を与えることで評価します。
具体的には、以下の条件を満たすと失点になります。
| 特徴 | 評価条件 | 失点 |
|---|---|---|
| 同色の行/列の隣接モジュール | 長さ5以上 | 5を超えた長さ + 3 |
| 同色のモジュールブロック | ブロックサイズ 2×2 | ブロック数 x 3 |
| 行/列における1:1:3:1:1(暗:明:暗:明:暗)のパターン | 存在 | 40 |
| 全体に占める暗モジュールの割合 | 50%から5%以上離れたとき | 5%刻み x 10 |
形式情報・型番情報格納
形式情報
形式情報は誤り訂正レベルとマスクパターン参照子からなります。
誤り訂正レベルは訂正できるエラーの数を決めます。レベルは4つ用意されています。
| 誤り訂正レベル | 2進指示子 | 許容欠損 |
|---|---|---|
| L | 01 | 7% |
| M | 00 | 15% |
| Q | 11 | 25% |
| H | 10 | 30% |
マスクパターン参照子は先に示したとおりです。
この2つをつなげて5ビットにして、BCH符号という別の誤り訂正符号を求めて15ビットにします。
さらにこの15ビットがすべて0にならないように特定のビットパターン(101010000010010 : 0x5412)との排他的論理和を取ったものを格納します。
型番情報
型番情報はバージョン7以上のQRコードに入ります。
型番情報は6ビット、BCH符号によって12ビットになります。
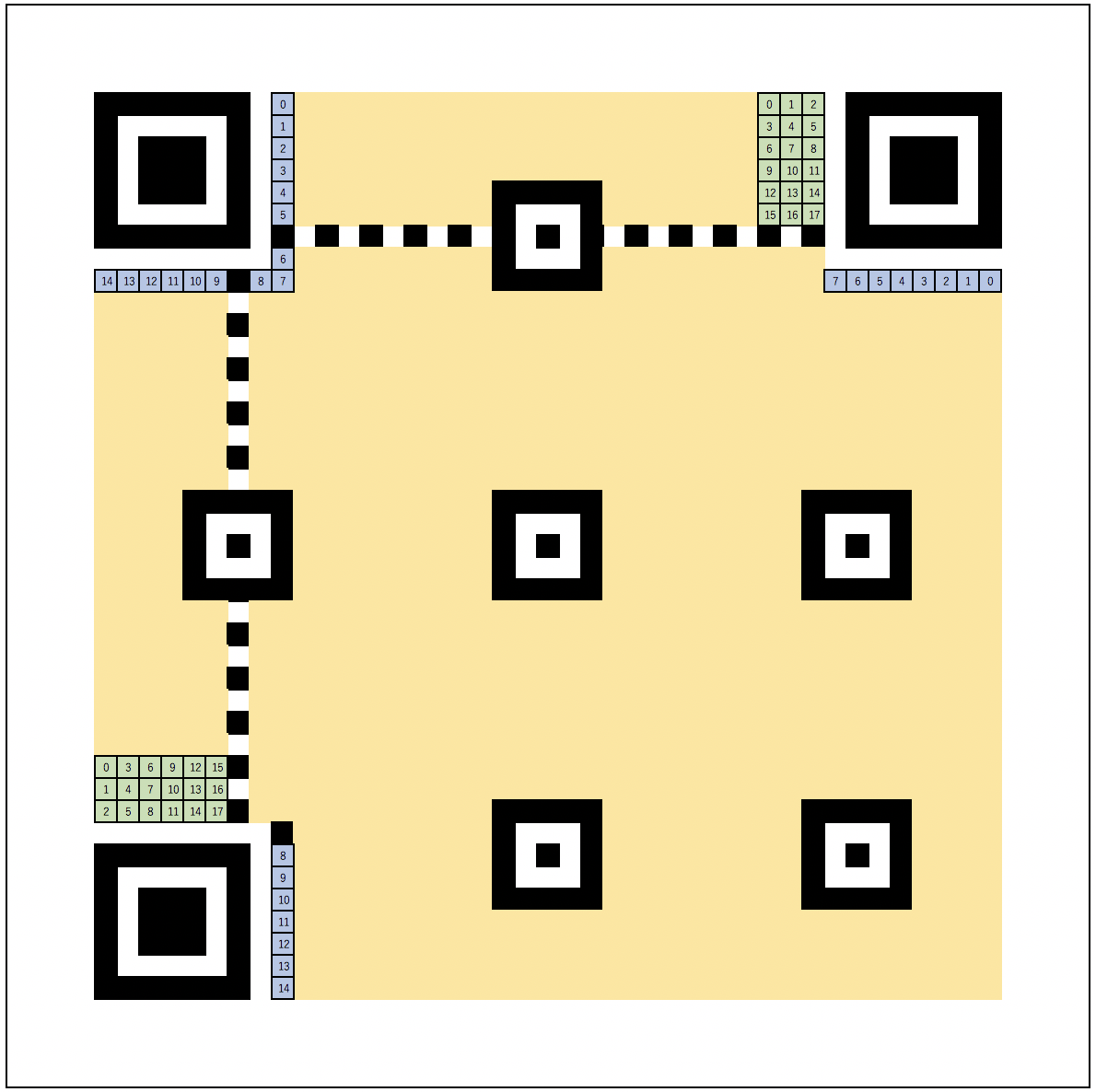
格納位置
型番情報、形式情報はそれぞれQRコードの以下の位置に2箇所に冗長化して配置されます。
余談
以上で解説はすべて終了ですが、QRコードの秘密を知った皆様は、新たな遊びを得ることができました。
その名もQR山崩し。
- 適当なQRコードを用意します。
- 適当にセルを塗りつぶします(どれだけ塗りつぶしてもOK)。
- QRコードリーダーで読み取ります。
- 読み取れればターン交代。2.に戻ります。
- 読み取れなければ負け。
どのような仕組みで誤り訂正が行われているかを知っていると、より楽しめると思います ![]()
まとめ
ところどころ説明を省略したにも関わらずかなり長くなってしまいましたが、いかがだったでしょうか?
普段何気なく使っているQRコードですが、裏では結構大変な処理をしていました。
今後QRコードを目にしたときに、これらの処理に思いを馳せてもらえたら幸いです。