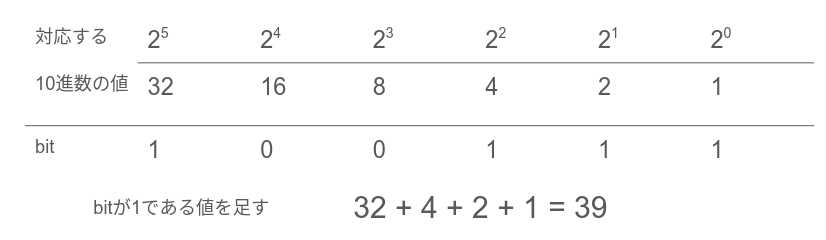LoginSignup
9
0

More than 1 year has passed since last update.

木更津高専Advent Calendar 2021Day 14
@chizuchizu

あーー　IPアドレスを2進数に変換したいな〜〜　でも面倒だなぁ

Last updated at Posted at 2021-12-13

この記事は木更津高専アドベントカレンダー14日目の記事です。昨日の記事は @takamasa272 氏による学寮ネット委員 珍事件簿
ですっ！

はじめまして、木更津高専1年情報工学科のチズチズと申します。

したこと

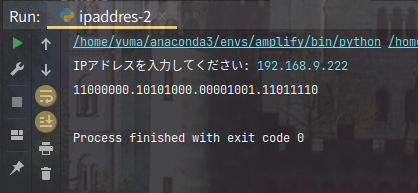
10進数で表されるIPv4のIPアドレスを2進数に変換しました。
普通に計算するだけでは面白くないので、ナウいアニーリングマシンというものを使って解きます。

image.png

先に断っておきます。今回使用するのはイジングマシンよりのアニーリングマシンなので、広義のアニーリングとは異なることに注意してください。

IPアドレスとは

「192.168.1.1」といった文字列、どっかで見たことあるような……
IPアドレスはコンピュータが持つ固有の規格です。IPアドレスの中でも今回使うIPv4という規格は32bitで構成されています。

32文字の0と1の文字列は長すぎるので、8bitずつ区切って10進数(0~255)で表すことが多いです。

動機

1週間前に受けた専門教科のテストでIPアドレスを2進数に変換しろという問題が出てきたから。

アプローチ

10進数と2進数の相互変換

image.png

2進数から10進数の変換は上の図で表すように、ビットの値一つ一つに対応する$2^n$の値を掛けて足し合わせることで実現できます。

2進数で表示されたビット列は1か0しかないので、何も考えずに掛けて足してという行為で簡単に10進数に戻すことができます。

ちなみに、このような操作は基数操作と呼ばれています。基数とは、10進数の10、2進数の2にあたります。

ところで、10進数から2進数への基数変換はどうしたらよいでしょうか。

ネットで調べれば、色々なやり方が紹介されています。一番有名なのは10進数の値を2で割り続けていったときの余りをメモする方法だと思います。本記事では触れないので興味がある読者は検索してみてください！

提案手法

image.png

2進数のビット列の一つ一つを0と1をとる2値変数とみて、2進数を10進数に基数変換したときと同じことをしました。2値変数に対応する$2^n$の値を掛けて足し合わせた多項式（変数を使っているので）が何かしらの値と等しくなればいいんですよね？？

でもこんな方程式？解けないよ〜　教わってないよ〜〜
そんな方にアニーリングをオススメしたい！

アニーリングとは

最適解の探索を行うアルゴリズムです。　←　最適解？？？

超ざっくりいうと2値変数を使った多項式を解いてくれるアルゴリズムです。

これはちょっと語弊があって、ちょっとだけ厳密に書くと2値変数の2次多項式で表された関数の最小値を探索するアルゴリズムを指します。これをQUBO(二次制約なし二値最適化)と呼びます。こんな式で定式化されていたりします。パラメータ$q$に関する二次の項と一次の項があるのがわかると思います。この多項式で表された関数を最小化するようなパラメータ$q$を探索しています。

H = \sum_{i \neq j} J_{ij} q_i q_j + \sum_{i}  q_{i} \qquad (q = \{0, 1\})

外野「ん？？　QUBOは制約なしやんけ！！」

制約を制約なしの形に変換する方法があるので問題ないです。

アニーリングについての補足

量子アニーリングとは違うの？

違います。今回は量子アニーリングは使いません。

使えるビット数や、性能（これは主観）において古典的なアニーリングマシンのほうがパフォーマンスが良いので量子アニーリングは使いません。動かすことはできますが、普段使ってないのでアニーリングマシンを採用！

H = \sum_{i \neq j} J_{ij} \sigma_i \sigma_j + \sum_{i}  \sigma_{i} \qquad (\sigma = \pm 1)

これはイジング模型のエネルギー関数と呼ばれる式です。QUBOとよく似ていますね。量子アニーリングはQUBOをイジング模型に変換して、実験→測定を通して解を得る作業を指します。
一方でアニーリングマシンはシミュレーテッドアニーリングと呼ばれる古典的な手法を並列化、高速化した専用ハードウェアのことを指します。

シミュレーテッドアニーリングに量子要素は一切ありません！

理論的な話はFixstars社によるアニーリングマシンとイジング模型に関する詳しい解説を参照してみてください。

>

実装するぞ！

本記事ではFixstars Amplify SDKというライブラリを用いて定式化からアニーリングマシンとの通信、解の後処理を行います。

Fixstars Amplify SDKについて

image.png
https://amplify.fixstars.com/ja/sdk#workflow より

Fixstars Amplify SDK(以下Amplify)は、
- 定式化の支援
- ハードウェアとの接続と通信

といったことをしてくれます。何が凄いかというと、今まではアニーリングマシンを開発している会社がそのマシンに対応したSDKを開発していたため、使いたい人はマシンに対応したSDKごとにコードを書き直す必要がありました。しかし、Amplifyはどんなハードウェア（アニーリングマシン）を使う人でも定式化のコードは同じになります。ハードウェアが抽象化されているので、ドキュメントに書いてある通りトークン、パラメータ設定してあげるだけで簡単に計算することができます。

Fixstars社はこのSDKのみならず、Amplify AEと呼ばれるアニーリングマシンも開発しています。このマシンの使い勝手が非常に良いので、本記事ではAmplify AEで計算を行います。

Amplifyを使ったこと無い人向けインストールチュートリアル

ここからはAmplifyのドキュメントを参考に書いています。

対応マシン
- Windows（WSL上じゃないと動きません）
- Mac（M1には対応していません）
- Linux

適当な仮想環境で以下のようにインストールするだけです。

pip install amplify

SDKを使うだけならこれで十分なのですが、Amplify AEを使うにはユーザー登録をしてAmplify AEのアクセストークンを入手する必要があります。
登録できたらログインしてアクセストークンを確認してください。このアクセストークンは公開してはいけません！Amplifyを使ったコードを公開するときには注意が必要です。アクセストークンの欄を適当な文字列*******で埋めるといった処理を施しましょう。（もしやらかしたらすぐアクセストークンを再発行すれば良さそう）

10進数から2進数への基数変換の定式化

制約: \sum_{i = 0}^{\lceil log_2 n \rceil} 2^i q_i  = n

10進数の$n$をi桁目が$q_i$で表される2進数に基数変換するときの制約です。等式の制約を使っていますね。

この制約は以下のような二乗誤差としてQUBOの定式化ができます。少し考えてみると、$H$が最小値である0になることと、2進数への基数変換ができていることが等価であることがわかります。機械学習の最小二乗法と同じノリです。

H = (\sum_{i = 0}^{\lceil log_2 n \rceil} 2^i q_i  - n) ^2

実装について

今回の問題設計

"192.168.2.222"といった文字列から２進数変換した""という文字列を返したいですよね。

  • 8bitごとに分割する
    • 最初は192を2進数にして、次は168...
    • 最後に"."区切りでjoinしてあげればよさそう
  • 2進数を8bitの2進数に変換する　←　これがメインpart

実装例
from amplify import Solver, BinarySymbolGenerator, BinaryMatrix
from amplify.client import FixstarsClient
from amplify.constraint import equal_to

import numpy as np

"""Amplifyの初期設定　はじまり"""
client = FixstarsClient()  # Amplify AEを使います宣言

client.token = "*******ここにトークンを入れてね*****"

client.parameters.timeout = 10  # 計算に使う時間 単位はms
# solverの定義
solver = Solver(client)
"""Amplifyの初期設定　おわり"""


# 解を得る関数
def get_weight(max_length, result):
    weight = np.zeros(max_length, dtype=np.int)
    item = result[0].values
    for i in range(max_length):
        if item.get(i) is not None:
            weight[i] = item[i]
        else:
            weight[i] = 0

    return weight


address = input("IPアドレスを入力してください: ")
# 最後、表示するのに使うリスト
ans_bits = []

for ad in address.split("."):  # .区切りで、8bitずつ取り出す
    # 10進数の値
    base_value = int(ad)

    # ビットを取り出すジェネレータの宣言
    gen = BinarySymbolGenerator()
    # 今回は8bitずつ取り出すので8に固定　←　普通に使う分にはint(1 + np.log2(n))でOK
    n_bits = 8

    # n_bits個の要素がある二値変数のリスト
    bits = gen.array(n_bits)

    # 二値変数の多項式
    poly = 0
    for i, bit in enumerate(bits):
        poly += bit * (2 ** i)  # 2^i q_i

    # 一番大事な制約の部分
    constraint = equal_to(poly, base_value)

    # 解く
    result = solver.solve(constraint)
    client_result = solver.client_result
    # 変数の値を取得
    binary_weight = get_weight(n_bits, result)

    # 今までbitがindex順(左から右)だったので反転させる(右から左にする)
    # 4の2進数表示
    # index順: 001
    # やりたいやつ: 100
    translated_bits = binary_weight[::-1]

    # bit列(list)をstrに変換してlistに追加
    ans_bits.append("".join(map(str, translated_bits)))

# .区切りでprint
print(".".join(ans_bits))

>

とにかく長いので大事な所をつまんで解説していきます。

まずはおまじないです。Amplify AEを使うならみんなこれ書いてます。clientの部分は流行り（？）のD-Waveマシンを選択することも可能です。1

client = FixstarsClient()  # Amplify AEを使います宣言

client.token = "*******ここにトークンを入れてね*****"

client.parameters.timeout = 10  # 計算に使う時間 単位はms
# solverの定義
solver = Solver(client)

変数を出したい時は、ジェネレータに欲しい変数の数を渡してあげるだけで、変数の入ったリストが返ってきます。なんでジェネレータかというと、今まで使った変数のindex情報がなくても新しい変数を取り出すことができるからです！2

# ビットを取り出すジェネレータの宣言
gen = BinarySymbolGenerator()
n_bits = 8

# n_bits個の要素がある二値変数のリスト
bits = gen.array(n_bits)
print(bits)

# [q_0, q_1, q_2, q_3, q_4, q_5, q_6, q_7]

bits_2 = gen.array(n_bits)
print(bits_2)

# [ q_8,  q_9, q_10, q_11, q_12, q_13, q_14, q_15]

Pythonだと値が決まってない変数を使うのに慣れないかもしれないです。でも、普通に四則演算ができ。

# 二値変数の多項式
poly = 0
for i, bit in enumerate(bits):
    poly += bit * (2 ** i)  # 2^i q_i

そして、適当に制約をつけてあげる！今回は基数変換なのでもちろん、等式制約ですよ！

# 等式制約
constraint = equal_to(poly, base_value)

# 不等式制約(poly >= base_value)
constraint = greater_equal(poly, base_value)

# 不等式制約(poly <= base_value)
constraint = less_equal(poly, base_value)

後は、解を取り出す作業になります。ソルバーに制約を投げると解の情報であるresultが返ってきます。それを後処理して、扱いやすくしています。
client_resultはアニーリングにかかった実行時間情報などを取り出すことができます。

result = solver.solve(constraint)
client_result = solver.client_result
binary_weight = get_weight(n_bits, result)  # get_weightは自分で作った関数

おわりに

アニーリングマシンは、使い方によって様々なことができます。数独を解いたり、機械学習をしたり……
今回紹介したのはごくごく一部の例なので、これをきっかけにアニーリングマシンに入門する人が出てきたら嬉しい限りです。

D-waveマシンを使って量子アニーリングで〇〇してみた！っていうタイトルにしても良かったのですが、扇動的すぎるし、普段D-wave使ってないくせに背伸びしたら怒られそうなのでこんな記事にしました。

  1. 富士通デジタルアニーラ、日立CMOSアニーラにも対応 ↩

  2. 昔はジェネレータがなくてindex情報が必要だったんですが、アップデートのおかげで便利になりました ↩

9
0
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
9
0