pythonとフェルマーの小定理で１行FizzBuzz

FizzBuzzでフェルマーの小定理が使えるらしい

フェルマーの小定理がFizzBuzzに使えると聞いて、調べてもわかりやすいコードと記事が見つけられなかったのでpythonで自分で作ってみました。以下のコードはできあがったものです。

for n in range(1,101):print("FizzBuzz"[n**2%3*4:12-n**2%3*4-n**4%5*8] or n)

※【2021/03/17追記】記事の初回投稿後にコメント欄などでの意見を参考に改良を試みましたが最終的に以下のコードを頂きました。

for n in range(1,101):print("FizzBuzz"[n*n%3*4:8-n**4%5*4]or n)

これを見ても普通はよくわからないと思うので作成時の思考過程をこの記事で書いていきます。

フェルマーの小定理

まずはフェルマーの小定理の主張を確認しましょう。

n^{p-1} ≡ 1 \quad (mod \hspace{5pt} p)

ただしpとnは互いに素で、pは素数。
$n^{p-1}$をpで割った余りが1になるということです。

※【2021/03/17追記】（読み飛ばし可能）$n^p≡n$と表現される場合がありますがnは自然数なので同値です。上記の表現のほうが今回は都合がいいです。また、より一般的な「オイラーの定理」（$n^{Φ(m)}≡1 $ (mod m)）への拡張（素数pに対してはトーシェント関数がΦ(p)=p-1）を考えても上の表記のほうが適しています。

FizzBuzzへの応用

nがp（3または5）の倍数でないとき、nとpは互いに素だから

n^{2} ≡ 1 \quad (mod \hspace{5pt} 3)\\
n^{4} ≡ 1 \quad (mod \hspace{5pt} 5)

が成り立ちます。
nがp（3または5）の倍数のとき、余りはもちろん0です。つまり3（または5）の倍数でないかどうかを1と0で表せるわけです。

実装

以下の式はnが3の倍数のとき0、そうでないとき1になります。

n**2%3

0と1を反転させたければ以下のようにします。

1-n**2%3

5も同様です。

n**4%5
1-n**4%5

これを利用すると次のようなFizzBuzzコードが書けます。

for n in range(1,101):print((1-n**2%3)*"Fizz"+(1-n**4%5)*"Buzz" or n)

文字列"FizzBuzz"からのスライス

上記のコードはn**2%3などが数字であることを活かしきれていません。これではつまらないので"FizzBuzz"という文字列から必要に応じて必要な部分だけをスライスするプログラムを実装してみます。

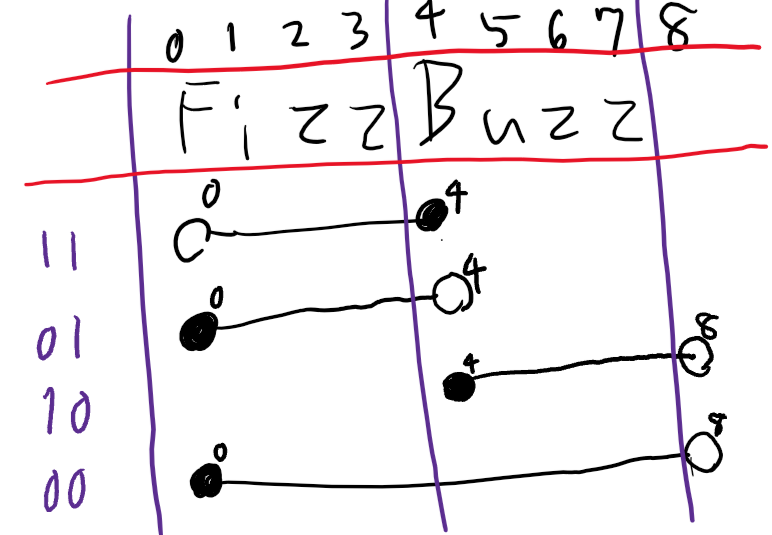
手書き失礼しました。
上の画像は"FizzBuzz"の各文字のインデックスとスライスの開始（黒丸）および終了（白丸）の対応で、上から順に数字、Fizz、Buzz、FizzBuzzの場合に相当します。紫の数字はn**2%3およびn**4%5を並べたものです。

スライスに含まれるのはは開始点のインデックス以上かつ終了点のインデックス未満のインデックスを持つ要素です。また、終了点のインデックスが開始点のインデックス以下になると文字列を返しません。したがって例えば上の画像のような開始・終了の位置が考えられます。

n**2%3およびn**4%5の値をベクトル(x,y)で表し開始点と終了点を(X,Y)で表すと

X = ax + by + c\\
Y=dx+ey+f

を満たすような6つのパラメータa,b,c,d,e,fを見つけます。上の図の通りだと拘束条件が8個で解は存在しない事になってしまいますが、(0,1)と(0,0)のときの開始点Xは4以下であればよく(1,0)と(0,0)のときの終了点Yは8以上であればよいので例えば(a,b,c,d,e,f)=(4,0,0,-4,-8,12)などを選びます。

X = 4x \\
Y=-4x-8y+12

このX,Yで"FizzBuzz"[X:Y]のようにスライスします。これを実装したのが冒頭のコード(以下に再掲)です。

for n in range(1,101):print("FizzBuzz"[n**2%3*4:12-n**2%3*4-n**4%5*8] or n)

追記：平方の記述(2019/04/27)

コードゴルフとしてはn**2ではなくn*nとしたほうがよいという指摘をいただきました。

for n in range(1,101):print("FizzBuzz"[n*n%3*4:12-n*n%3*4-n**4%5*8] or n)

追記2：n*n%3*4をまとめる(2019/04/28)

n*n%3*4が２回現れているのでoとして以下のようにまとめるとさらに2文字短くなるという指摘をいただきました。

for n in range(1,101):o=n*n%3*4;print("FizzBuzz"[o:12-o-n**4%5*8] or n)

追記3：Y=-4y+8とするとさらに短くなる(2021/03/16)

コメント欄で以下のコードでも良いことをご指摘いただきました。(x,y)=(1,1)のときY≦Xを満たせば良いので(X,Y)=(4,4)とするとYがyのみに依存する形になりコードがさらに8文字も短くなりました。これは数学的にもきれいです。

for n in range(1,101):print("FizzBuzz"[n*n%3*4:8-n**4%5*4]or n)