はじめに
Pythonのsetについて最近学習したので基本をまとめる。
set型とは
set型もシーケンスと似たデータ型で、リストのように複数の要素を保存できる。
(シーケンスとは、複数の要素を持つデータ型のこと。(例:リスト・タプルなど))
ではリストと何が違うのか。
setはリストと違い、中の要素が重複されないように管理される。
既にsetの中に存在する値を登録しようと思っても、新しい要素が追加されない。
また、インデックスを使って値を取り出すこともできない。
つまり、set型とは重複しない要素のグループを集合として扱うためのデータ型。
set型を使うことで複数の集合の集合演算ができる。
要素を集合として扱うため、setに要素の順番はない。
setの定義
setは要素に数値や文字列を追加できる。
setの定義は、**{}**を使用する。
ここで、集合numberに1〜6の整数を要素として定義してみる。
number = {1,2,3,4,5,6}
print(number)
{1, 2, 3, 4, 5, 6} #結果
ただし、リストや辞書は変更できてしまうため、setの要素にはできない。
list_num = [1,2,3]
set_num = {list_num,4,5,6}
TypeError: unhashable type: 'list' #結果
同様の理由からsetを別のsetの要素にすることもできない。
A_num = {1,2,3}
B_num = {A_num,4,5,6}
TypeError: unhashable type: 'set' #結果
ちなみに、重複した値を要素に指定して結果をみてみる。
number = {1,2,3,4,5,6,6}
pirnt(number)
{1, 2, 3, 4, 5, 6} #結果
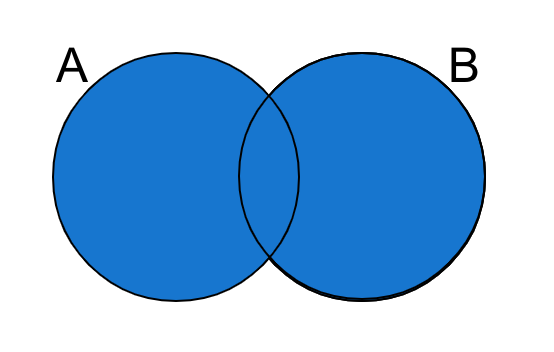
setの和集合
setの和集合を得る場合、|演算子を使用する。
和集合→+演算子を使いそうなところだが、
和集合の場合は重複した要素は足されないため論理和(OR)に近いため、この演算子を用いる。
実際に和集合を計算してみる。
prime = {2,3,5,7,11,13}
number = {1,2,3,4,5}
prime_number = prime | number
print(prime_num)
{1, 2, 3, 4, 5, 7, 11, 13} #結果
setの差集合
複数の集合の差集合を考える。
2つの集合A,Bを与えた時、集合Aから集合Bの要素を取り除く。
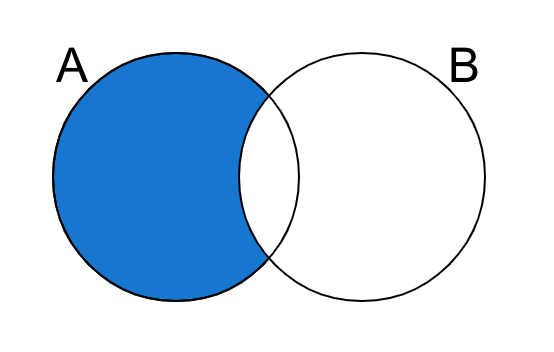
setの差集合を得る場合、-演算子を使用する。
実際に差集合を計算してみる。
number = {1,2,3,4,5,6}
even = {2,4,6,8,10}
odd_number = number - even
print(odd_number)
{1,3,5} #結果
setの交わり
複数の集合の交わりを考える。
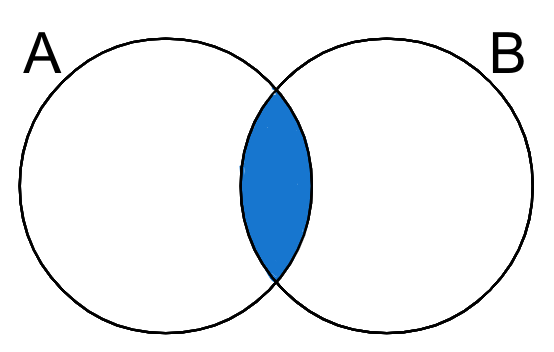
setの交わりを得る場合、&演算子を使用する。
実際に交わりを計算してみる。
number = {1,2,3,4,5,6}
even = {2,4,6,8,10}
even_number = number & even
print(even_number)
{2, 4, 6} #結果
setの対象差
複数の集合の対象差を考える。
2つの集合の対象差をとると、両方のsetに共通して含まれている要素だけを取り除いた要素の集合を得ることができる。
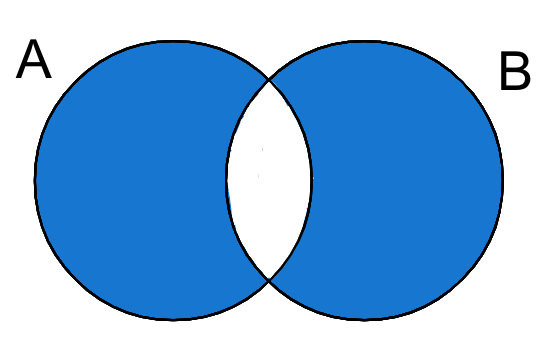
setの対象差を得る場合、^演算子を使用する。
実際に対象差を計算してみる。
dice = {1,2,3,4,5,6}
even = {2,4,6,8,10}
not_even_dice = dice ^ even
print(not_even_dice)
{1, 3, 5, 8, 10} #結果
リストからsetへの変換
組み込み関数**set()**を使うとリストをsetに変換することができる。
以下の結果から、setは「重複しない要素の集合」であること、「要素の順番はない」ということも確認できる。
list_alpha = ["A","B","C","D","E","E"]
set_alpha = set(list_alpha)
print(set_alpha)
{'E', 'C', 'A', 'D', 'B'} #結果
以上です。