素人が時系列データに対するフィルタ処理を行なってみた

はじめに

素人（数学的素養が中学卒業程度まで退化し、かつ、プログラミングを生業としていない残念な人）が趣味で時系列分析を行うにあたって、時系列データに対するフィルタ処理を行なってみる。ここで、フィルタに求める要件は以下の通り。

• 観測値からのノイズ除去を通じた真値の推測を目的としたフィルタリングを行う
• 中学卒業程度の数学の素養の元で処理内容を直感的に理解できること
• フィルタを利用するためのPythonベースでの実装を容易に実現出来ること
• フィルタにより得られた時系列内のある時点での値を算出するにあたって、その時点より未来のデータを入力値として用いないこと（過去から未来に向かう方向での逐次的なフィルタ処理を想定する）

利用するフィルタ

手間を惜しむため、出来合いのフィルタ（実装）を拝借する（先人の知恵に感謝）。
拝借する（そのまま用いる/改変して用いる）フィルタは以下の通り。

• 移動平均法
• ガウス畳み込み
• 一次遅れ系
• カルマンフィルタ

うち、前から三者については、「ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)」記事にてサンプルコードとして示される実装を拝借し、必要に応じて改変して用いる。

また、カルマンフィルタについては、FilterPyライブラリによる実装を拝借する。

フィルタの適用対象とするデータの準備

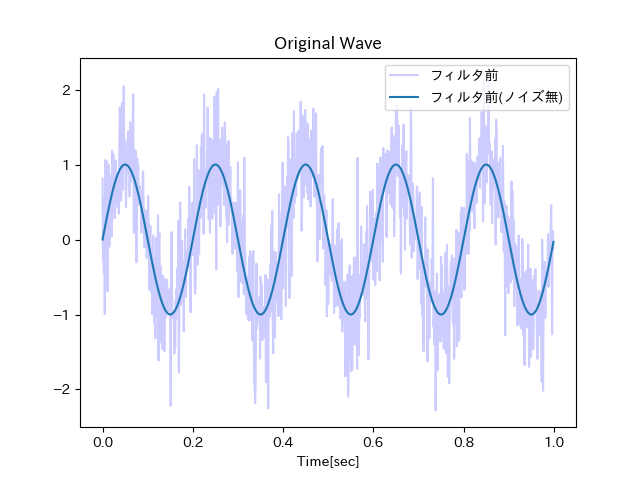
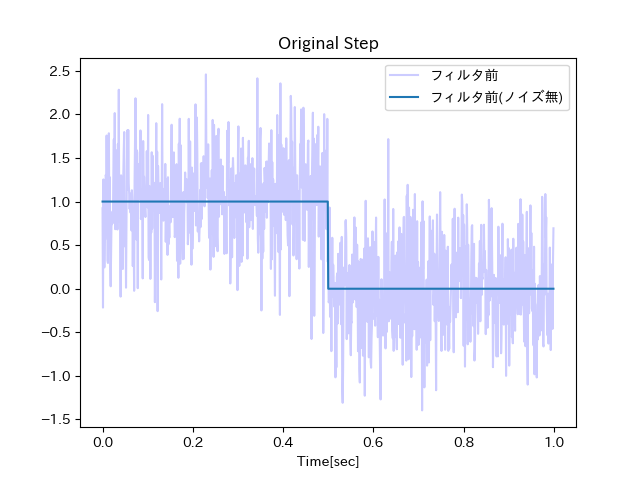
「ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)」記事で用いられている正弦波データ、および矩形波データをそのまま拝借する。

import numpy as np
import matplotlib.pyplot as plt

dt = 0.001 #1stepの時間[sec]
times  =  np.arange(0,1,dt)
N = times.shape[0]

f  = 5  #サイン波の周波数[Hz]
sigma  = 0.5 #ノイズの分散

np.random.seed(1)
# サイン波
x_s =np.sin(2 * np.pi * times * f) 
x = x_s  +  sigma * np.random.randn(N)
# 矩形波
y_s =  np.zeros(times.shape[0])
y_s[:times.shape[0]//2] = 1
y = y_s  +  sigma * np.random.randn(N)

正弦波データ

矩形波データ

各フィルタの実装

移動平均法、ガウス畳み込み、および一次遅れ系については「ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)」記事に示されるサンプルコードに基づく実装を行う。ただし、以下の2点の変更を加える。

• 今回の要件に適合するよう、過去から未来に向かう方向での逐次的なフィルタ処理を行う実装に改める（未来の観測値を過去時点におけるフィルタリングのために用いることは行わない）
  • ガウス畳み込みに対しては、畳み込みの際にガウシアンの左半分のみをカーネルとして用いる変更を行う（ものの、その妥当性については自信なし...）
• フィルタに引き渡すパラメーターを変更する（特に、各フィルタを用いたフィルタリング結果を重ねて比較するために、良い感じのパラメーターを適当にセットする）

移動平均法

「ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)」記事より実装を拝借、改変（中心化移動平均に代わって後方移動平均を利用するようロジックを改変）。

def LPF_MAM(x,times,tau = 0.01):
    k = np.round(tau /(times[1] - times[0])).astype(int)
    x_mean =  np.zeros(x.shape)
    N = x.shape[0]
    for i in range(N):
        if i == 0:
            x_mean[i] = x[0]
        elif  i-k < 0 :
            x_mean[i]  = x[: i].mean()
        else :
            x_mean[i]  = x[i-k : i].mean()
    return x_mean

tau_x = 0.02
tau_y = 0.02
x_MAM = LPF_MAM(x,times,tau_x)
y_MAM = LPF_MAM(y,times,tau_y)

ガウス畳み込み

「ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)」記事より実装を拝借、改変（畳み込みのために用いるカーネルとしてガウシアンの左半分のみを用いるようロジックを改変）。

def LPF_GC(x,times,sigma):
    sigma_k = sigma/(times[1]-times[0]) 
    kernel = np.zeros(int(round(3*sigma_k))*2+1)
    for i in range(kernel.shape[0]):
        kernel[i] =  1.0/np.sqrt(2*np.pi)/sigma_k * np.exp((i - round(3*sigma_k))**2/(- 2*sigma_k**2))
    
    kernel = np.delete(kernel, slice(kernel.shape[0]//2+1, kernel.shape[0]), None) # ガウシアンの左半分のみをカーネルとして用いるよう改変
    kernel = kernel / kernel.sum()
    
    x_long = np.zeros(x.shape[0] + kernel.shape[0]-1)
    x_long[kernel.shape[0]-1:] = x
    x_long[:kernel.shape[0]] = x[0]
    x_GC = np.convolve(x_long,kernel,'valid')
    
    return x_GC

sigma_x = 10**(-2.5)
sigma_y = 10**(-2.5)
x_GC = LPF_GC(x,times,sigma_x)
y_GC = LPF_GC(y,times,sigma_y)

一次遅れ系

「ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)」記事より実装を拝借、改変。

def LPF_FO(x,times,f_FO=10):
    x_FO = np.zeros(x.shape[0])
    x_FO[0] = x[0]
    dt = times[1] -times[0]
    for i in range(times.shape[0]-1):
        x_FO[i+1] =  (1-  dt*f_FO) *x_FO[i]  + dt*f_FO* x[i]
    return x_FO

f0_x = 10**2
f0_y = 10**2
x_FO = LPF_FO(x,times,f0_x)
y_FO = LPF_FO(y,times,f0_y)

カルマンフィルタ

カルマンフィルタとしては、拝借したライブラリを用いた2通りの実装をおこなった。拝借したライブラリが行うフィルタリング処理の詳細については、Python で学ぶベイズフィルタとカルマンフィルタ (翻訳)の第 6 章 多変量カルマンフィルタを参照のこと（数式を省いた直感的な記述に溢れているため、数学的な素養が退化した素人にとって大変参考となる記事でした）。

状態空間モデルを定義しない実装

kf.Fを単位行列として定義してしまっていることを通じて、状態空間内での状態遷移を予測することを放棄している（ことを指して「状態空間モデルを定義しない」と表現した）。

ライブラリへのパラメーター引き渡しの趣旨は以下の通り。

• 状態（kf.x）は1つの要素のみを持つ配列として定義している。
  • この要素が「位置」（各時点における波形データの値）にあたる
• 状態方程式（kf.F）を単位行列として定義することを通じて、状態モデルの組み立て（状態空間内での状態遷移を予測すること）を放棄している
• 観測方程式（kf.H）として、状態空間における位置と、観測された位置（ノイズが乗った波における位置）を対応付けている
• 観測ノイズ（kf.R）としてはライブラリによる既定値をそのまま用いて、プロセスノイズ（kf.Q）のみをスカラー行列として定義することにより、フィルタの強さ（カルマンゲイン）を調整している。

from filterpy.kalman import KalmanFilter

def  LPF_KF1(x, Q):
    kf = KalmanFilter(dim_x=1, dim_z=1)
    kf.F = np.eye(1)
    kf.H = np.eye(1)
    kf.Q *= Q    kf.x[0] = x[0]
    (mu, _, _, _) = kf.batch_filter(x)
    x_KF = mu[:, 0]
    return x_KF

Q = 10**(-2)
x_KF1 = LPF_KF1(x, Q)
y_KF1 = LPF_KF1(y, Q)

状態空間モデルを定義した実装

こちらの実装においては、調和振動子に基づく状態空間モデルを定義した。ライブラリへのパラメーター引き渡しの趣旨は以下の通り。

• 状態（kf.x）は3つの要素を持つ配列として定義している。
  • ここで、配列内の1番目の要素が位置、2番目の要素が速度、3番目の要素が加速度にあたる
• 状態方程式（kf.F）により、運動方程式に基づく加速度、速度、および位置の間での関係をモデル化している
  • ここで、フィルタリング結果を正弦波にフィットさせることを狙って、運動方程式としては調和振動子のもの（位置、および角速度omegaに基づき加速度が決定し、その結果として速度、および位置の変化が生じる）を用いている
• 観測方程式（kf.H）として、状態空間における位置と、観測された位置（ノイズが乗った波における位置）を対応付けている
• 観測ノイズ（kf.R）としてはライブラリによる既定値をそのまま用いて、プロセスノイズ（kf.Q）のみをスカラー行列として定義することにより、フィルタの強さ（カルマンゲイン）を調整している。

from filterpy.kalman import KalmanFilter
omega = 2 * np.pi * f # 周波数fとして正弦波データの準備の際に定義したもの(f=5)を用いている

def  LPF_KF(x, Q):
    kf = KalmanFilter(dim_x=3, dim_z=1)
    kf.F = np.array([[1, dt, .5*dt**2],
                     [0., 1, dt],
                     [-(omega)**2, 0., 0.]])
    kf.H = np.array([[1., 0., 0.]])
    kf.Q *= Q
    kf.x[0] = x[0]
    (mu, _, _, _) = kf.batch_filter(x)
    x_KF = mu[:, 0]
    return x_KF

Q = 10**(-2)
x_KF = LPF_KF(x, Q)
y_KF = LPF_KF(y, Q)

各フィルタの適用結果とその評価

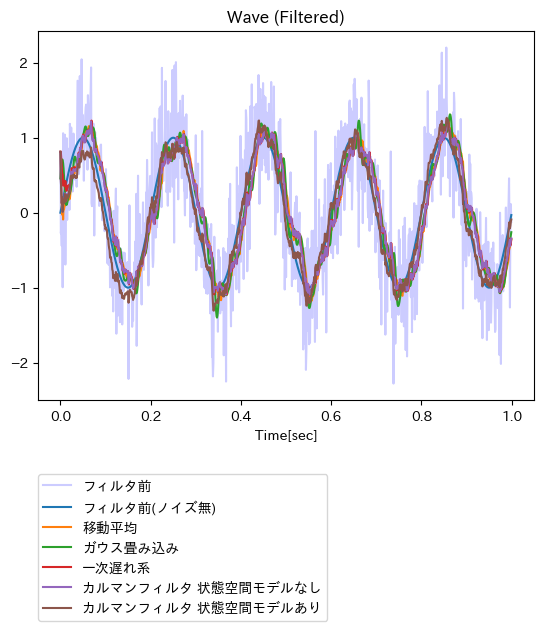
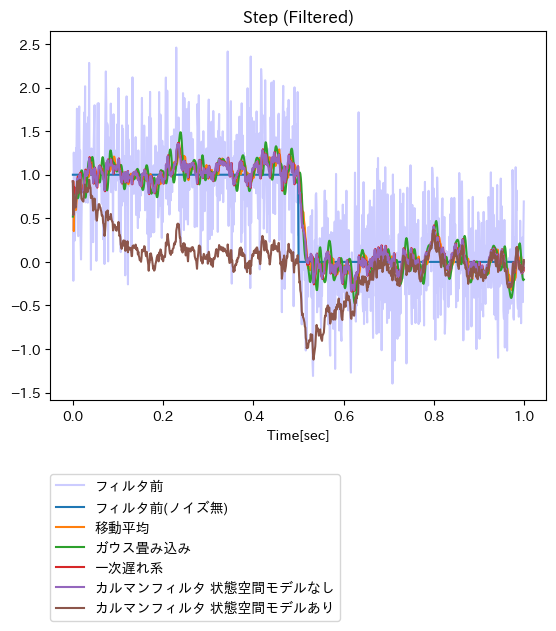
ともあれ、フィルタ適用対象とした元の時系列データ、および、各フィルタを適用した結果として得られた時系列データを重ねてプロットしてみる。

正弦波への適用結果

矩形波への適用結果

線が重なってしまっているので潰れて何がなんだかであるものの、パッと見た印象としては、調和振動子モデルに基づくカルマンフィルタ（茶色い線）を覗くと、それ以外の各フィルタによるノイズ除去性能（≒ノイズ無しオリジナル時系列データへの追従性）は大して変わらないように見受けられる。ともあれ、線が重なってしまって見づらい点を多少なりとも解消するために、各フィルタを適用した結果を一次遅れ系を基準とする形で比較してみる。

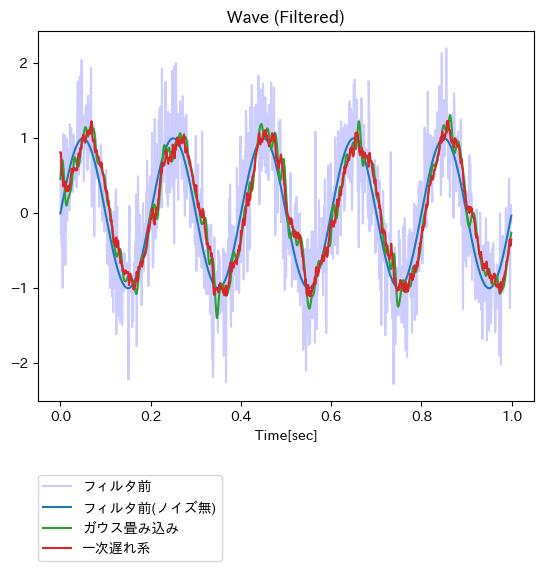
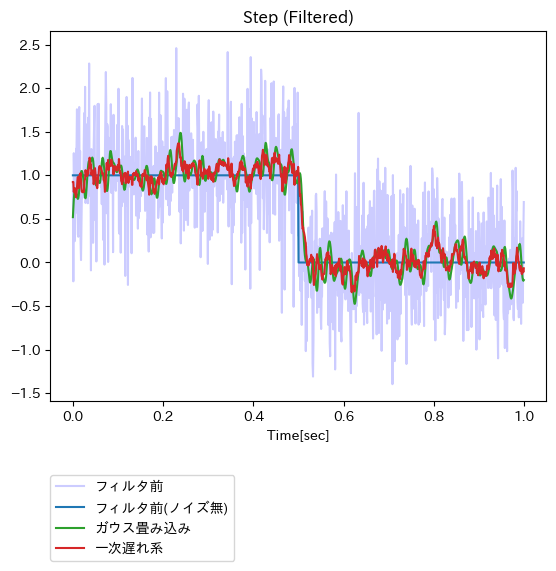
ガウス畳み込み vs 一次遅れ系

正弦波への適用結果（ガウス畳み込み、および一次遅れ系）

矩形波への適用結果（ガウス畳み込み、および一次遅れ系）

（好みの問題もあるかも知れないものの）ガウス畳み込みと比べて、一次遅れ系の方が上手くノイズを除去しているように感じらる。ただし、ガウス畳み込み処理での実装において、処理ロジックに対して我流で手を入れてしまっているため、それが不味かったのかも知れない。

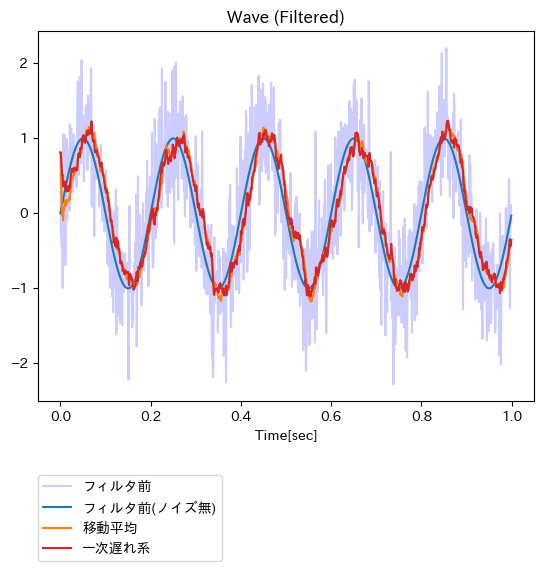
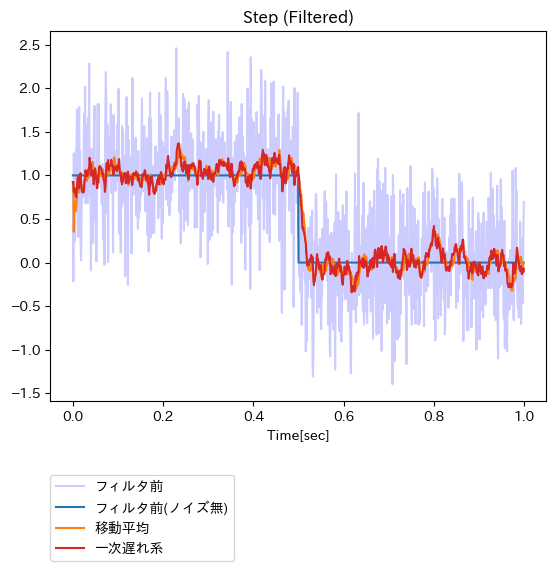
移動平均 vs カルマンフィルタ

では、お手軽度が非常に高い移動平均と一次遅れ系を比べてみるとどうか？

正弦波への適用結果（移動平均、および一次遅れ系）

矩形波への適用結果（移動平均、および一次遅れ系）

五十歩百歩というところか？とはいえ、フィルタ適用対象とした時系列における時間変動に対して、一次遅れ系の方がより敏感に追従しているようにも感じられる。一方で、非常にお手軽なフィルタである移動平均で事足りるならば、それで用を済ましてしまっても良い気もした。

一次遅れ系 vs カルマンフィルタ（状態空間モデルなし）

一次遅れ系とカルマンフィルタ（状態空間モデルなし）の比較を示す。

正弦波への適用結果（一次遅れ系、およびカルマンフィルタ（状態空間モデルなし））

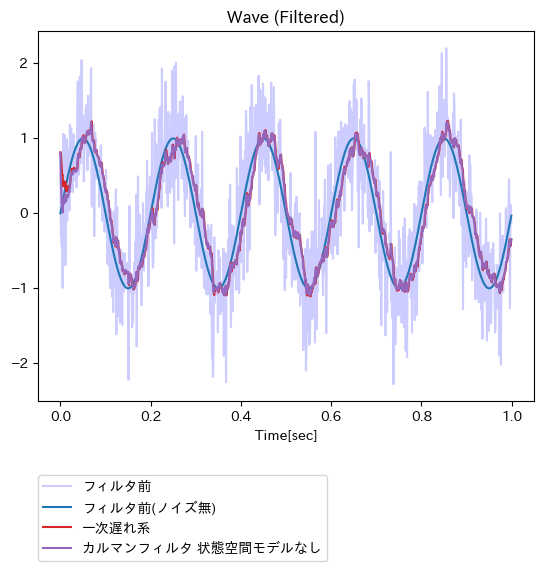
矩形波への適用結果（一次遅れ系、およびカルマンフィルタ（状態空間モデルなし））

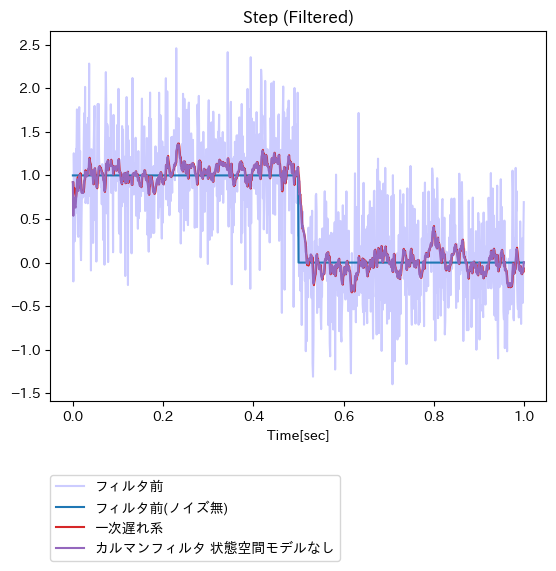
線ががっつり被っている様子を見て取ることが出来る。この結果について、状態空間モデルの組み立てを行わない（横着な）カルマンフィルタは一次遅れ系と本質的に同様であることを示すものであると直感的に理解してみた。

一次遅れ系 vs カルマンフィルタ（状態空間モデルあり）

最後に、一次遅れ系とカルマンフィルタ（状態空間モデルあり）の比較を示す。

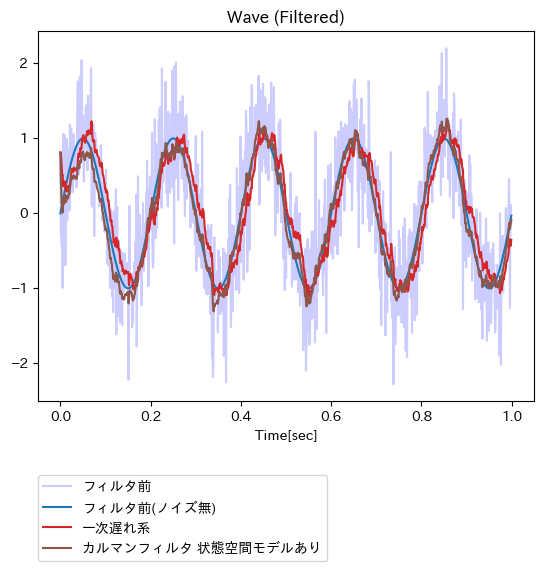
正弦波への適用結果（一次遅れ系、およびカルマンフィルタ（状態空間モデルあり））

矩形波への適用結果（一次遅れ系、およびカルマンフィルタ（状態空間モデルあり））

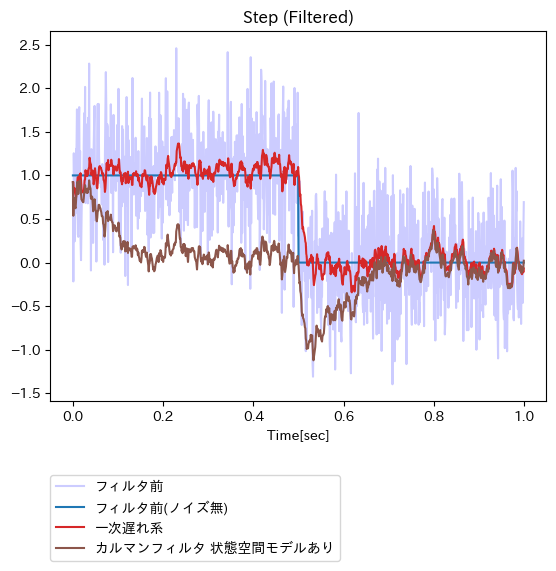
矩形波への適用結果が滅茶苦茶になってしまっている（矩形波と整合しない調和振動子モデルを利用している時点で、これは至極当然なはず）。一方で、正弦波への適用結果においては、フィルタ適用に伴う位相遅れが解消している点が注目に値する（一次遅れ系の赤い波はオリジナルの青い波より遅れている一方で、茶色い波はそうではない）。なお、~0.3sec頃までの時間範囲において、茶色い線と青い線の縦方向でのずれが大きい。これは、（過去方向から未来方向にフィルタリング処理を進めることに伴う）カルマンフィルタの収束が遅れていることに起因するように感じられた。

状態空間内で推定された速度の時間遷移

状態空間内で推定された加速度の時間遷移

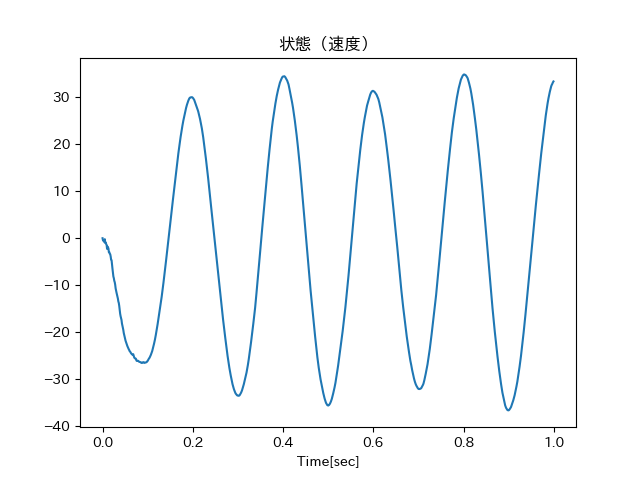
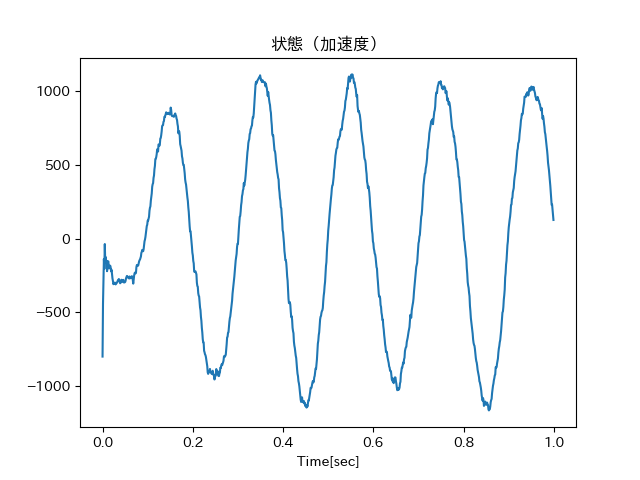
なお、kf.batch_filter(x)からの戻り値muには、状態空間内での速度、および加速度の推定結果が含まれている（それぞれmu[:, 1]、mu[:, 2]）。それらの推定結果を確認すると、それらしい推定がきちんと行われている様子を見て取ることが出来る。

感想

• 素人なりに初心者向けの時系列フィルタを実装して動かすことが出来た（気がする）。
• 「移動平均=イマイチ」という先入観があったものの、実際に動かしてみると（今回の要件の元では）そうでも無いという印象を受けた。
• ガウス畳み込みの結果が今ひとつだったのが残念（実装が不味かった可能性もあるが...）。
• 実態を反映しない状態空間モデルを用いたカルマンフィルタは悲惨な結果をもたらす。
• 適切な状態空間モデルを用いる（正弦波に対して調和振動子モデルを用いる）ことによって、フィルタリングに伴う位相遅れが解消した（ように見える）のが印象的だった。その理屈はピンと来ていないものの、状態空間モデルに基づくシステム状態遷移の推測が、システム状態変化の観測を通じた検知に先行していると想像してみた。