More than 1 year has passed since last update.

ローパスフィルタまとめ(移動平均法，周波数空間でのカットオフ，ガウス畳み込み，一時遅れ系)

Last updated at 2022-04-30Posted at 2020-10-27

最近，学生からローパスフィルタの質問を受けたので，簡単にまとめます．

はじめに

ローパスフィルタは，時系列データから高周波数のデータを除去する変換です．主に，ノイズの除去に使われます．

この記事では， A.移動平均法，B.周波数空間でのカットオフ，C.ガウス畳み込みとD.一次遅れ系の4つを紹介します．それぞれに特徴がありますが，一般のデータにはガウス畳み込みを，リアルタイム処理では一次遅れ系をおすすめします．

データの準備

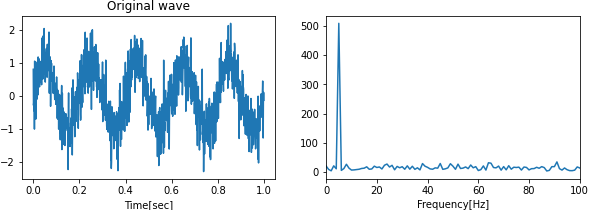
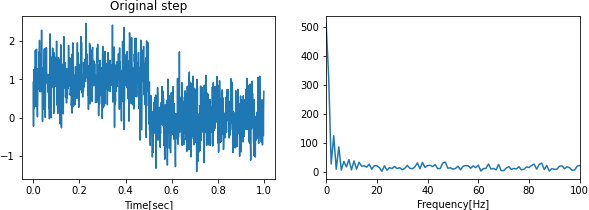
今回は，ノイズが乗ったサイン波と矩形波を用意して，ローパスフィルタの性能を確かめます．
白色雑音が乗っているため，高周波数成分の存在が確認できる．

import numpy as np
import matplotlib.pyplot as plt

dt = 0.001 #1stepの時間[sec]
times  =  np.arange(0,1,dt)
N = times.shape[0]

f  = 5  #サイン波の周波数[Hz]
sigma  = 0.5 #ノイズの分散

np.random.seed(1)
# サイン波
x_s =np.sin(2 * np.pi * times * f) 
x = x_s  +  sigma * np.random.randn(N)
# 矩形波
y_s =  np.zeros(times.shape[0])
y_s[:times.shape[0]//2] = 1
y = y_s  +  sigma * np.random.randn(N)

サイン波（左：時間, 右：フーリエ変換後):

矩形波（左：時間, 右：フーリエ変換後):

以下では，次の記法を用いる．
$x(t)$: ローパスフィルタ適用前の離散時系列データ
$X(\omega)$: ローパスフィルタ適用前の周波数データ
$y(t)$: ローパスフィルタ適用後の離散時系列データ
$Y(\omega)$: ローパスフィルタ適用後の周波数データ
$\Delta t$: 離散時系列データにおける，1ステップの時間[sec]

ローパスフィルタ適用前の離散時系列データを入力信号，ローパスフィルタ適用前の離散時系列データを出力信号と呼びます．

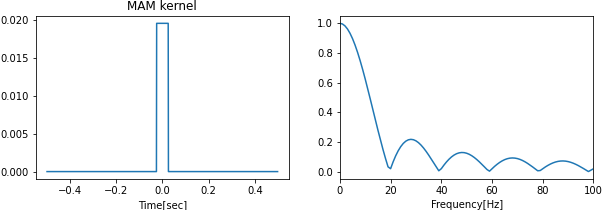
A.移動平均法

移動平均法(Moving Average Method)は近傍の$k$点を平均化した結果を出力する手法です．　

$$
y(t) = \frac{1}{k}\sum_{i=0}^{k-1}x(t-i)
$$

平均化する個数$k$が大きくなると，除去する高周波帯域が広くなります．

とても簡単に設計できる反面，性能はあまり良くありません．
また，高周波大域の信号が残っている特徴があります．

以下のプログラムでのパラメータ$\tau$は，
$$
\tau = k \cdot \Delta t
$$
と，時間方向に正規化しています．

def LPF_MAM(x,times,tau = 0.01):
    k = np.round(tau /(times[1] - times[0])).astype(int)
    x_mean =  np.zeros(x.shape)
    N = x.shape[0]
    for i in range(N):
        if  i-k//2 <0 :
            x_mean[i]  = x[: i - k//2 +k].mean()
        elif i - k//2 +k>=N:
            x_mean[i]  = x[i - k//2 :].mean()
        else :
            x_mean[i]  = x[i - k//2 : i - k//2 +k].mean()
    return x_mean

#tau = 0.035(sin wave), 0.051(step)
x_MAM = LPF_MAM(x,times,tau)

移動平均法を適用したサイン波（左：時間, 右：フーリエ変換後):

移動平均法を適用した矩形波（左：時間, 右：フーリエ変換後):

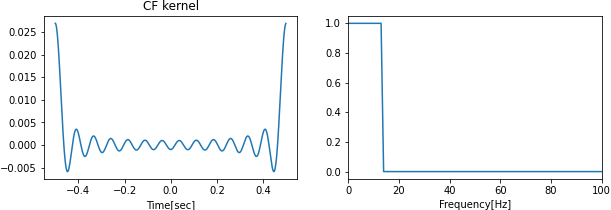
B. 周波数空間でのカットオフ

入力信号をフーリエ変換し，あるカット値$f_{\max}$を超える周波数帯信号を除去し，逆フーリエ変換でもとに戻す手法です．

\begin{align}
Y(\omega) = 
\begin{cases}
X(\omega),&\omega<= f_{\max}\\
0,&\omega > f_{\max}
\end{cases}
\end{align}

ここで，$f_{\max}$が小さくすると除去する高周波帯域が広くなります．
高速フーリエ変換とその逆変換を用いることによる計算時間の増加と，時間データの近傍点以外の影響が大きいという問題点があります．

def  LPF_CF(x,times,fmax):
    freq_X = np.fft.fftfreq(times.shape[0],times[1] - times[0])
    X_F = np.fft.fft(x)
    X_F[freq_X>fmax] = 0
    X_F[freq_X<-fmax] = 0
#     虚数は削除
    x_CF  = np.fft.ifft(X_F).real    
    return x_CF

#fmax = 5(sin wave), 13(step)
x_CF = LPF_CF(x,times,fmax)

周波数空間でカットオフしたサイン波（左：時間, 右：フーリエ変換後):

周波数空間でカットオフした矩形波（左：時間, 右：フーリエ変換後):

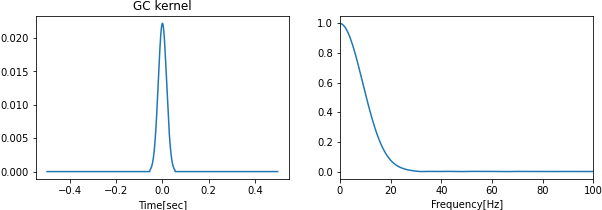
C. ガウス畳み込み

平均0, 分散$\sigma^2$のガウス関数を
$$
g_\sigma(t) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\Big(\frac{t^2}{2\sigma^2}\Big)
$$
とする．
このとき，ガウス畳込みによるローパスフィルターは以下のようになる．

$$
y(t) = (g_\sigma*x)(t) = \sum_{i=-n}^n g_\sigma(i)x(t+i)
$$

ガウス関数は分散に依存して減衰するため，以下のコードでは$n=3\sigma$としています．

分散$\sigma$が大きくすると，除去する高周波帯域が広くなります．

ガウス畳み込みによるローパスフィルターは，計算速度も遅くなく，近傍のデータのみで高周波信号をきれいに除去するため，おすすめです．

def  LPF_GC(x,times,sigma):
    sigma_k = sigma/(times[1]-times[0]) 
    kernel = np.zeros(int(round(3*sigma_k))*2+1)
    for i in range(kernel.shape[0]):
        kernel[i] =  1.0/np.sqrt(2*np.pi)/sigma_k * np.exp((i - round(3*sigma_k))**2/(- 2*sigma_k**2))
        
    kernel = kernel / kernel.sum()
    x_long = np.zeros(x.shape[0] + kernel.shape[0])
    x_long[kernel.shape[0]//2 :-kernel.shape[0]//2] = x
    x_long[:kernel.shape[0]//2 ] = x[0]
    x_long[-kernel.shape[0]//2 :] = x[-1]
        
    x_GC = np.convolve(x_long,kernel,'same')
    
    return x_GC[kernel.shape[0]//2 :-kernel.shape[0]//2]

#sigma = 0.011(sin wave), 0.018(step)
x_GC = LPF_GC(x,times,sigma)

ガウス畳み込みを行ったサイン波（左：時間, 右：フーリエ変換後):

ガウス畳み込みを行った矩形波（左：時間, 右：フーリエ変換後):

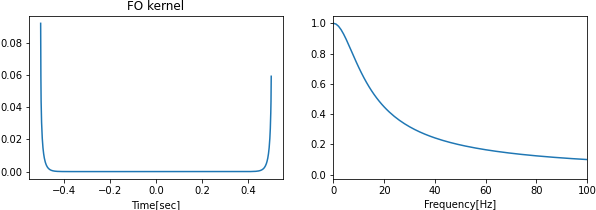
D. 一次遅れ系

一次遅れ系を用いたローパスフィルターは，リアルタイム処理を行うときに用いられています．
古典制御理論等で用いられています．

$f_0$をカットオフする周波数基準とすると，以下の離散方程式によって，ローパスフィルターが適用されます．

$$
y(t+1) = \Big(1 - \frac{\Delta t}{f_0}\Big)y(t) + \frac{\Delta t}{f_0}x(t)
$$

ここで，$f_{\max}$が小さくすると，除去する高周波帯域が広くなります．

リアルタイム性が強みですが，あまり性能がいいとは言えません．以下のコードはデータを一括に処理する関数となっていますが，実際にリアルタイムで利用する際は，上記の離散方程式をシステムに組み込んでください．

def LPF_FO(x,times,f_FO=10):
    x_FO = np.zeros(x.shape[0])
    x_FO[0] = x[0]
    dt = times[1] -times[0]
    for i in range(times.shape[0]-1):
        x_FO[i+1] =  (1-  dt*f_FO) *x_FO[i]  + dt*f_FO* x[i]
    return x_FO

#f0 = 0.011(sin wave), 0.018(step)
x_FO = LPF_FO(x,times,fO)